半空间的竖向冲击振动模拟与分析
奚亚男
(安徽工程勘察院,安徽 合肥 230011)
半空间的竖向冲击振动模拟与分析
奚亚男
(安徽工程勘察院,安徽 合肥 230011)
考虑在半无限空间边界上受到圆域分布脉冲作用的情况,可以用于探索人工地震及天然地震中地震波的特性及传播规律。为了简化讨论的难度,采用了半无限空间弹性体的假设模型,通过MATLAB编程实现,这也就是弹性动力学中的Lamb(兰姆)问题。
半空间模型;竖向冲击;地震波
0 引 言
在工程实践中经常使用强夯法加固地基、锤击法成桩施工、工程爆破等,他们的冲击作用对周围环境产生影响[1-2]。此外由公路和铁路运输,人类的其他活动引起的振动影响,这些问题都会造成灵敏仪器失灵,引起人的不适,并对附近建筑物造成危害。因此兰姆问题在工程中的运用及进一步的深入研究具有重要的意义[3-6]。在本文中采用半解析方法对半空间弹性体模型进行计算,其中运用到快速傅立叶变换等,对半解析解法的应用,大大简化了计算量和复杂性,并且适于向更复杂的工程实际进行推广,而这对于纯解析解法是无法想象的[7-11]。
为了易于接受,考虑按照定解问题的思路来解决该问题,即按照泛定方程、定解条件相结合的模式。所以本文从采用位移表述的纳维方程出发,运用势函数对其进行化简,得出简化形式的泛定方程,采用Laplace变换、傅里叶-贝塞尔积分等数学手段处理边界条件和初始条件,给出位移的解析形式解,最后采用数值积分的方法求出边界上各点不同时刻的位移值。
1 弹性动力学的位移表述
考虑半无限空间弹性体,结合平衡条件、变形相容条件和固体本构关系三方面,可以导出弹性动力学的位移表述,即纳维方程
(1)
(2)
2 泛定方程

(3)
本文所考虑的问题泛定方程可以导出
(4)
φ和χ叫做亥姆霍兹势。其中,c1,c2为速度常数。
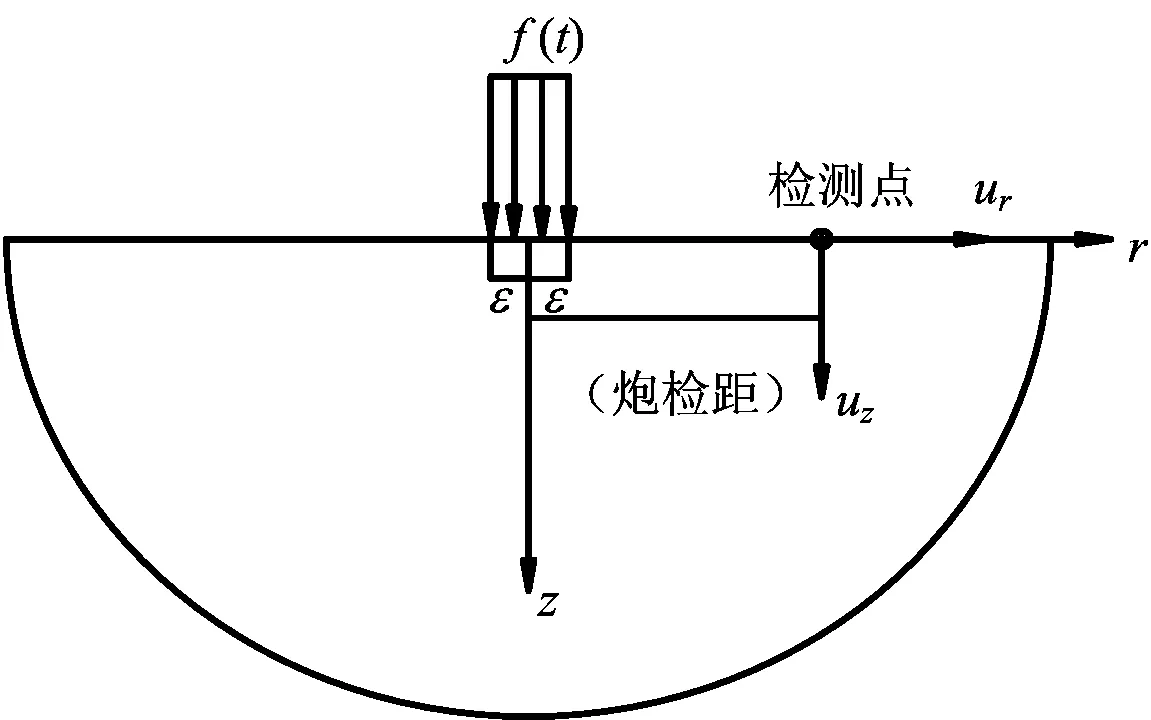
图1 半空间弹性介质模型
3 边值条件和初始条件的处理
在无限半空间的边界面z=0上,作用着以原点为圆心、以ε为半径的均匀脉冲力,脉冲力可用下式表示[2],即
(5)
处理后的边界条件可以表述为
(6)
(7)
考虑到撞击还未开始时,整个半无限空间都处于自然状态,相应的有下列初始条件:
(8)
4 采用数值解法求取边界面上的位移
为了避免繁杂的数学积分运算,考虑到工程实践的可行性,下面将采用MATLAB软件,运用数值解法来求取边界点处的位移值。可以选取几个特定的具有代表性的点,给出其在各时刻的位移值,这在工程实践和理论研究中都具有重要的价值。
为了显示震动的传播过程,特选取地基表面三个不同的位置,炮检距分别为D=5 m,D=10 m,D=15 m。
在各向同性弹性土半空间中,由某一扰动所产生的波场可由压缩波、剪切波及瑞利波描述,其中压缩波和剪切波在介质内部传播,故称其为体波,瑞利波主要在弹性半空间表面传播,故称其为面波。各向同性弹性介质中压缩波和剪切波速度与介质Lame常数有如下关系:
(9)
(10)
其中,G、λ为Lame常数,ρ为密度,cs,cp为横波波速和纵波波速。
图2~4所示为不同炮检距时的位移随时间变化图。对比图2~4可以看到随着观测点距离的增大,直达波到达的时间推迟,符合实际。当面波到达时位移值达到最大,说明面波对质点位移造成很大的影响。

图2 炮检距D=5 m时位移

图3 炮检距D=10 m时位移

图4 炮检距D=15 m时位移
当改变激振半径ε=0.5 m时,D=15 m,得到的位移值如图5所示。
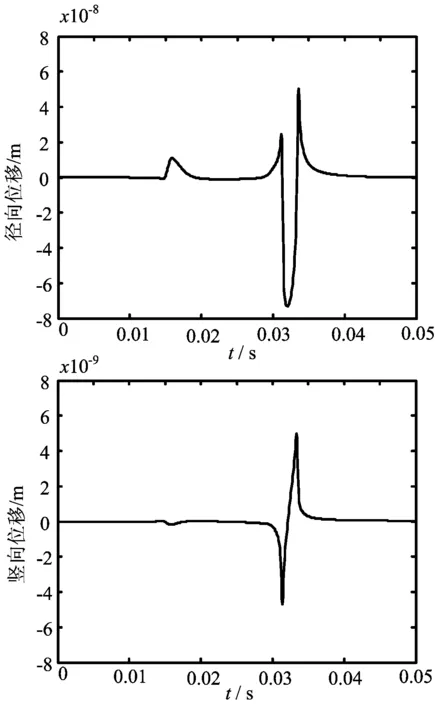
图5 激振半径ε=0.5 m时的径向位移
可以发现当半径增大时,位移值变小,位移峰值宽度变大,这主要因为,在激振力确定时,半径变大导致激振应力减小,从而位移会相应减小。
改变激振力的持时为原来的10倍即t0=5×10-3s,D=15 m处位移如图6所示。
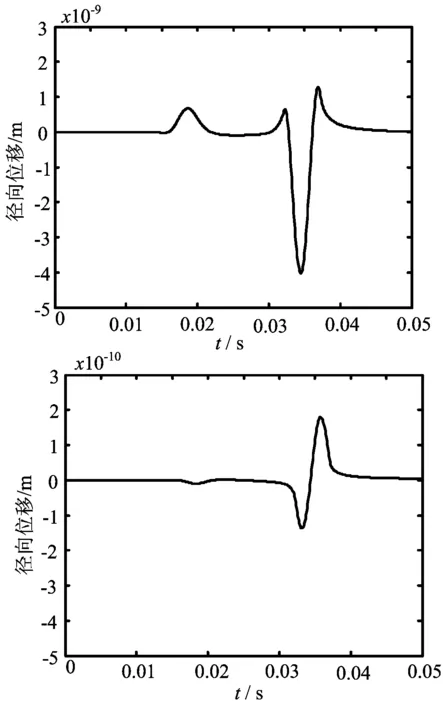
图6 激振力持续时间t0=5×10-3s时的径向位移
可以看出改变激振力持续时间时,由于激振冲量固定,激振力时间越长,激振力的幅值越小,导致位移的幅值变小,峰值宽度变大。
根据本文所提出的半解析方法,探讨了不同激振力因素对表面各点位移的影响。对于半无限空间模型求得了地基表面各点的振动位移图像。
对于半无限空间情形,各点位移变化的总体图像是:地基表面各点的径向位移及竖向位移都依时间顺序先后出现三个极值,其幅度也有所不同。
(1) 据已有的地震波传递的资料,可以清晰地判定出第一个极值对应着纵波,也可称为压缩波、体波,代表着地基各微元体的体积变化,纵波的波速快,但是相对的震动幅度小很多,所以第一个极值的数值相对较小。
第二个极值对应着横波,也可称为剪切波,代表着地基各微元体的形状变化,而横波的波速相比纵波有一定的差距,所以图像上可以看到第二个极值的出现较第一个极值的出现要推迟相当一段时间,其时间差正是波速的相差所导致的。
第三个极值对应着面波,也就是通常所说的瑞利波,这是在地震波传递过程中发生相互作用但是只存在于地基表面的地震波形式,对于其产生的详细分析可以从任何一本介绍地震波的著作中找到,本文在此就不做过多的叙述。在本文的论述中清楚地展现了在地震中地表产生了三种不同性质的波动形式,以及其传播的速度、震动幅度都有所不同。
(2) 对比各极值点的幅值可以发现,第三个极值的振动幅度最大,这说明当发生地震时,横波和面波的破坏作用最大,而纵波虽然传播的速度最快,但是由于其震动幅度相对较小,一般难以觉察,然而这对地震的监测有着很重要的意义,可以在监测到纵波时及时采取措施将破坏程度降到最低。
(3) 考虑地表振动幅度随炮检距的影响。可以看出,随着距震源距离的逐渐增大,三个极值出现的时间推迟,各极值之间的时间间隔增大,更容易清晰地看到三个波极值的出现。
(4) 改变激振半径时,激振半径越大位移幅值越小,得到的位移曲线变化越缓,极值的持续时间越长。
(5) 改变激振力持续时间时,由于激振冲量固定,激振力时间越长,激振力的幅值越小。这就导致位移的幅值变小,且峰值宽度变大。
5 结束语
对于本文所提出的半解析方法,在理论和工程实践上都有重要的意义,但是也存在着一些无法避免的问题,即为了讨论的方便和减小问题的难度,对于半无限空间考虑的对象是均匀土层,而任何工程实践的地基土都是极端复杂的,充满着各种由非均匀介质因素导致的非线性问题,具体的更细化的研究有待于进一步深入的讨论。
[1] Lamb H. On the propagation of tremors over the surface of an elastic solid [J]. Philosophical Transactions of the Royal Society (London). 1904(A203):1~42.
[2] Pekeris C L. The seismic buried pulse [J]. Proceedings of the National Academy of Sciences,1955(41):629~639.
[3] 钟 阳,王哲人,郭大智.求解多层弹性半空间轴对称问题的传递矩阵法[J].土木工程学报,1992,25(6):37~43.
[4] 陆明万,罗学富.弹性理论基础[M].北京:清华大学出版社,2001.
[5] 梁昆淼.数学物理方法[M].北京:人民教育出版社,1986.
[6] 刘广裕,刘凯欣.区域脉冲载荷下二维Lamb问题的精确求解[J].固体力学学报,2007,28(4):341~346.
[7] 柯宅邦.基桩低应变动测空间轴对称问题的理论与实践研究[D].合肥:合肥工业大学,2006.
[8] 段 军.基桩低应变动测空间三维问题的理论研究[D]. 合肥:合肥工业大学,2008.
[9] 刘东甲.纵向振动桩侧壁切应力频率域解及其应用[J],岩土工程学报,2001,23(5):544~546.
[10] 刘东甲,刘煜洲,王杰英.单缺陷桩反射波法动测曲线峰-峰点反演的精度研究[J].岩石力学与工程学报,2003,22(8):1383~1389.
[11] 刘东甲,王建国.均匀土中有限长桩瞬态横向动力响应[J].工程力学,2003,20(6):160~165.
2016-06-08;修改日期:2016-06-16
奚亚男(1984-),女,江苏启东人,硕士,安徽工程勘察院工程师.
P315.31;TU973.31
A
1673-5781(2016)04-0439-04

