海底隧道地震动力响应研究
刘天添, 戚承志, 陈昊祥, 杨谨瑞
(北京建筑大学 土木与交通工程学院 北京市高校工程结构与新材料工程研究中心, 北京 100044)
海底隧道地震动力响应研究
刘天添,戚承志,陈昊祥,杨谨瑞
(北京建筑大学 土木与交通工程学院 北京市高校工程结构与新材料工程研究中心, 北京100044)
摘要:高水压作用下海底隧道的地震动力响应是一个需要深入研究的问题. 基于Winkler地基模型,利用动力平衡条件和微分关系推导出了仅由弯曲引起的梁振动方程,利用分离变量法求得了海底隧道的振型和自振频率,并推导出了地震作用下海底隧道与地基之间的动力相互作用系数以及隧道结构位移表达式. 通过算例计算研究了水压对于结构的自振频率、结构位移以及相互作用系数的影响. 研究表明,高水压作用下结构的地震动力响应不可忽略.
关键词:海底隧道; 水压力; Winkler地基模型; 自振频率; 振动位移
目前的跨海交通主要有桥梁和隧道两种形式.也有桥隧并举的形式. 而海底隧道因对海洋环境及水上航运影响小、受恶劣气候及战时破坏影响小等优点,在近年来跨海交通的不同方案比选过程中越来越显现其优越性,并日益成为城市、地区、甚至国家之间的重要连接手段和交通命脉. 但是相较一般的陆上隧道,海底隧道又有自己的难点. 如海底隧道深埋于地下,深水海底地质勘察比地面地质勘察难度更高、投入更大,不仅影响勘察的准确性,而且漏勘和失真情况的风险也会相应增加;海底隧道周边围岩裂隙中一般会有较高的孔隙水压力和渗水压力,会造成岩体弱化,使围岩的有效应力和成拱能力降低,进而影响地层的稳定性;隧道绝大部分位于海床之下,衬砌需要承受长期的高水压作用;在穿越断层构造及地震破碎带时需要高度关注地震作用对隧道安全性的影响等. 这些难点的存在使得海底隧道从设计、施工到运营维护等一系列过程都比一般隧道更加复杂,同时也推进着海底隧道的研究.
在抗震研究早期,人们认为地下构造物因受到围岩的约束和限制,在地震时随着地基的运动而运动,地震对地下构造物的破坏影响相比地表破坏小得多,可以不用考虑. 根据统计,过去地震中很少有地下隧道结构遭受地震破坏似乎也验证了这一点. 然而在1995年日本阪神大地震中,神户市区间隧道和地铁车站等大型地下结构均遭受了重大破坏. 这一事实迫使人们重新审视地下结构物的破坏,并开始怀疑传统的地下结构抗震理念,自此地下结构抗震研究的热潮逐渐兴起. 目前国内外对地下结构的抗震研究大多集中在地铁车站和山岭陆地隧道,而对水压力影响下海底隧道衬砌结构动力响应的研究则相对较少.
总的来说,由于海底隧道建造在海底,属于一种特殊的地下结构,且它处于非常复杂的工程地质和水文地质环境中,存在很多诸如断裂构造、破碎带等不确定因素,建成后难以更改,一旦发生地震破坏,其后果是难以估量的. 因此,对海底隧道地震时的动力响应进行研究就显得尤为重要. 对于传统陆上地下线型隧道结构,在研究轴向传播的地震动作用下垂直于轴线的横向振动时,一般只研究了轴力、内外阻尼、转动惯性、横截面剪切变形等一种或几种因素的影响. 而对于海底隧道这种线型结构所受到的高水压力对结构横向振动的影响研究,主要是通过一些有限元软件进行数值模拟,目前还缺乏系统的理论研究,高水压对于隧道结构的地震响应的影响还不清楚. 鉴于此,本文将基于土与结构的相互作用,结合结构动力学和弹性力学相关知识,研究高水压对于结构自振频率及横向振动位移的影响. 首先是利用平衡条件和微分关系推导出仅由弯曲引起的结构自由振动方程和强迫振动方程. 之后利用分离变量法和输入地震振动形式分别求得了含水压影响的结构自振频率和结构振动位移的表达式,并结合算例研究了地震作用下水压对海底隧道结构自振频率和振动位移的影响.
1振动方程
1.1模型选取
温克尔(Winkler,1867)地基梁模型(见图1)由捷克工程师温克尔(Winker)提出,是—种常用的线弹性地基模型. 它的基本假设是土介质表面任一点竖向位移w=w(x,t)与该点所受的地基反力p(x,t)成正比,而与其他点地基反力无关,其表达式如下:
p(x,t)=k0w(x,t)
(1)
隧道为线型结构,重点研究沿结构长度方向的结构振动和受力情况,故将式(1)中的单位面积上地基基床系数k0变换为单位长度上的地基基床系数k. 利用关系式k=k0b,则(1)式变为:
p(x,t)=kw(x,t)
(2)
温克尔模型简单且为线性,在地下结构的设计和分析中,常选用此模型来模拟土与结构的相互作用.
1.2水压下的轴力
目前,海底隧道水压力取值通常采用折减系数法、全水头法、可能最大水头值法3种估算方法. 这3种方法应用最广泛的是折减系数法,而数值计算法和解析法有时也有应用. 本文在考虑高水压影响时,采用全水头法计算水压力,并将水压力按照静水压力考虑. 对于海底隧道来说,水压力是突出问题,它不仅影响隧道结构的横向受力,还会引起隧道结构纵向轴力变化,而隧道是一个线型结构,两端可以看作铰结在地基上,故可以将其按照平面应变问题进行考虑. 假设水压力用qw表示,则根据弹性力学知识:
(3)
根据广义胡克定律由εz=0可得:
(4)
则水压力引起的轴力可按下式近似求得:
(5)
若设衬砌结构所受初始轴压为N0,则结构轴向所受总压力(以压力为正)为:
N=N0+Nw=N0+2υπb2qw
(6)
式中,σr、σθ、σz分别为衬砌结构径向、环向、轴向的应力,a、b分别为衬砌结构的内半径和外半径.
1.3振动方程推导
本文在建立梁横向振动方程时作了如下几点假设:
1)选用线弹性温克尔地基梁模型;
2)不考虑错缝拼装和螺栓连接效应的影响,结构按等刚度原则考虑;
3)对于浅埋结构,一般认为埋深越大,结构受到围岩的约束就越强,结构的动力响应越小,本文在推导过程中不考虑埋深对结构动力响应的这种影响;
4)不考虑梁在运动过程中剪切变形和转动惯量的影响,即认为梁挠曲线的斜率仅由弯矩所引起;
5)忽略阻尼影响.
设有如图2所示的地铁隧道简化模型,沿轴向x方向的抗弯刚度为EI,单位长度质量为m(x)=ρA,作用在模型上的横向荷载包括地基反力和惯性力,模型横向位移用w(x,t)表示.
如图3所示,取梁上任一截面x处的微段dx为隔离体,结构轴线在弯矩作用下将会发生弯曲,微段右端面与左端面之间存在一个微小的倾斜角度dφ=dx∂2w/∂x2. 因为∂2w/∂x2=∂θ/∂x,则有dφ=dx∂2w/∂x2=dx∂θ/∂x(θ为弯矩产生的挠曲线斜率). 该微段上除了作用在两个截面上的弯矩M、剪力Q、轴力N和地基反力p(x,t)外,根据达朗贝尔原理,还有假设的惯性力fI(x).
根据竖向力的平衡则有:
(7)
即
(8)
由于不考虑梁在运动过程中剪切变形和转动惯量的影响,梁挠曲线的斜率仅由弯矩造成. 根据微分关系有:
(9)
将式(9)代入式(8)得考虑轴力影响的梁自由振动方程:
(10)
将式(2)、式(6)代入上式即可得到考虑高水压影响的梁自由振动方程:
(11)
式中:E——衬砌结构的弹性模量(N/m2);
Iz——衬砌结构的横截面惯性矩(m4);
υ——衬砌结构的泊松比.
事实上,已有文献推导了考虑包括轴力、剪切变形、内外阻尼、横截面转动惯性以及地基参数等因素的更为一般的梁振动方程,本文只研究包含水压力影响的仅由弯矩引起的比较简单的情况.
若梁作强迫振动时,wg(x,t)为自由场地基侧向位移,则文克尔地基表达式变为:
p(x,t)=k[w(x,t)-wg(x,t)]
(12)
此时梁强迫振动方程变为:
(13)
2振动方程的求解
2.1自振频率的求解
为求解式(11)表示的梁自由振动方程的振型和自振频率,本文采用分离变量法,假设解具有如下形式:
w(x,t)=W(x)T(t)
(14)
代入式(11)整理得:
(15)
式(15)等号两端分别是x和t的函数,对于任意独立的x和t,式(15)只能等于一个常数,此常数用λ4表示. 则有:
(16)
(17)
式(16)为常见的无阻尼单自由度振动方程,其解为:
T(t)=Acosωt+Bsinωt=asin(ωt+φ)

W(x)=C1cosαx+C2sinαx+C3coshβx+C4sinhβx
(19)
利用边界条件:
W(0)=W″(0)=0W(L)=W″(L)=0
可得振型函数的解为 :
(20)

(21)
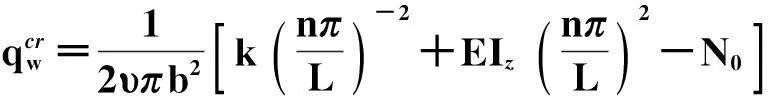
2.2强迫振动方程的求解
对于方程(13),其解包括两部分如下:
w(x,t)=wc(x,t)+wp(x,t)
(22)
式中,右边第一项代表自由振动解,反映了初始条件对结构体系振动的作用;第二项代表强迫振动特解,表示外来输入对结构体系振动的作用. 因为阻尼作用影响总是存在,第一项在一段时间之后将很快衰退而消失,可以不用考虑,只剩下一个稳定的纯强迫振动(常称为稳态振动),其振动特性由外界干扰力的性质以及变化规律决定.
强迫振动方程在求解时常作如下假定:地下结构和地基土是各向同性、均匀的线弹性介质;不考虑地震波输入时的随机性和复杂性,地震波按剪切波考虑,入射方向与隧道轴向之间夹角为零.
如图4所示,假定自由场土介质某一时刻的侧向位移为wg(x,t),幅值为D. 隧道结构侧向位移用w(x,t)表示,它与自由场土介质对应时刻侧向位移形状相似而幅值不同,两者相差一个相互作用系数R.
地震波以简谐波形式在地层中传播,地层在地震波作用下发生简谐位移,其位移数学表达式假定如下:
地震位移场:
wg(x,t)=Dsin(γx-θt)
(23)
结构的振动位移:
w(x,t)=RDsin(γx-ωt)
(24)
式中:θ——地震波频率;
ω——结构振动频率;
λ——地震波波长.
为了求出结构振动位移,应首先求出相互作用系数R. 将式(23)和(24)带入式(13)得:
[EIγ4-(N0+2υπb2qw)γ2+k-ρAω2]RDsin(γx-
ωt)=kDsin(γx-θt)
(25)
整理可以得到相互作用系数为:
(26)
把式(26)带入式(24)可以得到结构振动位移表达式为:
(27)
将式(24)和式(27)进行比较容易看出,外荷载频率与结构振动频率相等,即θ=ω,则相互作用系数表达式为:
(28)
把式(28)带入式(24),得到结构振动位移表达式如下:
(29)
3算例
某盾构圆形海底隧道,最低点位于水面下130m,水压约1.3MPa,隧道长度L=200m,属大盾构,外径d1=16.7m,内径d2=15.7m,混凝土衬砌密度ρ=2 600kg/m3,弹性模量E=3.0×104MPa,泊松比υ=0.3,初始轴向压力N0=50 000kN,取地基基床系数k0=2.0×107N/m3. 地震强度PGV=0.3m/s(相当于8度地震),地震位移幅值D=2.9cm,地震波长λ=100m,波速v=180m/s,频率θ=11.31rad/s,地震动位移函数为wg=0.029×sin(0.062 8x-11.31t).
为了考察水压对结构自振频率的影响,结构单位长度质量、抗弯刚度、地震动频率均保持不变,根据式(21)可得到不考虑水压影响和考虑水压为2MPa影响的结构前10阶的自振频率以及不同水压下结构前三阶的自振频率,具体计算结果如图5和图6所示.
从图5可以看出,水压对结构低阶自振频率与高阶自振频率的影响差别很大. 考虑2 MPa水压时,前五阶自振频率下降幅度为5.99%~61.56%,六阶自振频率以后下降幅度在3.38%以下. 因此,水压对结构低阶频率影响较大,对结构的高阶频率影响几乎可以忽略. 根据图6可以看出,结构的前三阶的自振频率随着水压的逐渐增大而近似线性减小. 并且从图中可以看出,水压增大到一定值后,结构的自振频率为0,此时结构不振动,这也说明了水压对结构有一定的限制作用,阻碍着结构的振动. 但从图5中可以看出,结构的自振频率为0时,所受临界水压须达到2.5 MPa以上,目前修建的海底隧道所受水压最高在2 MPa左右,因此不会出现自振频率为0的情况.
在研究水压对衬砌结构振动位移的影响时,为使研究具有针对性,取结构振动位移最大的时刻的位移幅值进行研究. 图7和图8分别给出了不同水压力下,结构振动位移幅值及地基与结构相互作用系数的变化情况. 从图7中可以看出,结构的振动位移幅值随着水压的增大而逐渐增大. 这可能是因为随着水压力逐渐增大时,隧道结构的自振频率会减小,表现为结构刚度逐渐降低,从而使结构的振动位移幅值增大. 从本例的计算结果可以看出,水压对结构振动位移幅值的变化已超过8%,水压力对结构振动位移幅值的影响不可忽略. 从图8中可以看出,水压对相互作用系数的影响也很显著. 随着水压的逐渐增大,相互作用系数也在逐渐增大. 这说明由于水压的存在,地震动对结构的动力响应的影响将加强,这也验证了前述水压对结构振动位移幅值的增大效应.
4结论
本文采用温克尔地基模型,结合结构动力学和弹性力学相关知识推导了仅由弯曲引起的梁自由振动方程和强迫振动方程,并求出了含高水压影响的结构的自振频率表达式以及结构的位移表达式. 通过算例得出水压对结构的低阶自振频率影响显著,对高阶自振频率的影响可以忽略,并且结构的位移
幅值随水压增大而增大. 因此,对处于高水压情况下的隧道来说,水压影响应该考虑.
参考文献:
[1]谭忠盛,王梦恕,罗时祥.琼州海峡铁路隧道方案初步比选分析[J].中国工程学,2009,11(7):39-44
[2]石新栋,皇甫明,谭忠盛,等.跨琼州海峡隧道方案的探讨[J].隧道建设,2010,30(6):625-628
[3]Dowing C H, Rozen A. Damage to rock tunnels from earthquake shaking[J]. Journal of the Geotechnical Engineering Division, 1978, 104(2):175-191
[4]张维. 日本兵库县南部地震灾区现场震害考察[J].工程抗震, 1995(1):2
[5]杨光,沈繁銮.日本阪神地震灾害的一些调查统计数据[J].华南地震, 2005, 25(1):83-86
[6]Stephen N G.The second spectrum of Timoshenko beam theory—further assessment[J].Journal of Sound and Vibration, 2006, 292(1-2) :372-389
[7]Majkut L. Free and forced vibrations of Timoshenko beams described by single difference equation[J]. Journal of Theoretical and Applied Mechanics, 2009,47(1): 193-210
[8]Bogacz R, Czyczula W. Response of beam on visco-elastic foundation to moving distributed load[J]. Journal of Theoretical and Applied Mechanics, 2008, 46(4): 763-775
[9]徐英乾,戚承志,沙曼.阻尼对地下区间隧道动力响应的影响[J].岩土力学, 2012(2):196-200
[10]铁摩辛柯,古地尔.徐芝纶译.弹性理论[M].北京:人民教育出版社,1964:12
[11]戚承志, 陈灿寿, 陈国兴, 等. 地基弹性参数对于长型大截面地下结构横向自由振动的影响[J]. 防灾减灾工程学报, 2011(6): 622-626
[12]陈灿寿,戚承志,陈剑杰,等.长型大截面地下结构的横向自由振动方程[J].世界地震工程, 2011, 27(1): 90-95
[13]韦洪刚, 杨秀仁,戚承志,等. 地下结构纵向地震响应分析[A]∥全国第一届防灾减灾工程学术研讨会[C], 2011
[14]韦洪刚,杨秀仁,戚承志. 长型地下结构在地震作用下的横向响应分析 [D].北京:北京建筑大学, 2012
[15]彭俊生,罗永坤,彭地.结构动力学、抗震计算与SAP2000应用[M].成都:西南交通大学出版社,2006:90-97
[责任编辑:佟启巾]
Research on Seismic Dynamic Response of Submarine Tunnel
Liu Tiantian,Qi Chengzhi,Chen Haoxiang,Yang Jinrui
(School of Civil and Traffic Engineering, Beijing Higher Institution Engineering Research Center of Structure and New Materials,Beijing University of Civil Engineering and Architecture, Beijing 100044)
Abstract:Seismic dynamic response of submarine tunnel under high water pressure is a problem in need of further investigation. Based on Winkler’s foundation model, the structure vibration equation with consideration of only bending is derived by using dynamic equilibrium condition and differential relations. Using the method of variable separation, the vibration mode and natural vibration frequencies of submarine tunnel are obtained. And the interaction coefficient between submarine tunnel and foundation and structural displacement is also determined. Numerical example is given and the effect of water pressure on structural natural vibration frequencies and structural displacement and interaction coefficient is studied. Investigation shows that structural seismic dynamic response under effect of high water pressure should not be neglected.
Key words:submarine tunnel; water pressure; Winkler foundation model; natural frequency; vibration displacement
中图分类号:U459.9; TU435
文献标志码:A
作者简介:刘天添(1988—),男,硕士研究生,研究方向:结构抗震、岩土力学.
基金项目:国家自然科学基金项目(51174012,51478027);北京市属高等学校创新团队建设与教师职业发展计划项目(IDHT20130512);国家重点基础研究发展计划(973)项目(2015CB0578005)
收稿日期:2015-09-06
文章编号:1004-6011(2016)01-0046-06

