兰州市财政收入与GDP的协整分析与误差修正模型研究
王玉芳


摘要:利用协整理论对兰州市1978-2013年的财政收入和GDP的关系进行实证分析,结果表明,兰州市财政收入和GDP相关度较高,整体上存在长期稳定的协整关系,二者的动态调整机制可自动实现长期均衡;Granger因果检验表明,财政收入和GDP间存在单向因果关系,即GDP的增长是兰州市财政收入增长的决定因素。
关键词:协整分析;Granger因果检验;误差修正模型
中图分类号:F127 文献识别码:A 文章编号:1001-828X(2016)009-000-02
一、引言
作为实现政府职能和协调收入分配的重要保障,财政收入通常包括地方财政收入和中央财政收入,是衡量一个地区或国家的财力和经济发展水平的重要指标[1]。国内生产总值(GDP)是一个地区或国家在一定时期内国民经济活动最终成果的总量指标,反映经济发展的综合水平。财政收入的影响因素主要有经济发展水平、收入分配政策和物价水平。本文以兰州市为例,重点研究财政收入与GDP即经济发展水平间的关系。
目前,国内学者对GDP和财政收入关系的研究主要集中在增长速度的比较和二者关系的探究。何凌云等(2013)[2]对财政收入增速超过经济增长增速的问题进行了统计分析;林国立等(2015)[3]基于GDP与财政收入间的关系,对蚌埠市财政收入和GDP增幅的差异性进行分析。王玉华等(2009)[4]对山东省财政收入和GDP进行时间序列分析,认为二者存在长期稳定关系;文秀琴(2013)[5]对河南省财政收入和GDP进行相关分析,证明二者存在一元线性回归关系。本文采用协整理论,深入分析兰州市财政收入和GDP间的关系,并建立误差修正模型。
二、研究方法
(一)单位根检验
单位根检验主要用于检验变量的平稳性并推断其单整阶数,常用的方法包括ADF检验、DF检验和PP检验。本文采用使用最广泛的ADF检验,其原理是将因变量的滞后差分项加入回归方程以控制高阶序列相关,基本模型为:
式中,xt为时间序列,t为时间趋势因素,Δ为一阶差分,n为最佳滞后阶数,为白噪声。原假设:H0: λ=1,即{xt}有一个单位根(非平稳)。本文采用AIC准则确定最佳滞后阶数n,并使用Mackinnon临界值判定序列的平稳性。
(二)协整检验
协整检验用于确定变量间是否存在长期稳定的均衡关系,主要方法包括Engle-Granger两步法和Johansen检验法。Engle-Granger两步法适用于两变量的协整分析,而Johansen检验法常用于多变量的协整分析,且可求出变量间可能存在的多种协整关系。因财政收入和GDP仅为两变量,故本文采用Engle-Granger两步法。设有一阶单整变量{yt}与{xt},首先对其进行协整回归:
其次,检验残差的平稳性,若平稳,则可认为{yt}和{xt}间存在(1,1)阶协整关系,即存在长期均衡,反之不存在。在存在协整关系的基础上,引入误差项建立误差修正模型:
ecmt为误差修正项。误差修正模型既可描述变量的长期波动,又可通过差分项描述变量的短期波动,故该模型可研究变量的静态(长期)趋势和动态(短期)特征。
(三)Granger因果关系检验
即使判定两变量间存在长期均衡关系,但是否存在因果关系,还需进一步检验。若变量x有助于预测y,即对y回归时,加上x的滞后值可显著提高回归的解释能力,则称x为y的Granger原因,否则为非Granger原因。若x为y的Granger原因,说明x中包括了预测y的有效信息。其模型如下:
检验的零假设H0: a1=a2=…=aq=0,即x是y的非Granger原因。若零假设成立,则有:
用最小二乘法求出式(4)和式(5)的残差平方和SSE1和SSE0,构造自由度为(q,T-p-q-1)且服从F分布的统计量。其中,S为样本容量,p为y的滞后阶数,q为x的滞后阶数,p和q用AIC准则确定。比较F统计量与临界值的大小,若F大于临界值,则拒绝零假设,即x为y的Granger原因,反之接受零假设。
三、实证研究
(一)样本数据选择和数据处理
本文以兰州市为例,以1978-2013年财政收入(CZSR)和地区生产总值(GDP)为样本数据,所有数据均来源于《兰州市统计年鉴》。
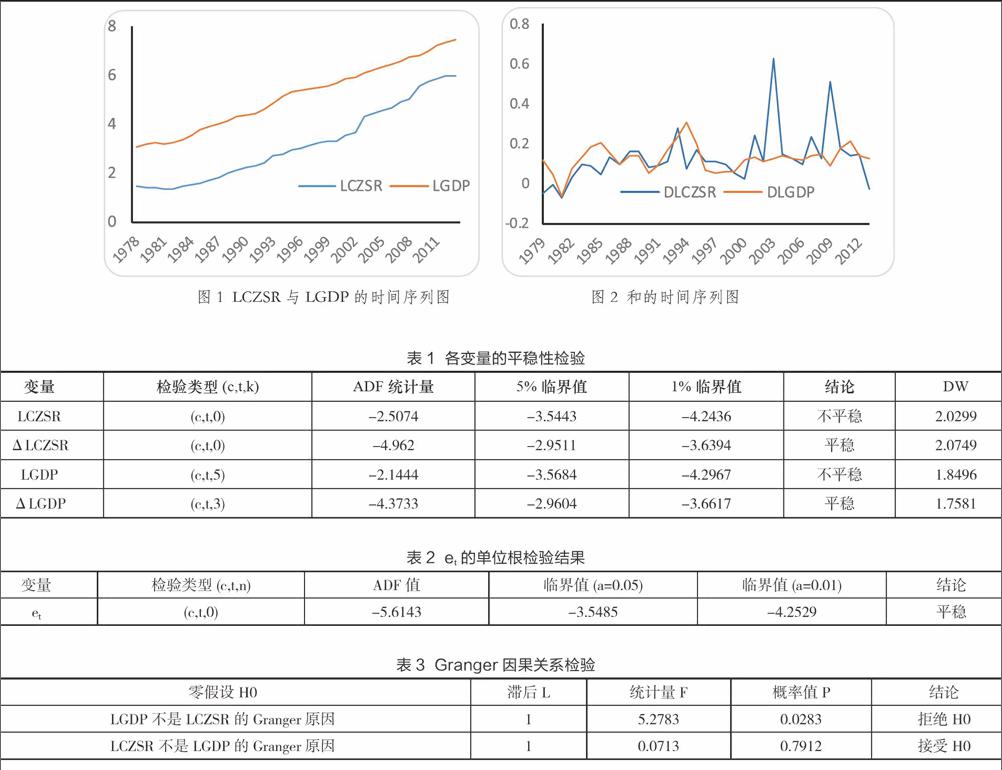
为消除数据中存在的异方差和趋势线性化现象,在不改变变量间协整关系的前提下,首先对CZSR和GDP进行自然对数变换。变换后的财政收入和GDP分别用LCZSR和LGDP表示,其时间序列图如图1。从图1可看出,LCZSR和LGDP都呈递增趋势,具有显著的不平稳性。故对LCZSR和LGDP进行一阶差分,差分后分别用和表示,其时间序列图如图2。从图2可看出,一阶差分后的两列时间序列均较平稳,可用单位根检验来证实其平稳性。
(二)财政收入与GDP的单位根检验
进行ADF检验时,根据AIC准则自动确定滞后阶数,检验结果见表1。从表1可看出,LCZSR和LGDP在5%和1%的显著水平上都是非平稳的;而其一阶差分ΔLCZSR和ΔLGDP在5%和1%的显著水平上都是平稳的。由于LCZSR和LGDP经过一阶差分均变成平稳序列,故LCZSR和LGDP都为一阶单整序列,记为I(1)。
(三)财政收入与GDP间的协整检验和误差修正模型
由单位根检验结果可知,LCZSR和LGDP均为一阶单整序列,故二者可能存在协整关系。本文采用Engle Granger两步法检验其协整关系。首先对LCZSR和LGDP进行协整回归,其回归方程为:
LCZSRt=-2.474321+1.0979LGDPt+ut(6)
R2=0.9582 A-R2=0.9570 F=779.6285 DW= 0.1902 S.E.=0.3175
由于协整回归结果DW=0.1902较小,说明可能存在自相关。因此,需加入LCZSR和LGDP的滞后因素,并重新估计LCZSR和LGDP间的协整关系。利用AIC准则确定LCZSR和LGDP的滞后阶数,得到如下模型:
LCZSRt=-0.4003+0.3441LGDPt-0.1737LGDPt-1+0.8772LCZSRt-1 +et(7)
R2=0.9942 A-R2=0.9937 F=1778.34 DW= 2.0175 S.E.=0.1213
现对et的平稳性进行检验,结果如表2。由表2可知,ADF=-5.6143,5%的临界值为-3.5485,1%的临界值为-4.2529,因为ADF小于5%和1%的临界值,所以在5%和1%的显著水平上,et都是平稳的,即et~I(0),因此,兰州市财政收入与GDP间存在协整关系。其误差修正项为:
ecmt-1=et=(LCZSRt+0.4003-0.3441LGDPt+0.1737LGDPt-1-0.8772LCZSRt-1)(8)
现将LCZSR与LGDP间的协整方程写成如下形式:
LCZSR=α+βLGDP(9)
α=-0.4003/(1-0.8772)=-3.2598
β=(0.3441-0.1737)/(1-0.8772)=1.3876
故LCZSR与LGDP间的长期协整关系方程为:
LCZSR=-3.2598+1.3876LGDP(10)
根据协整关系方程,长期内,兰州市(对数)的生产总值每变动1%,同期(对数)的财政收入将同方向变动1.3876%.
(四)财政收入与GDP的Granger因果关系检验
由于兰州市对数的财政收入和对数的GDP均为一阶单整且具有协整关系,故可检验二者的Granger因果关系,检验结果如表3:
根据格兰杰因果关系分析可知,在滞后阶数为1阶显著性水平为5%时,兰州市GDP是兰州市财政收入的Granger原因,而兰州市财政收入不是兰州市GDP的Granger原因,即兰州市GDP是兰州市财政收入的决定因素,而兰州市财政收入不是兰州市GDP的决定因素。因此,可用兰州市GDP的变化来解释兰州市财政收入的变化,且兰州市GDP的增加可以拉动兰州市财政收入的增加。
四、结论
由协整检验可知,虽然兰州市财政收入和兰州市GDP均具有非平稳性,但二者相关度较高,整体上存在长期稳定的协整关系;由误差修正模型可知,短期内兰州市财政收入和兰州市GDP间的动态调整机制可使二者自动实现内在的长期均衡。
由Granger因果检验可知,在滞后阶数为1阶时,兰州市财政收入和兰州市GDP间存在单向因果关系,即兰州市GDP是兰州市财政收入的Granger原因,而兰州市财政收入不是兰州市GDP的Granger原因。故兰州市GDP的增长是兰州市财政收入增长的决定因素,提高市内经济发展水平能够增加财政收入。
参考文献:
[1]胡秀英.抚宁县财政收入与GDP的相关分析[J].统计与管理,2015,(7):73-74.
[2]何凌云,胡振虎.我国财政收入超GDP增长的比较研究[J].财政研究,2013,(6):64-68.
[3]林国立,尚菲,张涛.蚌埠市GDP与财政收入增长关联性分析[J].蚌埠学院学报,2015,4(3):179-183.
[4]王玉华,刘贝贝.山东省GDP与财政收入的实证分析[J].东岳论丛,2009,30(7):53-58.
[5]文秀琴.河南省财政收入与GDP相关性分析[J].河南财政税务高等专科学校学报,2013,27(3):53-58.

