基于ZigBee技术的隧道人员定位精度研究

王海英+阮祺+常肖+梁鹏

摘 要：针对隧道无线传感网络技术定位人员不精确，以及定位精度容易受到网络参数设定影响的问题，通过研究ZigBee定位精度的影响因素，提出一种利用BP神经网络改进算法改善ZigBee监测网络参数设置方法。该方法可以有效快捷地架构ZigBee传感网络系统，且利用BP神经网络的改进算法预测不同参数的设置对应的定位影响精度，可以将误差稳定区域的定位误差控制在1 m以内。

关键词：ZigBee技术；RSSI定位算法；BP神经网络；定位精度

中图分类号：U458.1 文献标志码：B

文章编号：1000-033X（2016）05-0111-04

Abstract： Aiming at the problem of inaccurate positioning of the tunnel wireless sensor network， the influential factors of ZigBee positioning accuracy were studied based on RSSI algorithm and weighted centroid algorithm， and a new method of improving ZigBee monitoring network parameters was proposed by using BP neural network. The proposed method can effectively and efficiently build the ZigBee sensor network system， and the improved algorithm of BP neural network is used to predict the corresponding positioning accuracy of different parameters. Experimental results show that the error stability region can be controlled within 1 meter according to the method of parameter setting.

Key words： ZigBee technology； RSSI positioning algorithm； BP neural network； positioning accuracy

0 引 言

公路、铁路隧道的建筑施工环境艰苦恶劣，工种危险系数高，工作人员人数多，使隧道建筑施工企业面临巨大的管理困难，迫切需要一种能够高效、准确的人员定位系统。鉴于ZigBee能耗小、短距离传输稳定的优势，很多学者将该技术应用到隧道等工程定位中[1]。

但目前的研究主要是针对定位的传输方法与传输途径，并没有研究表明参数设置对定位精度的影响。由于参数设定的不同，使得定位精度存在差异，而对特殊环境中定位系统的参数设置肯定不相同。本文介绍一种利用BP神经网络算法高效优化ZigBee监测参数设置的方法，可以快捷有效地架构ZigBee传感网络系统，且利用改进算法预测不同ZigBee网络参数设置对应的定位精度，从而提高ZigBee在定位方面的应用价值。

1 基于RSSI的加权质心定位算法

传统采用RSSI定位技术的定位算法为

本文采用RSSI测量方法与质心算法相结合的定位算法，如图1所示。该定位方式首先计算出参考节点O1到被测节点的距离为d1，参考节点O2到被测节点的距离为d2，参考节点O3到被测节点的距离为d3。分别以O1、O2、O3为圆心，d1、d2、d3为半径画圆，可得交叠区域；然后，计算三圆交叠区域的3个特征点（A、B、C）的坐标，以A、B、C为顶点作三角形，定位节点D就是其质心。这种定位算法的不足是认为参与定位的参考节点对定位的影响程度一致，与现实情况不符。因此，根据RSSI测距原理分析影响定位精度的参数，并通过试验和BP神经网络模型预测定位精度，最终根据预测结果高效快捷地计算出系统最优参数配置[2-4]。

2 定位精度影响因素研究

由RSSI测距模型知，在理想条件下，影响定位精度的因素有RSSI值、A值、n值。根据CC2431数据手册，A值在30～50 dBm之间，其典型值为40 dBm；n值范围为1～8，典型值为3.375。CC2431的定位引擎并不直接使用n值，而是使用索引值n_index来替代，每一个n_index对应一个n值，n_index取0～31之间。相邻参考节点横向间距为X、纵向间距为Y、无线网络定位区域总长为L，试验参数设置如表1所示。

2.1 试验器材

试验器材主要包括11个CC2430模块，其中参考节点和协调器分别是10个和1个，CC2431模块1个以及计算机1台。

2.2 试验步骤

（1）试验参数设置。

（2）搭建试验模型。网络稳定性测试试验如图2所示，并按照图2布置参考节点（等距分布），确定定位节点的摆放位置。

（3）数据采集和统计。因隧道环境细长的结构特征，重点监测目标定位是沿隧道纵深度方向的位置进行。为了简化试验过程和分析模型，主要测量、分析目标点单方向的定位误差绝对值。

（4）数据处理和结果分析。

2.3 试验数据分析

（1）相邻2个节点间的距离X为5 m、Y为2 m时，取不同A、n_index值定位平均误差分布在0.25～49.98 m。定位误差较大的点集中在n_index等于0和30；当n_index取5～25时，定位精度都较为理想，大多数定位误差小于3 m。由图3（a）可知，当A取40 dBm、n_index取25时误差最小。

（2）相邻2个节点间的距离X为10 m、Y为3 m时，取不同A、n_index值，定位平均误差分布在0.27～45.82 m。定位平均误差小于3 m的点集中在n_index等于15～30时。由图3（b）可知，当A取45 dBm、n_index取15时误差最小。

（3）相邻2个节点间的距离X为15 m、Y为4 m时，取不同A、n_index值，定位平均误差分布在0.11～47.94 m。定位平均误差小于3 m的点集中在n_index等于15～25时。由图3（c）可知，当A取35 dBm、n_index取20时，定位误差最小。

（4）相邻4个节点间的距离X为20 m、Y为5 m时，取不同A、n_index值，定位平均误差分布在0.95～41.75 m。定位平均误差小于3 m的点集中在n_index等于15～30时。由图3（d）可知，当A取35 dBm、n_index取20时，定位误差最小。

由图3分析可得，定位精度受A、n值的影响很大。A参数的取值对定位规律准确性影响不明显，但n值对定位规律准确性影响较为明显。通常n值取3.25～4.50时，即n_index取15～25时，定位精度较高；n取1或8时，即n_index取0或30时，定位误差较大。通过对各种数值分析方法的研究和对比，发现BP神经网络具有较强的非线性映射特性，而且结构简单、可塑性强。因此，本文使用BP神经网络对定位精度进行预测，从而为ZigBee传感网络提供可靠的A、n值。

3 BP神经网络的改进算法

BP神经网络模型具有结构严谨、思路清晰、可操作性强的优点，但是BP神经网络标准算法从数学上看是一个非线性梯度优化问题，因此将出现局部最小、训练次数多而学习效率降低、收敛速度慢的问题。针对以上问题，通过引入陡度因子方法解决。

确定了试验的网络拓扑结构和训练数据后，传递函数f（x）成为影响总误差函数E的惟一特征。通过改变传递函数，调整神经元的净输入，从而改变误差函数的结构，避免陷入局部极小。BP神经网络大多采用Sigmoid型函数作为传递函数，即

理论上讲，任何一个连续的非多项式、常数函数都可以作为BP的传递函数，但是，Sigmoid函数有自身的优点，比如说鲁棒性和光滑性，以及求导时可用自身的某种形式表示，这对数值试验非常重要。权值反向传播需要得到激活函数的导数，如果有多层就有多个导数，若采用一般的连续函数，对计算机的运算和存储都是一个难题。除此之外，Sigmoid型函数的收敛速度比较快，因此选择Sigmoid函数作为传递函数，其连接权值的校正函数[4]为

陡度因子决定Sigmoid型函数的压缩程度，使其变的平坦，避免在yj（1-yj）≈0时陷入局部极小。

3.1 定位精度预测设计

定位精度预测包含训练阶段和测试阶段，方案流程如图4所示。

图4 定位精度预测系统方案流程

3.2 训练阶段

（1）样本的选择。BP神经网络建模首要前提是具有足够多且精度高的样本。考虑到预测精度和收敛速度，样本数据的数量不宜过多，因此分别选100、200、500、800组数据作为训练样本，最后通过预测结果与收敛速度的分析，确定200组为宜。

（2）网络层数的选择。选择最常用的3层神经网络结构，即输入层、输出层、隐含层。输入层包括4个神经元，即4个影响定位精度的主要因素：X、Y、A、n_index。输出层包含1个神经元即定位精度。

（3）隐含层中的神经元个数。当输入层有4个神经元时，隐含层神经元个数可以取9、10、11、12、13、14、15、16，将训练模型得到的不同预测结果进行对比与分析。

（4）传递函数。在这里选择S型正切函数tansig或S型对数函数logsig。

3.3 测试阶段

通过训练阶段对提取出来的样本进行训练之后，再对上述试验数据中的35组数据进行测试。算法流程如图5所示。

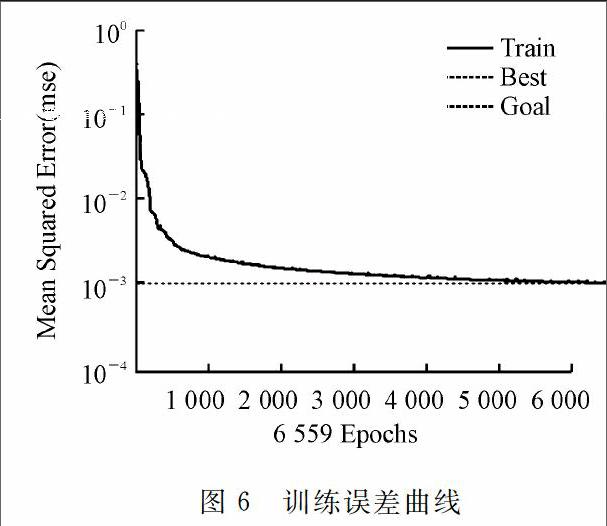
利用Matlab建立预测模型，当隐含层神经元个数为15时，平均相对预测误差最小，收敛成功率和预测准确率都比较理想，而且训练次数也不高，耗时较短。BP神经网络训练次数和预测误差成反比，训练次数越多，预测误差就会越小。想要缩短时间，就要减少运行次数，降低了预测的准确率。如果实际应用中，需要不计代价，只考虑预测准确率，则选τ=0.1为宜。如果需要运行时间短，可以考虑适量增大误差，这时选τ=0.5为宜。训练误差曲线，如图6所示。

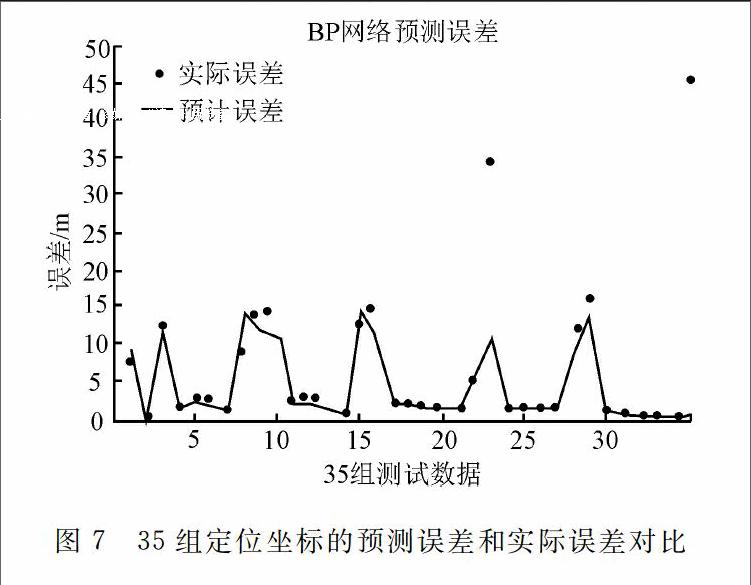
图7是35组定位坐标的预测误差和实际误差的对比图，由图可知，当定位点的实际定位坐标自身误差值小于15 m时，预测结果均比较理想。

4 结 语

本文基于ZigBee技术上研究了定位精度的影响因素，在隧道人员定位参数设置不同的情况下定位结果有差别。以上试验数据证明了井下定位误差分布的规律，运用改进的BP神经网络模型预测任意参考节点间距和A、n值对应的定位误差，通过预测值反馈得到最优参数。在井下定位中，根据最优参数设置，可以将误差稳定区域的定位误差基本控制在1 m以内，但是对于误差单向偏差区域的定位精度还有待研究。

参考文献：

[1] 马 钢.基于ZigBee的井下人员跟踪定位系统设计与实现[D].大连：大连理工大学，2008.

[2] 郭宏福，白丽娜，郭志华.2.4GHz ZigBee数传模块传输距离的估算方法[J].西安电子科技大学学报，2009，36（4）：691-695，745.

[3] 李翱翔，陈 健.BP神经网络参数改进方法综述[J].电子科技，2007，20（2）：79-82.

[4] 王美玲，王念平，李 晓.BP神经网络算法的改进及应用[J].计算机工程与应用，2009，45（35）：47-48.

[责任编辑：杜敏浩]