基于概率理论的连续管钻井调整工具面扭矩预测方法研究

李猛

(中国石油勘探开发研究院,北京 100083；中国石油钻井工程技术研究院,北京 102206)

贺会群,辛永安,熊革,张士彬,蒲晓莉

(中国石油钻井工程技术研究院,北京 102206)



基于概率理论的连续管钻井调整工具面扭矩预测方法研究

李猛

(中国石油勘探开发研究院,北京 100083；中国石油钻井工程技术研究院,北京 102206)

贺会群,辛永安,熊革,张士彬,蒲晓莉

(中国石油钻井工程技术研究院,北京 102206)

[摘要]为研究不确定性因素对连续管钻井(CTD)过程中调整工具面扭矩的影响，构建了基于概率理论的分析方法预测调整工具面扭矩的基本思想。在建立调整工具面扭矩模型的基础上，采用Monte-Carlo法对钻压、地层摩擦因数、井眼曲率等参数的随机性进行了模拟统计试验，得到了各参数及等效接触力的分布形式，并推导出调整工具面扭矩的概率分布函数。通过现场实例分析了参数的随机性对CTD调整工具面扭矩不确定性的影响，并与实测扭矩进行了对比分析。结果表明，不确定性分析方法预测的调整工具面的扭矩不是单一曲线，而是与累积概率有关的区间，区间窗口的大小与参数信息的精确程度有关，置信水平越高，扭矩预测区间的窗口越大，反之，置信水平越低，扭矩预测区间的窗口越小。预测结果与实测扭矩具有较好的一致性，说明采用概率理论预测扭矩更加科学合理。该方法对CTD定向过程中的扭矩预测以及CTD定向工具的设计及应用具有一定的指导意义。

[关键词]连续管钻井；不确定性；工具面；扭矩；接触力；概率分布

连续管钻井(CTD)是一项安全高效的钻井新技术，已经广泛应用于国外常规油气资源及煤层气、页岩气等非常规油气资源的开发，并取得了明显的经济效益[1]。由于连续管不能旋转，因此连续管只能依靠井下定向工具克服井下扭矩旋转工具面从而达到定向的目的。传统的井下扭矩预测方法一般不考虑随机性因素的影响，将模型中的所有参数均视为确定性变量来处理。但在实际的连续管钻井过程中，影响CTD定向扭矩的因素多样[2，3]，如钻压、钻井液性能、工具参数、地层参数等，受工艺水平、井下复杂环境等的影响，某些参数在空间分布上并不一定是确定值，而参数的随机性将导致CTD定向过程中扭矩的不确定性，因此，传统的扭矩预测方法存在一定的局限性。目前，国内外专家考虑不同的影响因素、采用不同的模型对CTD调整工具面所需的扭矩进行了预测计算，如Payne等考虑井下工具(BHA)变形、BHA与井眼之间的间隙、BHA重量、井斜角等影响因素，建立了调整工具面的扭矩预测模型[4～6]；Neubert等考虑动载荷对CTD调整工具面过程中扭矩大小的影响，建立了相应的扭矩预测模型[7]。然而这些预测模型中的参数在不同程度上都具有随机性和不确定性，得出的扭矩可信度不高，与调整工具面所需克服的实际井下扭矩存在较大的差别。为此，笔者引入概率统计方法[8～10]，在建立停泵及开泵条件下CTD定向过程中调整工具面的扭矩预测模型的基础上，提出了调整工具面的扭矩预测的不确定性计算方法，并以大港油田官142井为例，将实测扭矩与预测扭矩进行了对比分析。

1扭矩预测模型的建立

1.1停泵条件下CTD调整工具面的扭矩模型

图1　连续管钻井井下工具组合示意图

连续管钻井井下工具组合如图1所示，CTD定向工具上部连接MWD，定向工具末端为输出轴，输出轴下接弯螺杆+钻头。停泵时，CTD井下工具满足纵横弯曲梁分析条件[11]，设CTD井下工具组合与井壁有n个接触点，n+1跨纵横弯曲梁。为了判断定向工具输出轴以下的井下工具与井壁接触点的个数，首先进行了上切点位置的判断，假设上切点在定向工具输出轴所在位置的上部，则定向工具输出轴以下的井下工具与井壁之间只有一个接触点(除钻头外)，即弯螺杆的肘点，则只需对肘点处相邻两跨的井下工具组合受力分析即可，如图2所示。

图2　肘点处两跨井下工具的受力分析

为了进行上切点的判断，需建立三弯矩方程，采用二分法，数值迭代结果如图3所示。通常情况下，用于小井眼尺寸的螺杆钻具长度一般小于6m[11]。因此，根据图3中的数值模拟结果可得出上切点一般在定向工具的输出轴所在位置的上部，即定向工具输出轴之下只有1个接触点(除钻头外)，即弯螺杆的肘点，因此假设成立。

根据纵横弯曲量理论[11]，得到CTD弯螺杆肘点处相邻两跨井下工具在斜平面(P平面)和方位平面(Q平面)内肘点处的接触力为：

(1)

(2)

钻头处的接触力为：

(3)

(4)

图3　上切点位置

则停泵条件下调整工具面的总扭矩计算公式为：

(5)

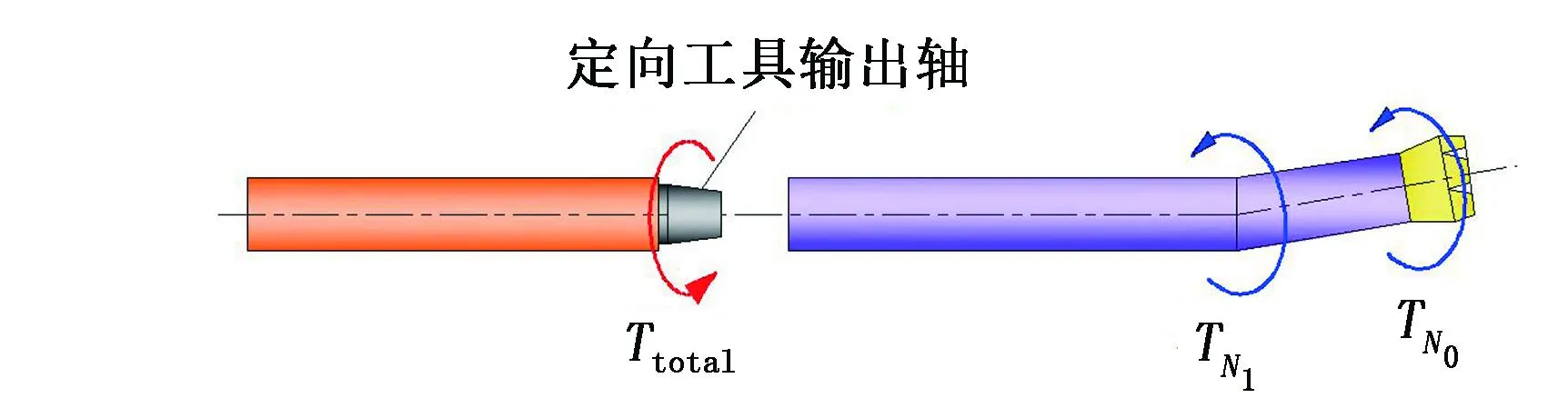
图4　扭矩示意图

总扭矩可用图4说明。

令等效接触力为：

Neq=N0+N1

(6)

则式(5)变为：

(7)

上述各式及图中参数意义如下： PB为钻压，N； N1为弯螺杆肘点处的接触力，N；N1P、N1Q分别为P、Q平面内肘点处的接触力，N；N0为钻头处的接触力，N；N0P、N0Q分别为P、Q平面内钻头处的接触力，N；Neq为等效接触力，N；Ttotal为调整工具面的总扭矩，N·m；TN0为钻头、肘点处接触力产生的扭矩，N·m； qi为第i跨的横向均布载荷，N/m；wi为第i跨钻具在钻井液中的线重，N/m；Li为第i跨钻具长度，m；Mi为第i个接触点处的弯矩，N·m； y1P、y1Q为肘点在P、Q平面内的纵坐标，m；y2P、y2Q为上切点在P、Q平面内的纵坐标，m；μr为地层摩擦因数；D0为井眼直径，mm。

1.2开泵条件下CTD调整工具面的扭矩模型

开泵钻进过程中，CTD井下工具受到钻头转动和振动等动态因素的影响，此时纵横弯曲法不再适用于CTD井下工具接触力的求取[11]。为此，Johancsik[12]提出了CTD钻进过程中受振动影响下肘点处的接触力方程。

首先，由钻压和钻具浮重引起的肘点处的接触力为：

(8)

(9)

(10)

在肘点处由钻压和浮重产生的扭矩为：

(11)

其次，根据文献[12]钻进时钻头的振动对肘点处会产生附加接触力，该附加接触力与钻头钻速有关，可表示为：

(12)

其中：

(13)

相应地，在肘点处由振动引起的附加扭矩为：

(14)

式中，α0为钻头处井斜角，(°)；KP、KQ分别为P、Q平面内的井身曲率,(°)/30m，与井斜角及方位角有关，计算方法见文献[11]； Tvb为钻头振动和转动引起的附加扭矩，N·m；Nvb为钻头振动产生的附加接触力，N；Δω为工具面角度变化量，(°)； ωb为钻头转速，rad/s；K为横向振动发生的相关系数；e1为井壁与第一跨井下工具之间的间隙，m。

另外，在钻进过程中CTD井下工具会发生轻微变形，工具变形引起的肘点处的附加接触力[13]为：

(15)

式中，s为与钻压PB有关的变形系数，CTD钻井中取0.03～0.06。

工具变形在肘点处产生的附加扭矩为：

(16)

CTD定向钻进过程中，钻头转动产生的反扭矩[14]为：

(17)

式中，Tbit为钻头扭矩，N·m。

如图5所示，开泵条件下CTD定向时调整工具面所需总扭矩为：

(18)

图5　调整工具面总扭矩

令等效接触力为：

(19)

则式(18)变为：

(20)

其中，“+”表示工具面调整方向与钻头旋向相同(开泵同向)；“-”表示两者旋向相反(开泵反向)。

2扭矩预测的随机性描述

2.1等效接触力分布形式的确定

CTD工具面调整过程中井下工具与井壁之间的等效接触力是多个参数的函数，参数具有一定的随机性，每个参数都服从一定的分布，经过大量的统计试验表明[15，16]，等效接触力的影响参数(如钻井液密度、钻压等参数)多数服从正态分布：

(21)

式中，μ为均值；σ为标准差。

部分参数(如井眼曲率、地层摩擦因数等参数)服从对数正态分布：

(22)

少数(如弹性模量、单跨长度等参数)服从均匀分布：

(23)

参数的随机性决定了等效接触力的不确定性，在分析计算的基础上，选定某些参数为变量，根据等效接触力模型建立状态函数：

Ni=gi(μ,ρm,K,E,PB,Do,…)

(24)

等效接触力的不确定性与式(24)中的各参数等随机变量事件是相关联的。

设每个参数的概率密度函数为fi(xi)，其参量为uij，如正态分布中有2个参量ui1、ui2分别表示均值μ和标准差σ，对应的累积概率函数为Fi(xi)。运用Monte-Carlo法[17]将各参数对应于各自的概率密度函数进行随机抽样，经过n=10000次模拟[18]，得到各参数的统计分布形式如图6(a)～(f)及表1所示，经过数值拟合求出停泵及开泵条件下等效接触力的拟合分布曲线，如图7所示。

表1　参数的分布形式

拟合结果显示，正态分布曲线符合等效接触力直方图概率分布，并拟合得到相应的概率密度函数：

(28)

图6　参数的分布类型

图7　井下工具等效接触力分布形式

其系数见表2。

2.2扭矩分布形式的确定

设T=h(t1,t2,…,tn)，则其累积概率函数[19]为：

(25)

式中， h-1=h-1(T,t2,…,tn)。

表2　等效接触力的分布形式

根据概率理论：

ft1,t2,…,tn(t1,t2,…,tn)=ft1(t1)ft2(t2)…ftn(tn)

(26)

则总扭矩的累积概率函数变为：

(27)

为了求取总扭矩T的概率密度函数，变换积分变量t1为T，可得：

(28)

将式(32)对T求导，可得T的概率密度函数为：

(29)

(30)

对T求导得到扭矩的概率密度函数为：

(31)

从式(31)可以看出，扭矩T服从对数正态分布，CTD调整工具面扭矩的概率密度曲线及累积概率曲线如图8所示。

3实例分析

以大港油田官142井为例，该井在钻达至井深1714m处，利用CTD电液定向工具进行定向钻井试验。该段地层与井下工具之间的摩擦因数为0.5，试验钻压5～30kN，其中正常钻进钻压为15kN，钻井液密度1.2g/cm3，弯螺杆外径104.8mm，当量内径为88.9mm，结构弯角为1.5°，井身曲率为1.5°/30m。在建立停泵及开泵条件下CTD定向过程中调整工具面扭矩模型的基础上，根据笔者建立的不确定性计算方法，首先对参数的随机性进行了统计分析，然后根据其统计结果得出等效接触力服从正态分布，随后应用概率理论推导出扭矩的概率密度函数及累积概率函数服从对数正态分布，然后对CTD调整工具面的扭矩进行了预测，并将部分预测数据与实测扭矩进行了对比分析，如图9～12所示。

调整工具面扭矩的置信区间的表示方法为[19]：

(32)

对式(32)求导得：

(33)

图9　钻压变化条件下预测数据与实测扭矩对比

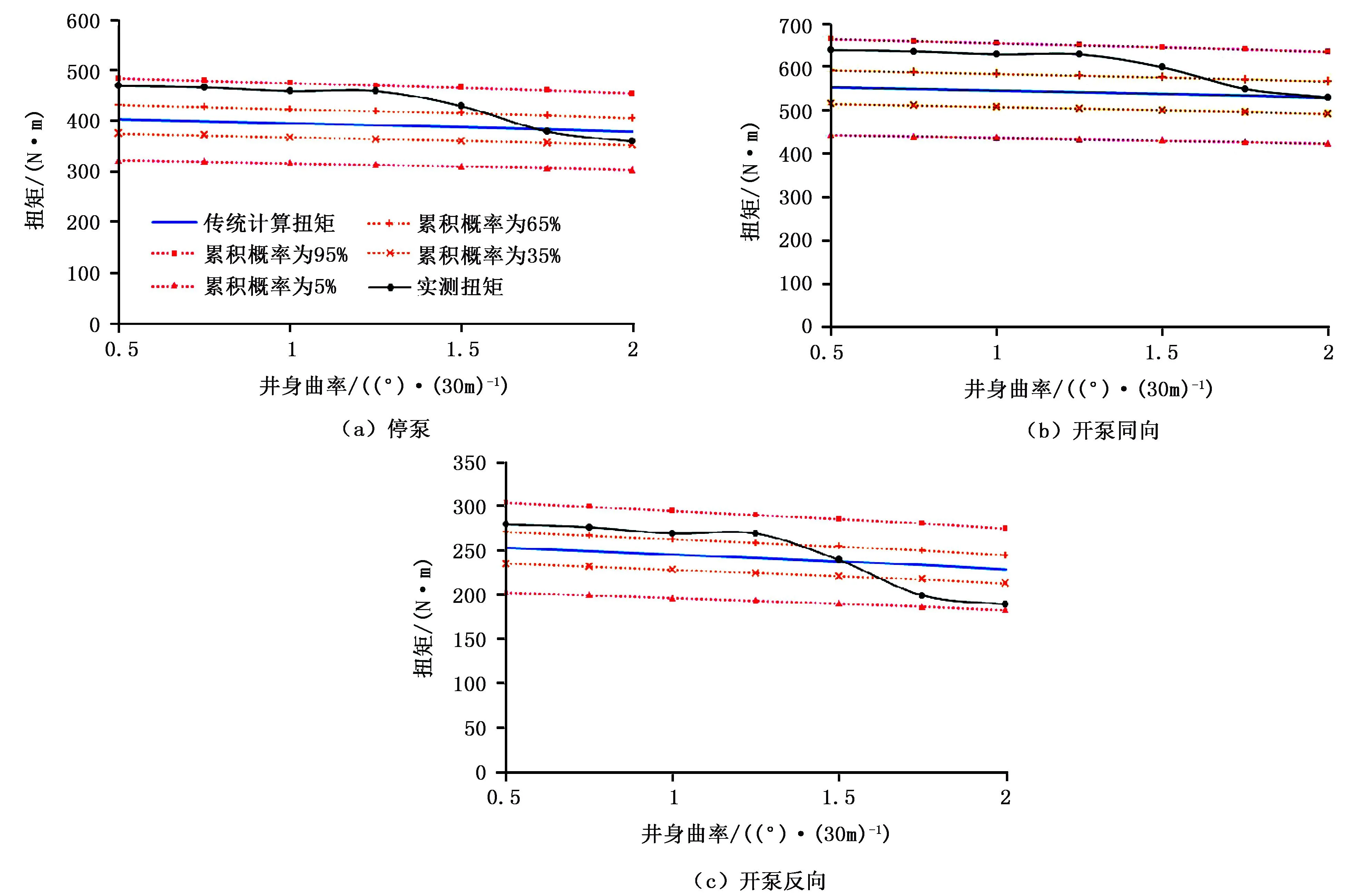
图11　井身曲率变化条件下预测数据与实测扭矩对比

图12　摩擦因数变化条件下预测数据与实测扭矩对比

累积概率为5%和95%的置信区间为90%，累积概率为35%和65%的置信区间为30%。由式(33)可以得出，置信水平越高，扭矩预测区间窗口越大，反之，置信水平越低，扭矩预测区间窗口越小；标准差越大，扭矩预测区间窗口越大，反之，标准差越小，扭矩预测区间窗口越小。因此，扭矩预测区间窗口的大小与参数资料的精确程度有关，只有获得更精确的参数资料才能减小扭矩的不确定性。由于井下条件的复杂性，往往很难获得足够精确的资料，因此，利用不确定性分析方法预测CTD调整工具面扭矩具有很强的必要性。

传统计算方法得到的工具面调整扭矩为单一曲线，而实测扭矩由于受到井下不确定性因素的影响，实测扭矩比传统单值计算方法得到的结果高或低很多；若按传统扭矩计算结果指导设计CTD定向工具，则定向工具会因输出扭矩比实际扭矩过小，而发生“转不动工具面”的情况。

不确定性方法预测得到的调整工具面所需的扭矩不是单一曲线，而是一个区间，该区间的确立更多的考虑了扭矩的各影响参数的随机性，其预测结果与实测扭矩具有较好的一致性，实测扭矩均落在预测区间之内(如图9～12所示)，若以此预测结果指导设计CTD定向工具，则定向工具的输出扭矩会完全克服实际井下扭矩，从而避免发生“转不动工具面”的情况。对于工程设计人员来说，在CTD定向过程中，对调整工具面所需扭矩可能出现的范围进行把握，比了解单一数值会更为实际和有效，调整工具面扭矩预测的不确定性方法可为CTD定向工具的设计及应用提供更加精确的指导。

4结论

1)在建立CTD停泵及开泵条件下调整工具面所需克服扭矩的模型基础上，应用Monte-Carlo法对扭矩参数进行了统计模拟试验，得出扭矩参数及等效接触力的概率分布形式。

2)基于概率理论推导出扭矩的概率密度函数及累积概率函数，得出调整工具面所需克服扭矩服从对数正态分布。

3)由于井下参数的不确定性，传统的扭矩计算方法具有一定的局限性，而由不确定性预测方法得到的扭矩不是单一曲线，而是与累积概率相关的区间，该方法的扭矩预测结果与实测扭矩具有较好的一致性，实测扭矩均落在扭矩预测该区间之内。该方法更有利于工程设计人员把握CTD调整工具面时的扭矩信息，对井下定向工具的设计及应用具有一定的指导意义。

[参考文献]

[1]李猛，贺会群，张云飞. 连续管钻井定向器技术现状与发展建议[J]. 石油机械，2015，43(1)：32～38.

[2] 秦永和，付胜利，高德利. 大位移井摩阻扭矩力学分析新模型[J]. 天然气工业, 2006, 26(11): 77～79.

[3] 郭永峰, 吴超, 廖建芳. 水平井非线性摩擦扭矩的研究[J]. 天然气工业, 1999, 19(6): 55～57.

[4] Payne M L. A study of excitation mechanisms and resonances inducing bottomhole-assembly vibrations[J]. SPE Journal,1988(3):93～101.

[5] Eric Maidla, Marc Haci. Understanding Torque: The key to Slide-Drilling Directional Wells[J]. IADC/SPE 87162, 2004.

[6] Pessier R C, Fear M J. Quantifying Common Drilling Problems With Mechanical Specific Energy and a Bit-Specific Coefficient of Sliding Friction[J]. SPE 24584, 1992.

[7] Neubert M. Lateral Vibrations in extended reach wells[J]. IADC/SPE,2000(2):23～25.

[8] 陈赓良. 对天然气分析中测量不确定度评定的认识[J]. 天然气工业，2015,32(5):70～72.

[9] Di Sciuva M, Lomario D. A comparison between Monte Carlo and FORMs in calculating the reliability of a composite structure[J]. Composite Structures, 2003, 59：155～162.

[10] 龙刚，李猛，管志川. 深井套管安全可靠性评价方法[J]. 石油钻探技术，2013,41(4)：48～53.

[11] 苏义脑，白家祉. 用纵横弯曲法对弯接头井下动力钻具组合的三维分析[J]. 石油学报，1991,12(3)：111～114.

[12] Johancsik C A. torque and drag in directional wells: prection and measurement[J]. Journal of petroleum technology, 1984(4):78～83.

[13] Omojuwa E. Integrated Dynamic Anajysis for optimal axial load and torque transfer in BHAs used for extended-reach horizontal wells[J]. SPE161064,2012.

[14] Burke J， Eller G， Venhaus D，et al. Coiled tubing drilling：Increasing horizontal reach in the Kuparuk field[J]. SPE168250，2014.

[15] O’Coonor P D T. Commentary： Reliability-past, present, and future[J]. IEEE Transactions on Reliability, 2000, 49(4)：335～341.

[16] Delgado M，Moral S. On the concept of possibility-probability consistency[J] . Fuzzy Sets and Systems, 1987, 21: 311～318.

[17] De Shun, Wen Hui, Ping Yu. New approach for reliability-based design optimization[J]. Chinese Journal of Mechanical Engineering, 2006, 19(4)：514～517.

[18] 闫相祯，高进伟，杨秀娟. 用可靠性理论解析 API 套管强度的计算公式[J].石油学报，2007，28(1)：122～126.

[19] 孙志礼，陈良玉. 实用机械可靠性设计理论与方法[M].北京：科学出版社，2003.

[编辑]张涛

[文献标志码]A

[文章编号]1673-1409(2016)10-0061-11

[中图分类号]TE973.1

[作者简介]李猛(1986-)，男，博士生，现从事连续管钻井井眼轨迹控制方面的研究工作；E-mail：limengti06@126.com。

[基金项目]国家科技重大专项(2011ZX05036-006)。

[收稿日期]2015-12-19

[引著格式]李猛，贺会群,辛永安,等.基于概率理论的连续管钻井调整工具面扭矩预测方法研究[J].长江大学学报(自科版)，2016,13(10)：61～71.