基于双向配置方向过流继电器的反时限后备保护优化整定策略
胡 傲 ,黄景光 ,翁汉琍 ,宫娅宁 ,苏 舒 ,林湘宁
(1.三峡大学 电气与新能源学院,湖北 宜昌 443002;2.华中科技大学 强电磁工程与新技术国家重点实验室,湖北 武汉 430074)
0 引言
电力系统的优化整定计算问题实质是为了电网更好地安全稳定运行,满足更高的“四性”要求[1]。整定计算是否准确决定了保护装置切除故障的能力。我国现阶段保护系统的配置仍然是以定时限保护为主,文献[2]指出它的保护范围受系统运行方式以及电网接线方式影响比较大;文献[3]指出在具有多级保护的线路中,离电源端越近,保护的速动性就越差,保护动作时间就越长;文献[4]指出在重负荷线路中,其灵敏度系数较低,发生近端故障时且主保护拒动的情况下,轻者会丢失大量负荷,并导致同断面其他线路严重过载威胁设备安全,重者则会引起系统性安全事故甚至电网解列。
定时限的诸多问题使得国内外学者纷纷寻找另一种特性的保护,即反时限保护,它反映了电流与时间之间反比的关系,它的选择特性避免了与灵敏性的冲突,且反时限保护的经济可靠[5]等优点使其在欧美电网保护中有了较好的应用,但反时限继电器在整定计算方面仍然存在一些问题。
国内外对于复杂环网的整定计算研究起步较早,早在20世纪80年代就有学者把继电器的参数整定计算抽象为利用数学算法转化为优化问题求解,文献[6]提出了优化整定的概念,即确定一个目标函数和若干个约束条件,求出反时限过流保护全局最优解。然而由于电力系统结构复杂多变,为了更准确地反映所对应的结构,在整定计算中又相应添加约束条件,这使得计算过程变得复杂。文献[7-8]提出首先对约束条件进行处理,通过分析继电器间的配合关系以及保护参数的约束关系,排除一些不必要的约束,一定程度上加速了整定流程;文献[9]将故障位置的变化可能引起保护对的变化考虑进来,从不失配的角度全面分析了所有相邻保护,做到了精确配合,无一遗漏;文献[10-15]从理论上介绍了数学规划法求解全局最优解,但对于非线性、离散变量问题容易陷入局部最优解;文献[16-18]克服了数学规划法的困境,采用更加先进的智能优化算法,操作简单,容易建模。
方向过流继电器因其经济实用的特点在传统整定计算方案中得到了广泛应用,同时,它还能定向判断故障电流避免保护误动,这在单侧电源供电的辐射形电力系统中无疑是最佳选择。但在环网系统中,由于网络结构复杂,加之故障电流为双向流动,这种只配有一套方向过流保护的继电器显然不能同时反映2个方向的故障电流。因此美国Easun Reylloe电气公司设计制造出一种新型继电器,即双向配置方向过流继电器,它弥补了单向过流继电器的缺陷,可以同时反映2个方向的故障电流,改变了传统方案中的主、后备保护对,给复杂环网整定计算带来了新思路。
本文采用改进型粒子群优化算法对双向过流继电器实现参数整定计算,针对反时限过流保护在各种故障状态下保护间的选择性问题,提出了保护间参数约束条件和保护判据,有效地保证了任意故障下保护的选择性。
1 基于反时限特性的新型过流继电器
1.1 反时限特性及标准
反时限保护在性能上优于阶梯型折线的定时限保护,在保证选择性的同时,又能克服定时限近电源端保护时间偏大的情况,目前关于反时限特性继电器的标准有IEC255-03与IEEE Std C37.112—1996 2种,本文主要采用国际电工委员会标准,通用公式如下:
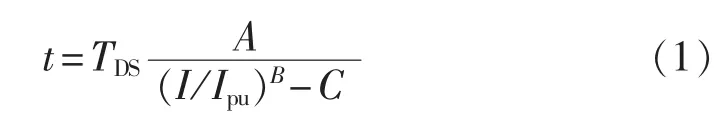
其中,t为继电器的动作时间;TDS为继电器时间整定系数;I为流过继电器的实际电流值;Ipu为继电器的启动电流;A、B为不同反时限特性方程所取常数,普通反时限特性取A=0.14、B=0.02,非常反时限特性取 A=13.5、B=1,极端反时限特性取 A=80、B=2;C 通常为1。
1.2 双向配置方向过流继电器的工作原理
双向配置方向过流继电器配备了2套反时限特性保护,为便于区分,将2个方向一个规定为正向,另一个规定为反向,且每套反时限保护的参数根据各自方向设定,通常正向保护在线路发生故障时首先动作,当其失灵时,反向保护作为备用保护切除故障。这里所说的正向和反向保护并非同一继电器内的2套保护,而是主、后备保护对的2套保护。
双向配置方向过流继电器的应用改变了以往寻求主、后备保护对的方法,它是根据一种就近后备的原则,即连接在同一条母线不同线路的所有双向配置方向过流继电器。根据这种原则得出的主、后备保护对不同于传统方案里继电器间跨越式的联系,其不仅拉近了保护对之间的距离,而且当故障发生且主继电器失灵时,备用继电器在一定程度上提升了系统速动性。
对于复杂的环网系统,由于传统的方向过流继电器只能判别来自初始设置方向的故障电流,所以其作为后备继电器并不占有优势,而双向配置方向过流继电器则弥补了传统单向继电器的不足,它可以充分发挥就近后备的优势,从而在速动性方面有了很大改善。
图1为含6个传统方向过流继电器的三母线系统实例,该方案下的保护配置方式见表1。例如,当故障发生在点A时,R1作为主继电器动作,如果R1拒动,则R5作为备用继电器动作;同样地,点A故障时,R2将作为主继电器负责隔离故障,当其拒动时,R6便作为后备保护动作。

图1 含传统方向过流继电器的三母线系统Fig.1 Three-bus system with conventional directional overcurrent relays
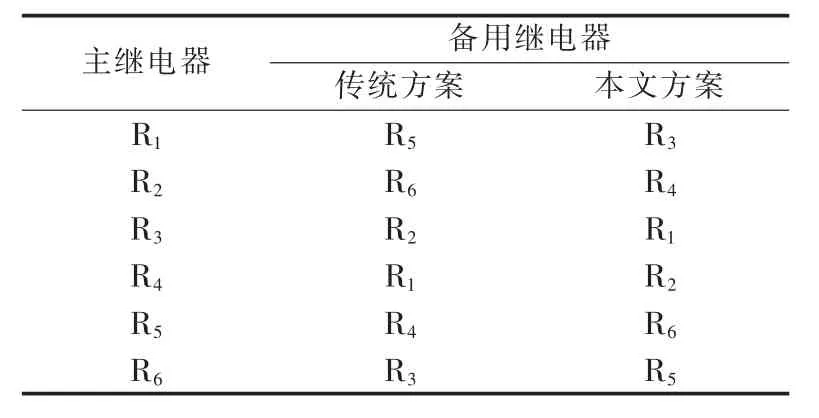
表1 传统保护方案与本文所提保护方案的主、备用继电器Table1 Primary and backup relays for conventional and proposed protection schemes
双向配置方向过流继电器具备高灵活性和协调能力的优点,当线路发生故障时,继电器会在正、反2个方向动作,其时间特性如图2所示。当故障电流按设定的正方向流动时,继电器将作为主保护,相反则作为后备保护。继电器有2对不同的参数设置:作为主保护参数作为后备保护参数。图3为含6个双向配置方向过流继电器的三母线系统实例,该方案下的保护配置方式见表1。例如,当故障出现在点A时,R3将作为R1的后备保护,R4将作为R2的后备保护。同样,对于相同的故障定位,当R1启动正向动作保护时,R3将启动反向动作保护。
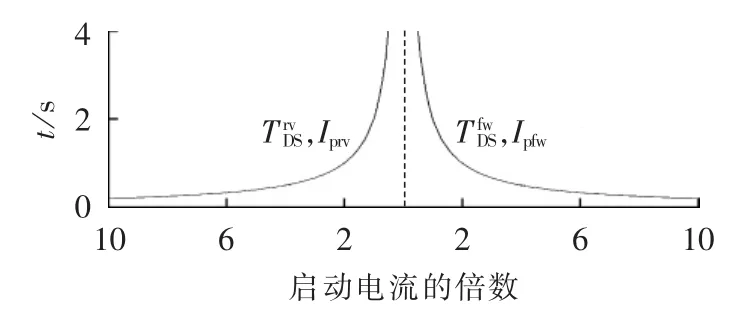
图2 双向配置方向过流继电器的时间特性Fig.2 Time characteristic of bidirectional overcurrent relay

图3 含双向配置方向过流继电器的三母线系统Fig.3 Three-bus system with bidirectional overcurrent relays
2 反时限后备保护优化整定策略
2.1 基于双向配置方向过流继电器的整定配合方案
前文已指出现阶段应用定时限保护的环网整定策略存在的一些问题,而反时限保护的应用在很大程度上解决了定时限保护的不足,加之双向配置方向过流继电器是依据反时限特性设计制造,因此在研究反时限后备保护优化整定策略时其理当为首选。
过流继电器的动作时间与其短路电流呈反比例函数关系,如式(2)所示。

其中,i表示继电器标识符;j表示故障位置标识符;常数参数A和B通常随着过流继电器类型的变化有不同取值,本文将 A设置为 0.14,B设置为0.02;Iscij为流过继电器的故障电流;Ipi为启动电流。如第1节所述,每个双向配置方向过流继电器都有一对主、后备动作装置。最优目标是在满足所有保护配置原则下最小化继电保护装置的动作时间。目标函数可描述为式(3)。

其中,Ω为主、后备继电器的集合;N为继电器总数;M为所有馈线故障点总数;tfwij和trvkj分别为对于故障点j,继电器Ri的正向动作时间与继电器Rk的反向动作时间,其线性关系可分别描述为式(4)和式(5)。
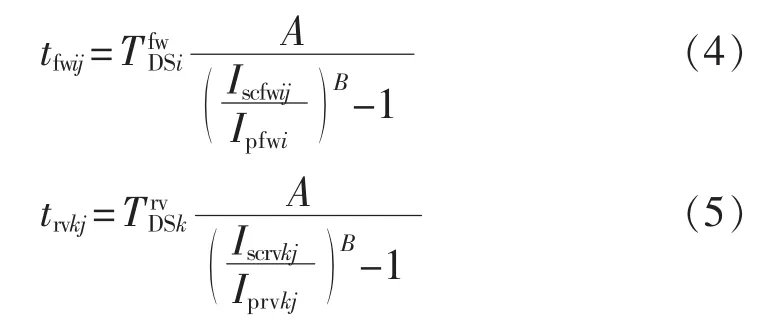
其中分别为继电器Ri和Rk的正向时限整定值和反向时限整定值;Ipfwi和Iprvk分别为继电器Ri和Rk的正、反方向启动电流;由于故障点j的故障电流通过正向继电器Ri,因此被标识为Iscfwij,同理由于故障点j的故障电流通过反向继电器Rk,因此被标识为Iscrvkj。解决保护配置问题必须满足下式:

其中,dCTI为协调时间间隔(CTI),表示主继电器动作和备用继电器动作时间差最小值,为在任意故障下满足选择性要求,将在2.2节专门讨论。此外这些定值也要满足约束条件,可描述如下:

其中,Ipi_min和Ipi_max分别为继电器Ri启动电流的最小和最大值;TDSi_min和TDSi_max分别为继电器Ri的时限整定值的最小值和最大值。
保护配置需要优化的2个主要变量为2个方向的 TDS和 Ip,从式(4)和式(5)中可以看出,继电器的动作时间和启动电流之间是非线性关系。因此,优化模型可以被描述为一个非线性规划问题。
2.2 同种类型特性曲线在任意故障情况下满足选择性的保护判据
为避免发生保护间抢动,主、后备保护之间应留有一定的时间间隔。由于反时限过流保护的动作时间与短路电流呈非线性关系,在某种故障下主、后备保护有正确的配合关系并不能保证在任意故障情况下满足选择性。如图4所示,保护R1是保护R2的后备保护,在近端故障时,短路电流较大,两保护动作关系正确;但随着故障位置逐渐远离电源点,短路电流逐渐减小,保护R1的动作时间比R2的动作时间增加得更慢,保护间失去选择性。当保护满足任意故障下的选择性时,则动作特性曲线不存在交点。

其中,Δt为主、后备保护动作时间差;t1为后备保护R1的动作时间;t2为主保护R2的动作时间。

图4 不满足选择性的动作特性Fig.4 Operative characteristic when selectivity is not satisfied

式(10)为一元一次函数,当斜率k<0时,在故障电流数值很大的情况下,y<0,不能满足选择性要求,因此必须满足k>0。
记 Ip_max=max{Ip1,Ip2},当 Ip_max可以令 y>0 时,能保证在任意故障电流下都满足式(10),将Ip_max=Ip1、Ip_max=Ip2分别代入式(10)得到在整个保护范围内都满足式(10)的参数关系为:

保护系统中,主、后备保护往往采用相同类型的反时限特性曲线,即特性曲线常数A和B取值相同。将式(1)代入式(9),则满足式(9)等价于满足:
在式(11)的约束下有<0,主、后备保护动作时间之差随故障电流的减小而单调递增。
因此,主、后备保护采用同种动作特性时,只要在最严重预想事故下满足选择性要求,式(11)就可作为保护在任意故障情况下满足选择性的参数约束条件,如图5所示。

图5 满足参数约束的动作特性Fig.5 Operative characteristic when characteristic parameter constraints are satisfied
3 算例验证
采用双向配置方向过流继电器的反时限保护方案进行IEEE 30节点部分系统仿真实验,如图6所示。
图6所示系统有3个132 kV/33 kV、总容量为50 MV·A的变电站,链接母线2、8和12。变电站33 kV侧装配了28个方向型过流继电器,每个分布式电源按额定5 MV·A工作且功率因数全部统一。分布式电源机组进线系统通过一个480 kV/33 kV的升压变压器,其暂态电抗为5%,节点设置在所有线路的中点位置(F15—F30),便于进行三相短路分析。
通过MATLAB对继电器参数实现整定计算,本文摘取部分节点的整定结果。表2、表3分别为传统和新方案下的继电器参数设置,表中电流均为标幺值。通过数据对比发现,新型继电器的参数整定发生很大变化,明显可看出摆脱了传统继电器的一套保护既充当主保护又充当备用保护的特点,且备用保护和主保护之间有一定时间间隔,避免了保护发生误动。这是因为传统方案里R1只配备了1套保护,它既要满足作为主继电器的约束条件,同时也要满足作为R14的备用继电器的约束条件,需要指出的是,同样是R1,当其配备了2套保护时,不论作为主继电器还是备用继电器,它都有其对应的保护,从而能更有效地发挥其性能。

表2 传统保护方案的TDS与Ip最优设置Table 2 Optimal settings of TDSand Ipfor conventional protection scheme

图6 IEEE 30节点系统图Fig.6 IEEE 30-bus system

表3 本文所提继电器方案的参数设置Table 3 Settings for proposed protection scheme
从图7可以很直观地看出,利用双向配置方向过流继电器保护的动作时间明显优于传统保护方案,尤其当故障发生在点F20—F24时,保护的动作时间平均缩减50%以上,这与就近选取备用保护密切相关。例如,当点F18故障时,主继电器R10和R16分别动作,如果R10拒动,则它的备用继电器R9和R11(在传统方案中R6和R22是其备用继电器)分别动作,R17作为R16的备用继电器动作(当R16拒动时)。通过图7中F18的柱状图可以看出,应用新保护方案可以更迅速地切除故障。相比传统保护配置方案,新方案中备用继电器不再跨越整条线路,这无疑缩减了故障电流的传播时间。新方案的仿真结果展示出绝对的优越性。通过计算,在F15—F25分别发生故障时,传统保护中继电器总的动作时间为46.933 6 s,而应用了双向配置方向过流继电器后,动作总时间为25.0461 s,双向配置方向过流继电器可以实现更快的故障隔离。

图7 2种保护方案的主、备用继电器最优动作时间Fig.7 Comparison of total operation time between two schemes
4 结论
本文运用双向配置方向过流继电器,建立了反时限保护整定计算模型。PSCAD仿真验证表明,本文方案提高了保护的速动性。此外,本文还提出了同种类型特性曲线在任意故障下满足选择性的保护判据,从而避免了保护误动、抢动;同时还基于双向配置方向过流继电器提出了就近后备的概念,使复杂环网在寻求主、后备保护对时更加简单、准确,从一定程度上提高了环网整定计算的效率,不受网络结构的限制,改进了优化整定的方法。
参考文献:
[1]国家电力调度通信中心.电力系统继电保护规定汇编[M].北京:中国电力出版社,1997:47-48.
[2]郭煜华,姜军,范春菊,等.改进的配电网反时限过电流保护[J].电力自动化设备,2015,35(10):45-50.GUO Yuhua,JIANG Jun,FAN Chunju,et al.Improved inversetime over-current protection for distribution network[J].Electric Power Automation Equipment,2015,35(10):45-50.
[3]张保会,尹项根.电力系统继电保护[M].2版.北京:中国电力出版社,2009:18-30.
[4]汤涌,卜广全,易俊. 印度“7.30”、“7.31”大停电事故分析及启示[J]. 中国电机工程学报,2012,32(25):167-174.TANG Yong,BU Guangquan,YI Jun.Analysis and lessons of the blackout in Indian Power Grid on July 30 and 31,2012[J].Proceedings of the CSEE,2012,32(25):167-174.
[5]CHUNG J L,LU Y,KAO W S,et al.Study of solving the coordination curve intersection of inverse-time overcurrent relays in subtransmission systems[J].IEEE Transactions on Power Delivery,2008,23(4):1780-1788.
[6]URDANETA A J,NADIRA R,PEREZ JIMENEZ L G.Optimal coordination of directional overcurrent relays in interconnected power systems[J].IEEE Transactions on Power Delivery,1988,3(3):903-911.
[7]KAREGAR H K,ABYANEH H A,OHIS V,et al.Pre-processing of the optimal coordination of overcurrent relays[J].Electric Power Systems Research,2005,75(2):134-141.
[8]EZZEDDINE M,KACZMAREK R.Reduction of effect of coordination constraints in the linear optimization of operating times of overcurrent relays[C]∥MELECON 2008-The 14th IEEE Mediterranean Electrotechnical Conference,2008.Ajaccio,France:IEEE,2008:707-712.
[9]AGGARWAL C,MANGALVEDEKAR H A,CHAUDHARI H B.Effect of fault location on optimal coordination of directional over current relay[J].TENCON 2008-2008 IEEE Region 10 Conference,2008.Hyderabad,India:IEEE,2008:1-5.
[10]ELREFAIE H B.A parallel processing algorithm for coordination of directional overcurrent relays in interconnected power systems[J].IEE Proceedings-Generation,Transmission and Distribution,1994,141(5):514.
[11]CHATTOPADHYAY B,SACHDEV M S,SIDHU T S.An on-line relay coordination algorithm for adaptive protection using linear programming technique[J].IEEE Transactions on Power Delivery,1996,11(1):165-173.
[12]URDANETA A J,RESTREPO H,MARQUEZ S,et al.Coordination ofdirectionalovercurrentrelay timing using linear programming[J].IEEE Transactions on Power Delivery,1996,11(1):122-129.
[13]BIRLA D,MAHESHWARI R P,GUPTA H O.A new nonlinear directional overcurrent relay coordination technique,and banes and boons of near-end faults based approach[J].IEEE Transactions on Power Delivery,2006,21(3):1176-1182.
[14]李滨,韦化,李佩杰.电力系统无功优化的内点非线性互补约束算法[J]. 电力自动化设备,2010,30(2):53-58.LI Bin,WEI Hua,LI Peijie.Interior-point nonlinear algorithm with complementarity constraints for reactive-power optimization[J].Electric Power Automation Equipment,2010,30(2):53-58.
[15]ZEINELDIN H,EL-SAADANY E F,SALAMA M A.Optimal coordination of directional overcurrent relay coordination[C]∥IEEE Power Engineering Society General Meeting,2005. [S.l.]:IEEE,2005:1101-1106.
[16]刘述奎,李奇,陈维荣,等.改进粒子群优化算法在电力系统多目标无功优化中应用[J]. 电力自动化设备,2009,29(11):31-36.LIU Shukui,LI Qi,CHEN Weirong,et al.Multiobjective reactive power optimization based on modified particle swarm optimization algorithm[J].Electric Power Automation Equipment,2009,29(11):31-36.
[17]MANSO UR M M,MEKHAMER S F,EL-KHARBAWE N.A modified particle swarm optimizerfor the coordination of directional overcurrent relays[J].IEEE Transactions on Power Delivery,2007,22(3):1400-1410.
[18]周任军,李绍金,李红英,等.空间粒子群优化算法及其在电力系统环保经济负荷分配中的应用[J].电力自动化设备,2014,34(9):7-12.ZHOU Renjun,LI Shaojin,LI Hongying,et al.Space particle swarm optimization algorithm and its application in environmental&economic load distribution of power system[J].Electric Power Automation Equipment,2014,34(9):7-12.

