三维覆冰斜拉索风致振动驰振分析

谭冬梅， 王凯丽， 瞿伟廉， 韩　玲， 高远志

(1.武汉理工大学 土木工程与建筑学院，武汉　430072； 2.湖北省建筑科学研究设计院，武汉　430071)



三维覆冰斜拉索风致振动驰振分析

谭冬梅1， 王凯丽1， 瞿伟廉1， 韩玲2， 高远志1

(1.武汉理工大学 土木工程与建筑学院，武汉430072； 2.湖北省建筑科学研究设计院，武汉430071)

摘要：斜拉索偏心覆冰后，气动外形不再稳定，在风的作用下，可能诱发驰振;大幅的驰振将威胁到拉索的结构安全，因此，有必要对覆冰斜拉索的驰振稳定性进行深入的研究。应用FLUENT中的SST k-ω模型对三维覆冰斜拉索的绕流场进行数值模拟，得到全攻角下的阻力系数、升力系数及驰振力系数，依此判定覆冰斜拉索是否发生驰振，并得到某大跨斜拉桥部分斜拉索的驰振临界风速。结果表明：经过三维模拟计算的覆冰斜拉索的部分驰振力系数小于零，并且驰振临界风速较小，斜拉索易发生覆冰驰振；与风洞试验和二维模拟数据比较，三维覆冰斜拉索模拟获得的气动力系数比二维更接近试验值。

关键词：覆冰；斜拉索；气动力参数；驰振；临界风速

大跨斜拉桥由于过冷却水附着在拉索表面，致使拉索表面被包裹上冰层。拉索偏心覆冰后，气动外形不再稳定，在风的作用下，可能诱发驰振。驰振是由于平均升力系数突降产生的气动负阻尼引起的一种横风向风致振动，属发散性振动，对结构破坏很大。近年来，很多专家对覆冰导线的驰振进行了大量的研究，主要有Den Hartog[1]机制和Nigol[2]机制，前者认为气动负阻尼是驰振的关键原因，后者认为是冰翼气动力产生的扭转自激失稳。李万平等[3-4]曾对覆冰导线空气动力特性进行了测试；严波等[5-6]对四分裂导线的舞动特性和尾流驰振进行了数值模拟研究；Braun等[7]利用数值模拟分析了双分裂、三分裂和六分裂导线的绕流场。

覆冰斜拉索由于其动力特性与覆冰导线有差异，并且斜拉索与水平方向成较大的夹角(一般>30°)，其风攻角可为0°～360°，较易满足驰振的起振条件[8]，因此，覆冰导线驰振不同于覆冰斜拉索驰振。Demartino等[9-10]利用风洞试验研究了桥梁拉索覆冰的不同类型，分析了覆冰对拉索气动参数的影响和覆冰拉索的驰振稳定性；李寿英[11]对覆冰拉索进行了风洞试验和二维模拟研究。但是，当ReD>250时，二维模拟计算的气动参数会出现错误值，三维模拟计算对正确预测流动特性是有必要的[12]，为验证三维覆冰拉索模拟的精确性，本文运用FLUENT软件，对三维新月形覆冰斜拉索的绕流场进行数值模拟，获得Den Hartog系数和斜拉索驰振临界风速，并与二维和风洞试验数据进行比较，证明计算流体力学(Computational Fluid Dynamics,CFD)可以成为替代风洞试验研究驰振的一种高效手段，也为进一步的覆冰拉索风致振动研究提供数据。

1横向驰振原理及临界风速计算

1.1气动力参数

气动力参数采用如下定义：

CL=2FL/(ρU2LB)

(1)

CD=2FD/(ρU2LB)

(2)

式中：FL为斜拉索模型的升力，来流速度方向逆时针转动90°为升力的正方向；FD为斜拉索模型的阻力，沿来流方向为正；ρ为空气密度，取为1.225 kg/m3；U为前方均匀来流风速；B为斜拉索模型截面特征长度；L为斜拉索模型长度；CL、CD分别为升力系数和阻力系数。

1.2风致斜拉索横向驰振原理

偏心覆冰拉索在风的激励下，在其上产生升力，诱发驰振。一个振动系统是否稳定，取决于其阻尼项的正负，当系统的阻尼项为正时，系统稳定；反之，系统失稳[13]。依据Den Hartog驰振理论，当气动力为负阻尼时结构发生失稳，即驰振发生的描述为：

(3)

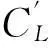
1.3临界风速计算方法

当气动阻尼与结构阻尼之和为零时为驰振发生的临界状态，则可得驰振临界风速的理论公式为[14]：

(4)

式中：m为振子质量；ω为结构振动圆频率；ξ为阻尼比。

由于拉索的一阶模态频率最小，相应驰振临界风速最小，因此，应计算拉索一阶模态相对应的驰振临界风速。则第一阶模态驰振临界风速可由下式得到：

(5)

式中：m1为单位长度斜拉索质量；ω1为斜拉索一阶模态圆频率;ω1=2πf1;f1取斜拉索一阶模态频率;ξ1为斜拉索一阶模态的阻尼比。

2模型建立与数值模拟方法

2.1模型的建立

覆冰斜拉索选取新月形典型冰型，斜拉索直径为120 mm，覆冰厚度为50 mm，拉索模型长度为900 mm，其模型外形尺寸见图1。计算流域采用矩形区域，计算区域的大小为3.4 m×5.1 m，拉索的中心放置于原点处，距离上游流体入口为1.7 m，距离下游流体出口为3.4 m，

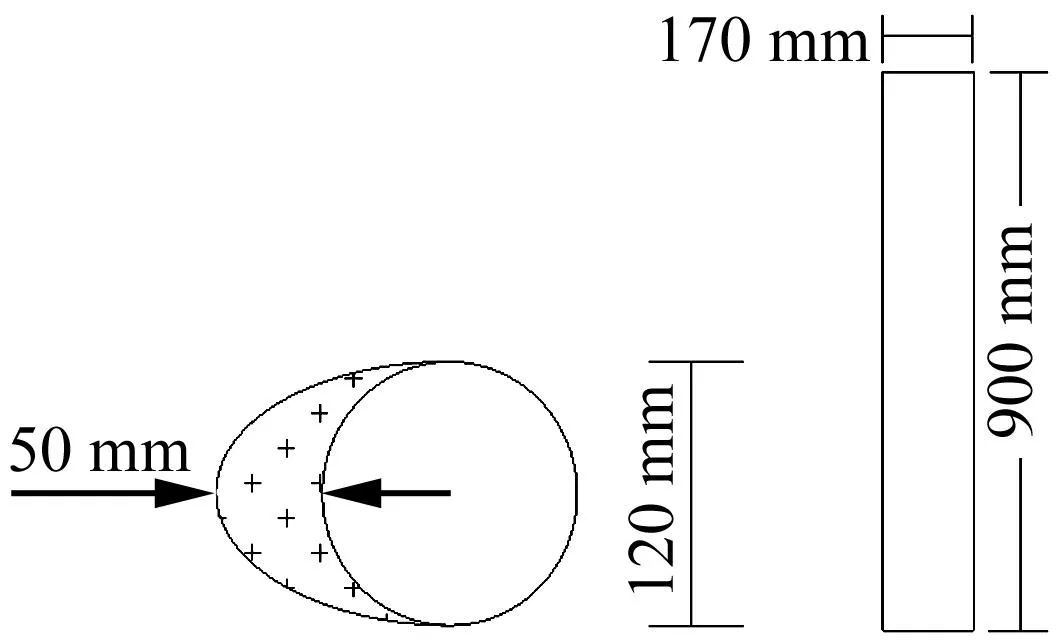
图1　三维覆冰拉索模型示意图Fig.1 Sketch of 3D stay cables with iced accretion model

距离左右流域壁面均为1.7 m，详见图2，图中X轴正方向为速度来流方向，来流方向逆时针转动90°为Y轴正方向，Z轴为拉索的长度方向。

图2　计算区域尺寸及坐标Fig.2 Computational domain size and coordinate

三维拉索绕流的网格采用结构化网格，拉索周围边界层网格采用外O形网格，对边界层网格进行加密，边界层径向网格增长系数为1.05，网格划分见图3。

图3　覆冰拉索网格划分Fig.3 Mesh of iced cable

2.2数值模拟方法

边界条件的定义：上游流体入口定义为速度入口(Velocity inlet)，下游流体出口定义为压力出口(Pressure outlet)，上下壁面定义为对称边界(Symmetry)，其他定义为固壁边界(Wall)。进口速度为12 m/s，湍流强度(Turbulent Intensity)设置为3.8%，湍流黏性率(Turbulent Viscosity Ratio)设置为10。

求解器(Solver)选用基于压力法的求解器(Pressure Based)，三维空间(3D)，采用非稳态计算方法，时间步长取0.001s。湍流模型采用SSTk-ω(Shear Stress Transportk-ω)模型，松弛因子采用默认，动量、湍动能、比耗散采用二阶迎风格式，SIMPLEC算法。

模拟计算时取5°攻角递增，经过计算后，为增加计算精确度，在升力系数曲线的明显尖峰处增加计算工况，取2°攻角递增，风攻角示意图见图4，为了使模拟更精确，针对每一工况进行建模、划分网格。

图4　风攻角示意图Fig.4 Diagram of wind attack

3三维新月形覆冰斜拉索数值模拟结果

3.1典型风攻角下流场分布

为了分析拉索展向不同位置处的表面风压，取模型展向六个监控截面，监控截面分别为Z=100 mm、Z=200 mm、Z=300 mm、Z=400 mm、Z=500 mm、Z=600 mm。

图5给出了同一时刻90°风攻角下监控截面的压力云图，从图5可知,不同截面脱落旋涡中心的颜色有深有浅，说明其压力值不一致，并且脱落散发形式也有着细微的差别，随着拉索高度变化，相应截面的压力云图是存在相位差的，说明了空间拉索绕流场的三维流动特性，这在二维模拟中是无法反应到的，因此，三维模拟比二维模拟更接近于实际流动特性。

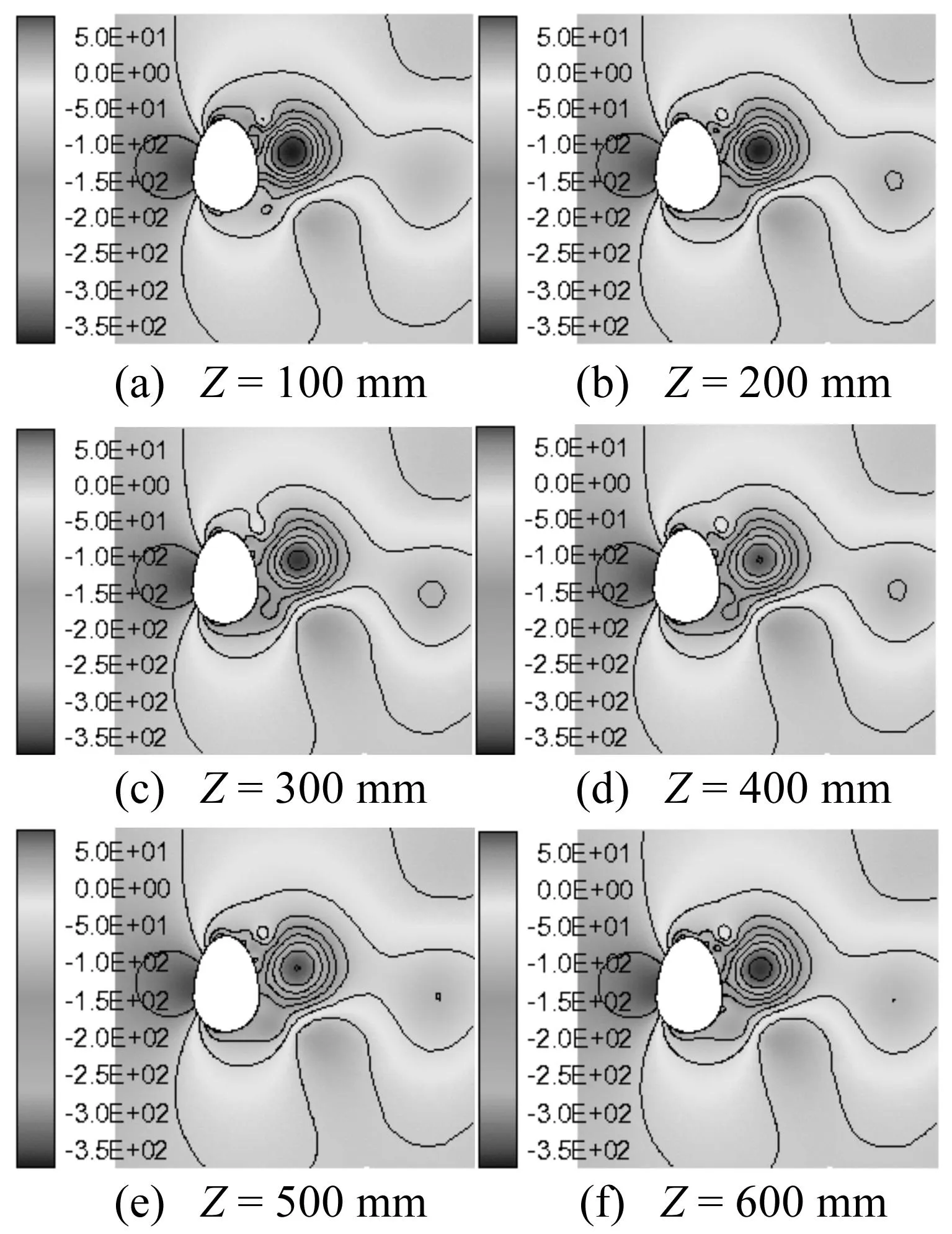
图5　90°风攻角监控截面的压力云图(单位：Pa)Fig.5 Pressure contour of monitoring section of 90°wind attack(unit: Pa)

图6所示为0°、90°风攻角时的速度分布，由图6可知，有明显的尾流涡交替现象。在拉索迎风面和背风面速度较小，迎风的两侧速度较大，而压力在迎风面出现最大值，背风面出现最小值。

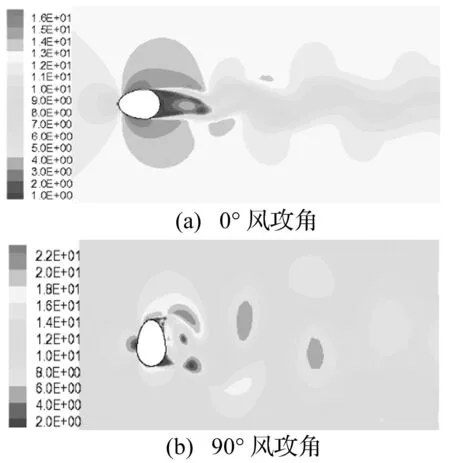
图6　典型风攻角的速度分布(单位：m/s)Fig.6 Velocity contour of typical wind attack(unit: m/s)

3.2全攻角下三维覆冰拉索的气动力系数

图7分别是三维FLUENT模拟获得的0°风攻角和90°风攻角时阻力系数和升力系数时程曲线。在0°风攻角时，随着稳定涡街和旋涡脱落的形成，阻力系数达到稳定，约为0.48，而升力系数在0附近呈稳定的周期变化；在90°风攻角时，随着周期性的旋涡脱落，阻力系数在1.6附近呈周期变化，升力系数在-0.1附近呈周期性变化。由升力系数时程曲线进行傅里叶变换，即可得到旋涡脱落频率和Strouhal数，为涡激共振研究提供参考。

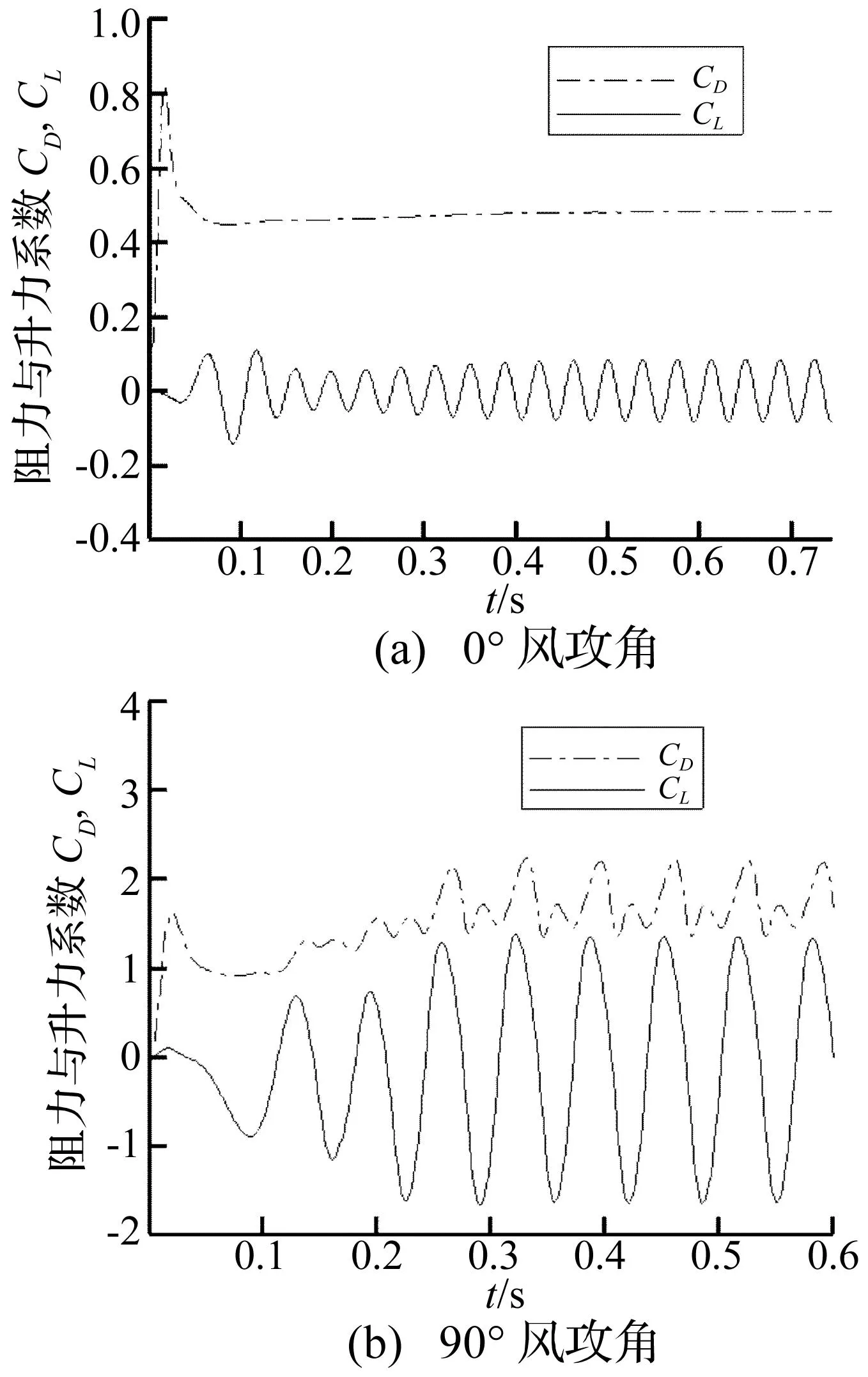
图7　典型风攻角的阻力系数和升力系数时程曲线(风速：12 m/s)Fig.7 Drag and lift coefficient time-history curve of typical wind attack(wind speed:12 m/s)

通过模拟得到12 m/s风速下各风攻角的阻力系数和升力系数时程曲线，进而获得时程稳定后的阻力系数和升力系数的平均值，其随风攻角的变化规律(见图8)。平均阻力系数曲线呈两端低中间略高的形状，70°～100°风攻角的平均阻力系数波动相对比较大。平均升力系数曲线呈现“M”状，曲线两侧各有一尖峰，升力系数在0°、90°和180°风攻角处约为0，在20°风攻角时达到最大值1.0，在120°风攻角附近达到负峰值。

将图8中三维模拟的阻力系数和升力系数与二维模拟、风洞试验值相比较，三维模拟获得的平均阻力系数曲线处于二维模拟和风洞试验数据曲线的中间，略高于风洞试验数据曲线，对于平均升力系数而言，三维模拟的数据曲线与二维模拟、风洞试验相应数据曲线变化规律一致，均呈“M”状，但在风攻角60°～140°范围内，三维模拟的升力系数与风洞试验值接近，而二维模拟数据与风洞试验差别较大，三维比二维模拟更接近于试验值，三维模拟曲线比风洞试验曲线平缓。

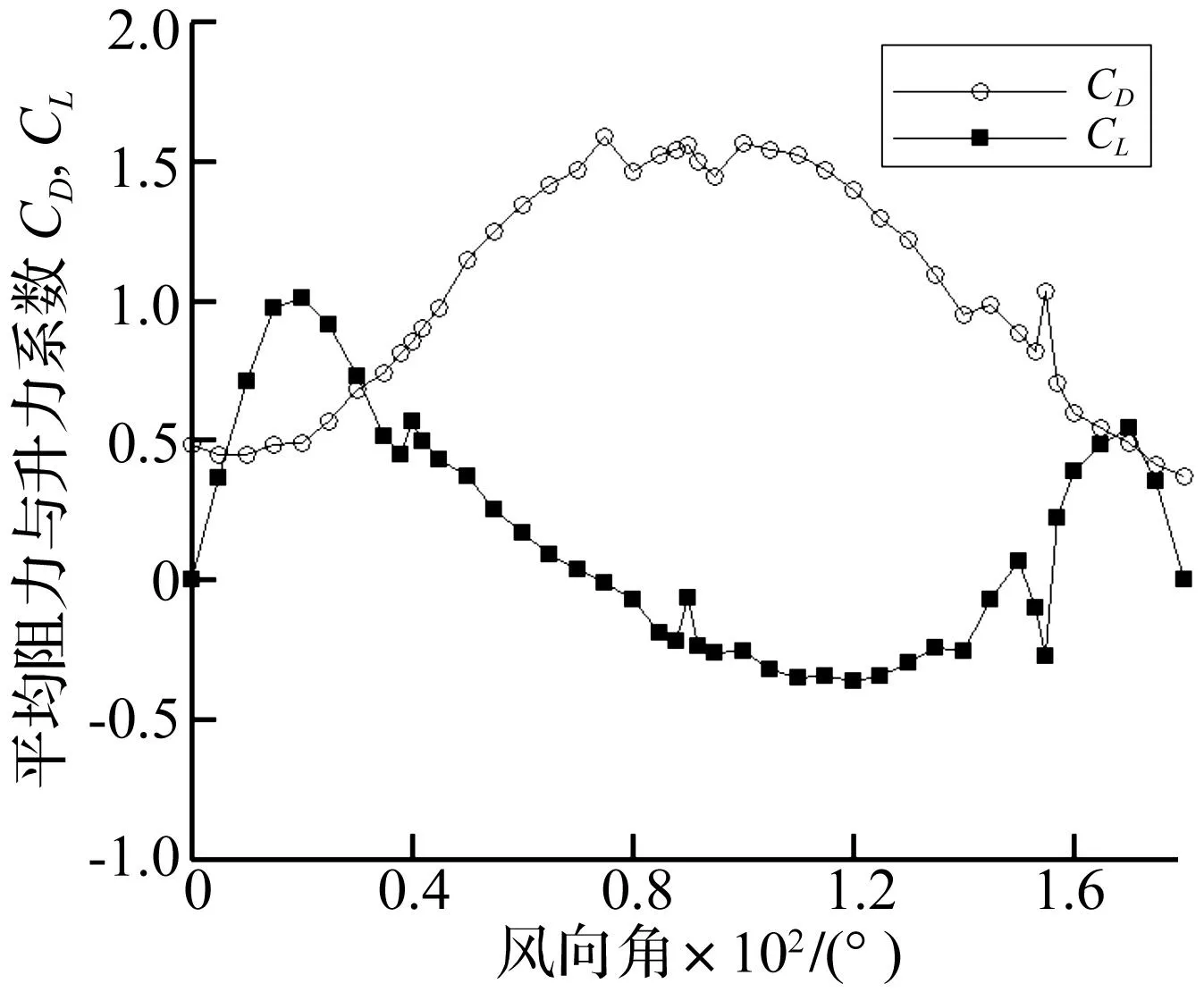
图8　三维模拟覆冰拉索气动力系数(风速：12 m/s)Fig.8 Aerodynamic coefficient of 3D simulation for iced cable(wind speed:12m/s)

3.3全攻角下三维覆冰拉索的驰振力系数

为了判断覆冰拉索发生驰振的可能性，运用式(3)计算可得到平均升力系数随风攻角变化曲线的斜率值与相应平均阻力系数的矢量和，即驰振力系数，但对于一个特定风攻角而言，∂CL/∂α可能取CL-α曲线的左侧曲线斜率或者右侧曲线斜率[15]。本文将两种情况下覆冰拉索随风攻角变化的驰振力系数列于图9中，当某风攻角处左侧曲线斜率和右侧曲线斜率分别对应的驰振力系数同时<0时，才认为拉索处于不稳定状态。从图9可知，在风攻角25°、30°、35°、42°、153°、175°处，两种情况的驰振力系数均出现负值，说明拉索处于不稳定状态，易发生覆冰驰振。

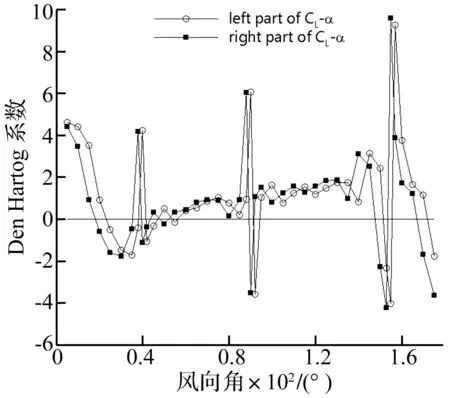
图9　三维模拟覆冰拉索驰振力系数(风速：12m/s)Fig.9 Galloping coefficient of 3D simulation for iced cable(wind speed:12m/s)

4覆冰斜拉索驰振临界风速

由于冬季华中地区空气湿度大，会出现雨雪边降边冻，导线和拉索极易受覆冰灾害的影响。本文则以某大跨斜拉桥为工程背景计算了拉索的驰振临界风速。表1给出了大跨斜拉桥部分斜拉索的结构参数[16]。

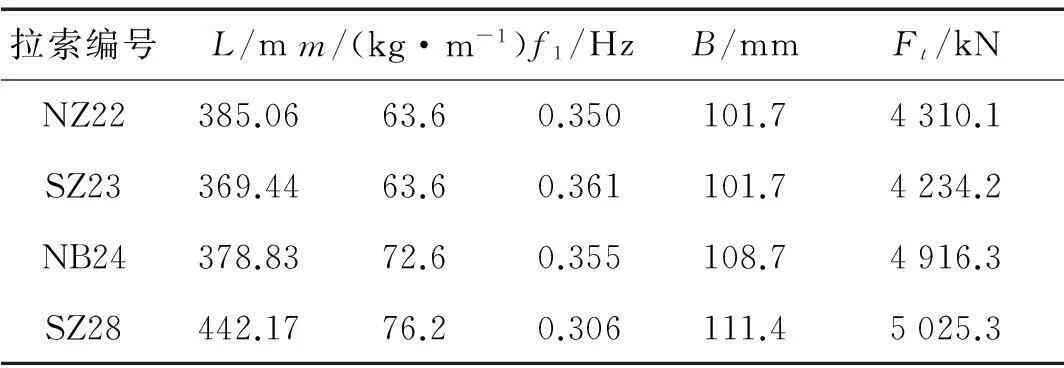
表1　某大跨斜拉桥斜拉索参数

由阻尼比1%及表中各参数，通过式(5)获得25°、30°、35°、42°、153°以及175°风攻角下各个覆冰斜拉索两种情况下的驰振临界风速，其数值见表2中(a)～(f)的数据。从表2可知在同一风攻角下，左侧曲线斜率和右侧曲线斜率分别对应的斜拉索驰振临界风速差别较大，在30°、153°、175°风攻角处，左侧曲线斜率和右侧曲线斜率分别对应的驰振临界风速均较小，最小临界风速仅有7.9 m/s，易发生覆冰驰振。覆冰斜拉索驰振临界风速随着质量和一阶频率的增大而增大，一般斜拉索长度越长，越容易发生覆冰驰振。

表2　覆冰斜拉索驰振临界风速

5结论

本文利用FLUENT软件对三维新月形覆冰斜拉索进行数值模拟，得到了覆冰拉索的气动力参数、驰振

力系数以及驰振临界风速，通过数值模拟结果分析得到如下结论：

(1) 文中监控截面的流场分布说明了空间拉索绕流场的三维流动特性，三维模拟比二维模拟更接近于实际流动。与风洞试验和二维模拟数据相比较，三维模拟得到的气动力系数随风攻角的变化规律比二维模拟更接近于风洞试验值。

(2) 三维模拟的新月形覆冰拉索在25°、30°、35°、42°、153°以及175°风攻角时左侧曲线斜率和右侧曲线斜率对应的驰振力系数均出现负值，拉索具有发生覆冰驰振的可能性。

(3) 以某大跨斜拉桥为工程背景，研究出其斜拉索在新月形覆冰条件下，30°、153°和175°风攻角的左侧曲线斜率和右侧曲线斜率分别对应的驰振临界风速均较小，最小临界风速仅有7.9 m/s，说明其斜拉索易发生覆冰驰振，一般拉索越长，驰振临界风速越小。

参 考 文 献

[ 1 ] Den Hartog J P. Transmission line vibration due to sleet[J]. Transactions of the American Institute of Electrical Engineers,1932,51:1074-1077.

[ 2 ] Nigol O,Buchan P G. Conductor galloping-Part Ⅱ:torsional mechanism[J]. IEEE Transactions on Power Apparatus and Systems,1981,100(2):708-720.

[ 3 ] 李万平. 覆冰导线群的动态气动力特性[J]. 空气动力学学报，2000，18(4)：414-420.

LI Wan-ping. Dynamic aerodynamic characteristicsof the galloping of bundled iced power transmission lines[J]. ACTA Aerodynamic Sinica,2000, 18(4):414-420.

[ 4 ] 李万平，黄河，何锃. 特大覆冰导线气动特性测试[J]. 华中科技大学学报，2001，29(8)：84-86.

LI Wan-ping,HUANG He,HE Zeng. Aerodynamic characteri-stics of heavilyiced conductors[J]. Journal of Huazhong University of Science and Technology, 2001,29(8):84-86.

[ 5 ] 严波，蔡萌琦，吕欣，等. 四分裂导线尾流驰振数值模拟研究[J]. 振动与冲击，2015，34(1)：182-189.

YAN Bo,CAI Meng-qi,LÜ Xin,et al.Numerical simulation on wake galloping of quad bundle conductor[J].Journal of Vibration and Shock,2015,34(1):182-189.

[ 6 ] 蔡萌琦，严波，吕欣，等. 覆冰四分裂导线空气动力系数数值模拟[J]. 振动与冲击，2013，32(5)：132-137.

CAI Meng-qi, YAN Bo, LÜ Xin,et al. Numerical investigation on aerodynamic coefficients of iced quad bundle conductor[J]. Journal of Vibration and Shock,2013,32(5):132-137.

[ 7 ] Braun A L,Awruch A M. Aerodynamic and aeroelastic analysis of bundled cables by numerical simulation[J]. Journal of Sound and Vibration,2005,51-73.

[ 8 ] 李寿英，黄韬，叶继红. 覆冰斜拉索驰振稳定性的理论研究[J]. 振动与冲击，2013，32(1)：122-127.

LI Shou-ying,HUANG Tao,YE Ji-hong. Theoretical analysis of galloping stability for stay cables with iced accretions[J].Journal of Vibration and Shock,2013,32(1):122-127.

[ 9 ] Demartino C,Ricciardelli F. Aerodynamic stability of ice-accreted bridge cables[J]. Journal of Fluids and Structures,2015,52:81-100.

[10] Demartino C,Koss H H,Georgakis C T, et al. Effects of ice ac-cretion on the aerodynamics of bridge cables[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015,138:98-119.

[11] 李寿英，黄韬，叶继红. 覆冰斜拉索气动力的试验与数值研究[J]. 湖南大学学报，2012，39(8)：1-6.

LI Shou-ying,HUANG Tao,YE Ji-hong. Experimental and numericalinvestigations of the aerodynamic forces on stay cables with iced accretion[J]. Journal of Hunan University,2012,39(8):1-6.

[12] Kravchenko A G, Moin P. Numerical studies of flow over a circular cylinder at ReD=3 900[J]. Physics of Fluids, 20 00, 12(2):403-417.

[13] 腾二甫，段忠东，张秀华. 新月形覆冰导线气动力特性的数值模拟[J]. 低温建筑技术，2008(1)：86-88.

TENG Er-fu,DUAN Zhong-dong,ZHANG Xiu-hua. Numerical simulations of aerodynamic characteristics of iced conductor with crescent shape[J]. Low Temperature Architecture Technology,2008(1):86-88.

[14] 陈政清. 桥梁风工程[M]. 北京：人民交通出版社，2005.

[15] 温晓光. 斜拉索干索驰振的机理研究[D]. 长沙：湖南大学，2013.

[16] 张武剑，王波，杨金保，等. 九江长江公路大桥斜拉索振动特性研究[J]. 世界桥梁，2012，40(6)：47-51.

ZHANG Wu-jian, WANG Bo,YANG Jin-bao,et al. Study of vibration property of stay cables of Jiujiang Changjiang river highway bridge[J]. World Bridges, 2012,40(6)：47-51.

Galloping analysis of wind-induced vibration for 3D stay cables with iced accretion

TANDong-mei1,WANGKai-li1,QUWei-lian1,HANLing2,GAOYuan-zhi1(1.School of Civil Engineering, Wuhan University of Technology, Wuhan 430072, China;2. Hubei Provincial Academy of Building Research and Design, Wuhan 430071, China)

Abstract:The stay cables with iced accretion have the off-centered cross section, and their aerodynamic shape is no longer stable. These may lead to their galloping vibration under the action of wind. A galloping vibration with a large amplitude threatens the security of stay cables, so it is necessary to analyze deeply the galloping stability of stay cables with iced accretion. Here, the flow field of 3D iced cables was simulated by applying SST k-ω model of FLUENT. The drag, lift and galloping force coefficients under the whole attack angle were computed to estimate the possibility of their gallop. The critical galloping wind speeds of part of stay cables of a certain cable-stayed bridge were obtained. The results showed that part of galloping force coefficients computed with 3D simulation of the iced cables are less than zero, and the critical galloping wind speeds are smaller, the stay cables are easy to gallop; compared with wind tunnel tests and 2D simulation data, the aerodynamic force parameters computed with 3D simulation of iced cables are more close to the test results than those computed with 2D simulation.

Key words:iced accretion; stay cables; aerodynamic force parameters; galloping; critical wind speed

中图分类号:U448.27

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.024

收稿日期：2015-01-27修改稿收到日期：2015-04-02

基金项目：国家自然科学基金资助项目(51408452)；国家重点实验室开放基金资助项目(2013B114)；中央高校基本科研业务费专项资金资助(2013-IV-035)

第一作者 谭冬梅 女，博士，副教授，1976年生