船舶-自升式海洋平台碰撞相似率研究

刘　昆， 包　杰,2， 王自力, Wang George,3

(1.江苏科技大学 船舶与海洋工程学院，江苏 镇江　212003; 2.上海船舶设计研究院，上海　200120；3.美国船级社，新加坡)



船舶-自升式海洋平台碰撞相似率研究

刘昆1， 包杰1,2， 王自力1, Wang George1,3

(1.江苏科技大学 船舶与海洋工程学院，江苏 镇江212003; 2.上海船舶设计研究院，上海200120；3.美国船级社，新加坡)

摘要：海洋平台作为海洋能源勘探开发的主要组成部分，是海洋油气探井、钻井、开采的主要作业基地,船舶碰撞致使平台结构损伤破坏一直是威胁海洋平台安全的主要因素之一，开展海洋平台碰撞性能研究，揭示平台结构在碰撞过程中的损伤变形机理，对提升平台安全性具有重要意义。评估平台结构耐撞性能最可靠的方法是实船碰撞试验，然而因其耗资巨大而不易开展。按一定相似关系进行比例模型试验成为现实条件下的首选。基于相似第二定理，运用量纲分析法推导船舶-自升式海洋平台碰撞过程中各物理量的相似关系，为平台碰撞模型试验的开展及试验参数的确定提供重要依据;结合有限元仿真技术，以平台典型的T型和K型管节点为研究对象，建立不同缩尺比下的简化碰撞模型，比较验证相似理论的可靠性;研究结果表明，缩尺模型在碰撞冲击载荷下的结构损伤变形、碰撞力和能量吸收等动态响应与实尺度模型结果一致性较好。研究成果可以为大型平台结构碰撞模型试验设计提供技术支撑。

关键词：船舶碰撞；相似关系；量纲分析；数值仿真；模型试验设计

海洋平台作为海洋能源勘探开发的主要组成部分，是海洋油气探井、钻井、开采的主要作业基地。由于平台周边海域通常会有船舶作业，或平台本身位于主要航道，使其遭受船舶碰撞的概率大大增加[1]，船舶碰撞致使平台结构损伤破坏一直是威胁海洋平台安全的主要因素之一。在各类海洋平台中，自升式平台以其较好的定位能力和作业稳定性在海洋油气开发勘探中占据主力地位，但其柔性较大，结构冗余度偏低，抵抗碰撞冲击的能力相对较弱。因此，在自升式平台结构设计阶段考虑结构的耐撞性能具有重要意义。

评估平台结构耐撞性能最可靠的方法是实船碰撞试验，然而因其耗资巨大而不易开展[2]。开展比例模型的碰撞试验可以为简化解析算法及数值仿真计算提供验证依据，也可以在一定程度上分析结构的耐撞性能。尽管相似原理在一些领域已有了一定程度的应用，但针对船舶与海洋平台结构碰撞这种动态强非线性问题，确定其相似准则仍较困难。相关的研究成果主要集中在运用量纲分析法推导结构发生大变形的相似率上。其中雷正保[3-4]以波金汉第二定理为基础，运用量纲矩阵法，将试验研究中的相似原理引入强非线性相似结构动态响应分析，导出了发生弹塑性大变形结构的动态相似准则。谢建林[5]根据相似理论分别推导了水下爆炸冲击波载荷相似率和弹塑性结构遭受水下爆炸冲击波载荷作用下的动响应相似率，并通过数值方法验证了相似率的正确性。Cho等[6]将相似理论运用于一系列管状支柱的动态冲击模型中，进行了近海半潜式风力涡轮机支撑结构与供给船碰撞的相似率研究。

本文基于相似第二定理，运用量纲分析法推导船舶-自升式海洋平台碰撞过程中各物理量的相似关系，采用数值仿真方法，以平台典型的T型和K型管节点为研究对象，建立不同缩尺比下的节点碰撞模型，比较验证相似理论的可靠性，研究成果可以为平台碰撞模型试验的开展及试验参数的确定提供重要依据。

1船舶-自升式海洋平台碰撞的相似理论分析

1.1量纲分析法

由于物理量是有量纲的，因此用数学方程来描述任何一个客观规律时，等式两边的量纲必须一致，称为量纲一致原则。在量纲一致的原则下，分析等式中物理量关系的方法称为量纲分析法。

美国科学家Buckingham提出了相似第二定理，该定理可表达为：设描述一物理现象的函数关系中包含n

个物理量，涉及到m个基础量纲，则该现象具有(n-m)个相似准则，且描述此现象的函数关系式可达成(n-m)个相似准则间的函数关系式。通过相似第二定理，可以把量纲分析法运用到研究相似现象和相似准则中，建立各物理量之间的函数关系，使定量研究成为可能。

1.2碰撞相关物理量

船舶碰撞是一个复杂的非线性动态响应过程，考虑到被撞平台的结构特点，在研究船舶-自升式海洋平台碰撞动态相似率时对撞击船和被撞平台做了适当的简化，本文重点研究被撞平台时将撞击船的球鼻艏简化为一刚性半球[7]，被撞平台简化为桩腿被撞处的管节点，该处理方案既可以简化计算，同时也可满足相似性研究的要求。

基于相似第二定理，运用量纲矩阵法推导碰撞过程的相似准则。本文仅考虑各向同性弹塑性材料且原型与模型取同种材料，相同边界条件，表征碰撞过程中结构动态响应这一现象的物理量分析如下：

1.3动态相似准则

根据∏定理可以得到以上15个物理量的无量纲一般∏项式为：

∏=Rsα1Msα2Vsα3tα4δα5(t)εα6(t)σα7(t)×

(1)

以力F、长度L和时间T的单位作为基本量纲，将各物理量的单位转化为基本量纲的形式，如σ(t)的单位Pa可转化为N/m2，写成量纲矩阵的形式(见表1)。

表1　系统的量纲矩阵

由于∏为无量纲数，单位的指数之和为零，故以表1中每行的数据为系数，建立关于各物理量指数的方程组：

α2+α7+α10+α11+α12+α13+α15=0

(2a)

α1-α2+α3+α5-2α7-2α10-

2α11+α12-4α13+α14-2α15=0

(2b)

2α2-α3+α4-α8+2α13=0

(2c)

表2为关于式(2)的∏矩阵，其中以α13、α14、α15为自变量，其他数为应变量，应用矩阵法求解物理量的指数方程得到12个无量纲∏数，即碰撞的动态相似准则，如式(3)所示：

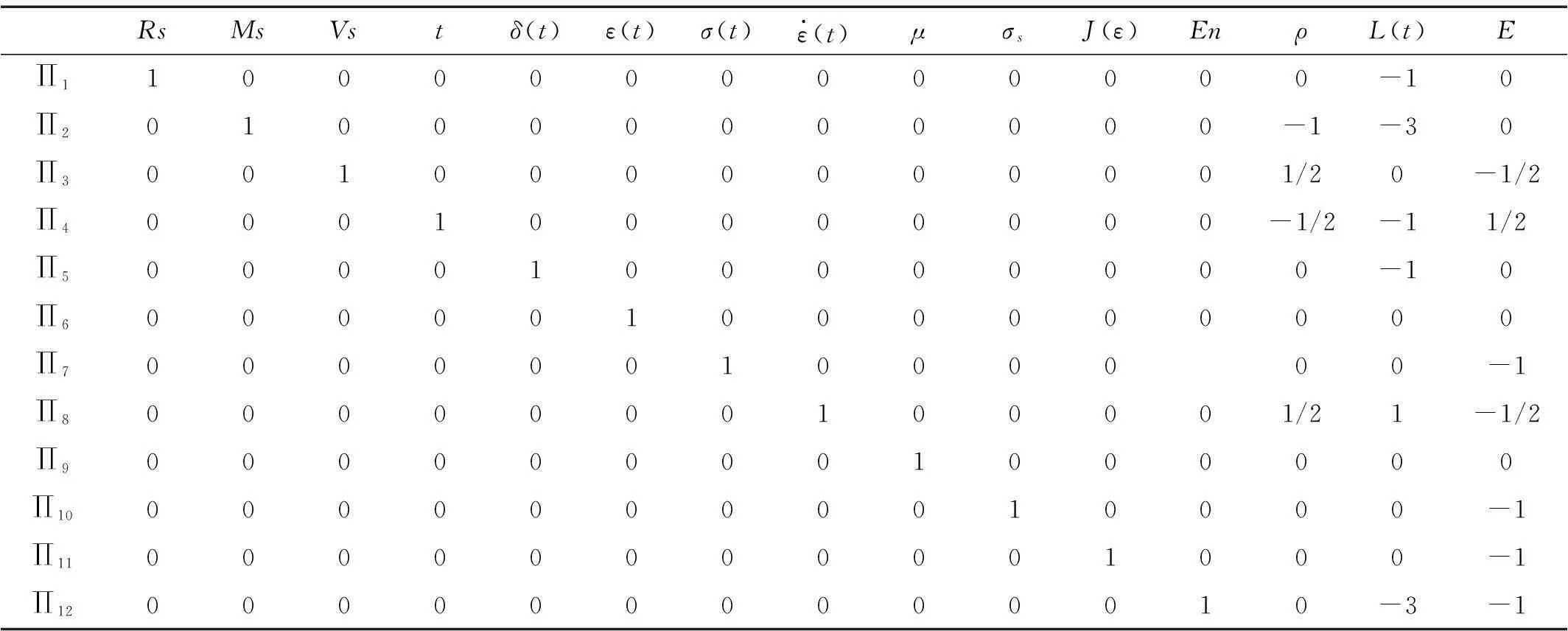
表2　系统的∏矩阵

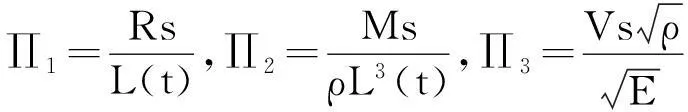
(3)

1.4碰撞物理量相似比

模型与原型采用相同材料，故有λρ=λE=λμ=λJ(ε)=λσs=1

式中：λ为模型与原型的相似比，下标为具体的物理量，如密度的相似比λρ是相似模型密度与原型密度的比值。

由于原型与缩尺模型遵循完全几何相似，将几何相似倍数λL(t)代入式(3)可得其余各参数的相似比尺：

λRs=λL(t)，λδ(t)=λL(t)

λMs=λ3L(t)，λVs=1

λEn=λ3L(t)，λσ(t)=λε(t)=λσs=1

通常λt取为常数，从而λL(t)也必为常数，此时t时刻的加速度相似倍数λa(t)以及碰撞力相似倍数λF(t)为：

λF(t)=λMsλa(t)=λ2

因此，在动态分析中，只要时间相似倍数λt取为常数，则在整个时间域中，相似系统的相似倍数均为常数。现可取t=0时刻的几何尺寸倍数作为基本参数，即λL(0)=λt=λ。此时，各物理量相似比尺见表3。

表3　船舶-自升式海洋平台碰撞各物理量相似比尺

尽管模型与原型取相同的材料，但并不是所有参数项均能满足相似理论[8]。由表3可得材料应变率按照相似理论应扩大为原来的λ-1倍，但由于材料对应变率是敏感的[9]，缩尺前后材料的强度发生了改变，材料的屈服应力及屈服点应变也不成比例关系，且随着相似比的减小影响越明显。因此，比例模型与原型的相似比应该控制在一个合理的范围内。

2船舶-自升式海洋平台碰撞相似率的数值验证

2.1有限元模型概况

参照相似率理论分析中的简化方法，选取船舶-海洋平台碰撞的典型场景进行数值仿真分析，将撞击船简化为刚性半球，被撞平台简化为桩腿水线以下的管节点，选取桩腿上的典型结构为碰撞区域，分别为弦杆与水平撑杆组成的T型管节点结构和弦杆与斜撑杆组成的K型管节点结构(见图1)。为简化问题，将T型与K型管节点弦管与撑杆边缘刚性约束，撞击船运动方向位于管节点平面，垂直于弦管方向，初速度大小为2 m/s。运用有限元软件ABAQUS建立不同缩尺比下T型、K型管节点结构碰撞模型，进行动态相似准则的有限元验证。原模型与缩尺模型的详细尺寸见表4，其中scale1、scale2、scale5和scale10模型分别对应缩尺比为1、2、5和10。

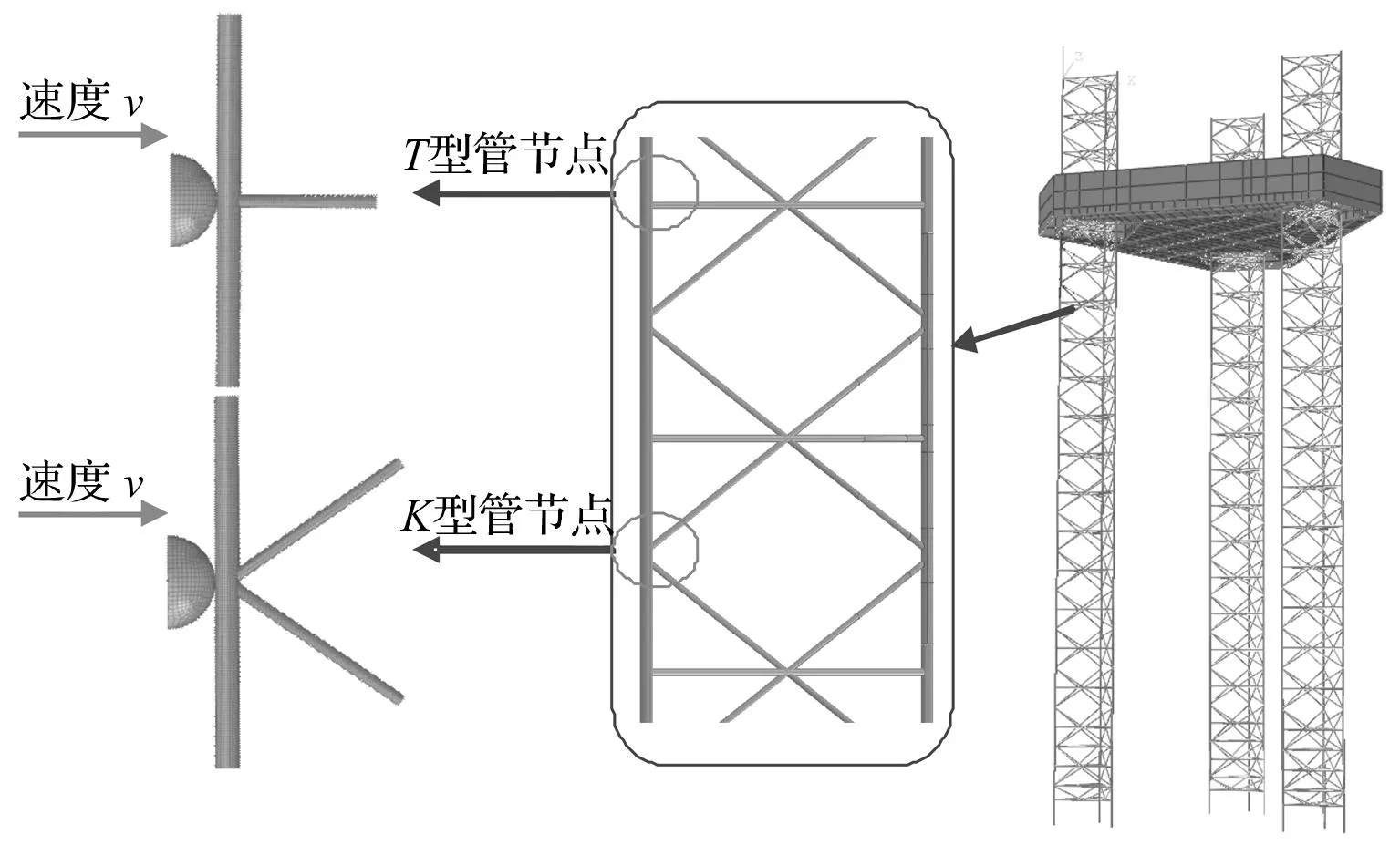
图1　碰撞有限元模型Fig.1 Finite element model

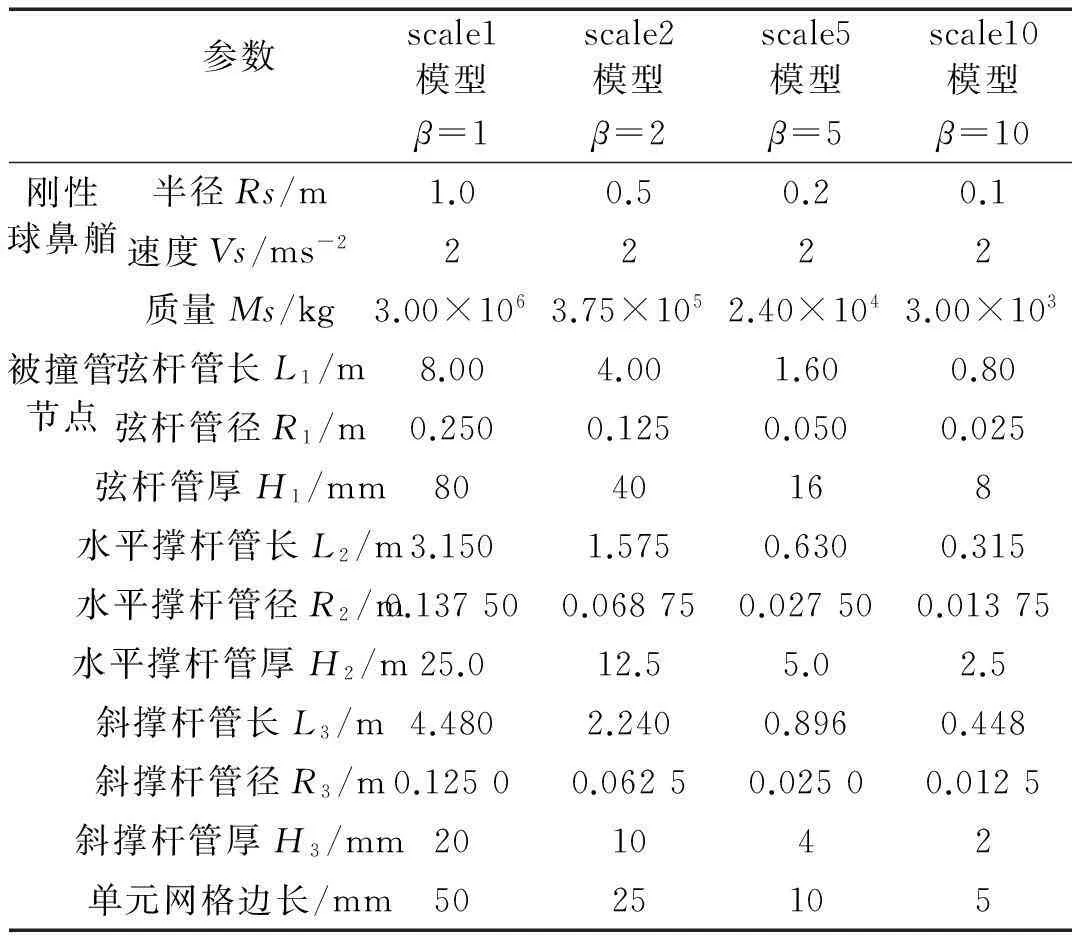
参数scale1模型scale2模型scale5模型scale10模型β=1β=2β=5β=10刚性球鼻艏半径Rs/m1.00.50.20.1速度Vs/ms-22222质量Ms/kg3.00×1063.75×1052.40×1043.00×103被撞管节点弦杆管长L1/m8.004.001.600.80弦杆管径R1/m0.2500.1250.0500.025弦杆管厚H1/mm8040168水平撑杆管长L2/m3.1501.5750.6300.315水平撑杆管径R2/m0.137500.068750.027500.01375水平撑杆管厚p/m25.012.55.02.5斜撑杆管长L3/m4.4802.2400.8960.448斜撑杆管径R3/m0.12500.06250.02500.0125斜撑杆管厚h1/mm201042单元网格边长/mm5025105

管节点模型材料采用船用低碳钢，其基础力学性能见表5，在材料模型中选用考虑应变率敏感性影响[9]的Cowper-Symonds本构方程，其参数D=40.4，q=5[10-12]。

表5　船用低碳钢的基本力学特性

2.2相似率在T型管节点上的运用与验证

将不同缩尺比下T型管节点碰撞模型提交计算，得到相应的动态响应过程。下面分别给出T型管节点结构的损伤变形，撞击船的位移、速度、加速度，碰撞力以及结构遭受碰撞冲击载荷后的吸能情况。将模型时历曲线中各点横坐标t按时间比尺放大，同时也将各纵坐标按各自的缩尺比放大即得相似等效后的时历曲线图。

2.2.1损伤变形

图2为不同缩尺比下T型管节点的应力和等效塑性云图。从图2可知，不同缩尺比的结构损伤变形模式基本一致，其中弦杆上发生了局部凹陷变形和整体弯曲变形的叠加，其上的最大应力和最大等效塑性应变均出现在跨中的碰撞区域，不同缩尺比下水平撑杆发生失稳弯曲变形的方向不同，应力集中的位置也有差别，这是由于杆件受压失稳方向的随机性所导致的。同时，四组模型的最大应力分别为502.6 MPa、533.5 MPa、557.6 MPa、563.2 MPa，最大塑性应变分别为0.469、0.460、0.458、0.458，其一致性较好。由此可见，在撞击速度不变的前提下，选取相同材料，按照完全几何相似进行缩尺建立模型，T型管节点结构内部的应力和塑性应变满足动态相似准则。

2.2.2各撞击参数的时历曲线

图3～图7给出了相似等效前后T型管节点碰撞模型中各碰撞参数的时历曲线图。从图中可以看出，相似等效前不同缩尺比的曲线横纵坐标均呈现出一定的比例关系，经过几何相似率等效后，不同缩尺比碰撞模型中的各时历曲线一致性较好。其中，位移曲线先增大后减小，结合速度曲线可知撞击船在与T型管节点相互作用的过程中先正向减速至速度为零，后由于管结构的弹性被反向弹开。加速度和碰撞力曲线则经历了线性急速上升、平稳和线性急速下降三个阶段，其中上升段为弹性变形阶段，稳定段为塑性变形阶段，下降段对应撞击船反向被弹开。结构所获得的变形能由撞击动能转化而来，随着撞击船速度的减小，撞深逐渐增加，弦杆与水平撑杆的吸能也随之提高，在0.52 s时撞深达到最大，结构总吸能也达到峰值。从以上图表中可知，取同种材料且满足完全几何相似条件时，用缩尺后的T型管结构模型来预测原结构受到碰撞冲击载荷时的动响应特征是较为准确可靠的。

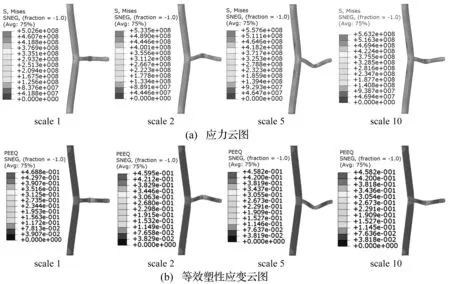
图2　T型管节点损伤变形情况Fig.2 Damage deformation of T type joints

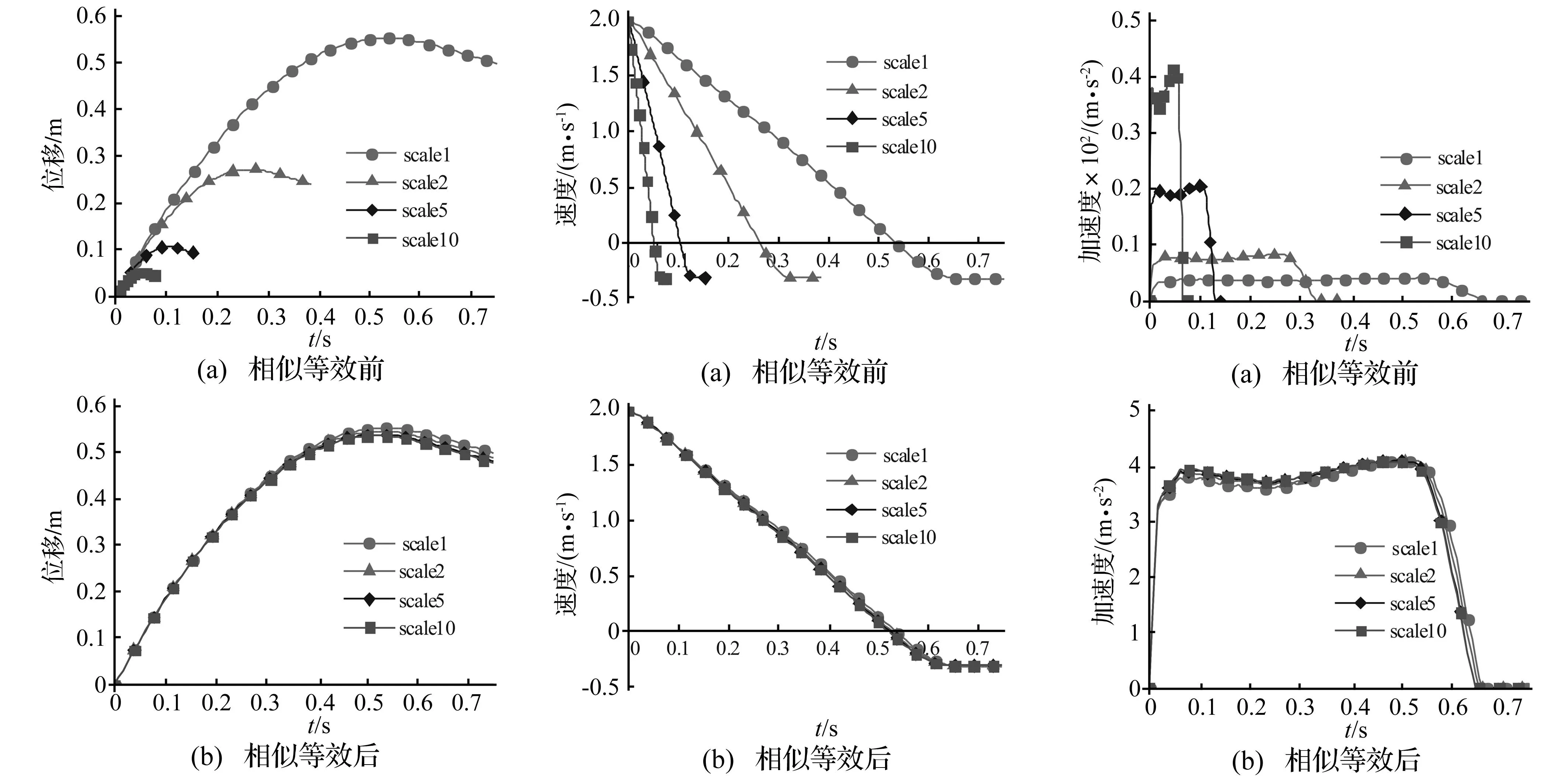
图3 撞击船的位移时历曲线图Fig.3Thedisplacement-timerelationshipsofstrikingship图4 撞击船的速度时历曲线图Fig.4Thevelocity-timerelationshipsofstrikingship图5 撞击船的加速度时历曲线图Fig.5TheAcceleration-timerelationshipsofstrikingship

2.3相似率在K型管节点上的运用与验证

将不同缩尺比K型管节点碰撞模型提交计算，得到相应的撞击响应过程。下面分别给出K型管节点结构的损伤变形，撞击船的位移、速度、加速度，碰撞力以及结构遭受碰撞冲击载荷后的变形吸能情况。

2.3.1损伤变形

图8为不同缩尺比下K型管节点的应力和等效塑性应变云图。从图8的应力应变的分布及数值上可知,与上文相似的结论即在撞击速度不变的前提下，选取同等材料，大变形动态相似准则在K型管节点碰撞模型上同样适用。

2.3.2各撞击参数的时历曲线

图9给出了相似等效后不同缩尺比K型管节点模型各碰撞参数的时历曲线图。从图9可知，经过几何相似率等效后，不同缩尺比碰撞模型中的各时历曲线一致性较好。因此无论在T型还是K型管节点结构中，相似准则均适用。

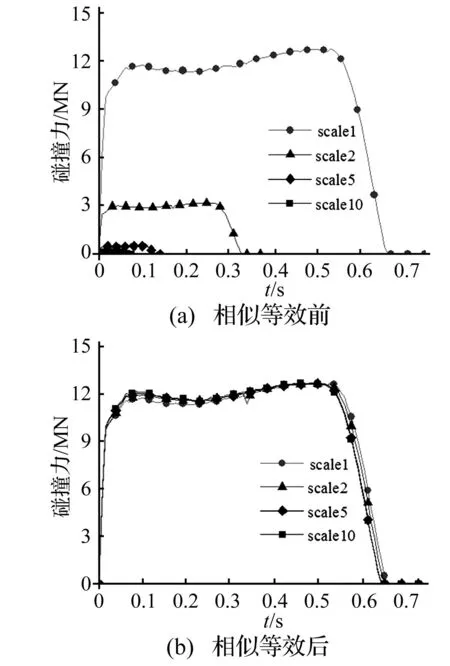
图6　碰撞力时历曲线图Fig.6 The collision force-time relationships

图7　T型管节点总吸能时历曲线图Fig.7 The total absorbing energy-time relationships of T type joints

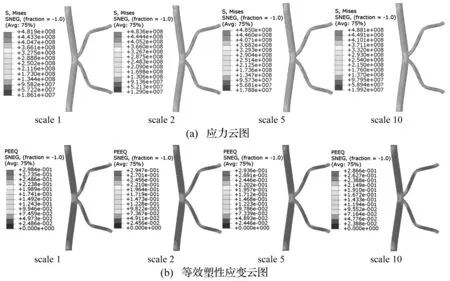
图8　K型管节点损伤变形情况Fig.8 Damage deformation of K type joints

2.4误差分析

为了更好地验证相似率的准确性，探求相似性研究中隐藏的规律，下面列出各缩尺比模型参数计算结果的峰值处偏差和平均偏差，详见表6。

定义偏差为：

图10给出了T型、K型管节点碰撞模型不同缩尺比下各参数偏差值的变化曲线。从图10可知,随着缩尺比的增大，缩尺模型与原型的偏差也相应增大，这是由于完全几何缩尺过程中一些物理现象如应变率敏感性、裂纹的扩展以及惯性现象等无法按照既定的相似准则来实现缩尺，且缩尺比越大误差越明显，故小尺度模型试验的精度往往难以保证。但从图中曲线的最大值可知缩尺模型的峰值偏差和平均偏差均控制在<10%，满足模型试验的精度要求，因此当缩尺比选取在一个合适的范围内时，所造成的误差较小，此时可以通过缩尺模型来表征原碰撞结构的动态响应过程。此外，

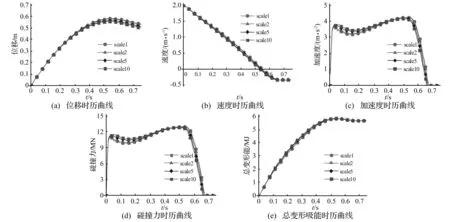
图9　相似等效后各碰撞参数的时历曲线图Fig.9 The various impact parameters-time relationships after similarity equivalence

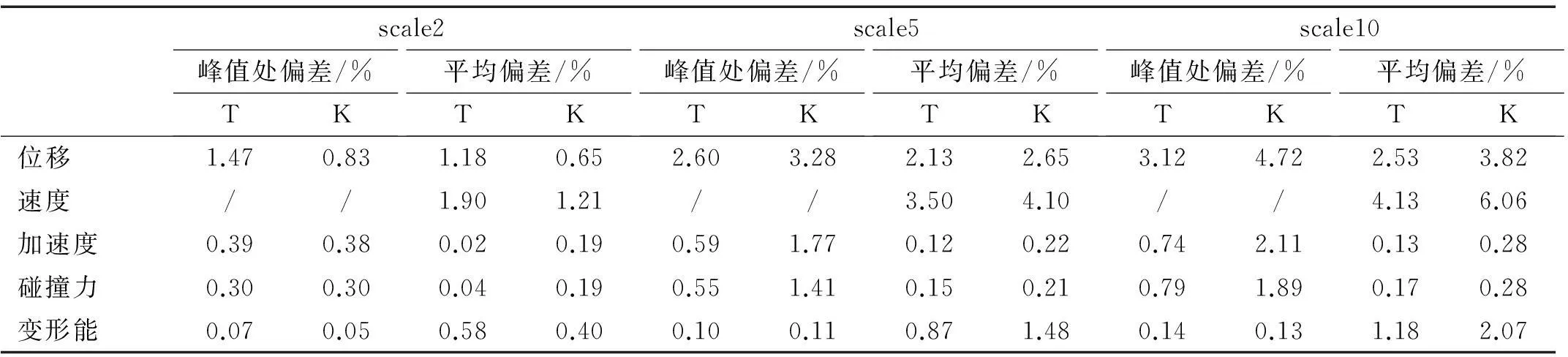
scale2scale5scale10峰值处偏差/%TK平均偏差/%TK峰值处偏差/%TK平均偏差/%TK峰值处偏差/%TK平均偏差/%TK位移1.470.831.180.652.603.282.132.653.124.722.533.82速度//1.901.21//3.504.10//4.136.06加速度0.390.380.020.190.591.770.120.220.742.110.130.28碰撞力0.300.300.040.190.551.410.150.210.791.890.170.28变形能0.070.050.580.400.100.110.871.480.140.131.182.07

通过比较T型与K型管节点各参数偏差值随缩尺比变化关系可以发现，当缩尺比取较小数值时两种结构由缩尺引起的偏差比较接近，但随着缩尺比的增大两组曲线的斜率有所区别，其中K型结构偏差曲线较T型增长快，较大缩尺下偏差明显高于T型结构，这是因为T型结构组成上较K型简单，其影响缩尺的因素也较少，但总体偏差均在可以接受的范围内。

3结论

本文基于量纲分析方法推导了船舶-自升式海洋平台碰撞的相似准则，同时采用数值仿真方法对碰撞的相似准则进行了仿真计算与验证。主要结论如下：

(1) 运用量纲矩阵法，结合船舶-自升式海洋平台碰撞场景，选取碰撞相关物理量推导出适用于碰撞冲击类问题的动态相似准则，所列出的相关物理量相似比尺可为相关碰撞模型试验方案的制定提供参考。

(2) 通过仿真计算了不同缩尺比下自升式海洋平台T型、K型管节点的碰撞性能，发现两种结构在碰撞过程中的动态响应均满足相似率，且产生的误差也在工程允许的范围之内，故将动态相似率运用于船舶-自升式海洋平台碰撞相似性研究中具有较好的适用性与准确性。

参 考 文 献

[ 1 ] Amdahl J. Collision between platform deck and service vessel wheelhouse[D]. Trondheim:Norwegian University of Science and Technology,2007.

[ 2 ] 温小飞，卢金树，崔振东. 船舶碰撞过程的数值模拟及试验研究[J]. 浙江海洋学院学报:自然科学版,2011,30(1):71-76.

WEN Xiao-fei, LU Jin-shu, CUI Zhen-dong. Numerical simulation and experiment research of ship collision process[J]. Journal of Zhejiang Ocean University:National Science,2011,30(1):71-76.

[ 3 ] 雷正保. 汽车结构的大变形动态相似准则及相似计算精度[J]. 实验力学,2000,15(4):429-435.

LEI Zheng-bao. Dynamic similarity criteria for automotive structures of elastic-plastic materials under large deformation condition and precision of similarity calculation[J].Journal of Experimental Mechanics, 2000,15(4):429-435.

[ 4 ] 雷正保. 大位移大转角弹塑性相似结构的相似比[J]. 机械工程学报,1999,35(2):6-9.

LEI Zheng-bao. Similitude ratios of elastic-plastic similitude structure with large displacements and large deformations for dynamic system[J].Chinese Journal of Mechanics Engineering,1999,35(2):6-9.

[ 5 ] 谢建林. 瞬态载荷作用下弹塑性结构动响应相似性研究[D]. 哈尔滨:哈尔滨工程大学,2008.

[ 6 ] Cho S R, Seo B S. Experimental and numerical investigations on the collision between offshore wind turbine support structures and service vessel[J]. Collision and Grounding of Ships and Offshore Structures,2013,49:281-287.

[ 7 ] 刘昆,张延昌,王自力. 船首形状对舷侧结构碰撞性能影响研究[J]. 船舶工程,2010,32(2):12-14.

LIU Kun, ZHANG Yan-chang, WANG Zi-li. Study on the influence of bow shape to the side structure during ship collision[J]. Ship Engineering,2010,32(2):12-14.

[ 8 ] 张维俊. 船舶结构碰撞相似律的数值研究[J]. 中国舰船研究,2009,4(3):38-41.

ZHANG Wei-jun. Numerical simulation research of ship collision analogue rule[J].Chinese Journal of Ship Research,2009,4(3):38-41.

[ 9 ] Liu K, Wang Z L, Tang W Y, et al. Experimental and numerical analysis of laterally impacted stiffened plates considering the effect of strain rate[J]. Ocean Engineering,2015,99:44-54.

[10] 王自力,顾永宁. 应变率敏感性对船体结构碰撞性能的影响[J]. 上海交通大学报,2000,34(12):1704-1707.

WANG Zi-li, GU Yong-ning. Effect of strain-rate sensitivity on the behavior of ship structure in collision[J].Journal of Shanghai Jiaotong University, 2000,34(12):1704-1707.

[11] 王自力,蒋志勇,顾永宁. 船舶碰撞数值仿真的附加质量模型[J]. 爆炸与冲击,2002,22(4):321-326.

WANG Zi-li, JIANG Zhi-yong, GU Yong-ning. An added water mass model for numerical simulation of ship/ship collisions[J]. Explosion and Shock Waves, 2002,22(4):321-326.

[12] Travanca J, Hao H. Dynamics of steel offshore platforms under ship impact[J]. Applied Ocean Research,2014,47:352-372.

[13] Oshieo R E, Alves M. Predicting the behavior of structures under impact loads using geometrically distorted scaled models[J]. Journal of the Mechanics and Physics of Solids,2012,60:1330-1349.

[14] Oshieo R E, Alves M. Scaling of cylindrical shells under axial impact[J]. International Journal of Impact Engineering,2007,34:89-103.

Scale model tests with a similarity ratio during collision between ship and offshore Jack-up platform

LIUKun1,BAOJie1,2,WANGZi-li1,WANGGeorge1,3(1. School of Naval Architecture and Ocean Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China;2. Shanghai Merchant Ship Design and Research Institute, Shanghai 201200, China; 3. American Bureau of Shipping, Singapore)

Abstract:An offshore platform is one of the major means for offshore exploration, it is the main operating base for exploratory well, drilling and mining of offshore oil and gas. However, ship collision is a major risk to their safety. It is very important to understand structural behavior of an offshore platform subjected to ship collision. Full-scale ship collision test is the most reliable method to evaluate the collision resistance of a platform structure. But it is too expensive to be affordable. Therefore, a scale model test with a similarity ratio may be a good choice in reality. Based on the second similarity theory, the dimensional analysis was used to derive the similar relations among the various physical quantities during a ship-offshore jack-up platform collision, and to provide important data for the collision model tests and determining test parameters. Combined with finite element simulation technique, taking typical T type and K type joints in a platform as the study objects, simplified collision models were built in different scales to compare and verify the reliability of the similarity theory. The results showed that the dynamic responses, such as, structural damage deformation, collision force and energy absorption of scale models under impact load agree well with those of prototypes. The study results provided technical supports for collision model test design of large platform structures.

Key words:ship collision; similarity ratio; dimensional analysis; numerical simulation; model test

中图分类号:P751

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.07.003

通信作者王自力 男，博士，教授，1964年生

收稿日期：2015-07-07修改稿收到日期：2015-09-08

基金项目：国家自然科学基金(51379093)

第一作者 刘昆 男，博士，讲师，1984年生