基于模糊PI永磁同步电机优化矢量控制系统的研究

樊英杰，张开如，马慧，韩璐，狄东照（山东科技大学电气与自动化工程学院，山东青岛266590）

转矩方程和运动方程为



基于模糊PI永磁同步电机优化矢量控制系统的研究

樊英杰，张开如，马慧，韩璐，狄东照
（山东科技大学电气与自动化工程学院，山东青岛266590）

摘要：介绍了永磁同步电机（PMSM）的数学模型和基本原理。针对PMSM中传统PI控制器参数固定、无法兼顾静态性能和动态性能的缺陷性，在传统双闭环控制策略的基础上，将速度外环采用模糊PI控制器，在线调整PI控制器的2个参数，增强系统的鲁棒性。逆变器环节采用优化SVPWM算法，该方法利用电压空间矢量旋转的幅角来判断扇区，并由三相电压的电压差值计算基本电压矢量的作用时间，与传统SVPWM相比简化了矢量算法步骤。仿真结果和小波分析表明，模糊PI优化矢量控制系统与传统PI矢量控制系统相比具有更好的动态稳定性和抗干扰能力。

关键词：永磁同步电机；速度外环；模糊PI控制；逆变器；优化SVPWM；小波分析

永磁同步电机（PMSM）以其体积小、效率高、功率密度大而得到了广泛的应用，特别是国内永磁材料的发展使得PMSM应用更加广泛［1］。随着应用场合的多样化，对动态和静态性能的要求也越来越高［2］。但PMSM系统在运行过程中定子电阻和负载可能会发生很大变化，这些参数变化会影响系统的动态响应和控制精度。因此以往的一些控制算法，如传统PI矢量控制策略难以满足要求［3］，所以获得更加有效的控制策略成为目前PMSM控制领域研究的热点。

目前常用的模糊控制方法有模糊PI控制、自适应模糊控制、神经模糊控制、遗传优化算法的模糊控制、专家模糊控制等［4］。PMSM传统控制方法主要是基于PI的速度电流双闭环控制，而单纯的PI控制本质是一种线性控制方式，满足不了控制精度的要求，抗干扰能力较差［5］。因此传统PI控制器无法从根本上解决动态性能和静态性能之间的矛盾［6］。考虑到双闭环控制系统的性能主要由外环决定，在速度外环将模糊控制器与PI控制器相结合，将速度偏差e和偏差微分量de作为输入［7］。利用模糊控制器对PI控制器中的2个参数在线调整，使模糊PI控制器既具有模糊控制灵活适应性强的优点，也具有PI控制精度高的优点，从而使模糊PI控制器中参数的整定值达到全局最优［8］。逆变器环节的调制方法主要有载波调制法（SPWM）和电压空间矢量（SVPWM）调制法，输出性能取决于调制方法［9］。传统SVPWM算法涉及到坐标变换，大量的三角函数计算，其算法复杂、运算量大［10］。非正交坐标系下的SVPWM算法减少了三角函数的运算，但仍然涉及到复杂的坐标变换问题［11］。论文提出的优化SVPWM算法利用合成电压空间矢量旋转过的幅角判断电压矢量所在的扇区，每个扇区内用相电压的差值计算基本矢量的作用时间。其模型简单，步骤清晰，更有利于数字化实现。

本文首先介绍了PMSM数学模型，在传统双闭环PI矢量控制策略的基础上，速度外环改为模糊PI控制，逆变器环节采用优化SVPWM算法。并对模糊PI控制器的设计原理以及优化SVPWM算法进行分析。最后通过仿真和小波分析验证了该模型具有良好的动静态性能。

1　永磁同步电机（PMSM）数学模型

忽略磁路不饱和、磁滞损耗、涡流等影响因素，PMSM在d-q坐标系下的电压方程为

磁链方程为

转矩方程和运动方程为

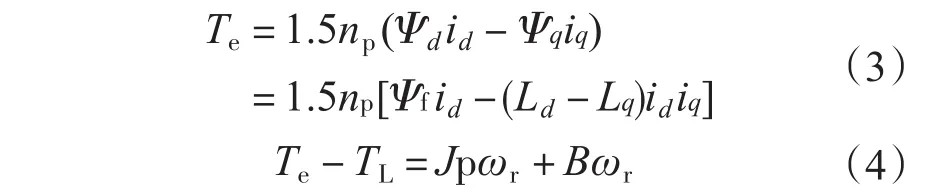
式中：vd,vq为d轴和q轴的定子电压；id,iq为d轴和q轴的定子电流；Rs为定子电阻；Ψf为转子磁链；p为微分算子；ωr为转子角频率；Ψd,Ψq为d轴和q轴的定子磁链；Ld,Lq为d轴和q轴电感；Te,TL为电磁转矩和负载转矩；np为磁极对数；J,B分别为电机转动惯量和摩擦及风阻力矩系数。

从式（1）中可以看出在d-q坐标系下两相之间相互耦合，故电压方程是非线性的。因此采用简单线性PI控制不能体现PMSM的非线性本质，使系统的控制性能受到限制。PMSM矢量控制原理图见图1。

图1　PMSM矢量控制原理图Fig.1 Vector control principle diagram of PMSM

2　模糊PI控制器设计

模糊控制器是以模糊集合、模糊语言变量和模糊规则推理为基础的智能控制方法。模糊PI控制系统如图2所示。

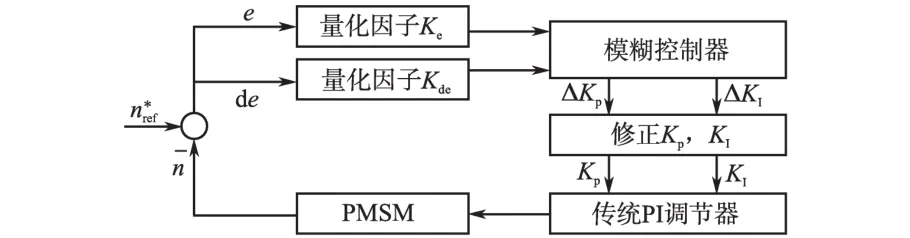
图2　模糊PI控制系统Fig.2 Control system of fuzzy PI

图2中，偏差e和偏差微分量de：

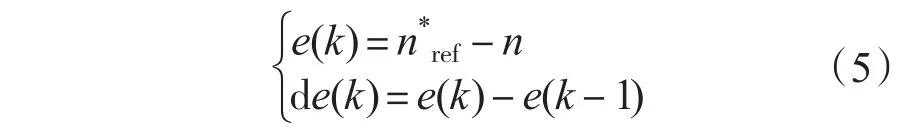
e,de分别经过量化因子Ke,Kde输入二维模糊控制器。模糊控制器输出量PI控制器的增量ΔKP,ΔKI，在线调整PI控制器中的参数KP,KI：

式中：KPO,KIO分别为PI控制器中比例系数和积分系数的初始值。

通过实时控制KP,KI使系统的PI参数值达到全局最优。

e(k),de(k),ΔKP,ΔKI的隶属函数如图3所示。

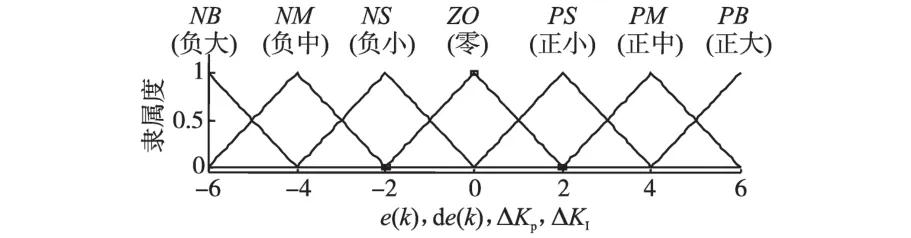
图3　e(k),de(k),ΔKP,ΔKI的隶属函数Fig.3 Membership function of e(k),de(k),ΔKP,and ΔKI

图3中e(k),de(k),ΔKP,ΔKI，各含7个模糊子集{NB，NM，NS，ZO，PS，PM，PB}，子集中的元素分别表示负大、负中、负小、零、正小、正中、正大，连续性论为［-6，6］。模糊化和去模糊化均采用三角形隶属函数，去模糊化采用加权平均法。模糊规则是模糊控制器的核心，通过分析和大量的实验仿真得到ΔKP,ΔKI的控制规则表，如表1、表2所示。

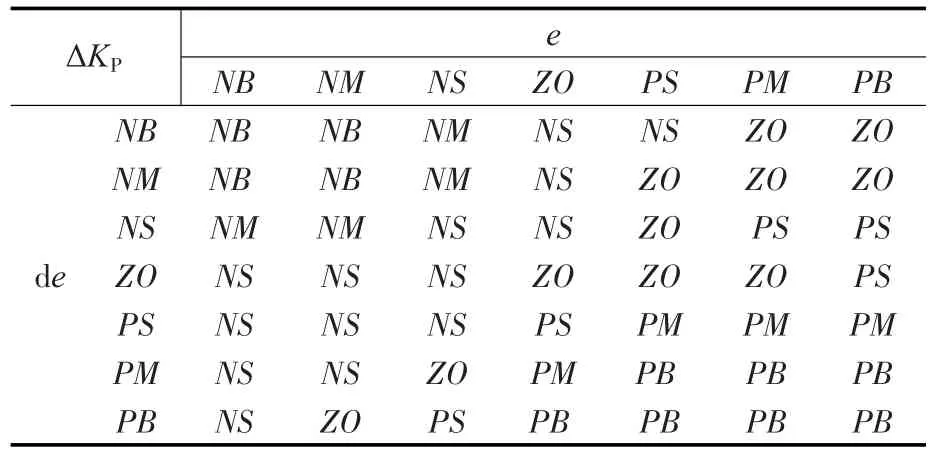
表1　ΔKP的模糊推理规则表Tab.1 Fuzzy inferential rules of ΔKP

表2　ΔKI的模糊推理规则表Tab.2 Fuzzy inferential rules of ΔKI

通过以上模糊规则可得模糊控制器输入输出的3D效果图，如图4所示。

从图4中可以看出模糊控制器根据输入量来输出ΔKP,ΔKI进而调整PI调节器中的比例积分系数，使PMSM在不同的速度范围都具有良好的动态和稳态性能。

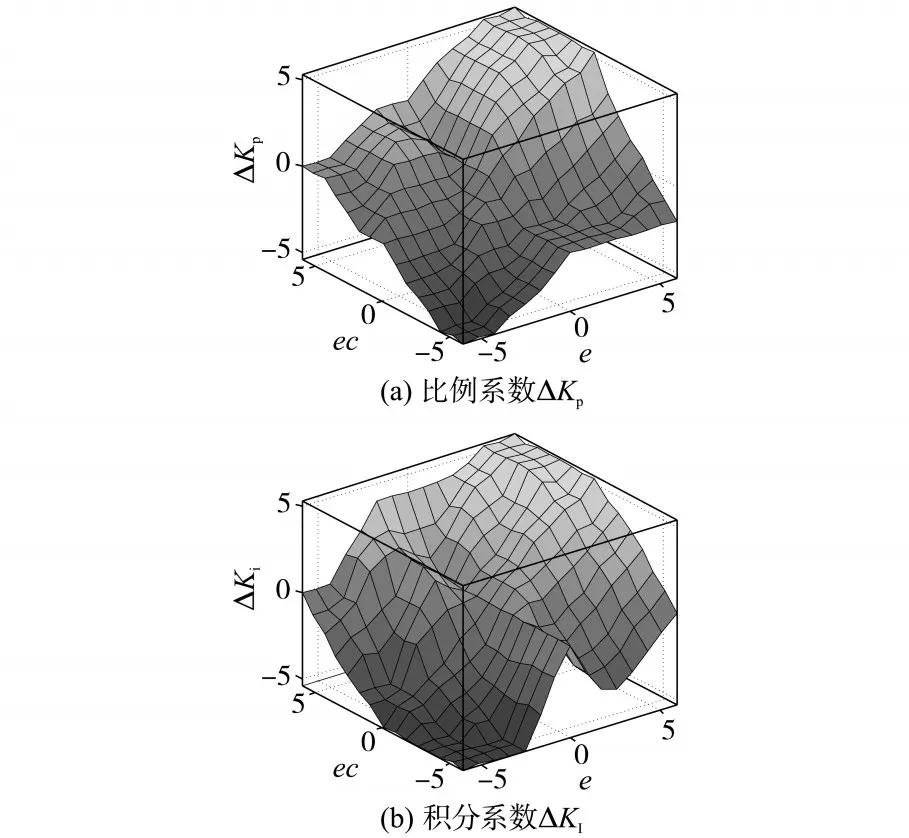
图4　模糊控制器的输入输出关系Fig.4 Relationship of the output and input for fuzzy controller

3　优化SVPWM算法

电压空间矢量图如图5所示。

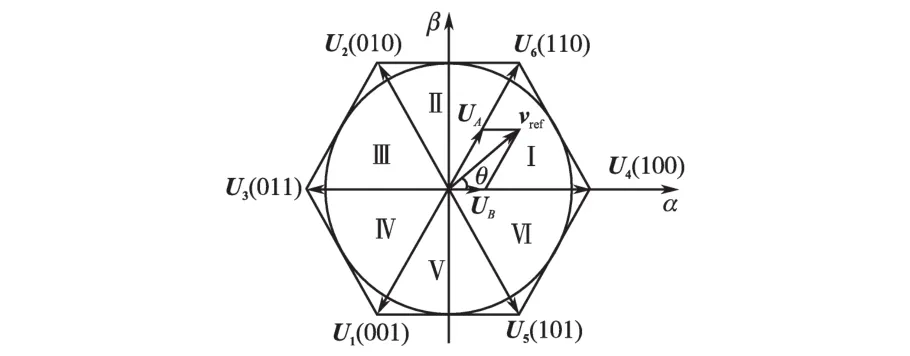
图5　电压空间矢量图Fig.5 Voltage space vector diagram

图5中，传统SVPWM算法复杂的根本原因是6个非零矢量中除U3（011），U4（100）外，其他非零矢量均不在α-β坐标轴上，无法用α-β坐标轴直接表示，因此造成基于α-β坐标系下算法过程不可避免的涉及到大量的三角函数运算。在图1中将输入逆变器的经过Clark-1变换：

即可得到静止坐标系下的三相电压va,vb,vc。定义三相正弦电压为

式中：Vm为峰值电压。

三相电压合成的空间电压矢量vref可以表示为

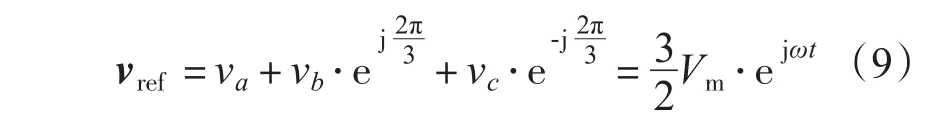
再由欧拉公式，得：

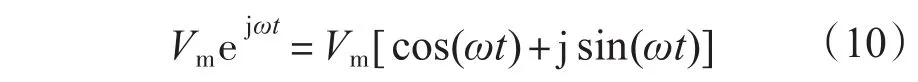
由复数的几何意义可知，vref为幅值恒定并以一定角频率ω进行逆时针旋转的矢量，其中|vref|=3Vm/2，ωt=θ。即幅角θ的变化率为角频率ω，因此可以通过幅角θ来判断vref所在的位置，θ取值范围为[-π,π]，采用3θ/π向上取整的方式来计算扇区。定义：

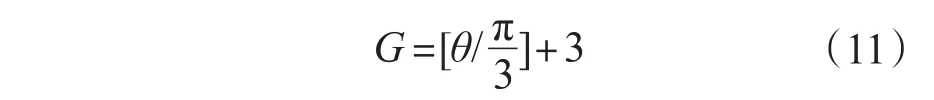
式中：G表示与扇区的对应关系；θ为vref与α轴之间的夹角。

当vref位于第I扇区时，设θ=π/6，则由式（11）可得G=4。因此通过式（11）可以求得G与扇区的对应关系，如表3所示。

表3　G与扇区的对应关系Tab.3 Relation of G and sectors

下面来计算基本电压矢量作用时间，如图3所示。以vref处在第I扇区时进行分析，根据伏秒平衡原则有：

式中：Tx,Ty为2个非零电压矢量的作用时间；Ts为开关周期。

由正弦定理：

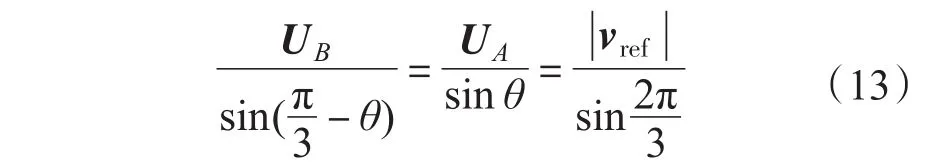
其中

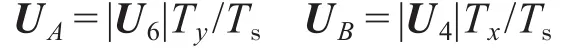
可以解得：

将a,b两相相减：

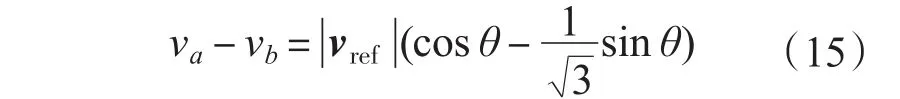
其中

由式（15）得：

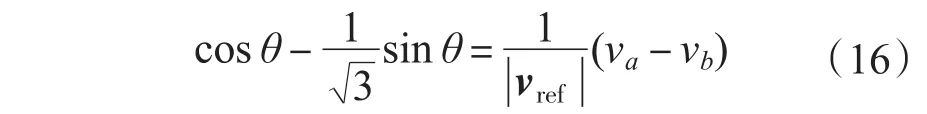
同理b,c两相的电压差为

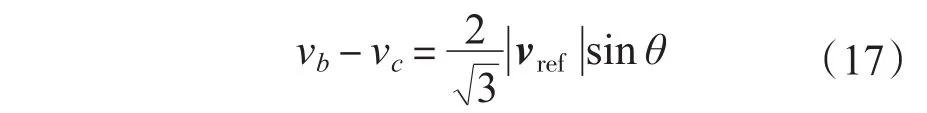
由式（17）可得：

将式（18）展开可得：

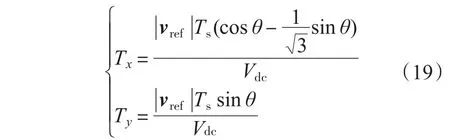
将式（16）、式（18）代入式（19），可得：

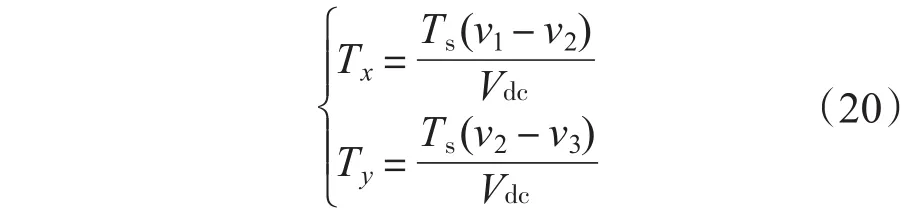
其中v1＞v2＞v3，由此可见非零矢量的作用时间只与每一扇区内三相相电压差值有关，因此只需知道每一扇区相电压之间的大小关系即可得到其他扇区非零矢量的作用时间。根据7段式SVPWM，在1个周期内3个上桥臂动作的时刻分别为Taon,Tbon,Tcon：

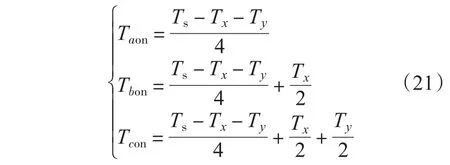
由以上推导可知，非零矢量的作用时间只需要加减运算即可获得，因此可根据式（20）、式（21）判断出每一扇区3个桥臂的动作时间。

4　仿真结果

采用Matlab/Simulink搭建模糊PI优化矢量控制系统和传统双闭环控制系统仿真模型。仿真中采用的表贴式永磁同步电机的参数为：定子电阻Rs=2.875 Ω；直轴电感和交轴电感Ld=Lq= 0.0085mH；转子磁链Ψf=0.175 Wb；电动机转动惯量J=0.0008kg·m2；粘滞摩擦系数B=0.001kg·m2/s；磁极对数np=4；负载转矩TL=2 N·m；图6所示采用优化SVPWM算法产生的调制波，与传统SVPWM算法产生的调制波相同，均为马鞍形的正弦波，即用更简单的算法达到相同的效果，同时验证了优化SVPWM的正确性。

图6　优化SVPWM调制波波形Fig.6 Modulation waveform of optimized SVPWM

转矩波形如图7所示。当PMSM稳定运行后，在0.5 s时突加负载TL由2 N·m变为4 N·m，电磁转矩响应迅速。

图7　转矩波形Fig.7 Torque waveform

图8所示为在两种不同的策略下转速波形的动态过程对比。模糊PI优化矢量控制策略与传统PI矢量控制策略相比，其转速提前40 ms达到稳态值，相当于2个基波的周期，具有更好的动态性能和更小的超调量。图9所示为在0.5 s时突加负载转矩，模糊PI优化矢量控制策略输出的转速波形在0.5 s时刻出现轻小波动，并很快恢复。而传统PI矢量控制策略输出的转速波形波动较大，并在0.75 s时刻再次到达稳定状态。

图8　转速波形Fig.8 Speed waveform

图9　突加转矩时转速波动波形Fig.9 Speed waveform when loading torque

图10　转速分布柱状图Fig.10 Distribution histogram of speed

为进一步对比两种系统的性能，论文选取具有良好紧支性、对称性和消失矩的sym8小波并进行4层分解，使其在提取波形信息的同时又保证有合适的消失距和快速的算法。图10为两种模型的转速波形分布柱状图，转速在稳态值1 200 r/min附近所占百分比较大，说明转速出现较大波动。模糊PI控制系统输出转速在稳态值1 200 r/min附近所占的百分小，说明转速的波动细微，因此模糊PI优化矢量控制系统具有更好的稳定性和抗干扰能力。

5　结论

永磁同步电机（PMSM）具有非线性、强耦合的特点，因此单纯使用PI控制器难以达到理想的控制效果。本文设计了模糊PI控制器，实时调整PI控制器中的参数。逆变器环节采用优化SVPWM算法，该方法避免了坐标变换，三角函数运算等过程，步骤清晰算法简单，仿真结果验证了该算法的有效性。

最后通过仿真结果及小波分析表明，模糊PI优化矢量控制策略与传统PI矢量控制策略相比，具有响应更快、鲁棒性强及运行更加稳定的特点。

参考文献

［1］张洪帅，王平，韩邦成.基于模糊PI模型参考自适应的高速永磁同步电机转子位置检测［J］.中国电机工程学报，2014，34（12）：1889-1896.

［2］鲁文其，胡育文，梁骄雁，等.永磁同步电机伺服系统抗扰动自适应控制［J］.中国电机工程学报，2011，31（3）：75-81.

［3］陈家伟，陈杰，陈冉，等.变速风力发电机组自适应模糊控制技术［J］.中国电机工程学报，2011，31（21）：93-101.

［4］辛斌，陈杰，彭志红.智能优化控制：概述与展望［J］.自动化学报，2013，39（11）：1831-1848.

［5］王永富，柴天佑.自适应模糊控制理论的研究综述［J］.控制工程，2006，13（3）：193-198.

［6］王述彦，师宇，冯忠绪.基于模糊PID控制器的控制方法研究［J］.机械科学与技术，2011，30（1）：166-172.

［7］朱颍合，薛凌云，黄伟.基于自组织调整因子的模糊PID控制器设计［J］.系统仿真学报，2011，23（12）：2732-2737.

［8］陆华才，徐月同，杨伟民，等.永磁直线同步电机进给系统模糊PID控制［J］.电工技术学报，2007，22（4）：59-63.

［9］杨贵杰，孙力，崔乃政，等.空间矢量脉宽调制方法的研究［J］.中国电机工程学报，2001，21（5）：79-83.

［10］刘焉.基于非正交坐标系下的SVPWM改进算法研究［J］.化工自动化及仪表，2010，37（1）：63-65.

［11］何罡，杨耕，窦曰轩.基于非标准正交基的空间电压矢量快速算法［J］.电力电子技术，2003，37（6）：1-3.

修改稿日期：2015-09-08

Study of Permanent Magnet Synchronous Motors Optimized Vector Control System Based on Fuzzy PI Controller

FAN Yingjie，ZHANG Kairu，MA Hui，HAN Lu，DI Dongzhao
（College of Electrical Engineering and Automation，Shandong University of Science and Technology，Qingdao 266590，Shandong，China）

Abstract:The mathematical model and the basic principle of permanent magnet synchronous motors were presented. Focusing on the defects of traditional PI controller of PMSM-fixed parameter making it unable to satisfy both static and dynamic performance，based on the traditional double-closed loop strategy，proposed to employ fuzzy PI controller for outer speed loop，which could adjust two parameters of PI controller on line and improve the robustness. An optimized SVPWM was applied to inverter，by which the sector could be judged according to the rotating argument of voltage space vector，and the function time of basic voltage vector could be calculated based on the 3 phase voltage difference computation and the algorithm steps were more simplified compared with the conventional SVPWM. The simulation results and wavelet analysis show that the fuzzy PI optimized vector system is superior the conventional PI vector control system in dynamic stability and anti-interference performance.

Key words:permanent magnet synchronous motors（PMSM）；outer speed loop；fuzzy PID control；inverter；optimized SVPWM；wavelet analysis

收稿日期：2015-04-18

作者简介：樊英杰（1990-），男，硕士研究生，Email：770650635@qq.com

中图分类号：TM341

文献标识码：A