有界控制导弹攻击防御性飞机的制导律

花文华，孟庆龄，张金鹏,2，张拥军

（1.中国空空导弹研究院，洛阳 471009；2.航空制导武器航空科技重点实验室，洛阳 471009）

有界控制导弹攻击防御性飞机的制导律

花文华1，孟庆龄1，张金鹏1,2，张拥军1

（1.中国空空导弹研究院，洛阳 471009；2.航空制导武器航空科技重点实验室，洛阳 471009）

为提高攻击导弹同时面对目标飞机及其防御导弹情况下的命中概率，基于微分对策理论，对攻击导弹的制导律进行了设计。应对独立控制的多对象博弈问题，微分对策理论具有天然的优势，且相比于最优制导律，微分对策制导律对于目标机动估计误差和机动策略具有更强的鲁棒性。所推导的微分对策制导律进一步考虑了攻击导弹的控制有界性，且适用于攻击导弹、目标飞机和防御导弹具有高阶线性控制系统动态的情形。为验证制导律性能，进行了非线性系统仿真，结果表明该制导律在成功归避防御导弹的同时可实现趋于零脱靶量的目标拦截。攻击导弹为实现规避和攻击的双重任务，仅需要保持相比于防御导弹两倍左右的机动优势。

制导律；微分对策制导；有界控制导弹；目标拦截

近年来出现了一类对飞机发射防御导弹协同防御来袭的攻击导弹问题的研究，并取得了一些成果[1-6]。如果这些思路在导弹工业中得以实现，将对攻击导弹的杀伤性能产生重要影响。

本文同样针对攻击导弹、飞机和防御导弹三方博弈问题进行研究，但着重于对攻击导弹同时面对防御导弹和飞机的情况进行制导律的设计。该制导律的推导从一般意义上展开，不受限于三方控制系统动态的约束，且考虑到攻击导弹的控制有界性。

1 问题描述及建模

制导末端的相对运动关系如图1所示，X轴沿初始视线方向，下标m、d和t分别对应攻击导弹、防御导弹和飞机的相关状态，且下标的组合形式表示相对状态，如mty 和dmy 分别表示攻击导弹和飞机间、防御导弹和攻击导弹间相对于X方向的位移。

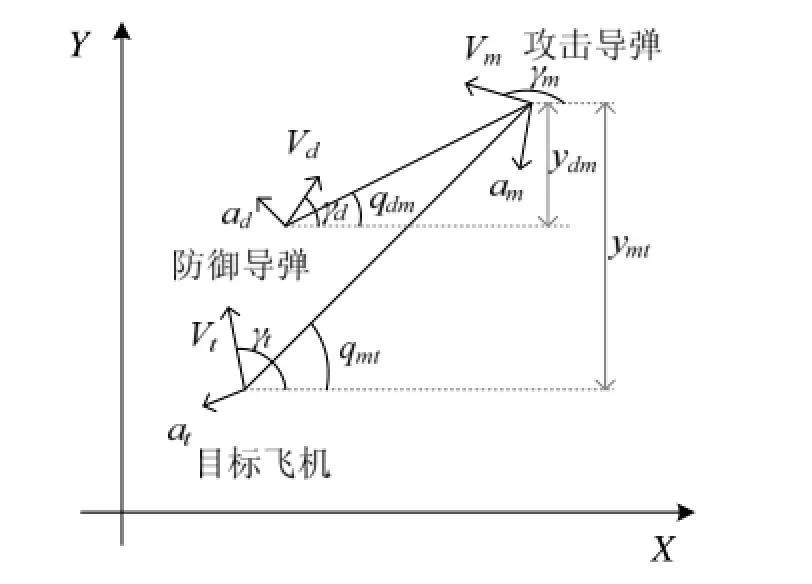
图1 平面相对运动关系Fig.1 Relative in-plane motion relationship

基于下述对攻击导弹、防御导弹和飞机的假设进行问题的分析：

1）三方相对运动关系可沿X方向进行线性化，速度大小保持不变，控制有界；

2）三方具有线性控制系统动态，且满足最小相位特性。

基于图1和上述假设，攻击导弹、防御导弹和飞机间的相对运动关系可近似表示为

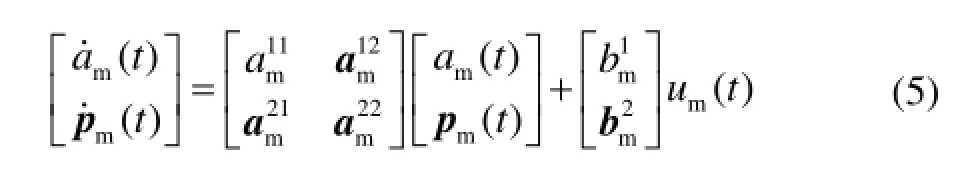
参考上述建模方式，防御导弹和飞机的控制系统模型表示为

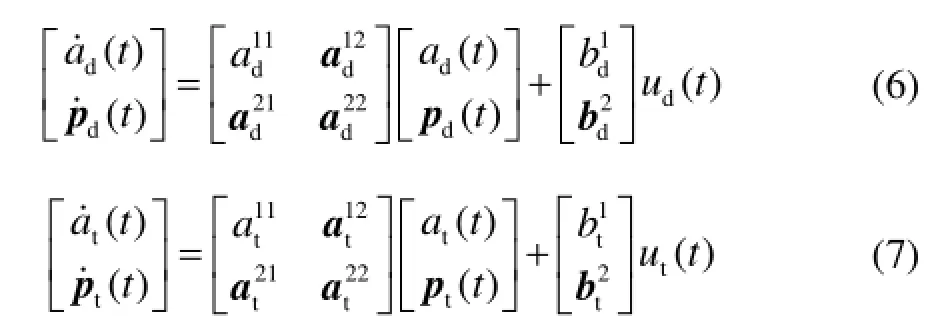
在式(6)和式(7)中，防御导弹和飞机的控制系统阶数分别为和为相应的控制命令。选取状态变量：

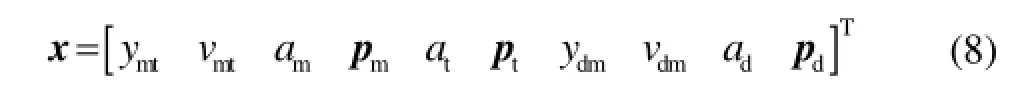
则整个系统的状态方程可表示为

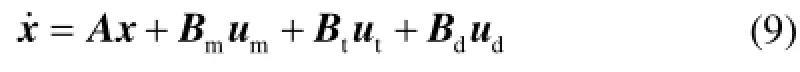
式中：

攻击导弹、飞机和防御导弹在实际情况下必然是控制有界的，定义三方的控制界值分别为

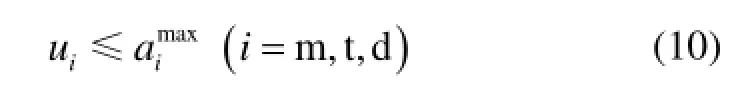
基于线性二次型性能指标所设计的制导律可以实现全弹道控制能量的最小化，但并未考虑到实际情况下导弹的有界控制性，从而制导末端较强的机动性能要求往往会带来较大的脱靶量，而在制导律的设计过程中就考虑到控制有界，因此可以获得较好的制导性能，文献[7-9]在该方面的研究较为深入。

基于假设(1)，攻击导弹与防御导弹的飞行时间为

2 制导律推导

2.1 微分对策制导律推导

定义性能指标：

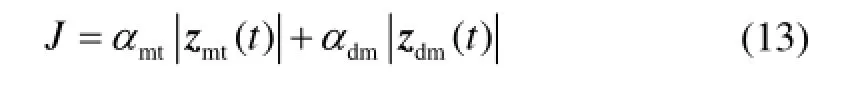
式中：mt>0α ，dm0α ＜ ，mtz 和dmz 分别表示攻击导弹和防御导弹的零控脱靶量[6,10]。基于微分对策理论，该性能指标以防御导弹脱靶量最大化和攻击导弹脱靶量最小化为设计目的，属于一类极大极小化设计问题。

针对性能指标(13)，直接进行制导律的推导会涉及到终端条件已知的 Riccati 微分方程组的求解，由于系统阶数较高，很难获得解析解。参考文献[11]采用零控脱靶量作为新的状态变量，首先降低系统维度，再进行制导律的推导。求解式(9)所对应的齐次方程，可以得到：

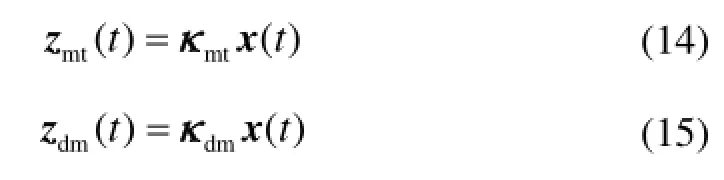
式(14)和式(15)中：

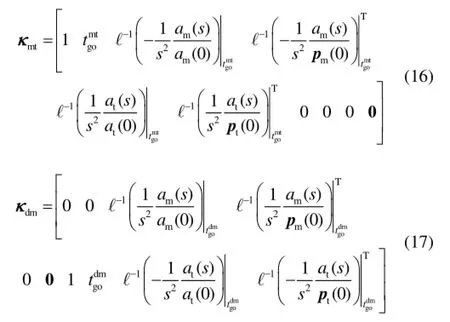
ℓ-1表示拉氏反变换。

对式(14)和式(15)两边求导，并经进一步整理，可以得到：

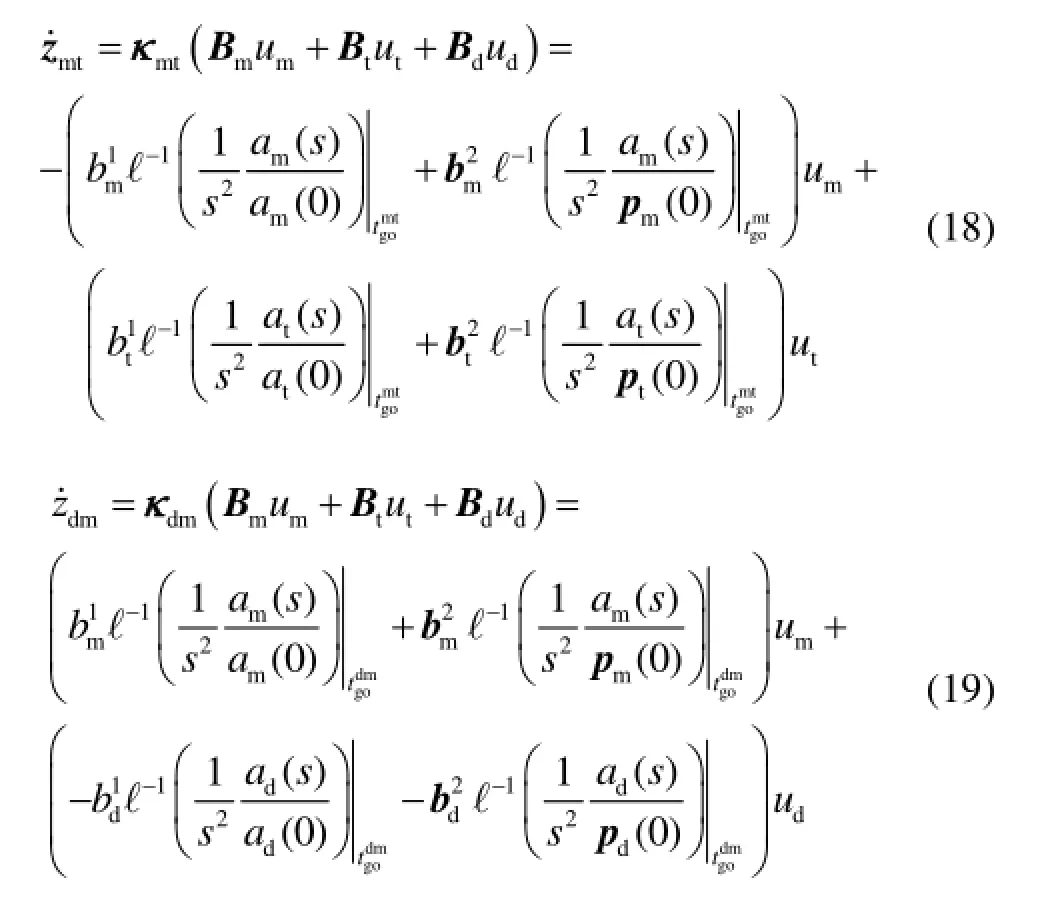
由式(18)和式(19)，构造哈密顿函数Η，并经进一步整理：

式中：dmλ 和mtλ 表示待定的拉格朗日乘子。进一步结合协态方程和横截条件可以求得：

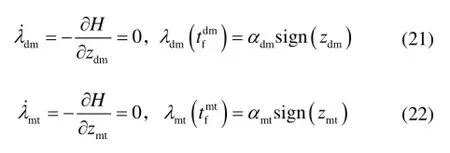
由于假设拦截导弹和目标的控制系统具有最小相位特性，其斜坡响应是单调增加的[12]，满足：

因此，基于上述推导和假设，攻击导弹、飞机和防御导弹具有一般形式的最优制导策略，可以表示为

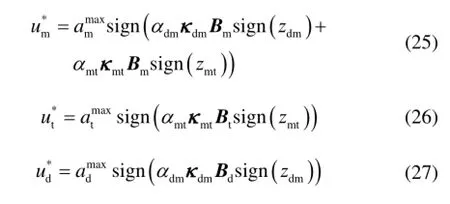
基于微分对策理论，推导了这一三方博弈问题的极大极小值解。式(25)即为攻击导弹攻击防御性飞行器的一般形式微分对策制导律，可适用于攻击导弹、飞机和防御导弹具有高阶控制系统动态的情形；而式(26)和式(27)也分别构成了飞机和防御导弹的最优规避策略和拦截策略。由设计过程可以发现，攻击导弹需要具备同时跟踪飞机和攻击导弹的能力，这一点对于日益成熟的导引头设计技术是逐步可以实现的，如将相控阵雷达设计技术应用到导引头的设计当中。

2.2 典型制导律

上文是从一般意义上进行攻击导弹制导律的推导，对攻击导弹、防御导弹和飞机的控制系统阶数并不加以约束。参考文献[10][13]，假设攻击导弹、防御导弹和飞机都近似具有一阶控制系统动态，且时间常数分别为mτ 、dτ和tτ，则系统状态转化为

由此状态向量并参考式(9)建立系统状态方程。经进一步代入计算，与制导律相关的参量可表示为

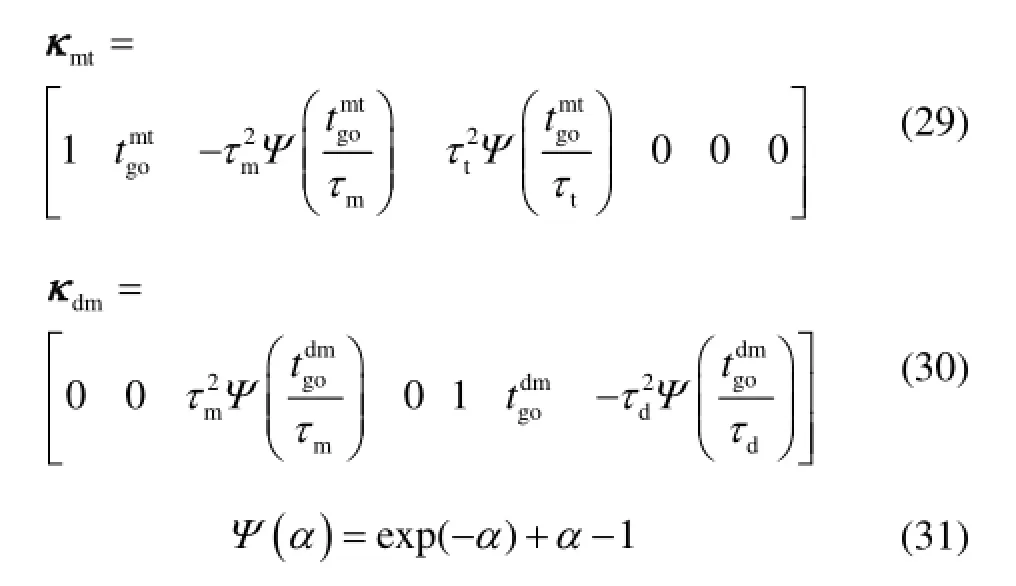
式(25)~(27)所示的攻击导弹、飞机和防御导弹的制导律可以表示为

若取可以得到：

式(35)所示的制导律与文献[5]的推导结果是类似的，但相比较而言，本文的推导过程更为简单，且结果更具有一般性。防御导弹虽然可以通过滤波方式对攻击导弹的制导律和制导参数进行估计[14]，从而优化自身的制导策略，但与攻击导弹制导律的式(32)恰好吻合的概率很小，甚至接近于零。

3 仿真结果及分析

针对平面非线性相对运动情形所推导的攻击导弹微分对策制导律进行了验证，仿真参数如表1所示，图2~5为仿真结果。仿真中假设防御导弹采用比例导引进行攻击导弹的拦截，而飞机做具有一次时间切换的“bang-bang”类型的机动[10]。的情况下，在攻击目标飞机的同时规避防御导弹的飞行弹道和剩余飞行时间。从图2中可以看出，防御导弹的脱靶量较大，主要原因是攻击导弹利用防御导弹的相关

图 2为攻击导弹最大机动性能信息主动规避机动，打破了防御导弹企图构建的拦截三角形（由预测拦截点、防御导弹和攻击导弹三点构建），从而摆脱其拦截，并随后切换到对飞机的攻击当中。攻击导弹的最终飞行时间为 6.305 s，脱靶量为0.074 9 m。图3和图4为分别取和情况下的飞行弹道和剩余飞行时间。随着攻击导弹最大机动性能的增加，攻击导弹飞行弹道更趋于平直，在规避防御导弹后的计算剩余飞行时间也更接近线性。两种情况的飞行时间分别为5.762 s和5.650 s，相应的脱靶量为 0.0657 m 和 0.0586 m。图 5为取10g = 情况下的飞行弹道，攻击导弹与防御导弹的最大机动性能基本相当。从图5中可以看出，攻击导弹虽然较飞机机动优势明显，但在规避防御导弹的拦截后，则要飞行更长的时间完成弹道的进一步调整才能命中飞机，因此对于存在防御导弹的情形，攻击导弹仍需要保持足够的机动性能优势。

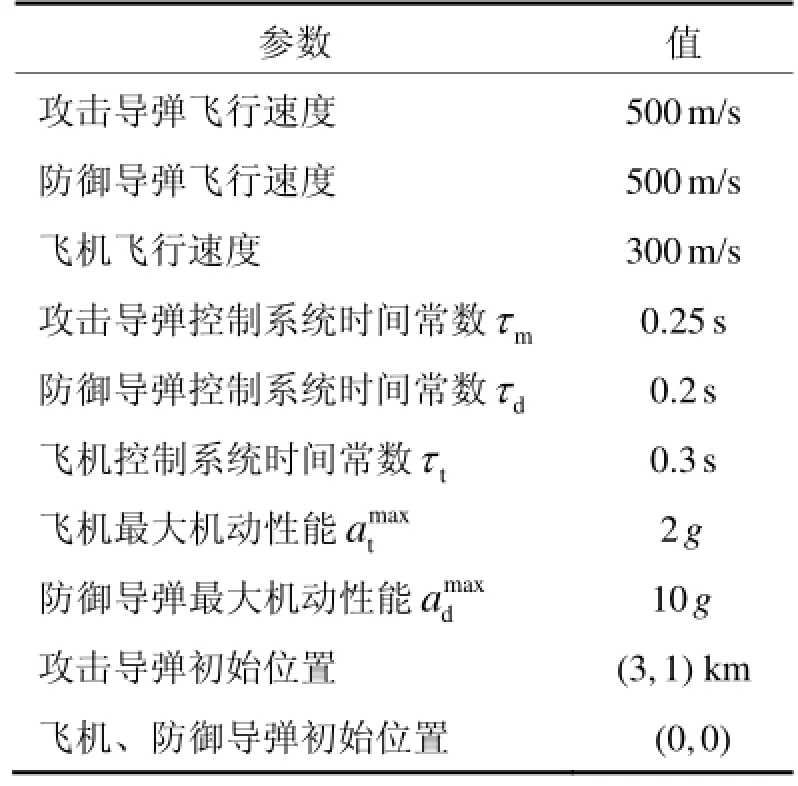
表1 仿真参数Tab.1 Simulation parameters

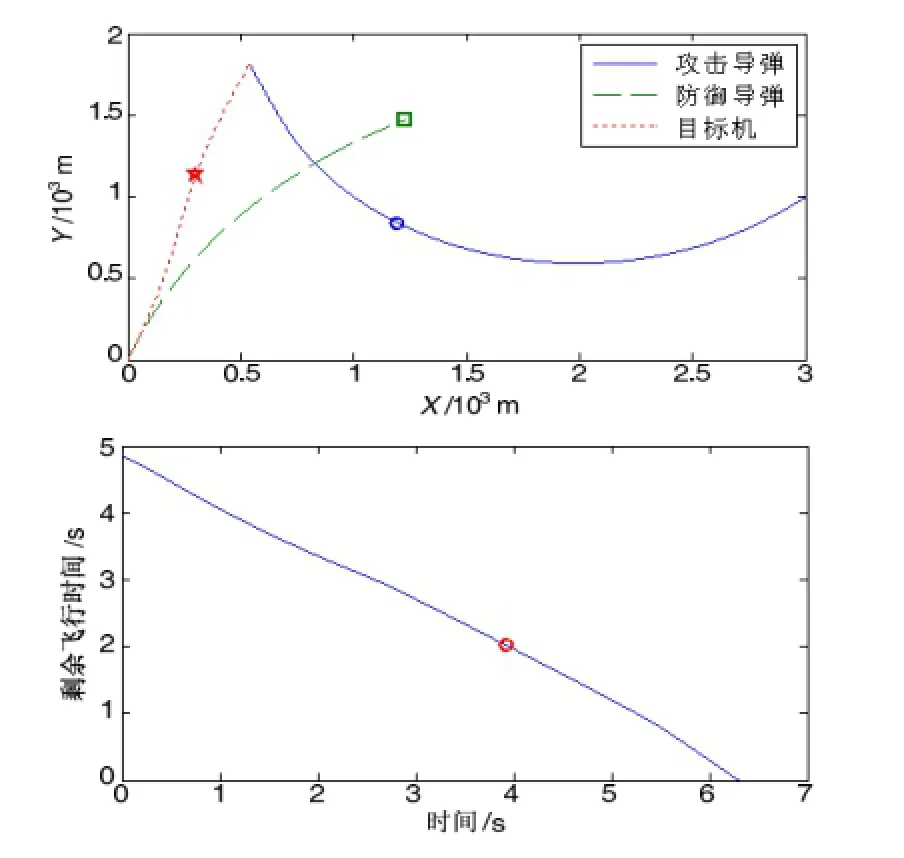
图2 飞行弹道与攻击导弹计算剩余飞行时间， m 18u g=Fig.2 Flight trajectory and the calculated time-to-go of attacking missile,m 18u g=

图3 飞行弹道与攻击导弹计算剩余飞行时间，m 25u g=Fig.3 Flight trajectory and the calculated time-to-go of attacking missile,m 25u g=

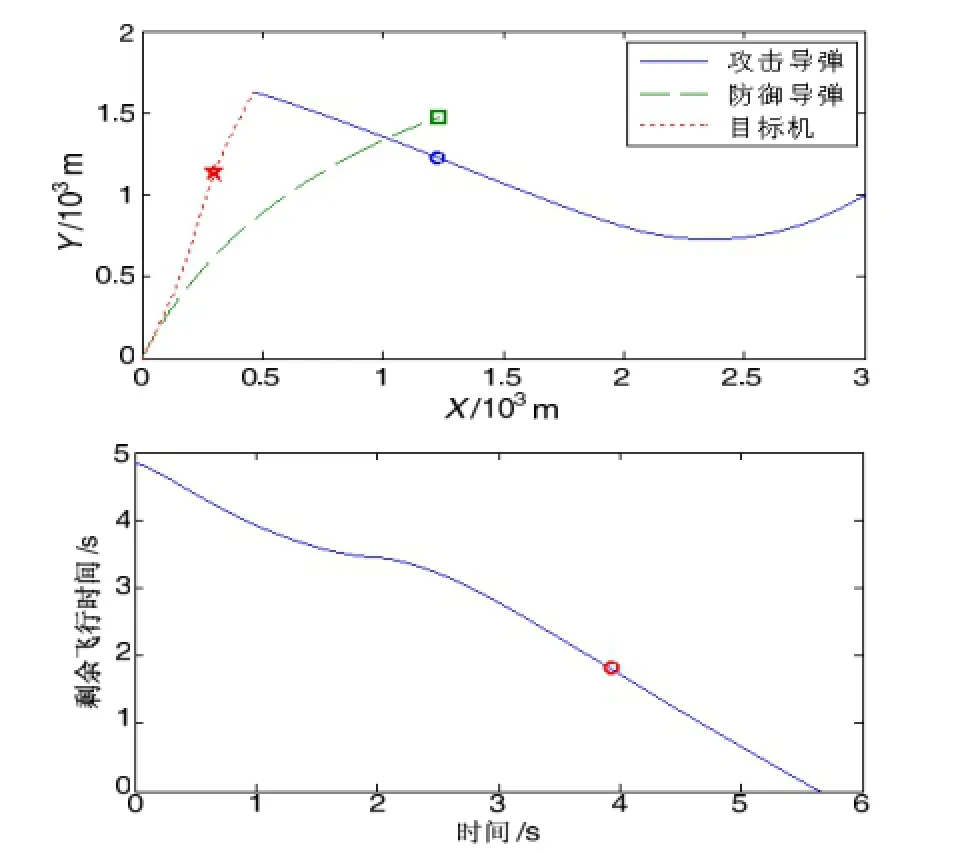
图4 飞行弹道与攻击导弹计算剩余飞行时间，m 30u g=Fig.4 Flight trajectory and the calculated time-to-go of attacking missile,m 30u g=

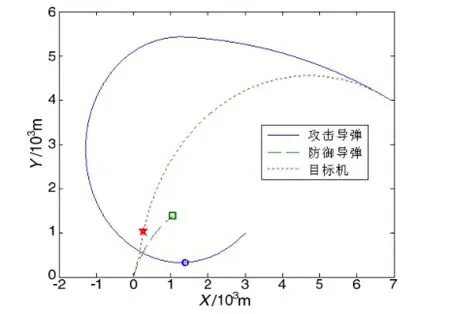
图5 飞行弹道， m 10u g=Fig.5 Flight trajectory,m 10u g=

4 结 论

针对攻击导弹在拦截目标飞机的同时还规避防御导弹的情形进行了研究。基于微分对策理论且考虑有界控制的情形，推导了攻击导弹的微分对策制导律、目标的逃逸策略和防御导弹的拦截策略。非线性系统仿真表明，攻击导弹在摆脱防御导弹的同时可实现对目标的有效拦截。该制导律要求同时获取目标飞机和防御导弹的信息，适用于末制导攻击情形，且要求导引头具有多目标跟踪能力。

（References）：

[1] Perelman A, Shima T, Rusnak I. Cooperative differential games strategies for active aircraft protection from a homing missile[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 761-773.

[2] Shaferman V, Shima T. Cooperative multiple model adaptive guidance for an aircraft defending missile[J]. Journal of Guidance, Control and Dynamics, 2010, 33(6): 1801-1813.

[3] Ratnoo A, Shima T. Line-of-sight interceptor guidance for defending an aircraft[J]. Journal of Guidance, Control and Dynamics, 2011, 34(2): 522-532.

[4] Ratnoo A, Shima T. Guidance strategies against defended aerial targets[J]. Journal of Guidance, Control and Dynamics, 2012, 35(4): 1059-1068.

[5] Rubinsky S, Gutman S. Three body guaranteed pursuit and evasion[C]//AIAA Guidance, Navigation, and Control Conference. Minneapolis, Minnesota, USA, 2012: 1-24.

[6] 花文华, 陈兴林, 宋申民. 主动防御的协同微分对策制导[J]. 高技术通讯, 2012, 22(1): 94-99.

Hua Wen-hua, Chen Xing-lin, Song Shen-min. Cooperative differential game guidance strategy for active defense [J]. Chinese High Technology Letters, 2012, 22(1): 94-99.

[7] Rusnak I. Advanced guidance laws for acceleration constrained missile, randomly maneuvering target and noisy measurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 456-464.

[8] Hexner G, Shima T. Stochastic optimal control guidance law with bounded acceleration[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 71-78.

[

9] Hexner G, Shima T, Weiss H. LQG guidance law with bounded acceleration command[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 77-86.

[10] Shinar J, Shima T. Nonorthodox guidance law development approach for intercepting maneuvering targets[J]. Journal of Guidance, Control and Dynamics, 2002, 25(4): 658-666.

[11] 花文华, 孟庆龄, 张拥军. 寻的导弹范数型微分对策制导律[J]. 高技术通讯, 2013, 23(4): 392-399.

Hua Wen-hua, Meng Qing-ling, Zhang Yong-jun. Norm differential game guidance laws for homing missiles. Chinese High Technology Letters, 2013, 23(4): 392-399.

[12] Rusnak I, Lev M. Optimal guidance for high-order and acceleration constrained missile [J]. Journal of Guidance and Control, and Dynamics, 1991, 14(3): 589-596.

[13] Shinar J, Turetsky V, Oshman Y. Integrated estimation/ guidance design approach for improved homing against randomly maneuvering targets[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(1): 154-161.

[14] Shaferman V, Shima T. Cooperative multiple model adaptive guidance for an aircraft defending missile[J]. Journal of Guidance, Control and Dynamics, 2010, 33(6): 1801-1813.

Guidance law of bounded-control missile for attacking an aircraft with defending missile

HUA Wen-hua1, MENG Qing-ling1, ZHANG Jin-peng1,2, ZHANG Yong-jun1
(1. China Airborne Missile Academy, Luoyang 471009, China; 2. Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons, China)

To improve the kill probability of attacking missile for target aircraft interception while avoiding a defending missile, a guidance law for attacking missile is presented based on differential game theory. The differential game theory has natural advantages for game of multi-body with independent control. As compared to optimal guidance law, the differential game guidance law further takes into account of the bounded control of attacking missile and is adapted to the attacking missile, target aircraft and defending missile with high-order control dynamics. Nonlinear simulations are carried out to verify performance of the guidance law, and the results show that the attacking missile can intercept the target with near zero miss distance while avoiding the defending missile successfully. To fulfill the avoiding and intercepting mission, the attacking missile only needs two times maneuvering performance against the defending missile.

guidance law; differential game guidance; bounded-control missile; target interception

V448.133

A

1005-6734(2016)01-0103-05

10.13695/j.cnki.12-1222/o3.2016.01.019

2015-09-05；

2015-11-29

航空科学基金资助项目（2015ZC12006）

花文华（1983—），男，高级工程师，博士，主要研究方向为飞行器制导与控制。E-mail: huawh6611@163.com