GNSS网络实时动态模糊度解算病态性解决策略
邓 健,王胜利,陈润静
(1.厦门理工学院 计算机与信息工程学院,厦门 361024;2.山东科技大学 海洋工程研究院,青岛 266590)
GNSS网络实时动态模糊度解算病态性解决策略
邓 健1,王胜利2,陈润静1
(1.厦门理工学院 计算机与信息工程学院,厦门 361024;2.山东科技大学 海洋工程研究院,青岛 266590)
针对 GNSS网络实时动态(RTK)参考站间模糊度解算病态性问题,分析了病态性对模糊度浮点解影响,并基于无电离层组合解算模糊度基本模型,提出了改善模型病态性的两种策略。①参数选取策略:针对高仰角卫星,采用相对天顶对流层参数代替常规双天顶对流层参数设置,减少待估参数以改善病态性;②参数相关性优化策略:将GNSS卫星模糊度解算分为较易固定和较难固定两类,首先获取较易固定模糊度整数解,并反演天顶对流层延迟信息,再将该信息作为先验信息对较难固定模糊度解算模型进行约束,通过减小天顶对流层与模糊度相关性改善病态性。算例分析表明:两种策略在初始历元法方程病态性就明显优于常规模型,且只要通过少数十几个甚至几个历元就能够快速减弱法方程的病态性。该方法不需要考虑附加矩阵或参数的设置,易于实际工程应用。
病态性;模糊度解算;网络实时动态;无电离层组合
病态性问题是GNSS载波模型难以实现高精度快速定位的主要影响因素。引起观测方程出现病态主要由以下两方面因素[1]:第一类是由于参数间存在近似线性关系,如位置参数、对流层延迟参数与整周未知数的关系等;第二类是由于观测所提供的信息量不足以确定待定参数,如北斗系统中高轨卫星,卫星运行速度慢,卫星结构变化缓慢,观测值所提供的信息量显著地少于解算待定参数的要求。针对卫星导航定位模型病态性,早期Teunissen教授使用条件数法分析了GPS系统中双差模型法方程协方差阵模糊度分量的病态性,说明协方差阵的条件数变化缓慢[2-3],该项研究为模糊度解算降相关提供了理论依据。在改善载波双差定位模型病态性方面,代表性的方法主要分为两大类:第一类为正则化法。该方法关键在于构造正则化矩阵与参数。不少研究人员在分析GPS快速定位法方程特征的基础上,提出了相应的正则化矩阵构造方法[4-7]。文献[8-9]通过引入选权拟合构造正则化矩阵对参考站坐标进行约束,改善法矩阵病态性。第二类为岭估计方法。该类方法是从减小均方差的角度出发而提出的一种有偏估计方法,如,约束三个坐标参数的部分岭估计方法[10]、约束坐标参数和模糊度参数的双k岭估计方法[11]。文献[12]将部分岭估计法应用于北斗GEO/IGSO高轨卫星,改善了模型的病态性,提高了定位的精度和效率。
上述两类方法主要是通过修正法方程系数阵,改善快速定位中模型的病态性,其有效性主要在于正则化矩阵R及岭参数k的选取。本文将针对GNSS网络RTK参考站间模糊度解算中无电离层组合观测模型,从待估参数选取和参数相关性优化策略上,改善模型的病态性。
1 网络RTK无电离层组合模糊度解算模型
在网络RTK中较常用的模糊度解算方法是先固定双差宽巷模糊度,然后构造无电离层组合实现基础载波模糊度解算。考虑到参考站通常建设在较空旷的地方,卫星位置可采用精密星历计算,因此暂不考虑多路径效应及轨道误差影响。无电离层组合基本方程为[13]

式中:∇Δ表示卫星间、接收机间的双差算子,IFφ∇Δ为无电离层组合观测量, ρ∇Δ 为双差卫地距, T∇Δ 为双差对流层延迟,1f、2f为载波频率,Wλ、Nλ为宽巷及窄巷组合观测量的波长,WN∇Δ 为宽巷组合模糊度,1N∇Δ 为1f载波双差模糊度。对于宽巷组合模糊度顾及长波长特性,通过 Melbourne-Wubbena组合等方法可获得成功率较高的固定解,这里不再详细论述。因此,可以确定式的主要影响源来自对流层的双差残余,一般将其表示为天顶延迟Ztd与关于卫星高度角E的映射函数MF(E)的乘积。对于基线AB和卫星对i、j间形成的双差对流层延迟可以表示为
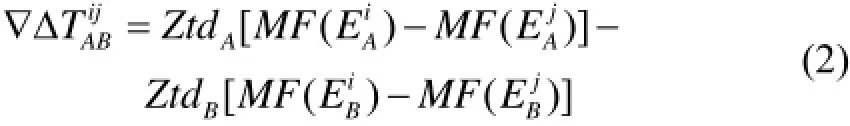
将式(2)带入式(1),在宽巷整周模糊度固定基础上,有如下观测方程:

式中:∇为星间单差算子,对应如下误差方程:

其中,
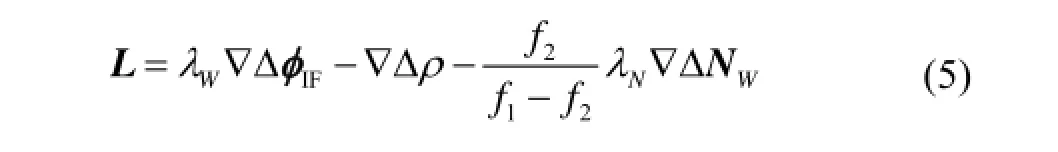
简化为

其最小二乘解:


2 病态性对模糊度浮点解影响分析
在模糊度解算过程中,通常是利用已求解的模糊度浮点解及其方差快速估计整周模糊度,因此,式(8)中模糊度浮点解 ˆX的正确性是整周模糊度估计的前提和基础。例如,在采用LAMBDA算法估计整周模糊度时,当浮点解精度较低或出现较大偏差时,无论采用何种方法去相关搜索变换,都很难提高整周模糊度的搜索效率,甚至产生错误的估计值。
在法方程中,假定N、W中有微小的扰动δN、δW ,相应的参数估值 ˆX有偏差值 ˆδX,则扰动后的法方程可表示成:

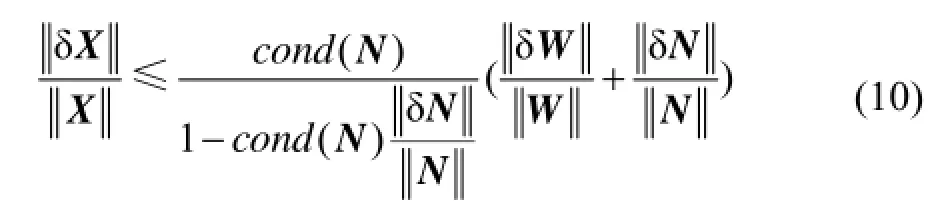

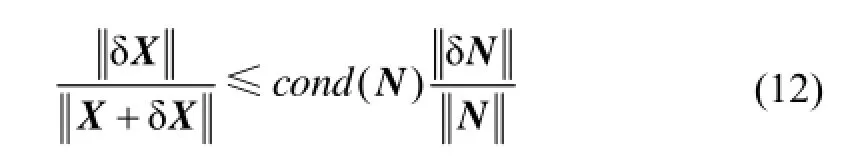
从式(10)~(12)可知,条件数较大时,若N及W有较小的扰动δN、δW,就会引起参数解的较大波动,此时模糊度浮点解与准确值将产生较大偏差。图1选取了两参考站模糊度解算中两颗卫星浮点解随法方程条件数的变化情况,其中PRN10为低仰角卫星(仰角变化范围为17º~21º),PRN17为高仰角卫星(仰角变化范围为63º~59º)。由图1可以看出,在前50个历元中,法方程条件数非常大,达到109,从而引起卫星PRN10、PRN17双差模糊度浮点解与准确值产生较大波动,特别是对于低仰角卫星PRN10,由于观测噪声大,经法方程条件数成倍放大后,模糊度浮点解受其扰动出现了数周的偏差。随着观测历元增多,观测值所提供信息量逐渐增大,法方程条件数减小,法方程由病态方程逐渐转换为良态方程,双差模糊度浮点解波动较小。因此可以看出,方程病态性直接影响模糊度浮点解解算的准确性和可靠性。

图1 病态条件下法方程条件数及浮点解Fig.1 Condition number of normal equation and float resolution of ambiguity under ill-conditioned
3 模型病态性解决策略
对于上述无电离层组合模型,一方面由于观测历元数不足以确定待定参数引起法方程病态,另一方面则主要是由于参数间的相关性,即两个天顶对流层参数之间的相关性以及对流层参数与模糊度参数之间的相关性[14]。为此,以下将从对流层参数选取及参数相关性优化策略改善模型病态性。
3.1 基于相对天顶对流层延迟的病态性解决策略
模糊度解算过程中在一定时间内所有观测历元未知数个数是一定的。对于前几个历元,虽然观测值个数远多于未知数个数,但是由于相邻两组观测卫星的空间位置关系变化甚小,观测值所提供的信息量显著地少于解算待定参数的要求,从而导致系统病态。因此,若能够尽可能地减少不必要待估参数个数,则在相同观测条件情况下,需要观测信息减少,必将间接减小模型病态性。对于无电离层组合式(3)中分别设置了对流层天顶延迟参数AZtd、BZtd,假设能用两参考站相对天顶对流层延迟作为参数代替,则减少了待估参数个数,这有利于改善模型病态性。参考式(2),上述假设前提是当两参考站星间单差映射函数近似相等,即研究表明[15],当卫星仰角大于 30°时,两参考站星间单差映射函数近似相等所产生的对流层估计误差小,不影响模糊度解算。因此,对高仰角卫星,将对流层延迟表示为参考站相对天顶对流层与MF映射函数的乘积:(13)


为了测试上述方法的有效性,本文选取了苏州CORS中,基线长为64 km的两个站点10 min GNSS观测数据,采样率1 s,分别采用常规双天顶对流层参数设置(式4)及相对天顶对流层参数(式14)两个模型,其中常规模型中又根据卫星截止高度角的不同分为两个测试方案,三种方案的基本参数设置如表1所示。

表1 三种方案基本参数Tab.1 Parameters of three kinds of test scheme
在三种方案中,分别采用单个系统(以 BDS为例)以及组合系统(GPS/GLONASS双系统、GPS/GLONASS/ BDS三系统)的观测数据比较分析对应的法方程条件数,图2为各系统卫星分布情况。
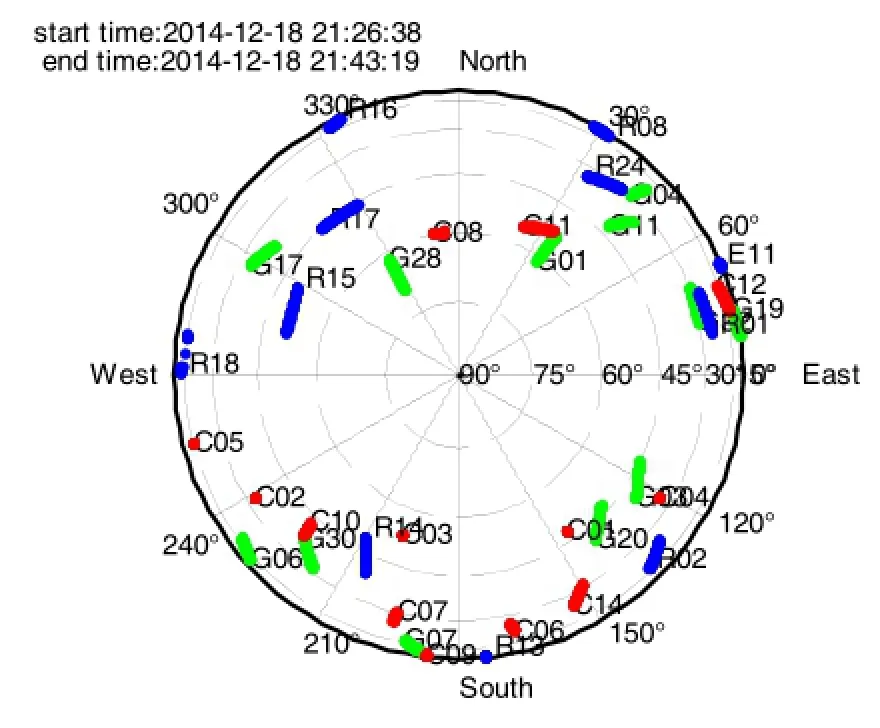
图2 卫星分布图Fig.2 Distribution map of satellites
从图3不同系统组合下三种方案法方程条件数变化情况可以看出,不管是单个系统还是组合系统,在前几个历元中,采用相对天顶对流层模型(方案3)法方程条件数优于双天顶对流层模型(方案1、方案2)1~2个数量级。在收敛性方面,方案3只要经过少数十几个历元即可快速收敛,而方案1和方案2通常需要几十个甚至上百个历元才能有效收敛,直接影响模糊度固定的效率,因此,采用相对天顶对流层参数设置策略可以很好改善模型的病态性。另一方面,对比方案1和方案2,其主要差别在于卫星数量,由于方案1中卫星数量较多,未知数个数也相对较多,因此,前几个历元中条件数较方案2大,但由于观测过程中待估参数个数一定,随着历元数的增多,方案1中观测信息量急剧增多,特别对于组合系统,对应条件数收敛速度明显优于方案 2。此外,从单系统和组合系统分析,无论哪种方案,三系统GPS/GLONASS/BDS病态性优于双系统GPS/GLONASS,单系统BDS方程病态性最为严重。

图3 不同系统组合下三种方案法方程条件数变化情况Fig.3 Changes of the condition number with three test schemes in different systems
3.2 基于对流层约束的病态性解决策略
在GNSS模糊度解算中,通常会存在一些卫星模糊度较容易固定,如,受观测噪声影响小的高仰角卫星,以及多系统模糊度固定中具有三个或多个频率观测信息的卫星,那么我们可以先固定这类卫星模糊度,在此基础上,反演对流层延迟信息,并将其作为先验信息约束剩余卫星模糊度解算模型,降低天顶对流层参数与模糊度参数之间的相关性,减弱模型病态性。
综上分析,可将卫星的模糊度分为两类,一类是较容易固定的模糊度eN∇Δ ,另一类为较难固定。则误差方程式(4)可以变换为


在上述解算过程中,较容易固定的卫星并未起到其优势,如果将较容易固定的卫星首先固定,然后将其带入误差方程,则公式(15)即可变换为

其估值为

选取苏州CORS中基线长度分别为40 km、66 km以及94 km的三条基线,概略位置如图4所示。任意选择采样率为1 s 的10 min GNSS观测数据,对比分析采用一般解算模型(式16)及对流层约束模型(式18)下法方程条件数变化情况。

图4 站点分布概略图Fig.4 Distribution map of stations
对于对流层约束模型,考虑到在GPS、GLONASS及BDS系统中,BDS是现有的唯一全系统播发三频信号的卫星导航系统。三个频率有利于构成多种特性较优的组合观测量,以快速固定模糊度。众多学者对此进行了相关研究,提出了一些有效的解算方法[16-18],这里不再详细论述。为此,算例中将北斗模糊度归为较容易固定的一类,可通过三频组合预先固定模糊度,而后反演对流层延迟信息,并将其作为先验信息约束 GPS/GLONASS模糊度解算模型,以减弱法方程病态性。图5分别给出了三条基线在两种模型下法方程条件数的变化情况,很明显,在不同长度基线下,具有对流层约束模型的法方程条件数从初始历元开始就比常规解算模型小几个数量级,方程的病态性得到很好的改善,从而有利于模糊度浮点解的求解。


图5 三条基线两种模型法方程条件数变化情况Fig.5 Condition number vs. epoch for two resolution models
4 结 论
法方程病态影响模糊度浮点解的准确性和可靠性,不同于正则化和岭估计方法。本文主要基于模糊度解算的无电离层模型,提出从对流层参数选取及参数相关性优化策略上改善模型病态性,通过理论推导及算例验证表明,该两种策略在初始历元模型法方程病态性就明显优于常规模型,且只要通过少数十几个甚至几个历元,就能够快速改善法方程的病态性,从而有利于模糊度浮点解的快速可靠解算。此外,该策略不需要考虑附加矩阵或参数的设置,易于实际工程应用。
(References):
[1] 卢秀山, 冯遵德, 刘纪敏. 病态系统分析理论及其在测量中的应用[M]. 北京: 测绘出版社, 2007, 7-15.
[2] Teunissen P J G. A new method for fast carrier phase ambiguity estimation[C]//IEEE Position Location and Navigation Symposium, 1994: 562-573.
[3] Teunissen P J G. The invertible GPS ambiguity transformations[J]. Manuscripta geodaetica, 1995, 20(6): 489-497.
[4] Ou J, Wang Z. An improved regularization method to resolve integer ambiguity in rapid positioning using single frequency GPS receivers[J]. Chinese science bulletin, 2004, 49(2): 196-200.
[5] Cai J, Grafarend E W, Hu C, et al. The uniform Tykhonov-Phillips regularization (α-weighted S-homBLE) and its application in GPS rapid static positioning[C]//VI Hotine-Marussi Symposium on Theoretical and Computational Geodesy. Springer Berlin Heidelberg, 2008: 216-224.
[6] Cai J, Hu C, Grafarend E W. The optimal regularization method and its application in GNSS rapid static positioning[J]. ION GNSS Proceedings, Fort Worth, 2007: 299-305.
[7] Li B, Shen Y, Feng Y. Fast GNSS ambiguity resolution as an ill-posed problem[J]. Journal of Geodesy, 2010, 84(11): 683-698.
[8] 罗孝文, 欧吉坤. 中长基线 GPS 网络 RTK 模糊度快速解算的一种新方法[J]. 武汉大学学报(信息科学版), 2007(2): 156-159. Luo Xiao-wen, Ou Ji-kun. A new approach for fast integer ambiguity resolution suitable for medium-long baseline in GPS network RTK[J]. Geomatics and Information Science of Wuhan University, 2007(2): 156-159.
[9] Luo X, Ou J, Yuan Y, et al. An improved regularization method for estimating near real-time systematic errors suitable for medium-long GPS baseline solutions[J]. Earth Planets and Space (EPS), 2008, 60(8): 793.
[10] 归庆明, 郭建锋. 部分岭估计在整周模糊度解算中的应用[J]. 信息工程大学学报, 2004, 5(2): 137-139. Gui Qing-ming, Guo Jian-feng. A new ambiguity resolution based on partial ridge estimator[J]. Journal of Information Engineering University, 2004, 5(2): 137-139.
[11] 归庆明, 韩松辉, 吴炳荣, 等. 双 k 型岭估计及其在GPS 快速定位中的应用[J]. 测绘科学技术学报, 2006, 23(1): 8-10. Gui Qing-ming, Han Song-hui,Wu Bing-rong, et al. Double k type ridge estimation and its applications in GPS rapid positioning[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(1): 8-10.
[12] 王胜利, 王庆, 聂文峰, 等. 北斗系统高轨卫星高精度定位模型病态性分析及改进方法[J].导航定位学报, 2013, 1(3): 31-35. Wang Sheng-li, Wang Qing, Nie Wen-feng, et al. Analysis and solution of ill-conditioned problems in BeiDou system high-precision high-orbit satellite positioning model[J]. Journal of Navigation and Positioning, 2013, 1(3): 31-35.
[13] 黄丁发, 熊永良, 袁林果. 全球定位系统(GPS)——理论与实践[M]. 成都: 西南交通大学出版社, 2006: 205-209.
[14] 王胜利, 王庆, 杨徉, 等. 北斗 IGSO/GEO/MEO卫星联合高精度定位方法[J].中国惯性技术学报, 2013, 21(6): 792-796. Wang Sheng-li, Wang Qing, Yang Yang, et al. Method of high-precision joint positioning of satellite IGSO/GEO/ MEO[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 792-796.
[15] Deng J, Wang S L. Divisional ambiguity resolution for long-range reference stations in network RTK[J]. Survey review, 2015, 47(343): 272-278.
[16] Wang K, Rothacher M. Ambiguity resolution for triplefrequency geometry-free and ionosphere-free combination tested with real data[J]. Journal of Geodesy, 2013, 87: 539-553.
[17] Tang W, Deng C, Shi C, et al. Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system[J]. GPS Solutions, 2013: 1-10.
[18] Montenbruck O, Steigenberger P, Teunissen P, et al. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system[J]. GPS Solution, 2013, 17: 211-222.
Resolving strategies for ill-posed equation in ambiguity resolution of GNSS network real-time kinematics
DENG Jian1, WANG Sheng-li2, CHEN Run-jing2
(1. School of Computer and Information Engineering, Xiamen University of Technology, Xiamen 361024, China; 2. Institute of Ocean Engineering, Shandong University of Science and Technology, Qingdao 266590, China)
The ill-posed problem in ambiguity resolution between reference stations in network RTK(real-time kinematic) has adverse influence on the float solution of the ambiguity. Based on the analysis on this influence and by using an ionosphere-free linear combination model, two strategies are put forward: One is the parameter-selecting strategy, which improves the ill-posed equation for satellites at high elevation by reducing the unknown parameters, that is, a single relative zenith tropospheric parameter was applied instead of conventional two zenith tropospheric parameters. The other is by optimizing the parameter’s correlation, in which the ambiguities to be resolved are classified into two categories, one is easy to be fixed, and the other is difficult to be fixed. The former parameters are estimated and then inversely calculated to obtain the zenith tropospheric delay parameters, and then they are used as priori information to constrain the model. Thus the correlation between the zenith tropospheric parameters and the ambiguities is weakened, which improves the ill-posed equations. Test results for the two strategies show that the normal equations formed at initial epochs are evidently less ill-posed, compared with the conventional models. The ill-posed state of the normal equation can be rapidly weakened only by a few dozen or even several epochs. This method doesn’t need to set the additional matrix or parameters, and can be easily applied into practical application.
ill-posed; ambiguity resolution; network RTK; ionosphere-free linear combination
P228.1
A
1005-6734(2016)01-0014-06
10.13695/j.cnki.12-1222/o3.2016.01.004
2015-10-14;
2016-01-20
国家自然科学基金(41204032);福建省自然科学基金(2015J01176)
邓健(1981—),男,副教授,从事卫星导航定位技术与应用研究。E-mail: dengjian163@126.com
——环地平弧&环天顶弧

