油井管上扣过程中摩擦磨损对摩擦因数影响分析
曹 杉,高进伟,孔祥领,党 民,闫柏辰
(中国石油技术开发公司,北京 100028)①
油井管上扣过程中摩擦磨损对摩擦因数影响分析
曹杉,高进伟,孔祥领,党民,闫柏辰
(中国石油技术开发公司,北京 100028)①
摘要:特殊螺纹油井管和传统的API油井管在现场使用中都应按推荐上扣转矩进行操作,而转矩值的计算与两接触表面间的摩擦因数密切相关。目前,摩擦因数由经验数据给出,且在API标准中通常设置为常数,忽略了表面性能和操作环境等方面的影响,使上扣转矩的计算不准确;尤其在高温、高压等复杂井况中,可能引起螺纹泄露或过扭涨扣等。建立了相应理论模型,仿真了上扣过程中螺纹表面的摩擦磨损对摩擦因数的影响;分析了随着滑移距离的增大,表面形貌、粗糙度及摩擦因数的变化趋势。仿真结论表明,由于上扣过程中的“磨损抛光效应”,摩擦因数逐渐降低,最终稳定在起始值的88%左右。这一研究对油井管上扣过程中的摩擦磨损、螺纹粘扣以及上扣转矩的确定具有一定的指导意义。
关键词:油井管;转矩;螺纹;摩擦因数
近年来,油气勘探开发难度逐渐增大,油井管服役条件日益苛刻[1-3],例如深井及超深井、高抗挤需求、高抗硫需求以及含有其他腐蚀气体等高难度井越来越多。在油井管的实际使用中,超过2/3的失效属于螺纹失效[4-5],而大多数螺纹失效都与粘扣相关,尤其是深海领域,螺纹粘扣引起了广泛的关注[6]。根据统计,2012年仅在北海地区,粘扣导致的产量下降、更换油井管柱等造成了数十亿美元的损失[7]。
1综述
为应对各种高难度井况,非API系列油井管的需求旺盛,对油井管螺纹接头的密封性能、连接强度以及抗腐蚀能力都有了更高的要求[8]。特殊螺纹设计的核心问题是通过优化和改进螺纹连接、密封面以及转矩台肩,最大程度地减少螺纹塑性变形、降低螺纹应力集中、确保接头密封[9],从而保证管柱的结构完整性和密封性能。Bradley等人[10]指出,为确保特殊螺纹在高温、高压环境下的应用,特殊螺纹连接的相关测试必须精确。考虑到成本原因,螺纹设计与测试中使用最多的仍然是有限元分析方法[4,11-12]。
根据API RP 5C5(ISO 13679)的定义[13],油井管螺纹粘扣是发生在相互接触的金属表面之间的冷焊,是螺纹表面的连续性、完整性和尺寸精度遭到破坏的一种失效现象[14]。粘扣主要是在高接触压力、高温和/或高速加载的作用下,金属表面发生弹性变形、塑性变形、挤压剥落、犁沟和嵌入金属的损伤过程[15]。在决定螺纹是否会发生粘扣的影响因素中,油井管的上扣转矩是最为重要的参数之一,尤其对于复杂工况,合理的转矩值尤为重要[10]。一方面,上扣转矩决定了管体与接箍之间能否形成有效密封,当转矩较小时,很可能形成泄露通道;另一方面,当转矩较大时,螺纹之间、金属-金属密封之间容易产生塑性变形,从而导致粘扣。
为了有效防止上述弊端,应当合理计算转矩的推荐值。以钻具为例,上扣转矩值根据Duggan的转矩方程计算[16],该方程是基于螺栓、螺母间的滑移模型推导的。上扣转矩与摩擦因数之间的关系[17]为
(1)
式中:Ym为材料的最小屈服强度;p为螺纹导程;θ为螺纹角度;Rt、Rs为与螺纹尺寸相关的参数;A是与应力释放槽相关的几何参数;f为摩擦因数,根据API RP 7G,对于紧密配合的螺纹或台肩表面,使用质量分数40%~60%金属锌的螺纹脂时,摩擦因数约为0.08[17]。
由此可见,螺纹表面的摩擦因数对推荐转矩值的计算有显著影响。API RP 5A3的推荐做法中给出了估算摩擦因数的基本方法,测试系统则由马达、转矩传感器和旋转角度传感器等组成,测试样品为螺栓、螺母,如图1所示[18]。其中,马达提供了螺栓的旋转并输出转矩,分别由2种传感器读出各状态下的转矩值和旋转角度,从而计算对应的摩擦因数。根据API RP 5A3中的描述,油套管螺纹连接的接触压力为35~140 MPa;若螺纹脂分布较薄,表面接触压力可高达200~425 MPa[18];而在特殊螺纹中可达690 MPa[19-20],远高于API RP 5A3的测试状态。因此,在同等润滑条件下,当承载增大时,润滑条件恶化、粘扣风险增加,API测试中得到的摩擦因数低于现场的实际情况。
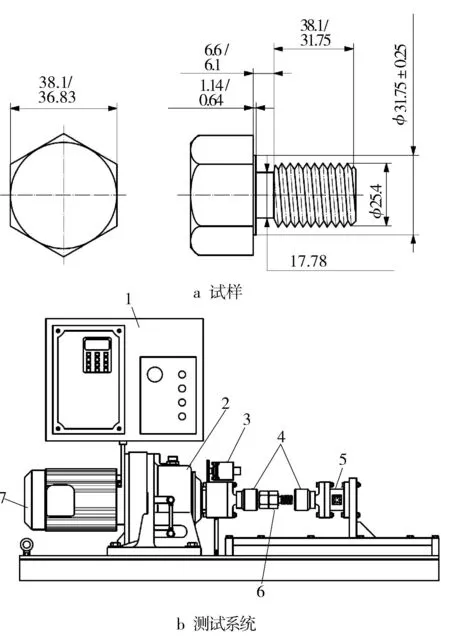
1—控制面板;2—齿轮箱;3—旋转传感器;4—内六角固定头;
摩擦因数不但取决于上述接触压力的大小,还与接触表面的基本性能以及动态性能[21]相关。螺纹在实际拧接中的摩擦磨损也会对摩擦因数产生影响,称为“磨损抛光效应”。所谓磨损,即接触表面之间由于相对运动造成一定材料损失的现象[22],通常用单位时间、单位滑行距离下的表面磨损量来衡量磨损的速率[23]。由于磨损的复杂性,目前尚未有统一的理论解释,因为环境中每一个微小变量都会导致整个摩擦磨损体系的变化。Coulomb[24]指出了表面粗糙度对摩擦因数的影响;Nayak[25]对高斯分布各向异性的随机表面进行研究,抽象出表面的数学描述模型;Bengisu等人[21]表达了宏观摩擦力与表面微观尺度之间的关系,研究出一套考虑了变形和表面微凸体粘结的模型,并指出宏观摩擦力与微观力之间的关系与微观形貌下“实际接触”的表面相关;Sedlacek等人[26]发现在干摩擦的情况下,表面粗糙度越低,相对的摩擦因数也越低,而在湿摩擦的情况下,随着表面粗糙度的降低,摩擦因数先降低后增加,表明了不同的摩擦磨损机理;Meng等人[27]指出,控制表面粗糙度有助于实现更好的金属-金属密封,同时,当表面的接触面积增大时,接触压力降低,从而产生更均匀的膜厚;Shafiei和Alpas[28]则通过试验表明,滑移速度增大时摩擦因数也随之增大;Farhat等人[29]则研究了纳米晶体铝材料中晶粒度与摩擦因数的关系,指出随着晶粒度降低,摩擦因数也随之降低,并且随着滑移距离的增大,磨损量在一定滑移距离后维持在相对稳定的水平。
在有润滑油的情况下,根据Stribeck曲线,可定义4类润滑模式:边界润滑(或称薄膜润滑)、混合润滑、弹性流体润滑及流体动压润滑[30],如图 2所示。从中可见不同润滑模式下摩擦因数的变化趋势。
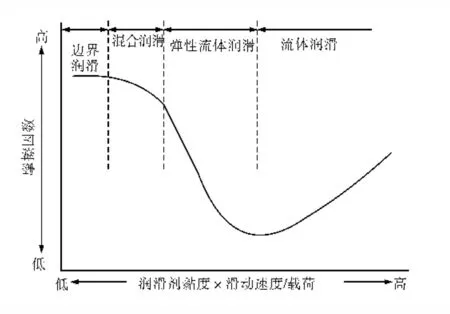
图2 Stribeck曲线中润滑状态与摩擦因数的关系
为保证油井管在实际工况与现场使用的性能,上扣转矩是非常重要的参数,而上扣转矩的计算取决于摩擦因数的值。根据API标准和推荐做法,通常将摩擦因数视为常数。但实际上不同的润滑状态、接触压力、滑移速度(即上扣速度)、滑移距离(即上扣次数)和螺纹表面粗糙度都会对摩擦副产生影响;不同表面在不同状态下的摩擦因数是不一致的。目前,摩擦因数值计算的上扣转矩也不尽准确,很可能导致实际拧接中的过扭或拧接不足;对一般的石油管柱而言,上扣转矩的微量偏差不会产生较大的影响,但对于一些高温、高压井,上扣转矩不准确则会出现更大的风险,甚至发生灾难性事故。因此,应更加深入的研究影响摩擦因数的因素,包括材料及表面性能、螺纹脂性能、接触压力、滑移速度、滑移距离以及其他相关参数的影响。本文通过MATLAB建模与仿真,计算在油气田现场使用中油井管的摩擦因数,从而更准确地计算上扣转矩,指导特殊螺纹连接的设计,确保油井管在现场的安全使用。
2上扣过程中磨损抛光效应模型
通过建立上扣过程中的磨损抛光效应模型,分析在摩擦磨损中表面粗糙度以及磨损量的变化。在Archard磨损理论的基础上,引入了考虑微观形貌的Christensen模型,通过MATLAB仿真分析了微观形貌对润滑性能的影响,即“磨损抛光效应”使接触表面的粗糙度降低,从而影响了系统的润滑性能。
2.1基于Archard理论的磨损模型
磨损模型由Archard于1953年提出[31],Archard采用摩擦表面微凸体粘着结点为半球状的简化模型,认为当两个接触表面之间存在相对运动时产生磨损,取决于载荷和材料特点等因素,即
(2)
式中:V是磨损量;s是滑移距离;k是磨损因数的无量纲参数;FN是微凸体承受的正载荷;H是较软材料的布氏硬度。
由式(2)可知,磨损量与正载荷成正比,与布氏硬度成反比。正压力越大,接触压强越大,材料磨损量越大。对式( 2 )两边时间求导可得:
(3)
式中:p为载荷压强;v为滑移速度;dh/dt为单位时间内的磨损深度,即磨损速率。
由式(3)可知,载荷压强和滑移速度越大、硬度越小时,磨损速率越大。
考虑到螺纹脂的存在,上扣过程在微观层面实际是表面微凸体和微凹坑中的润滑油之间的作用,因此体现出与宏观作用不一致的特点。根据Le等人[32]文献,接触中的实际压强满足:
(4)
式中:pa是微凸体间的接触压力;pv是微凹坑中润滑油的油压;Aa是微凸体所占的面积百分比,则1-Aa为微凹坑所占面积百分比。
当两个粗糙表面接触时,其接触部分具有不连续性和不均匀性[33],“实际”接触面积只是“名义”接触面积中的一部分[34]。接触压强等于接触压力除以接触面积,实际情况中的接触压力远大于按名义接触面积计算的接触压力。为抽象、简化接触表面的微观形貌,Christensen[35]引入了基于随机函数的粗糙表面数学模型。本文基于该模型,仿真了磨损过程中实际接触压力的变化。
2.2微凸体的压扁与润滑油的泄露
根据Williams的推导[36],在弹性形变范围内平均压强为
(5)
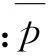
当引入润滑油时,基于Hamrock和Dowson的计算[37],润滑油的最小膜厚hmin为
(6)
式中:η是润滑油的黏度;u是两个相对滚动表面在Hertz接触区的平均速度,即为滑移速度的一半。
当正压力W提高时,油层厚度下降,从而导致微凸体间真实接触面积的提高。
润滑膜的厚度直接影响了润滑状态,但不能只考虑润滑膜的厚度,还必须考虑表面粗糙度的影响,只有润滑膜的厚度大于微凸体高度时,才能起到相应的润滑效果。为分析表面粗糙度对润滑特性的影响,定义膜厚比Λ为膜厚与摩擦副表面复合粗糙度的比值[22]。
(7)
式中:Rq,1与Rq,2分别为2个接触摩擦副的粗糙度。
通常认为,当Λ>3时,油层厚度大于表面平均粗糙度,因此2接触表面之间被油层隔离开,为流体润滑状态;当Λ<0.3时,由于油层厚度过低,两接触表面上的微凸体之间接触较多,边界润滑状态占主导。实际试验中测得的Λ分布于0.3~0.7[38]。为简化分析,本文认为带螺纹脂的上扣过程中以边界润滑状态为主。
根据Patir和Cheng[39]的通用流量模型,可模拟表面粗糙度对润滑性能的影响。定义qx为润滑油在单位长度上向接触单元外部的泄露流量。假设接触单元为半径为a的圆形,接触单元中的圆圈代表露出的微凸体区域,如图3所示。
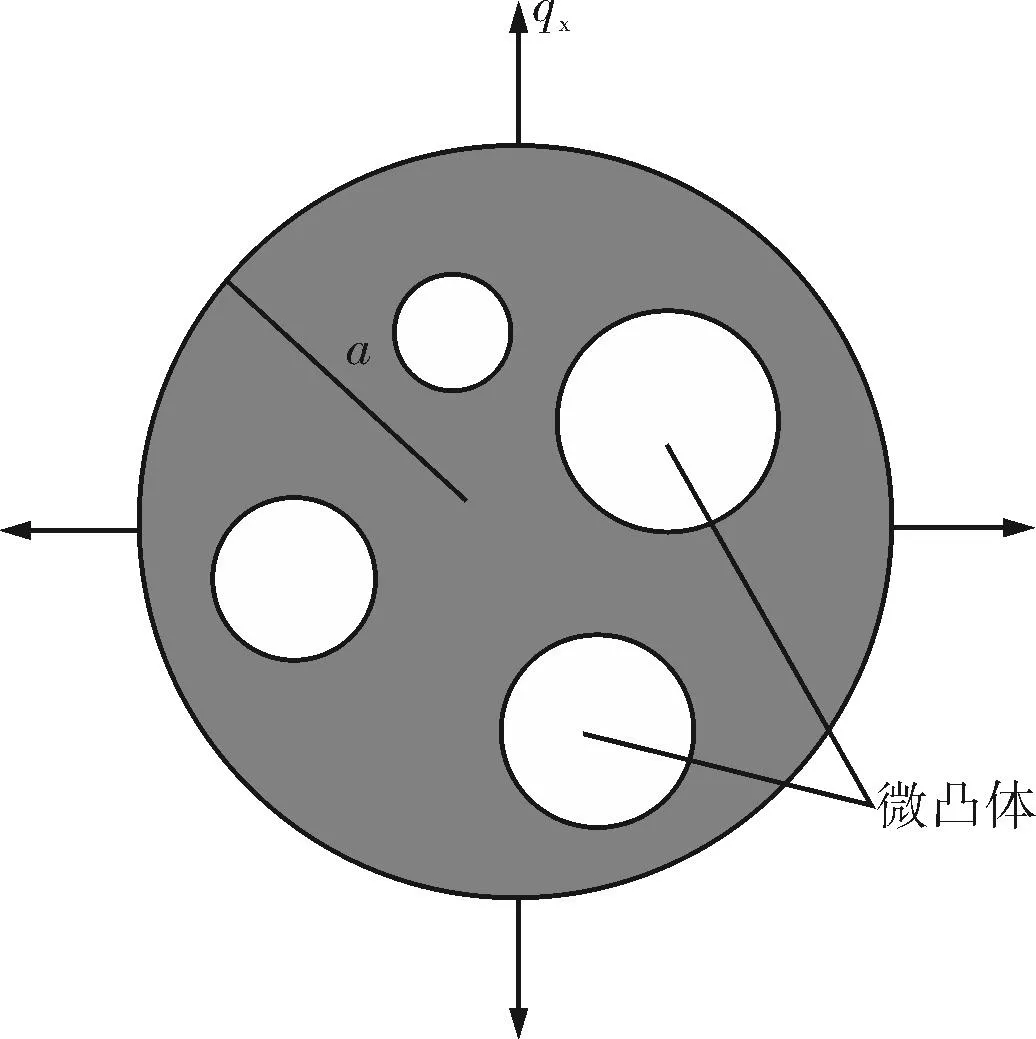
图3 接触单元示意
考虑到滑移速度较低,qx主要由压力梯度驱动,即:
(8)
式中:ht为平均油层厚度;Φx为流量因数,Φx的计算公式由Li[40]给出。
(9)
Htc=3[(1-(0.474 76/γ)+1)-0.250 07]
(10)
a2=0.051 375(ln(9γ))3-0.007 190 1(ln(9γ))4
(11)
a3=1.001 9-0.179 27ln(γ)+
(0.047 583ln(γ))2-(0.016 417ln(γ))3
(12)
式中:γ为表面粗糙度的Peklenik因数;Ht为平均油层厚度ht与表面粗糙度均方根的比值;Htc是泄露阈值,表示磨损后残留微凸体高度与原始表面微凸体高度间的比值。
为简化模型,可认为微凹坑中润滑油的流体静压力梯度dpv/dx=pv/a。则
(13)
假设表面粗糙度是各向同性的,因此,泄露流量是轴对称的,接触单元中润滑油体积的流出量满足式(14)。
(14)
接触单元中油层体积的减少量与磨损造成的微凸体高度的降低量有关。
由式(3)可得:
(15)
式(14)~(15)联立可得:
(16)
伴随着滑移距离的增大和磨损的加剧,微凹坑中的压力会逐步增大。联立式(4)、式(15)和式(16),在MATLAB仿真的连续条件下求解,可获得ht的变化量、微凸体接触面积比Aa、微凹坑油压pv和微凸体接触压力pa与滑行距离的关系曲线,如图4所示。
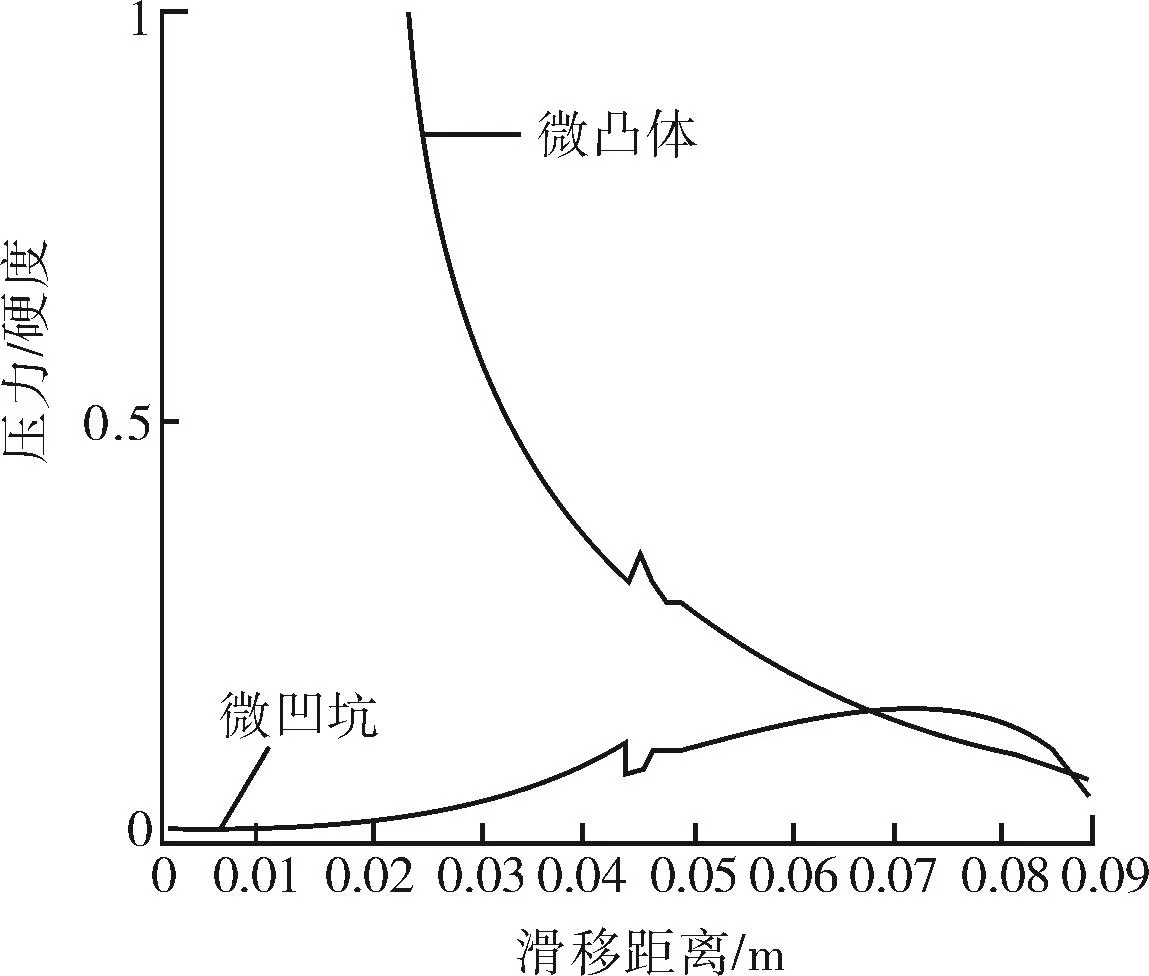
图4 微凸体压力、微凹坑压力与滑移距离的关系曲线
微凸体接触压力和微凹坑油层压力随滑行距离的关系,起始阶段前者压力显著高于后者,但随着滑移距离的增大,微凸体被逐步磨平,微凸体接触压力逐步降低,并且随着这一过程更多的油层被泄露出去,从而油层压力逐步提高,直到大约滑移距离超过0.072 m时,油层压力高于微凸体压力。
摩擦磨损过程中微观形貌与滑移距离的关系曲线如图5所示。反映了随着磨损的进行,微观形貌的变化趋势。图5a为微凸体被逐步磨平的过程,磨损进行到一定程度后,微凸体高度变化的速度逐步降低,最后趋于平稳;图5b表示随着滑移距离的增大,由于微凸体高度降低,实际接触面积比逐渐增大,并最终趋于平稳。在磨损开始前,表面认为是各向异性的,此时可认为Peklenik因数γ约为3;磨损后,表面的同质化更明显,因而Peklenik因数γ在磨损后逐渐趋向于1。
仿真得出的表面粗糙度Rq随滑移距离的变化曲线如图 6所示。随着磨损的进行,微凸体高度逐步降低,因此表面粗糙度也随之降低,因此称之为“磨损抛光效应”。根据仿真的结果,Rq由起始的2.8 μm下降到最终稳定时的约1.1 μm,这是因为微凸体磨损导致微凹坑中的油压上升,从而抑制了微凸体的进一步磨损,最终Rq相对稳定。
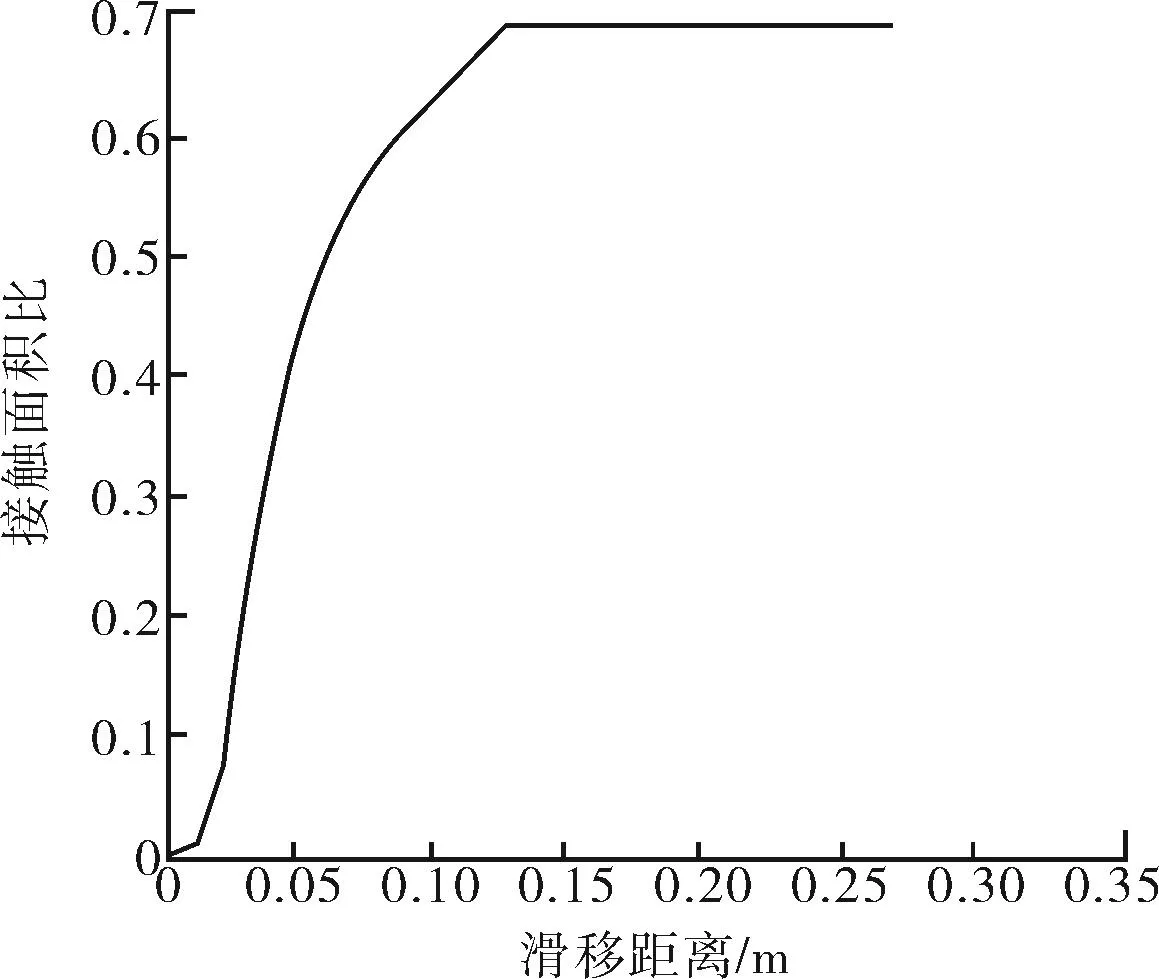
b 接触面积比
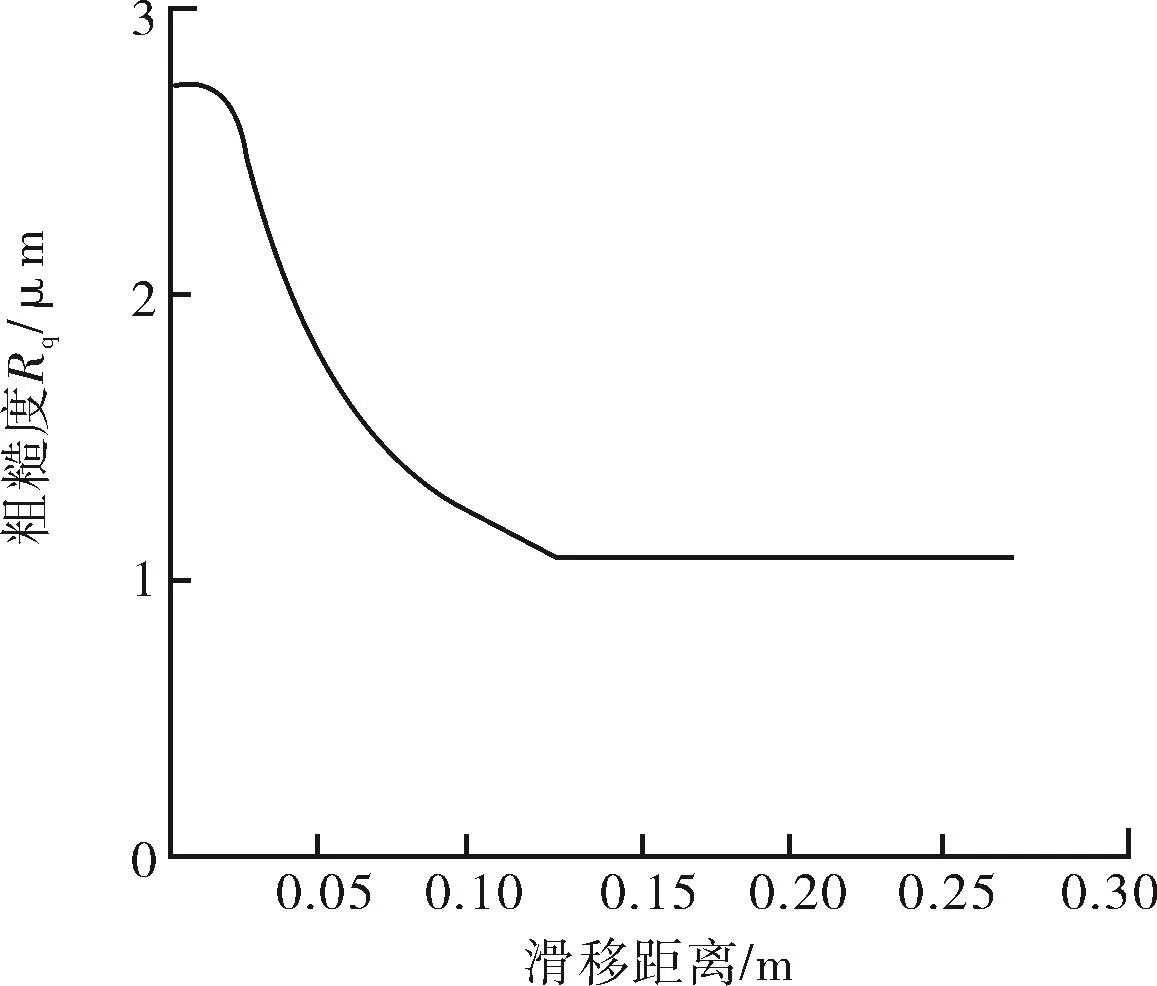
图6 摩擦磨损过程中表面粗糙度与滑移距离的变化曲线
3摩擦模型
Sutcliffe等人[41]分析了粗糙表面间相对运动时,表面参数与各压强的关系。滑移过程中微凹坑及压力分布的变化如图7所示。
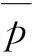
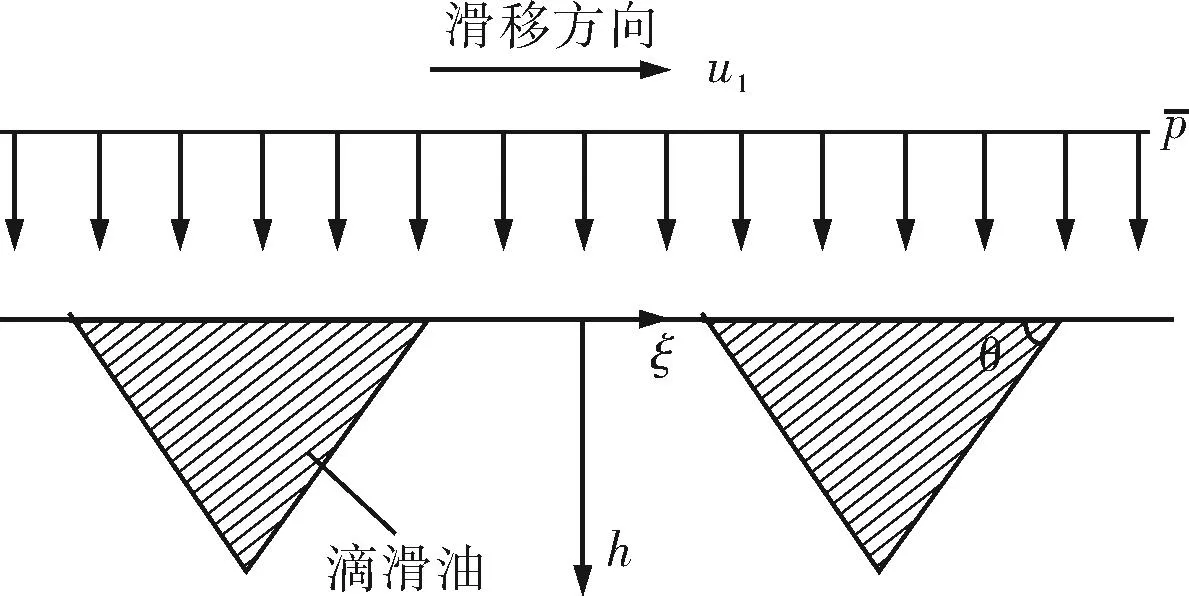
a 微凹坑在独立状态下受均匀压强作用
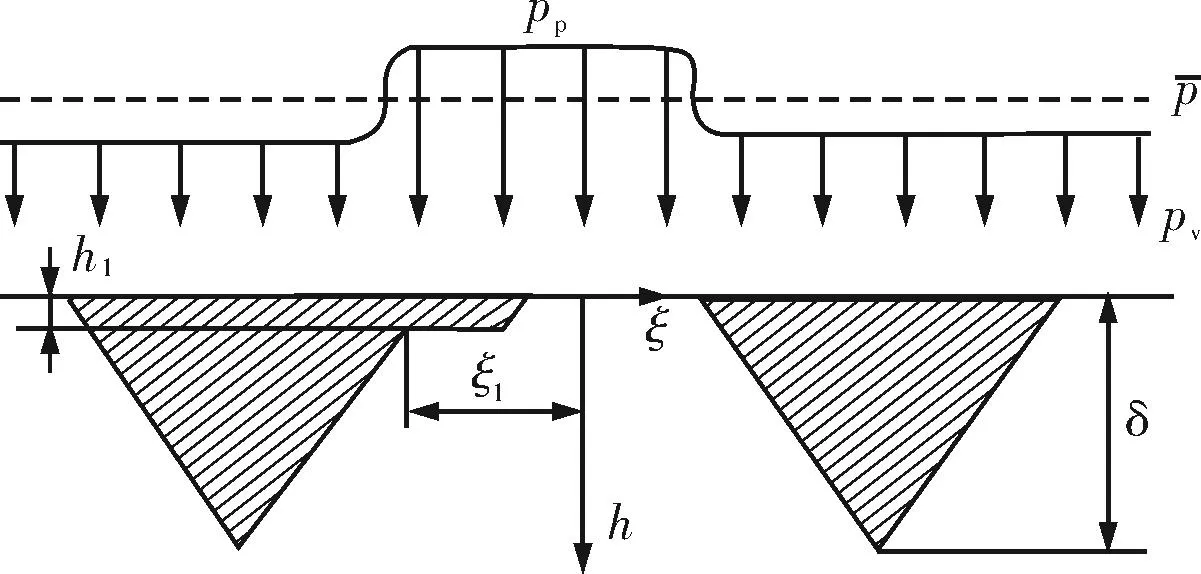
b 摩擦磨损下润滑油重新分布导致的压强分布
根据Sutcliffe等人[41]的推导,填充部分的油层厚度h1为
(17)

摩擦因数由微凸体上的摩擦因数与微凹坑内油层的摩擦因数2部分组成。由于油层摩擦因数较微凸体上的摩擦因数很小,可忽略不计。
μ=Apμp
(18)
式中:μp为微凸体上的摩擦因数,由金属对金属的直接接触摩擦和带薄膜润滑的边界润滑摩擦2部分组成,二者的权重分别是2种摩擦对应的面积比率Ar和1-Ar,因此:
μP=Arμb+(1-Ar)μv
(19)
式中:Ar同时取决于润滑油的厚度和表面粗糙度;μb是金属对金属摩擦因数,为常数;μv为边界润滑部分的摩擦因数,通过Eyring方程进行计算。
(20)
式中:τ0为Erying润滑剪切应力;h1为填充部分的油层厚度,h1远小于微凹坑的纵向深度δ。
为更好地贴近实际工况,还需做进一步简化与假设。第一,假设滑移过程中的磨损是适度的,既不过于严重,也不过于温和,前者对应的磨损因数k大约在1×10-6量级,后者对应k在1×10-2量级,本文取k=3×10-4。第二,假设金属对金属摩擦因数μb为0.6[22]。第三,假设螺纹脂的黏度约为50 Pa·s。第四,Erying润滑剪切应力取值2 MPa[42]。第五,微凸体面积率Ap、接触半径R、维氏硬度H、微凹坑角度θ等值均取自实际试验的观测结果[38]。第六,承载载荷W、工件表面粗糙度Rq、滑移速率v作为本文研究的变量,通过选取不同的值考查这些参量变化对摩擦因数的影响。仿真模型参数如表 1所示。
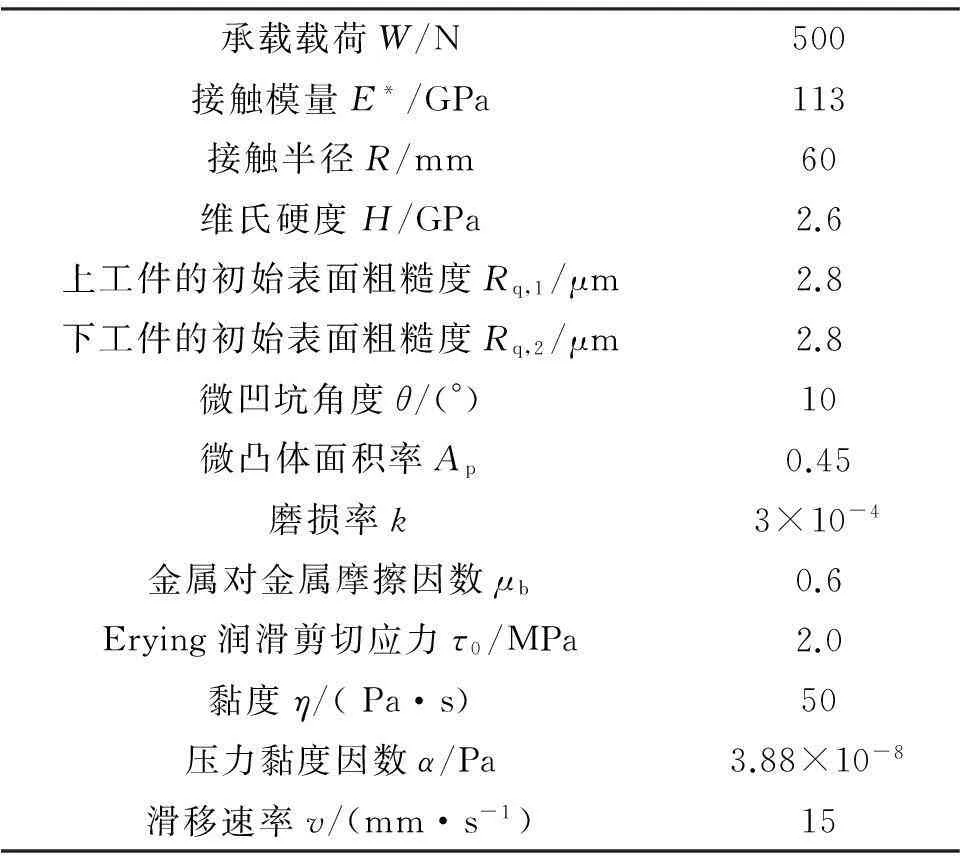
表1 仿真模型参数
经过仿真计算,滑移过程中摩擦因数的变化趋势如图 8所示。经过约0.1 m的滑移距离,摩擦因数由最初的0.17下降到0.15,下降率约为12%,随后摩擦因数稳定在0.15附近。
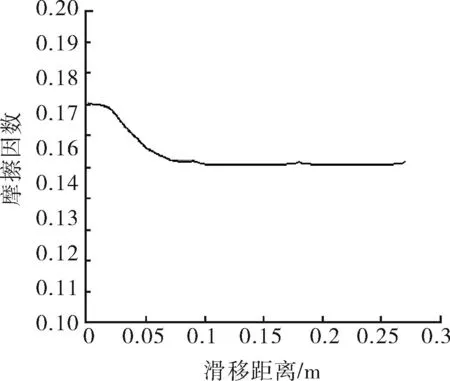
图8 滑移过程中摩擦因数的变化趋势
综上所述,本文基于一定的模型简化,根据基于表面粗糙度的微凹坑润滑模型,估计了微凸体接触面积,进而计算了摩擦因数的值,并给出了伴随着上扣过程中微凸体磨损导致的摩擦因数的变化趋势,仿真结果与实际试验结果的趋势一致。
4结论
1)摩擦因数的大小对于计算合理的上扣转矩是非常重要的,而摩擦因数的数值取决于复杂的摩擦磨损系统,这一系统中任何微小变量的改变都将造成摩擦因数的变化。
2)API虽然给出了摩擦因数的推荐值,但API对该推荐值过于简化,不同表面特性、不同材料下的摩擦因数都认为是一致的,并且在后续第2次乃至多次上扣过程中,该值也被认为是常数,因此推荐上扣转矩也是恒定的。不同的润滑状态、接触压力、上扣速度、上扣次数、表面性能以及润滑脂的性能都会对摩擦因数产生影响,上扣转矩的推荐值也存在一定偏差,在实际操作中存在转矩过大或转矩不足的风险。
3)同样的工况下,摩擦因数并不是恒定不变的,它受到多方面的影响,且随上扣过程逐步下降。在本算例中,经过约0.1 m的滑移距离后,微凸体高度逐步下降,接触面积比随之增高,表面粗糙度从起始的2.8 μm下降到约1.1 μm;在这个过程中,摩擦因数由起始值0.17下降到稳定值0.15。这是由于在上扣过程中,“磨损抛光效应”导致了表面粗糙度的降低,从而获得了更好的润滑条件。
4)不论是API标准,还是各特殊螺纹生产商,都应核实更精确的摩擦因数,从而确保上扣转矩值的合理计算。此外,除了本文考虑的诸多因素外,还有其他环境变量也会影响摩擦因数的大小,例如上扣现场的环境温度也会对摩擦磨损系统产生影响,这也应当纳入未来的研究方向。
参考文献:
[1]吕拴录,韩勇,赵克枫,等.特殊螺纹接头油套管使用及展望[J].石油工业技术监督,2000,16(3):1-4.
[2]付彧,齐国权,卫遵义,等.特殊螺纹油套管设计及国内产品现状[J].石油矿场机械,2012,41(10):72-76.
[3]何牛仔,高学仕,李兆勇.热采井套管螺纹连接有分析[J].石油矿场机械,2007,36(9):64-66.
[4]Guangjie Y,Zhenqiang Y,Qinghua W,et al.Numerical and experimental distribution of temperature and stress fields in API round threaded connection[J].Engineering Failure Analysis,2006(13):1275-1284.
[5]Schwind B. Mobil qualifies three tubling.casing connection product lines[J]. Hart's Petroleum Engineer International,1998(4):59-62.
[6]Cuvalci O,Sofuoglu H,Ertas A.Effect of surface coating and tin plating on friction characteristics of P-110 tubing for different thread compounds[J].Tribology International,2003(36):757-764.
[7]Kent S,Amiel G,Faucon B.North Sea Gas Leak Could Cost Billions[N].The Wall Street Journal,2012.
[8]Van W J,De Pauw J,De Baets P,et al.Fatigue investigation of threaded pipe connections[J].Sustainable Construction & Design,2010(2):182-189.
[9]Galle T,De Waele W,De Baets P,et al. Influence of design features on the structural integrity of threaded pipe connections[J].Sustainable Construction and Design 2011,2(2):237-245.
[10]Bradley A B,Nagasaku S,Verger E.Premium Connection Design,Testing and Installation for HPHT Sour Wells[C]//Texas:SPE High Pressure-High Temperature Sour Well Design Applied Technology Workshop,2005.
[11]Van Wittenberghe J,De Pauw J,De Baets P,et al.Experimental determination of the fatigue life of modified threaded pipe couplings[J].Procedia Engineer,2010,2(1):1849-1858.
[12]De Baere I.Design of a three-and four-point bending setup for fatigue testing of fibre-reinforced thermoplastics[G].2001.
[13]API RP 5C5(ISO 13679),Recommended Practice on Procedures for Testing Casing and Tubing Connections[S].2003.
[14]王少兰,费敬银,骆立立,等.石油钻具螺纹防粘扣技术及应用[J].电镀与精饰,2014,36(1):18-22.
[15]张永强,王新虎.油套管螺纹抗粘扣技术研究进展[J].石油矿场机械,2008,37(2):78-81.
[16]Duggan T V.Applied engineering design and analysis[M].1st Edition ed,London:Iliffe,1969.
[17]API RP 7G,Recommended Practice for Drill Stem Design and Operation Limits 16th Edition.American Petroleum Institute[S].2009.
[18]API RP 5A3 (ISO 13678),Recommended Practice on Thread Compounds for Casing,Tubing,Line Pipe,and Drill Stem Elements[S].2009.
[19]陈守俊,高连新,张毅,等.油套管螺纹联接粘扣失效过程的试验研究[J].华东理工大学学报(自然科学版),2012,38 (2):247-251.
[20]Bezensek B.Finite Element Analysis of the Seal During Make-up[M].2010.
[21]Bengisu M T,Akay A.Stick-slip oscillations:Dynamics of friction and surface roughness[J].Journal of the Acoustical Society of America,1998,105(1):195-204.
[22]温诗铸,黄平.摩擦学原理[M].北京:清华大学出版社,2008.
[23]Heide E V,Schipper D J.Galling initiation due to frictional heating[J].Wear,2003 (254):1127-1133.
[24]Coulomb C A.Memoires de Mathematique et de Physique de l'Academie Royale des Sciences [M].Theorie des machines simples,Paris:Academie Royale des Sciences,1985.
[25]Nayak P R.Random process model of rough surfaces[J].Journal of Wear,1973,26(3):305-333.
[26]Sedlacek M,Podgornik B,Vizintin J.Influence of surface preparation on roughness parameters,friction and wear[J].Journal of Wear,2009(266):482-487.
[27]Meng Q,Gao L,Liu F,et al. Contact mechanics and elastohydrodynamic lubrication in a novel metal-on-metal hip implant with an aspherical bearing surface[J].Journal of Biomechanics,2010(43):849-857.
[28]Shafiei M,Alpas A T.Effect of sliding speed on friction and wear behaviour of nanocrystalline nickel tested in an argon atmosphere[J].Journal of Wear,2008(265):429-438.
[29]Farhat Z N,Ding Y,Northwood D O,et al.Effect of grain size on friction and wear of nanocrystalline aluminium[J].Materials Science and Engineering,1996(A206):302-313.
[30]Kim H,Kardes N.Friction and lubrication[M].Altan T,Tekkaya A E,editors.Sheet Metal Forming-Fundamentals:ASM International,2012.
[31]Archard J F.Contact and Rubbing of Flat Surfaces[J].Journal of Applied Physics,1953(24):981-988.
[32]Le H R,Sutcliffe M P F.Rolling of thin strip and foil:application of a tribological model for "mixed" lubrication[J].Journal of Tribology,2002(124):129-136.
[33]温诗铸,黄平.界面科学与技术[M].北京:清华大学出版社,2011.
[34]Persson B N J.Elastoplastic Contact between Randomly Rough Surfaces[J].Physical Review Letters,2001,87(11):1-4.
[35]Christensen H.Stochastic model for hydrodynamic lubrication of rough surfaces[G].Proceedings of the Institution of Mechanical Engineers,1969-1970(184):25-1013.
[36]Williams J A.Engineering Tribology[M].Cambridge:Cambridge University Press,2005.
[37]Hamrock B J,Dowson D.Elastohydrodynamic Lubrication of Elliptical Contacts for Materials of Low Elastic-Modulus I-Fully Flooded Conjunction[J].J Lubric Tech-T Asme,1978,100(2):45-236.
[38]Stewart F,Le H R,Williams J A,et al.Characterisation of friction and lubrication regimes in premium tubular connections[J].Tribology International,2012(53):66-159.
[39]Patir N,Cheng H S.Average Flow Model for Determining Effects of 3-Dimensional Roughness on Partial Hydrodynamic Lubrication[J].J Lubric Tech-T Asme,1978,100(1):7-12.
[40]Li W L,Chein W T.Parameters for Roughness Pattern and Directionality[J].Tribol Lett,2004,17(3):51-547.
[41]Sutcliffe M P F,Le H R,Ahmed R.Modeling of micro-pit evolution in rolling or strip-drawing[J].Journal of Tribology,2001(123):33-40.
[42]Le H R,Sutcliffe M P F.A multi-scale model for friction in cold rolling of aluminium alloy[J].Tribol Lett.,2006,22(1):95-104.
Theoretically Modeling of Coefficient of Friction Influenced by Frictional Wear during the Make-up of OCTG
CAO Shan,GAO Jinwei,KONG Xiangling,DANG Min,YAN Baichen
(ChinaPetroleumTechnologyandDevelopmentCorporation,Beijing100028,China)
Abstract:A pre-defined torque value is required in the rig site operation for both the API and premium connections.The torque value is calculated using the coefficient of friction (CoF) between the two surfaces.However,the existing estimation to the CoF comes from empirical data and is usually considered as a constant.This may be inaccurate due to the variation of surface and operation conditions.Therefore,it might lead to over or under torque of the connections,especially in the high pressure high temperature wells.Therefore,a theoretical approach was taken to correlate the surface topography,roughness and CoF with sliding distance.Because of the micro burnishing during the make-up process,CoF is gradually reduced and be steady at about 88% of the initial value.The results help to understand how friction is related to external circumstances in the operation of OCTG connections.
Keywords:OCTG;torque;thread;coefficient of friction
中图分类号:TE931.2
文献标识码:A
doi:10.3969/j.issn.1001-3482.2016.03.006
作者简介:曹杉(1986-),男,北京人,主要从事油井管研究,E-mail:caos@cptdc.cnpc.com.cn。
收稿日期:①2015-09-29
文章编号:1001-3482(2016)03-0025-08

