基于支持向量机模型的滚动轴承运行状态预测研究
赵占飞,梁 伟,郭晓燕
(中国石油大学(北京) 机械与储运工程学院,北京 102249)①
基于支持向量机模型的滚动轴承运行状态预测研究
赵占飞,梁伟,郭晓燕
(中国石油大学(北京) 机械与储运工程学院,北京 102249)①
摘要:为了提高支持向量机对滚动轴承运行状态预测的准确性,采用遗传算法对支持向量机的核参数与惩罚因子进行优化,选取最优支持向量机参数;研究了时间序列预测中嵌入维数对预测精度的影响,提出了嵌入维数优选-参数优化支持向量机预测模型。通过轴承寿命加速试验表明,该模型可以提高滚动轴承运行状态预测的准确性,达到轴承故障预警时间预测的目的。
关键词:轴承;支持向量机;参数优化;状态预测
滚动轴承是各类石油石化旋转机械中应用最为广泛的一种零部件[1]。滚动轴承由于其本身结构特点,会承担一定负载并以一定速度旋转,同时还需承受外部因素所产生的激励,滚动轴承极易发生故障。据统计资料表明,在使用滚动轴承的旋转机械中,约有30%的机械故障是由滚动轴承引起的[2]。以滚动轴承历史样本数据为基础,对其进行运行状态预测研究,推测其发展劣化趋势,对提高设备安全运行具有重大意义。
在状态预测方法研究中,支持向量机(Support Vector Machines,SVM)以其具有逼近任意复杂系统的能力与先进的完备理论而受到广泛应用[3]。支持向量机核参数γ与惩罚因子C的选取对预测结果影响很大[4]。对于支持向量机参数优化问题,较为常用有以下几种方法:粒子群优化算法(Particle Swarm Optimization,PSO)寻优[5];遗传算法(Genetic Algorithm,GA)寻优[6];网格搜索法(Grid Search,GS)寻优。网格搜索法通过对一定空间范围划分网格,遍历网格中所有点寻优,若网格步长足够小,该方法可寻得最优参数,但其运算时间较长;遗传算法属于启发式算法,寻优速度快,具有很强的全局优化搜索能力;粒子群优化算法与遗传算法相似,其算法规则更为简单,求解速度快,但其收敛性理论方面仍有待完善[7-8]。
由Takens定理[9]可知,在利用机器学习方法对时间序列进行预测中,序列嵌入维数m会对预测结果产生影响,m值过大与过小均会造成预测结果产生较大的偏差。目前主要由工程经验来选取嵌入维数的方法缺乏推广性与合理性[10-11]。
本文提出嵌入维数优选-参数优化支持向量机预测模型,对时间序列嵌入维数进行优选,实现嵌入维数选取自适应性;对支持向量机核参数γ与惩罚因子C采用理论基础较为成熟的遗传算法进行参数寻优。并用滚动轴承寿命加速试验数据进行方法研究,试验结果表明,该模型可以准确预测出滚动轴承的运行状态与劣化趋势,以及轴承故障的预警时间;为滚动轴承设备的科学管理提供依据。
1优化支持向量机模型
1.1支持向量机
支持向量机是由Vapnik所提出的一种以统计学习理论(Statistical Learning Theory,SLT)为基础的新型通用机器学习方法[12]。支持向量机适用于小样本数据的分类或回归计算。对于预测问题,支持向量机采用回归算法;基本思想是通过一个非线性映射将输入空间映射到高维特征空间中进行回归,确定其映射函数,从而得到未知样本取值[13]。
在支持向量机回归运算中,给定样本数据{xi,yi},i=1,2,…,n;其中{xi}为输入序列,{yi}为输出序列。支持向量机回归运算本质为解二次优化问题,其运算过程如文献[13],可得优化目标为
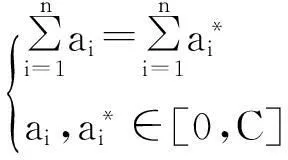
(1)

依据KKT条件,可求得上式中各参数,支持向量机回归函数为
(2)
对于某一时间序列X={xn-m,xn-m+1,…,xn-1},输出为Y={xn};支持向量机预测模型使X与Y形成Rm→R的映射关系,其中m为时间序列X的嵌入维数,X与Y的训练样本为[14]
(3)
依据支持向量机回归函数式(2),可得该样本回归函数为
(4)
由式(4)可得第n+1点预测值为
(5)
将第n+1点的预测值作为输入值,更新输入样本时间序列向量X,重新进行支持向量机回归计算,可求得第n+2点的预测值。同理依次可求得第n+3,…,n+s点预测值。
1.2嵌入维数优选
在相空间重构理论中,嵌入维数m的选取对时间序列预测结果的准确性影响很大;若m太小,则不能够展示复杂行为的细致结构,若m太大,则会使计算工作复杂化[14-15]。时间序列预测模型性能评价有多种指标,其中相关系数平方(Squared Correlation Coefficient,SCC)应用较为广泛。相关系数平方描述了预测值与实际值之间的相似程度,其值越大表征预测结果越好,其计算公式为[11,16]
(6)

1.3SVM参数优化
支持向量机模型通过核函数的引入使得运算过程中内积不必在高维空间中计算,避免了维数灾难。支持向量机有多种核函数,其中径向基函数应用比较广泛,其形式为[13]
K(xi,xj)=exp(-γ‖xi-xj‖2)
(7)
式中:γ为核函数参数。
在支持向量机算法中,核函数参数γ与惩罚因子C是影响支持SVM算法的复杂程度与回归分类性能的关键参数。目前对于支持向量机参数优化问题,较为常用算法有网格搜索法寻优[17],粒子群优化算法寻优[18],遗传算法寻优。本文采用理论基础较为成熟的遗传算法进行参数寻优。
遗传算法(GA)是一种模拟生物进行的智能优选算法,具有广泛适用性的全局寻优能力[19]。它的算法过程与粒子群优化算法类似,但其具体运算法则更为复杂。其基本过程如下:①初始化。初始化(γ,C)的取值范围,随机产生初始群体,并对群体中的个体参数进行二进制编码;②适应度计算。采用交叉验证算法计算各个体的预测均方误差值作为适应度值;③遗传运算。对群体进行选择、交叉、变异运算,产生下一代群体;计算新一代群体的适应度值。循环迭代进行遗传过程,直至群体性能满足最优准则,结束计算。进行解码运算最终可得最优SVM参数(γbest,Cbest)。
1.4优化支持向量机模型算法
本文将嵌入维数优选、支持向量机参数优化相结合,提出了嵌入维数优选-参数优化支持向量机预测模型。
第1步。为确保训练过程精度,首先将实际时间序列X进行归一化处理。
第2步。依据工程经验,粗略选定支持向量机的核函数参数γ与惩罚因子C,进行回归运算;计算相关系数平方R2值,确定时间序列X的最佳嵌入维数。
第3步。采用遗传算法寻优,初始化支持向量机核参数γ与惩罚因子C的搜索区间,产生初始群体并进行个体编码;采用交叉验证算法计算预测均方误差值(MSE)作为适应度值,直至最终确定最优支持向量机参数(γbest,Cbest)。
第4步。以已确定最佳嵌入维数的时间序列X为输入序列,采用最优参数支持向量机进行回归计算得到预测时间序列Y,并对其进行反归一化处理。
2试验研究
2.1试验简介
试验数据由ABLT-1A型滚动轴承寿命加速试验平台(如图1)所采集。试验平台由电动机-皮带轮驱动,主轴转速为3 000 r/min,同轴安装滚动轴承。轴承振动信号由轴承箱外部安装的一个加速度传感器采集。该平台每隔1 min对轴承运行振动信号进行一次采集,采样频率为20 kHz。滚动轴承所承受的载荷由砝码-油压放大系统加载。试验过程中,砝码与托架的总质量为17.7 kg,油压系统的放大倍率为100,滚动轴承最终承受的径向载荷为8.67 kN。

图1 滚动轴承寿命试验平台
试验开始时,滚动轴承均完好无损,随着运行时间增加滚动轴承会出现故障征兆且最终失效,且振动烈度在出现故障征兆时会大幅度增加。分别采用最终轴承失效形式为内圈点蚀、滚动体故障(如图2所示)的试验数据进行状态预测计算。取滚动轴承振动烈度值作为反映轴承运行状态的参数。本文数据为2次轴承寿命加速试验过程中末期56 h(此时间段包括轴承正常运行、轴承出现故障征兆、轴承故障3种不同状态)的数据,通过传感器所采集的数据计算轴承每小时的振动烈度平均值,分别得到2次试验的连续56 h的烈度值序列。将最终失效形式为内圈点蚀的试验烈度值序列编号为序列A,最终失效形式为滚动体故障的试验烈度值序列编号为序列B。

a内圈点蚀 b滚动体故障
图2最终轴承失效形式
2.2数据分析
为确保运行结果准确性,首先对样本点数据进行归一化处理。按照工程经验以及文献试验数据,先粗略选定支持向量机核函数参数γ=0.5,惩罚因子C=5。时间序列嵌入维数范围为[3,10]。采用样本时间序列A、B进行计算,得到相关系数R2值,如图3所示。

图3 嵌入维数-相关系数平方值
由图3可知,序列A与序列B的最优序列嵌入维数均为6,即式(3)中训练样本X的m值为6。本文分别对A、B两组序列的样本点进行状态预测计算,因此在对每组序列预测前均需进行参数寻优。遗传算法寻优参数设置如下:采用均匀设计方法[20]初始化GA参数,径向基核函数参数范围置为[0,1000],惩罚因子参数范围置为[0,100];种群最大数量为20,最大进化代数为200;采用5折交叉验证计算适应度值(MSE),寻得最优参数。寻优结果如表1所示。

表1 GA算法寻优结果
依据表1所确定的最优惩罚因子C与核函数参数γ,采用参数优化SVM预测模型对样本点数据进行状态预测计算。取A、B两组序列中前30个烈度值样本点作为训练数据,后26个烈度值样本点作为预测检验数据。依据标准ISO—10816,划定滚动轴承运行状态故障预警值=2×正常值;其中正常值取两组序列中前30个烈度值样本点的算术平均值。经计算,序列A预警值为17.52 mm/s,序列B预警值为10.78 mm/s。
为体现本文所使用的预测模型的优势,同时采用遗传算法参数优化SVM预测模型、常规SVM预测模型对样本点进行预测。遗传算法参数优化SVM模型只对SVM参数进行优化,不进行嵌入维数优选。常规SVM预测模型的核函数参数γ,惩罚因子C,嵌入维数依据工程经验分别置为0.5、5、3。预测结果如图4、表2所示。
如图2所示在试验过程中,序列A(轴承最终失效形式为内圈点蚀)中第1~51 h为正常运行状态,第52 h出现故障征兆,第53 h出现故障;序列B(轴承最终失效形式为滚动体故障)中第1~52 h为正常运行状态,第53 h出现故障征兆,第54 h出现故障。

a 序列A

b 序列B

预测模型序列A预测结果MSE值序列B预测结果MSE值嵌入维数优选-GA参数优化SVM模型0.15230.0062GA参数优化SVM模型0.59110.3531常规SVM模型1.04950.9270
通过对比表2中3种不同SVM模型对序列A、B的预测结果MSE值可知,本文所提出的嵌入维数优选-参数优化SVM模型的预测结果最佳,MSE值最小,更接近于轴承运行状态的实际值;常规SVM模型的预测结果较差,与实际值存在较大偏差。
由图4序列A、B预测结果图可知,滚动轴承实际烈度值序列A、序列B分别在第53 h、第54 h时超过故障预警线,嵌入维数优选-参数优化SVM模型的预测结果与实际值相符,能够对轴承的故障状态预警时间做出准确预测。GA参数优化SVM模型的预测结果与实际值存在偏差,在2次试验中对预警时间的预测均延后了1 h,即不能准确地对滚动轴承的故障状态预警时间做出预测。常规支持向量机模型的预测结果与实际值偏差较大,无法对故障状态预警时间进行预测。
3结论
1)采用本文所提出的嵌入维数优选-参数优化支持向量机预测模型,依据相关系数平方值(SCC)选取最佳嵌入维数、采用遗传算法(GA)进行SVM参数寻优;可以提高滚动轴承运行状态预测的准确性,从而能够对滚动轴承的故障状态预警时间进行预测。实现机械设备故障的早期预警,从而避免恶性设备安全事故的发生。
2)在采用支持向量机算法对滚动轴承运行状态进行预测中,训练样本的嵌入维数选择会对预测结果产生影响。
3)采用遗传算法(GA)对支持向量机核参数γ与惩罚因子C进行参数优选,寻优结果比较稳定,同时可提高预测结果的准确性。
参考文献:
[1]胡爱军,马万里,唐贵基.基于集成经验模态分解和峭度准则的滚动轴承故障特征提取方法[J].中国电机工程学报,2012,32(11):106-111.
[2]朱可恒.滚动轴承振动信号特征提取及诊断方法研究[D].大连:大连理工大学,2013.
[3]孙忠林.基于支持向量机的矿山安全状态的预测技术研究[C]//沈阳:国际安全科学与技术学术研讨会论文集,2008:34-37.
[4]亢生彩.网格搜索法SVM参数优化在主扇风机故障诊断中的应用[J].煤炭技术,2015,34(1):295-297.
[5]Chou Juisheng,Cheng Minyuan,Wu Yuwei,et al.Predicting high-tech equipment fabrication cost with a novel evolutionarySVM inference model [J].Expert Systems with Applications,2011(38):8571-8579.
[6]García Nieto P J,Gonzalo E G,Alonso Fernández J R,et al.A hybrid PSO optimized SVM-based model for predicting asuccessful growth cycle of the Spirulina platensis from raceway experiments data.Journal of Computational and Applied Mathematics[EB/OL].[2015-01-09].http://dx.doi.org/10.1016/j.cam.
[7]王健峰,张磊,陈国兴,等.基于改进的网格搜索法的SVM参数优化[J].应用科技,2012,39(3):28-31.
[8]王健峰.基于改进网格搜索法 SVM 参数优化的说话人识别研究[D].哈尔滨:哈尔滨工程大学,2012.
[9]Takens F.Detecting Strange Attractors in Turbulence [C].New York:Spring-Verlag,1981(898):366-381.
[10]张弦,王宏力.嵌入维数自适应最小二乘支持向量机状态时间序列预测方法[J].航空学报,2010,31(12):2309-2313.
[11]李鹤,杨周,张义民,等.基于径向基神经网络预测的混沌时间序列嵌入维数估计方法[J].物理学报,2011,60(7):1-5.
[12]Cortes C,Vapnik V. Support vector Networks [J].Machine Learning,1995(20):273-297.
[13]徐小力,王红军.大型旋转机械运行状态趋势预测[M].北京:科学出版社,2011:146-156.
[14]郭磊,郭金茂,徐达,等.基于分形和支持向量机的装备技术状态预测模型[J].科学技术与工程,2009,9(17):5172-5175.
[15]陈丽琳.基于多嵌入维数的时用水量LSSVM组合预测[D].杭州:浙江大学,2013.
[16]Satar Mahdevari,Hamid ShirzadHaghighat,Seyed Rahman Torabi.A dynamically approach based on SVM algorithm for prediction of tunnel convergence during excavation [J].Tunnelling and Underground Space Technology,2013(38):59-68.
[17]Wang Jie,Du Hongying,Yao Xiaojun,et al.Using classification structure pharmacokinetic relationship(SCPR) method to predict drug bioavailability based ongrid-search support vector machine [J].ANALYTICA CHIMICA ACTA,2007(601):156-163.
[18]许志军.基于粒子群算法优化支持向量机的数控机床状态预测[J].现代制造工程,2011(7):46-49.
[19]张颖璐.基于遗传算法优化支持向量机的网络流量预测[J].计算机科学,2008,35(5):177-197.
[20]何大阔,王福利,贾明兴.遗传算法初始种群与操作参数的均匀设计[J].东北大学学报(自然科学版),2005,26(9):828-831.
Research on the Prediction of Rolling Bearings Running based on Optimized SVM
ZHAO Zhanfei,LIANG Wei,GUO Xiaoyan
(CollegeofMechanicalandTransportationEngineering,ChinaUniversityofPetroleum,Beijing102249,China)
Abstract:In order to improve prediction accuracy of rolling bearings running,genetic algorithm to optimize SVM parameter was used.By comparing the accuracy of this algorithm,the best SVM parameter finally was chosen.At the same time,considering the time series forecasting embedding dimension as the number of parameters that affect the prediction accuracy.In this paper,an embedding dimension best choice-parameter optimization support vector machine prediction model are proposed.Experiments show that the model can improve the accuracy of prediction of rolling bearings running,and achieve the purpose of the bearing fault warning time prediction.
Keywords:bearing;support vector machine;parameter optimization;state prediction
中图分类号:TE929
文献标识码:A
doi:10.3969/j.issn.1001-3482.2016.03.004
作者简介:赵占飞(1990-),男,河北张家口人,硕士研究生,主要研究方向为设备安全监测与故障诊断,E-mail:zhao_zhan_fei@126.com。
收稿日期:①2015-09-11 国家科技重大专项(2011ZX05055)
文章编号:1001-3482(2016)03-0016-05

