山区高等级公路网交通安全微观模糊评价模型
张天文
(长春工程学院学生工作处,长春 130012)
山区高等级公路网交通安全微观模糊评价模型
张天文
(长春工程学院学生工作处,长春 130012)
摘要:以某山区高等级公路网交通安全特性为研究对象,通过对公路交通安全影响因素及交通现状特性的调查、分析,结合实际道路交通状况和交通特点,建立了山区高等级公路网交通安全微观模糊综合评价模型,并利用实际算例对该评价模型进行了对比验证。结果表明,模型确定的重点路段与公安交通及公路管理部门所掌握的事故易发地点吻合性较好,说明该模型在实际操作中可行、有效,能准确、全面地反映出所研究路段的真实安全水平,为改善山区高等级公路网交通安全提供了参考对策。
关键词:公路网;交通安全;模糊评价模型;交通事故
0引言
随着公路通车里程和车辆保有量的急剧增长,随之而来的是交通事故数量的迅速增长,自1997年起,每年因道路交通事故而死亡的人数超过7万,而且数字连年攀升,历年交通事故带来的人员伤亡、财产损失的增长率均超过10%,几乎与经济增长率持平[1-2]。事实上,“交通安全”本身就是一个模糊的概念,其边界及外延也是模糊的。若从传统的数学意义上去理解,“交通安全”应当指遭受交通事故的概率为零,显然这是很难做到的。当面对“交通安全”这样一个“亦此亦彼”的模糊概念时,经典数学就显得无能为力了。评价本身是人的思维判断过程,每一个评价者都有自己的观点和思维方式,这就导致即使对于同一个客体,不同的评价者也会得出不同的结论[3-5]。在构造评价模型时,完全避免人的主观性几乎是不可能的,比较现实的办法是尽可能将多种有代表性的思维方式考虑进来,以减少主观片面性,因此建立交通安全的模糊评价模型是合理而可行的。
1模糊模型构建
道路交通安全系统是一个无法进行精确描述的复杂模糊系统,模糊理论为解决这类问题提供了3个十分有用的工具,即隶属函数、语言变量和模糊算子[6-7]。借助于隶属函数,可以合理地解决“安全”与“不安全”概念之间的过渡[8],而不必像经典数学那样,硬性地规定一个绝对的界限;语言变量的引进使评价结果以模糊化的语言表现出来,更符合人们自然语言的口语化习惯;不同的模糊算子反映不同的思维方式,若采用多个模糊算子,便能综合考虑多种不同的评价观点。
1.1数学模型描述
已知Q和K为有限集合,令:
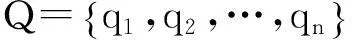
(1)
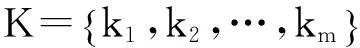
(2)
式中:qi(i=1,2,…,n)为集合元素,表示不同的被评价对象;kj(j=1,2,…,m)为集合元素,表示不同的评价指标。
令uj为第j个评价指标kj∈K的隶属函数,即
uj=μ(kj) uj∈[0,1],
则U为一个有限模糊子集,即

(3)
要寻求一个模糊集合B,则
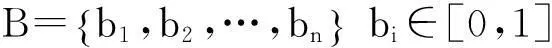
(4)
B中的元素bi表示第i个被评价对象的综合评价指数。
由于隶属函数uj适用于所有的评价对象qi,则可得到一个评价关系矩阵R,即
(5)
式中rji=R(uj,qi)∈[0,1],表示第j个评价指标适用于第i个被评价对象的隶属度。
定义S=(Q,U,R)为第一级评价空间,并给定一个模糊向量A,则
A=(a1,a2,…,am),
(6)
式中元素aj表示各评价指标关于第一级评价的相对重要程度系数。
因此,当模糊向量和模糊关系矩阵已知时,作模糊变换来进行综合评判。
B=A∘R=(b1,b2,…,bn),
(7)
式中 “∘”表示一种算法。
B中的各元素bi是在广义模糊合成运算下得到的运算结果,其计算式为
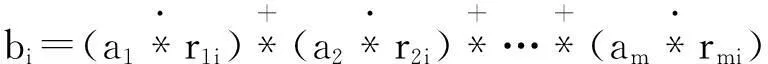
(8)
就理论上而言,广义模糊合成运算有无穷多种,但在本评判方法中,考虑各评价指标在评判中的地位无显著差异,为使模型简化,具体采用以下3种:
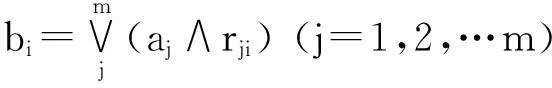
(9)
即综合评判结果为
B=(b1,b2,…,bn)=
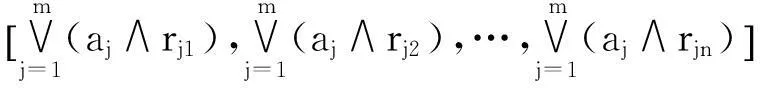
(10)
取:a1=a2=…am=1.0。
2) 模糊算子2:M(乘幂,∧),即
(11)
即综合评判结果为
B=(b1,b2,…,bn)
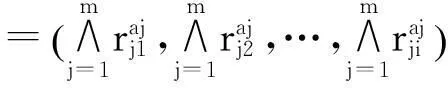
(12)
取a1=a2=…am=1.0。
3) 模糊算子3:M(·,+),即:
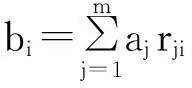
(13)
(14)
因此,得到3种简化综合评判模型为
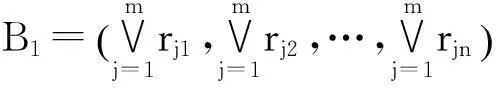
(15)
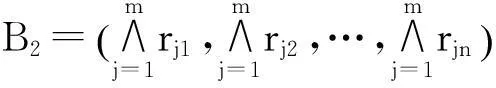
(16)

(17)
在采用简化模型作评判时,相当于对各对象的特性指标分别取最大值、最小值和平均值作为评价指标。在实际应用中,如果仅仅取最大值、最小值或平均值之一作为评价指标,可能会有片面性。因此,可综合使用B1,B2,B3这3个指标,建立二级评判空间。
设评判指标集为
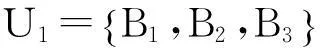
(18)
U1的各指标Bj(j=1,2,3)的权重分配为
(19)
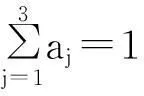
因此,评判指标集U1的总评判矩阵为:
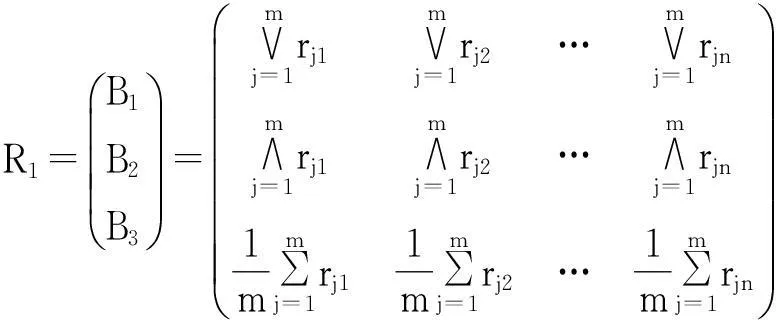
(20)
由此得出总的综合指标评判结果为
A1R1=B=(b1,b2,…,bn),
(21)式中左端是普通矩阵乘法,称bi(i=1,2,…,n)为二级评判指标,其中最大的bi值所对应的就是被评判的最佳对象的综合评价指数。特别指出的是,bi值的大小并不说明交通安全水平绝对意义上的高低。
权重向量中的元素表示3种模糊算子对的相对重要性,即最大值、最小值和平均值的权重分配,根据各模糊算子的运算特征,以及运算结果的“粗糙性”为参考,应用层次分析法,确定出权重向量中的元素。
在二级综合指标评价中,指标B1是从最突出的长处考虑问题,指标B2是从最突出的短处考虑问题,指标B3是从平均的角度考虑问题,这样更能融合多种评价者的思维方式,把乐观原则、悲观原则和平均原则的思维角度都加以考虑,最后又从综合的角度进行评价,这样使得最终评价结果更加合理,其实际上是强调了极值在评判中的作用和地位。
1.2隶属函数确定
隶属函数的作用不仅是将各指标转换为无量纲量,而且其取值本身也反映了交通安全水平的高低。为确定隶属函数需作如下基本假设:
1.2.1函数形式
评价指标kj的隶属函数uj∈[0,1]。隶属函数取降半柯西分布,即:
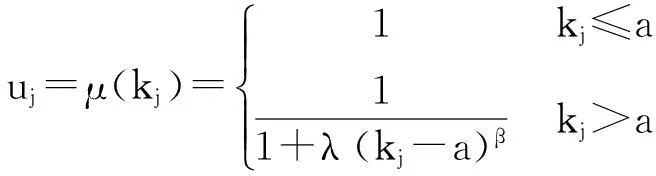
(22)
1.2.2抉择评语
每一评价指标可视为一个语言变量,其取值为一个有限集合V。
(23)
当vi=v4时,可认为此处为事故危险点。
1.2.3分布区间
集合V中的每一元素对应于隶属函数的可能性分布区间。
当vi=v4时,μj∈[0.00,0.50];
当vi=v3时,μj∈[0.50,0.65];
当vi=v2时,μj∈[0.65,0.85];
当vi=v1时,μj∈[0.85,1.00]。
因此,在kj-μj坐标中,存在一组临界值kjl(l=1,2,3,4),即μ(kj1)=1.00,μ(kj2)=0.85,μ(kj3)=0.65,μ(kj4)=0.50。
通过相关调查,采用模糊统计方法可得到各指标值的kjl,然后利用回归分析即能求出隶属函数的待定参数。
2模型算例
应用交通安全微观评价模型对某山区高等级公路网的部分路段进行安全性评价,依据一年的事故资料,从公路网中选取10个路段作为初始路段,通过对其进行安全评价,以确定出重点路段,初始路段对应的事故资料及交通量资料汇总见表1,对应的评价指标值见表2。
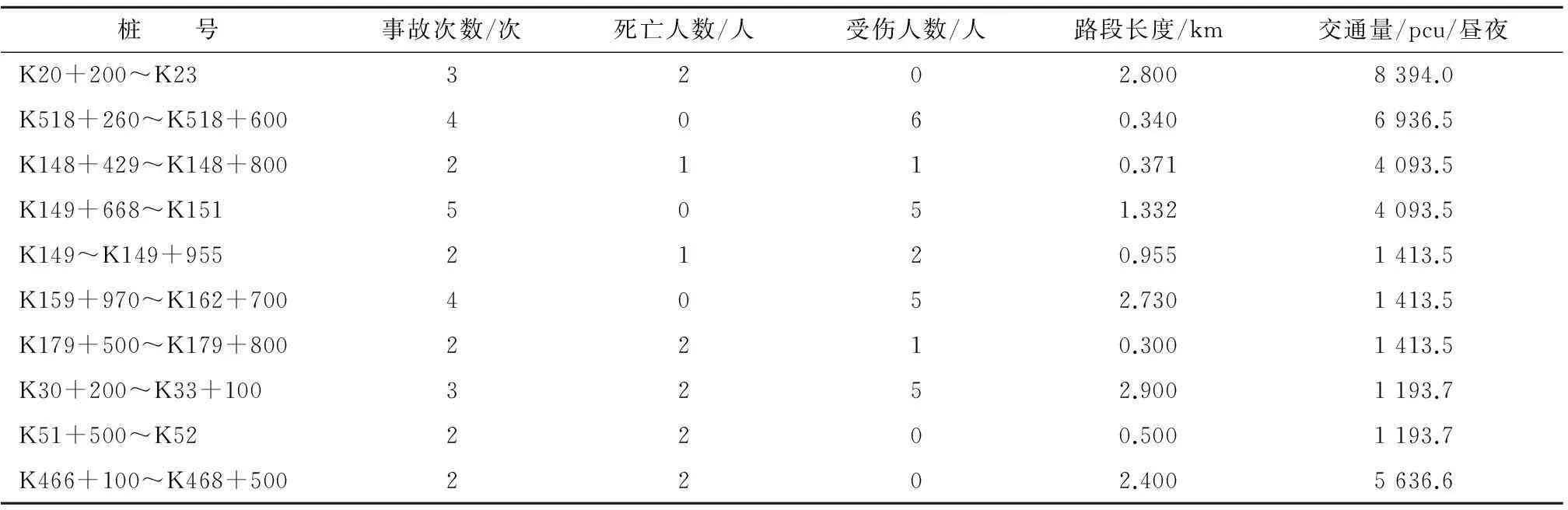
表1 初始路段的交通事故资料及交通量
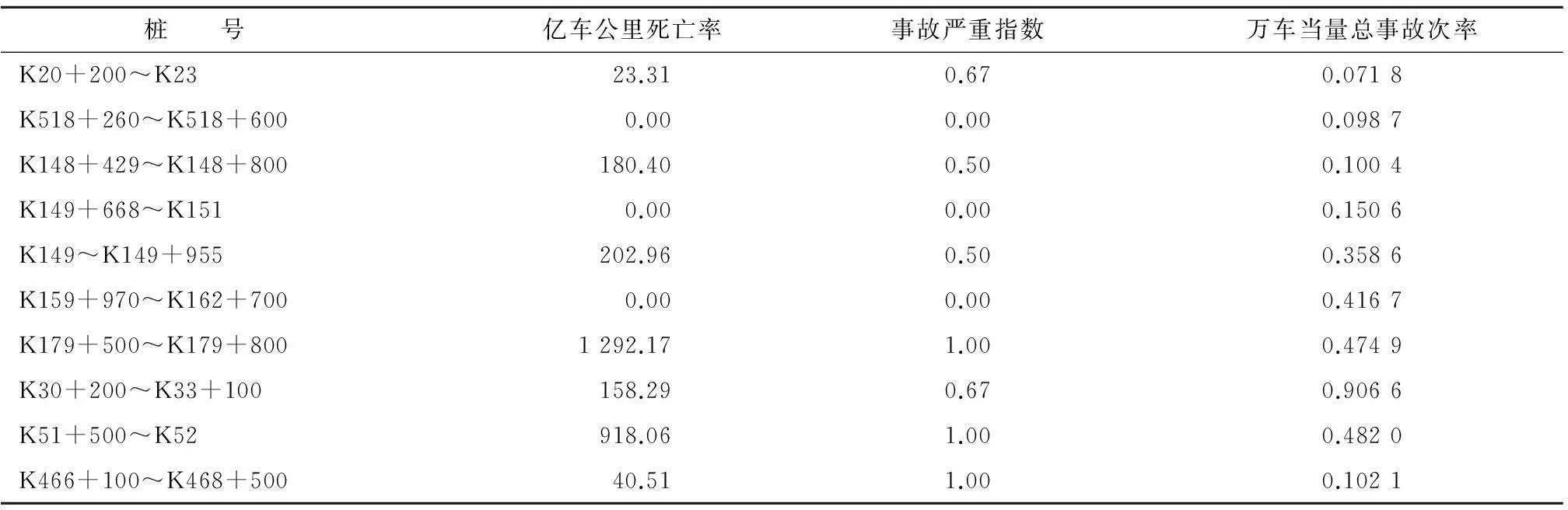
表2 10条公路评价指标值
通过对山区高等级公路安全状况的相关调查,采用模糊统计方法可以得到各指标的临界值,然后利用回归分析法计算出隶属函数的待定参数,见表3。

表3 隶属函数的参数值
应用模糊综合评价模型对10个路段进行评价,计算出路段的综合评价值,排序结果见表4。
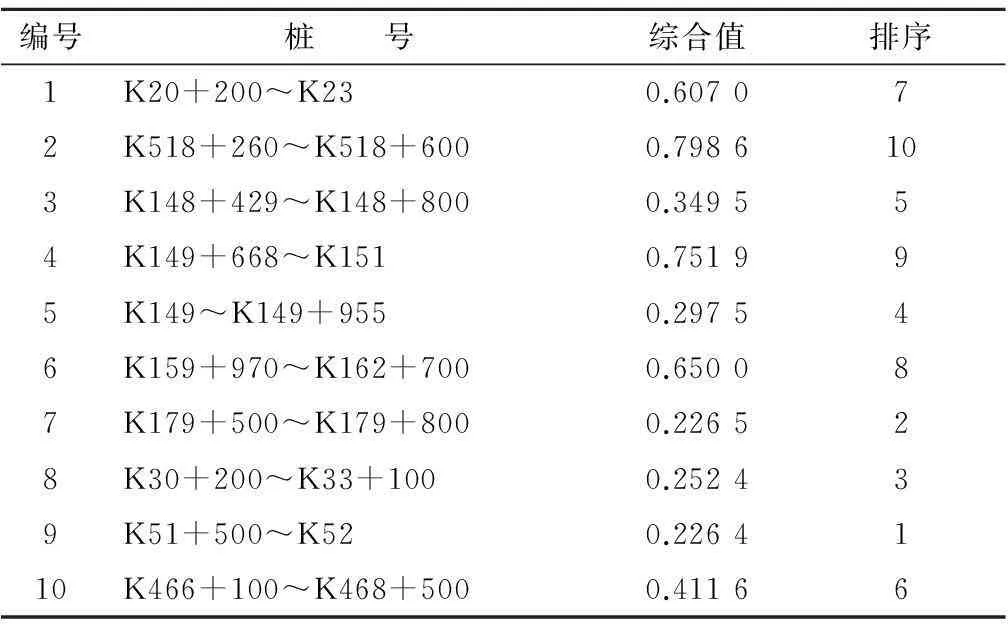
表4 10个路段的综合评价值
从表4可以看出,10个路段的综合安全水平存在明显差异,以0.5作为安全参考界限,可确定出交通事故重点路段,其编号为:9、7、8、5、3、10,这些路段的交通安全问题相对突出,可将其列为交通安全分析的重点。
3结语
建立了某山区高等级公路网交通安全微观模糊综合评价模型,应用模型确定的重点路段与公安交通、公路管理部门所掌握的事故易发地点相一致,说明评价模型在实际操作中是有效的。由于模型综合考虑了路段长度、交通量等因素,与管理人员主要侧重于事故发生的绝对数量相比,该模型所确定的重点路段,更能准确、全面地反映出路段的真实交通安全水平,而且以定量刻画的方式向管理人员描述了重点路段与正常路段之间以及重点路段之间的安全水平上的相对差异,为改善山区高等级公路网交通安全提供了参考依据。
参考文献
[1] 门玉琢,于海波,王华,徐亮.考虑驾驶员危险认知因素的山区弯路安全车速预测模型[J].机械设计与制造,2012,11:255-256.
[2] Rosenbloom T, Shahar A, Elharar A, et al. Risk perception of driving as a function of advanced training aimed at cognizing and handling risks in demanding driving situations[J]. Accident Analysis and Prevention, 2008, 40(2): 699-701.
[3] 邱安邦.道路交通安全的影响因素与综合评价[D].南京:南京林业大学,2008.
[4] 郑安文,牛倬民,郭健忠.高速公路道路因素与道路交通安全分析[J].武汉科技大学学报:自然科学版,2002,25(2):169-170.
[5] 李华成.高等级公路交通安全评价体系研究[D].长春:吉林大学,2007.
[6] Haglund M, Aberg L. Stability in drivers speed choice[J]. Ransportation Research Part F,2002, 5(3): 181-183.
[7] 徐晶. 高速公路交通安全微观评价方法及应用研究[D].北京:北京交通大学, 2011.
[8] Bins M, Graziano F, Bonino S. Risky driving and tyles in adolescence[J]. Accident Analysis and Perception, 2006, 38(3): 478-480.
The Study on Microscopic Fuzzy Evaluation Model of Traffic Security Based on Mountainous High-grade Highway Network
ZHANG Tian-wen
(DepartmentofStudentsAffairs,ChangchunInstituteofTechnology,Changchun130012,China)
Abstract:The traffic security features of a high-grade highway network are taken as the research object in this paper. Through the investigation, analysis of the factors impacting highway traffic security and the traffic status characteristics, combined with the actual road traffic conditions and characteristics, the microscopic fuzzy comprehensive evaluation model of high-grade highway network security has been established, and comparison validation of this model has been made by the use of a practical calculation example. The results show that the key road section determined by the model has a good consistency with the accident-prone locations mastered by the public security traffic and the highway management department. It indicates that this model is feasible, effective in practice, and can accurately and comprehensively reflect the true security level of the researched road section, which will provide some reference countermeasures to improve mountainous high-grade highway network traffic security.
Key words:highway network; traffic security; fuzzy evaluation model; traffic accident
文献标志码:A
文章编号:1009-8984(2016)01-0125-04
中图分类号:U492.8
作者简介:张天文(1982-),男(汉),吉林农安,硕士,讲师
基金项目:吉林省博士扶持项目(201603)
收稿日期:2016-02-20
doi:10.3969/j.issn.1009-8984.2016.01.028
主要研究可行性调研报告。

