姿态解算与外力加速度同步估计算法
孟唐宇 浦剑涛 方建军 梁岚珍


摘要:针对惯性导航应用中,姿态解算与外力加速度估计互相干扰的问题,提出一种基于四元数和扩展卡尔曼滤波器的姿态解算与外力加速度同步估计算法。首先,利用估计的外力加速度修正传感器加速度数据得到准确的反向重力加速度,再结合地磁场向量通过梯度下降算法解算得到旋转四元数的测量值;其次,构建扩展卡尔曼滤波模型,对旋转四元数和外力加速度进行更新,得到旋转四元数的预测值和外力加速度的预测值;最后,用旋转四元数的测量值和测量得到的加速度数据对预测值通过扩展卡尔曼滤波的方法进行校正,最终得到准确的旋转四元数和参考坐标系下三轴方向上的外力加速度。实验表明,通过扩展卡尔曼滤波同时对姿态和外力加速度估计的方法,能够迅速收敛并准确得机体姿态信息以及外力加速度信息,欧拉角误差为±1.95°,加速度误差为±0.12m/s2,并且该算法能有效抑制外力加速度对姿态解算的影响,准确估计外力加速度。
关键词:姿态解算;四元数;扩展卡尔曼滤波;梯度下降法;外力加速度
中图分类号:TP273+.5 文献标志码:A
Abstract:Aiming at the problem of mutual interference between attitude algorithm and external force acceleration estimation in inertial navigation system, a new method based on quaternion and extended Kalman filter was proposed. Firstly, the acceleration data of the sensor was corrected by using the estimated external force acceleration data to obtain the accurate reverse gravity acceleration, combined with geomagnetic field vector and calculated by the gradient descent algorithm, the rotate quaternions were obtained. Secondly, the extended Kalman filter model was constructed to update the rotate quaternions and external force acceleration, the prediction value of rotate quaternions and the external force were obtained. Finally, the measured values of rotate quaternions and the acceleration data were corrected by Kalman filtering method, the accurate rotate quaternions and the external force acceleration of the three axis directions in reference coordinate system were obtained. The experimental results show that the method for the synchronization estimation of attitude and external force acceleration by extended Calman filter can quickly converge and accurately get the information of the attitude and the external force acceleration, its Euler angle error is ±1.95° and acceleration error is ±0.12m/s2. The method can effectively restrain the influence of the external force acceleration on the attitude algorithm, and accurately estimate the external force.
Key words:attitude algorithm; quaternion; extended Kalman filter; gradient descent algorithm; external force acceleration
0 引言
在惯性导航应用中,如机器人、汽车产业和可穿戴设备等领域,常要求运动着的机体能够确定其自身当前的姿态,以及其外力加速度数据,来估算出机体的位置信息。目前常采用的方法是,用惯性测量传感器测量机体的惯性数据,通过算法解算出当前载体的姿态,再根据姿态信息解算得出外力加速度。
当机体加速移动时,外力加速度的存在会严重影响姿态解算的结果,当外力加速度越大时,求解的姿态角与实际值偏差越大。姿态解算算法主要有欧拉角法[1]、方向余弦法[2-3]和四元数法[4]等。欧拉角法是采用对反向重力向量的反三角函数求解的方法,虽然计算量小但存在万向节死锁问题;方向余弦法是通过旋转矩阵对载体坐标系进行转换,计算过程中要对旋转矩阵中的9个数据和传感器数据进行计算,所以计算量通常较大;四元数法相较于方向余弦法,采用四维数据进行计算,计算量大幅下降。在算法的运用中Wang等[5]运用四阶龙格库塔法和旋转矩阵的方法进行计算,并利用每次的计算结果来校正传感器的误差参数。这样虽然减小了计算量但是忽略了外力加速度对姿态的影响,实验结果可能会受到外力加速度的影响。Madgwick[6]运用梯度下降法解算载体姿态,这样计算在静态时准确度较高,但在动态时会产生姿态角的大幅抖动,并且过度依赖加速度计数据,使得外力加速度对计算姿态的影响更加明显。在算法的运用中如成怡等[7]利用非线性滤波,阎世梁等[8]运用互补滤波, Bachmann等[9]卡尔曼滤波,Madgwick等[10]运用梯度下降法, Marins等[11]利用扩展卡尔曼滤波算法。以上算法中为了消除外力加速度对姿态的影响,均将加速计传感器采集到的数据进行归一化,再进行姿态解算,这样可以减小外力加速度对反向重力向量的影响,但仍然没有从根本上消除外力加速度的影响,反向重力向量估计依然是不准确的。本文在姿态解算过程中,利用扩展卡尔曼滤波器模型,对姿态与外力加速度同步进行估计,不仅在姿态解算时消除了外力加速度对姿态解算精度的影响,同时可以得到外力加速度信息。
在外力加速度估计算法运用中张甜等[12]利用全球定位系统(Global Positioning System, GPS)基站方式进行加速度估计,如果在室内、地下室等GPS信号弱的环境下无法测量出机体的运动加速度。李海涛[13]利用电子罗盘修正加速度计信号的方法对机体外力加速度进行估计,然而电子罗盘信号容易受到外界电磁干扰,所得外力加速度会受到一定影响,因此姿态解算也会产生一定误差。
本研究采用基于四元数和扩展卡尔曼滤波器对机体姿态和外力加速度同时估计。利用外力加速度的估计值对采集到的加速度数据进行修正,得到修正后的反向重力加速度再结合磁场向量,采用梯度下降法估计出四元数测量值与加速度测量值;在此基础上,用扩展卡尔曼滤波器对预测四元数和预测外力加速度值同时进行修正,从而得到当前状态下机体准确的旋转四元数和参考坐标系下的外力加速度。
1 四元数介绍及基本运算
四元数应用在姿态解算中不仅计算量小还可以消除万向节死锁问题,并具有能够全角度解析姿态角等优点, 因此采用四元数作为姿态解算的数学推导演算依据。
1.1 四元数表示形式
对三角函数的±180°反解,得到姿态欧拉角的全角度解析,所得四元数为当前载体坐标系旋转到参考坐标系的四元数。从而有效解决欧拉角法产生的万向节死锁问题,同时减小运算量,并且提高运算速度。
2 扩展卡尔曼滤波姿态解算
为了预测非线性四元数和外力加速度值,引入扩展卡尔曼滤波器[11]。扩展卡尔曼滤波器能够预测出当前载体坐标系旋转到参考坐标系的旋转四元数和外力加速度,并通过测量值进行修正从而得到当前状态下准确的旋转四元数和外力加速度。这样计算得出的四元数不受外力加速度影响,计算出的姿态角在机体非匀速运动时波动小、外力加速度信息准确,同时分解出的外力加速度可用于惯性导航的研究。
扩展卡尔曼滤波姿态解算基本流程如图1所示。首先,利用陀螺仪数据更新旋转四元数,并且更新外力加速度数据;其次,估计预测协方差Pk以及扩展卡尔曼滤波增益K。再次,根据更新得到的旋转四元数计算载体坐标系下的反向重力向量;最后,根据测量值得到状态变量的最优估计并且更新协方差。其中xk表示状态变量,k表示当前状态,k-1表示上一时刻状态;Pk-1表示上一时刻协方差的值。
当前所得四元数,即为载体转向参考坐标系的旋转四元数,所得加速度为载体坐标系中三轴方向的加速度。通过四元数相乘的方法,把所得外力加速度转换成参考坐标系中三轴加速度,为实现惯性定位提供有效的加速度信息。
3 梯度下降法姿态解算
实际应用表明,仅把加速计采集到的数据作为反向重力向量,这样数据中隐含的外力加速度会影响旋转四元数测量值求解的准确度。为解决这一问题,先利用外力加速度的估计值修正加速计数据以得到准确的反向重力向量,再根据修正后的反向重力向量与磁场向量解算出测量四元数,从而减少外力加速度对旋转四元数的影响。
3.1 利用修正后的反向重力向量解算橫滚角和俯仰角
4 算法融合及实验结果分析
4.1 梯度下降法和扩展卡尔曼滤波融合
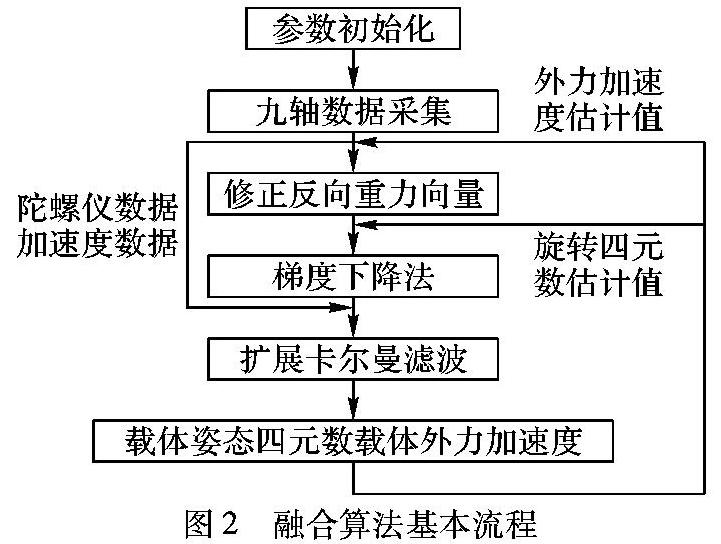
融合算法基本流程如图2所示。
梯度下降法循环计算2~3次,得到的四元数和加速计测值作为扩展卡尔曼滤波的测量值。融合算法结构如图3所示,其中Mag代表电子罗盘传感器所测量的磁场向量,Acc代表加速度传感器所测量的加速度向量,Gyr代表陀螺仪传感器所测量的角速度向量,acc代表计算得出的参考坐标系下机体外力加速度向量。
4.2 实验结果分析
实验MCU选用MEGA2560,传感器选用MPU6050、HMC5883L实验平台,MEGA2560以应答方式通过串口把九轴数据传送给Matlab进行实验仿真。传感器坐标系即为机体坐标系。
通过三种方式验证算法可行性和准确度。
1)机体处于水平位置。机体姿态模型如图4所示。所建模型和实物姿态一致。
机体处于水平位置未加扩展卡尔曼滤波与加上扩展卡尔曼滤波欧拉角对比曲线如图5所示,Pitch、Roll、Yaw角度在加入扩展卡尔曼滤波前后均稳定在0°,波动幅度±1.95°,但加入扩展卡尔曼滤波算法后角度波动幅度比未加入扩展卡尔曼滤波算法波动幅度有所减小。欧拉角波动是因为惯性传感器数据存在噪声引起,经过算法过滤后波动幅度减少了10%。在静止状态下两种算法解算出的欧拉角差别不大主要是应为没有外力加速度干扰。
机体向Y正方向以0.6m/s2匀加速运动,加入扩展卡尔曼滤波算法和未加入扩展卡尔曼滤波算法欧拉角对比曲线如图8所示,当机体做匀加速运动时,欧拉角曲线与机体静止时相比,加入扩展卡尔曼滤波算法的Roll有所减小,但范围在±0.5°,而没有加入扩展卡尔曼滤波算法的Roll减小了3°。外力加速度对加入扩展卡尔曼滤波算法姿态解算的结果影响很小而对未加入扩展卡尔曼滤波算法姿态解算影响较大。因机体处于水平位置,只在Y轴有一恒定加速度,Pitch和Yaw角度均稳定在0°,Yaw会随运动方向的误差有1°的变化波动。
3)机体在自由运动时,加入扩展卡尔曼滤波算法和未加入扩展卡尔曼滤波算法欧拉角对比曲线如图10,当机体处于自由运动时,加入扩展卡尔曼滤波算法与未加入扩展卡尔曼滤波算法姿态角曲线Pitch、Roll、Yaw角曲线趋势基本相同,但未加入滤波器的算法解算出的欧拉角均偏大,说明机体在自由运动时所产生的外力加速度对未加入滤波器算法的姿态解算产生较大影响,误差为±4.3°,而对加入滤波器算法的姿态解算影响较小,误差为±1.94°。
5 结语
本文在姿态解算与外力加速度同步估计中,基于四元数和扩展卡尔曼滤波器。通过对外力加速度的估计,修正反向重力向量,从而解算出旋转四元数的测量值,并利用卡尔曼滤波器对旋转四元数与外力加速度进行更新。这样减小了外力速度对姿态的影响,并且准确计算出姿态四元数和外力加速度。最后通过传感器采集数据解算当前传感器的姿态和加速度,验证了该方法的可靠性。在Matlab中姿态更新时间间隔在15ms左右,且采用应答方式获取传感器信息这会产生一定时间损耗。将算法移植到嵌入式系统中进行运算,这样不仅最大限度地降低数据在传输过程中产生的不必要的时间损耗,而且运算速度将大幅提升。现该算法已在室内定位小车项目中应用。
目前的研究比较集中于姿态的解算,尚未将外力加速度用于惯性导航中,这将是后续工作中要研究的一个重点工作。
参考文献:
[1]SUSHKOV O. Robot localisation using a distributed multimodal Kalman filter, and friends[D]. Sydney: University of New South Wales, 2006.
[2]PREMERLANI W, BIZARD P. Direction cosine matrix IMU: theory[EB/OL]. [2015-04-10]. http://gentlenav.googlecode.com/files/DCMDraft2.pdf
[3]周浩,浦剑涛,梁岚珍,等. 基于体感的仿人机器人步态学习与控制[J]. 计算机应用,2015,35(3):787-791.(ZHOU H, PU J T, LIANG L Z, et al. Gait learning and control of humanoid robot based on Kinect[J]. Journal of Computer Applications, 2015, 35(3):787-791.)
[4]KUIPERS J B. Quaternions and Rotation Sequences[M]. Princeton: Princeton University Press, 1999: 127-142.
[5]WANG Y, LI N, CHEN X, et al. Design and implementation of an AHRS based on MEMS sensors and complementary filtering[J]. Advances in Mechanical Engineering, 2014, 6(6): 1-11.
[6]MADGWICK S O H. An efficient orientation filter for inertial and inertial/magnetic sensor arrays[R/OL]. [2015-04-30]. http://www.xio.co.uklres/doc/madgwickinternaIJeport.pdf.
[7]成怡,金海林,修春波,等.四轴飞行器组合导航非线性滤波算法[J]. 计算机应用,2014,34(S1):341-344.(CHENG Y, JIN H L, XIU C B, et al. Nonlinear filter algorithm for quadrotor integrated navigation [J]. Journal of Computer Applications, 2014, 34(S1):341-344.)
[8]阎世梁,王银玲,张华.基于改进互补滤波器的低成本微小飞行器姿态估计方法[J]. 计算机应用,2013,33(7):2078-2082.(YAN S L, WANG Y L, ZHANG H. Improved complementary filter for attitude estimation of micro air vehicles using lowcost inertial measurement units [J]. Journal of Computer Applications,2013, 33(7):2078-2082.)
[9]BACHMANN E R, DUMAN I, USTA U Y, et al. Orientation tracking for humans and robots using inertial sensors[C]// Proceedings of the 1999 IEEE International Symposium on Computational Intelligence in Robotics and Automation. Piscataway, NJ: IEEE, 1999: 187-194.
[10]MADGWICK S O H, HARRISON A J L, VAIDYANATHAN R. Estimation of IMU and MARG orientation using a gradient descent algorithm[C]// Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics. Piscataway, NJ: IEEE, 2011: 1-7.
[11]MARINS J L, YUN X, BACHMANN E R, et al. An extended Kalman filter for quaternionbased orientation estimation using MARG sensors[C]// Proceedings of the 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, NJ: IEEE, 2001, 4: 2003-2011.
[12]张甜, 吴美平, 张开东, 等. 基于精密单点定位的航空重力仪运动加速度估计[J]. 导航与控制, 2014, 13(4):26-31.(ZHANG T, WU M P, ZHANG K D, et al. Airborne gravitometer kinematic acceleration determination based on precise point positioning[J].Navigation and Control, 2014, 13(4): 26-31.)
[13]李海涛. 加速度计/磁强计捷联惯导系统姿态解算方法研究[D].太原:中北大学,2007.(LI H T. Study on attitude algorithms of accelerometers/magnetometers strapdown inertial navigation system[D].Taiyuan: North University of China, 2007.)
[14]HENDERSON D M. Euler angles, quaternions, and transformation matrices[R]. Washington, DC:NASA JSC, 1977.

