基于多字典学习和图像块映射的超分辨率重建

莫建文 曾儿孟 张彤 袁华

摘要：针对单一冗余字典在稀疏表示图像超分辨率重建结果出现不清晰、伪影以及重建过程编码效率不高、运算时间过长的问题，提出一种基于多字典学习和图像块映射的超分辨率重建方法。该方法在传统稀疏表示的框架下，首先探索局部图像块的梯度结构信息，按梯度角度将训练样本块分类； 然后为每个子类样本集学习高低分辨率字典对，再结合最近邻思想应用生成的字典，为每个子类计算从低分辨率块到高分辨率块映射的函数；最后将重建过程简化为输入块和映射函数的乘积，在保证提高重建质量的同时减少了图像重建的时间。实验结果表明，所提算法在视觉效果有较大的提升，同时与锚点邻域回归算法相比，评价参数峰值信噪比（PSNR）平均提高约0.4dB。

关键词：稀疏表示；图像块分类；多字典学习；映射函数；邻域嵌入

中图分类号：TP391 文献标志码：A

Abstract：To overcome the disadvantages of the unclear results and time consuming in the sparse representation of image superresolution reconstruction with single redundant dictionary， a single image superresolution reconstruction method based on multidictionary learning and image patches mapping was proposed. In the framework of the traditional sparse representation， firstly the gradient structure information of local image patches was explored， and a large number of training image patches were clustered into several groups by their gradient angles， from those clustered patches the corresponding dictionary pairs were learned. And then the mapping function was computed from low resolution patch to high resolution patch in each clustered group via learned dictionary pairs with the idea of neighbor embedding. Finally the reconstruction process was reduced to a projection of each input patch into the high resolution space by multiplying with the corresponding precomputed mapping function， which improved the images quality with less running time. The experimental results show that the proposed method improves the visual quality significantly， and increases the PSNR （Peak SignaltoNoise Ratio） at least 0.4dB compared with the anchored neighborhood regression algorithm.

Key words：sparse representation； image patches classification； multidictionary learning； mapping function； neighbor embedding

0 引言

在医学诊断、卫星遥感、视频监控等数字成像领域中，都需要图像有较高的分辨率来为人的研究工作提供帮助。但是由于电子成像设备、环境以及传感器制造成本制约等因素的影响，实际获得的图像分辨率难以满足实际的应用需求， 因此通过软件技术手段，将输入的单幅或多幅低分辨率（Low Resolution， LR）图像恢复出相同场景的高分辨率（High Resolution， HR）图像的方法叫图像超分辨率（Image SuperResolution， ISR）重建，该技术在公共安全等众多领域发挥着重要的作用[1]。

为了获得超分辨率图像，目前软件算法主要分为基于插值的方法[2]、基于重建的方法[3]和基于学习的方法[4-8]三类。而近年来，随着机器学习和深度学习研究的深入，基于学习的重建算法取得了较大的进步[1，4-7]。Chang等[9]受流型学习算法启发，提出局部线性嵌入（Local Linear Embedding， LLE）的超分辨率重建方法，学习到高、低分辨率图像块之间的局部特征映射模型，通过最近邻域线性组合重建出高分辨率图像。Yang等[5-6]利用稀疏编码进行超分辨率重构，该方法首先假设高低分辨率图像块在过完备字典下有相同的稀疏系数，通过样本图像库训练高低分辨率字典对；然后求解待重建LR块在低分辨率字典下的稀疏系数，再结合高分辨率字典重建对应的HR块，从而得到最后的高分辨率图像。Zeyde等[7]在Yang的基础上把K次奇异值分解算法（Kmeans Singular Value Decomposition， KSVD）算法[9]应用到字典学习中，并用正交匹配追踪（Orthogonal Matching Pursuit， OMP）算法[10]对图像块稀疏编码，在速度和重建结果上都比Yang的有一定的提高。Dong等 [11]研究图像的非局部冗余结构，提出稀疏表示框架下非局部自回归模型，该模型学习Kmean聚类下的主成分分析（Principal Component Analysis， PCA）多字典，并引入回归模型和非局部约束，取得不错的效果。此外，Timofte等[4]提出一种快速的锚点邻域回归（Anchored Neighborhood Regression， ANR）算法，该算法结合稀疏编码和最近邻域嵌入（Neighbor Embedding， NE）思想，通过线下预先生成的映射关系，把超分辨率（SuperResolution， SR）过程简化为输入的LR块和映射矩阵相乘，在保证重建质量的同时极大提高SR速度。

虽然以上方法取得了不错的重建效果，但是它们建立的高度单一冗余字典对在稀疏分解中具有潜在的不稳定性，易产生视觉伪影[12]，且编码效率不高。针对这一不足，本文在Timofte的基础上提出了基于多字典学习和图像块映射（Multi Dictionary Learning and Image Patches Mapping， MDLIPM）的超分辨重建方法。MDLIPM方法在保持原有稀疏编码的本质基础上，通过图像局部梯度特征对图像块分类； 然后以KSVD算法对每个聚类库训练出高低分辨率字典对； 再结合最近邻域思想，利用训练到的字典对，学习从LR块到HR块的映射算子；最后将得到的映射函数应用到重建阶段，避免重建过程需要对每个图像块稀疏编码的开销，减少重建时间并提高重建质量。实验结果显示，本文方法的重建结果在主观视觉效果和客观评价参数上都取得不错的成绩，重建时间有一定的降低。

2 MDLIPM的超分辨方法

本文汲取邻域嵌入和稀疏表示重建的优点，提出的多字典学习和图像块映射超分辨率（Multi Dictionary Learning and Image Patches Mapping SuperResolution，MDLIPM SR）算法分为两个阶段：训练阶段，首先分析图像块的梯度结构，以此把训练库分成多个类，并为每个子类训练高低分辨率字典对{D（i）l，D（i）h}，i=1，2，…，K，然后利用字典对结合最近邻域回归思想，把邻域的搜索空间限制在字典空间内，以此为每个子类学习到从LR块到HR块的映射回归矩阵{f（i）}，i=1，2…，K；重建阶段，通过梯度信息判断LR块的所属子类后，把该子类的映射函数矩阵与LR块相乘直接重建出该LR块对应的HR图像块，避免了对图像块迭代求解稀疏系数的过程，从而减低重建时间并进一步得到重建的HR图像。

以上过程是Zeyde的两步字典训练思想[12]，因其字典训练速度快、编码算法效率高，故本文同样采用该思想进行字典学习。但由于其训练的单一字典不足以最稀疏表示具有某种特定结构特性的图像块，所以本文引进2.1节描述的基于梯度信息进行图像块分类，进而学习到每个类的字典，并以训练得到的多字典作为学习图像块映射函数的依据。

2.3 图像映射函数学习

本文引进Timofte等[4]的方法，把基于字典的SR方法和最近邻域方法相结合，限制邻域搜索空间在字典空间内，学习从LR块到HR块的映射函数，以避免在重建阶段对图像块稀疏编码的过程，保证重建质量的同时降低重建的时间。

正如式（5）所示，由于计算上的需要，基于邻域嵌入或稀疏表示的最小二乘问题都应用1范数正则项对权重系数或者稀疏系数加以限制。为了获得系数的解析解，本文重新调整正则约束项，把1范数约束改为2范数约束；然后以岭回归[15]求解办法获得系数的解析形式。调整过之后，NE系数问题表示为：

3 实验仿真与结果分析

为了验证MDLIMP算法的有效性，在训练阶段，本文选择包括人物、植物、建筑等69幅图像并分块，每个块的大小与学习单一字典的（Sparse coding Super Resolution，ScSR）、ANR的相同，设置为5×5，建立10000个高低分辨率图像块一一对应的训练集，并按照文中的梯度信息分类方法对样本集分成K=8类；然后以文中2.2节所述为每个子类学习原子数为512的高低分辨率字典对和映射回归矩阵，实验中映射回归学习式（18）的因子λ设为0.01。另外选取如图1所示的10幅标准测试图像，并通过双三次插值方法降采用的到待重建的LR图。整个测试实验平台为Inter Core i53230M CPU 2.60GHz，Matlab的版本为R2010b。

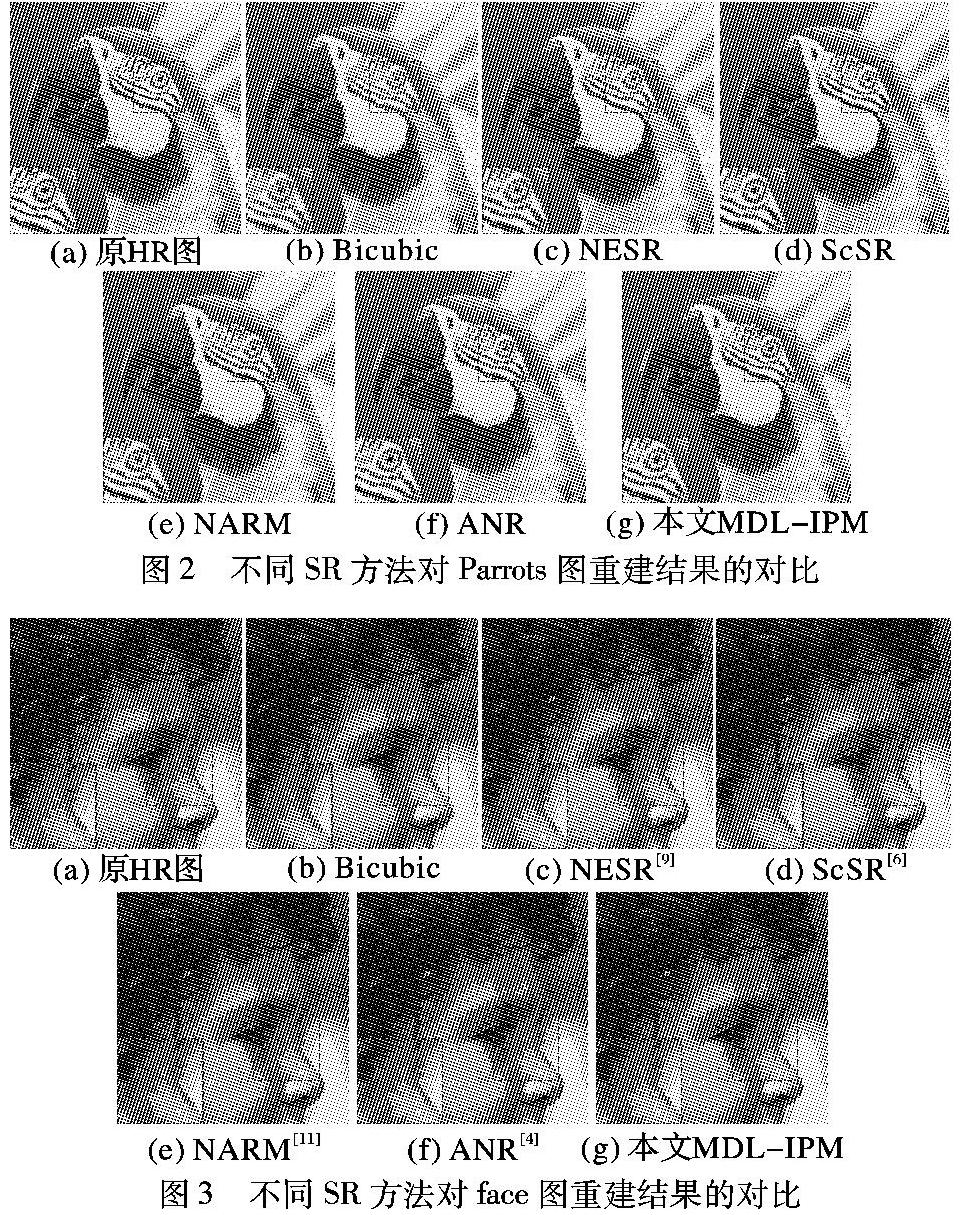
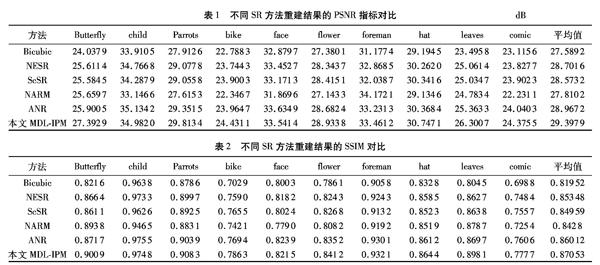
实验中以双三次插值算法Bicubic作为基准对比算法，并选择最近邻域局部线性嵌入方法（Neighbor Embedding Super Resolution，NESR）[9]、学习单一字典的ScSR算法[6]、Kmean聚类多字典的（Nonlocal Autoregressive Modeling，NARM）算法[11]和锚点邻域回归的（ANR）算法[4]作为对比实验，以检验本文方法的性能。待重建的LR图像放大因子s设为3，各方法重建结果的视觉主观对比如图2、3所示。客观评价参数峰值信噪比（Peak SignaltoNoise Ratio， PSNR）和结构相似度（Structural SIMilarity，SSIM）的对比结果见表1和表2。

图2比较了Parrots图在不同SR方法的重建结果，考察鹦鹉眼角周围的羽毛纹理细节部分。从视觉观测上来看，Bicubic基于平滑假设，故重建细节不明显，整体表明较为平滑；NESR算法丢失较多的高频信息，在恢复了部分细节的同时引入了不可估计的噪声，羽毛纹理出现锯齿、模糊等现象；而其他几个算法重建效果都比NESR的要好，重建出来的细节信息比NESR的要多，但仍有一些不足的地方。其中ScSR方法的细节重建明显同时仍出现振铃状；NARM算法在鹦鹉羽毛的边缘部分出现平滑和伪影效果，细节部分也不够清晰；ANR算法中鹦鹉眼角的纹理相对较好，但同样出现部分虚假信息。而本文MDLIPM方法在羽毛边缘的锐度和清晰度都得到明显的改善，重建的高频信息丰富，视觉效果更好。同样从图3 face图像人脸鼻子部分的雀斑看出，本文MDLIPM方法恢复的局部细节信息清晰、细腻，整体效果与原始图像更接近。从客观评价参数来看，从表1、2中可知，本文MDLIPM方法和NESR算法、ScSR算法以及NARM算法相比、在PSNR和SSIM上略有提高，其中单幅图像PSNR提高最多的有0.8dB左右，而平均也可提高大概0.4dB，说明本文方法确实可行有效。同时，添加局部对比度的质量评价方法（Quality Index based on Local Variance， QILV）[16]、模糊系数K[17]和质量因素Q[18]，对重建结果进行比较，其中各方法重建质量评估参数平均值如表3所示。从表中可以看出，本文方法均取得较好的成果。

另外在重建时间上，不考虑训练时间，本文仅仅对各个方法的重建时间作比较。NESR算法需要对每个待重建块搜索最近邻域，故重建时间是最长的。从表4看出，ScSR、NARM、ANR算法以及本文方法平均的重建时间分别为42.46s、189.97s、0.45s和2.91s。由于本文方法在重建时，需要判断待图像块所属类别，导致时间比ANR算法略长，但显著提高了重建图像的质量。

4 结语

本文提出了基于多字典和图像块映射的超分辨率重建方法，该方法探索局部图像块的梯度结构信息，并依据局部块的梯度方向对训练样本块分类，再应用两步字典训练方法为每个分类样本训练高低分辨率字典对；同时引入了最近邻域回归思想，在每个类中从学习到的字典对中建立从低分辨率块到高分辨率块的映射矩阵。在重建过程，首先对每个待重建块归并到所属类中，然后应用该类映射矩阵重建相对应的高分辨率图像块，避免了对每个图像块稀疏编码的运算开销。实验结果显示，在保留经典稀疏编码图像超分辨率重建效果的同时，一定程度上提高SR重建效率、降低重建时间。未来的研究工作将寻求更好的优化方法，进一步提高重建质量，以及应用分布式并行处理降低训练阶段的时间；同时将进一步讨论参数设置，如图像块的大小、样本集聚类数K等对重建效果的影响。

参考文献：

[1]CHEN X， QI C. Nonlinear neighbor embedding for single image superresolution via kernel mapping[J]. Signal Processing， 2014， 94（1）： 6-22.

[2]LIU X， ZHAO D， ZHOU J， et al. Image interpolation via graphbased Bayesian label propagation[J]. IEEE Transactions on Image Processing， 2014， 23（3）： 1084-1096.

[3]RASTI P， DEMIREL H， ANBARJAFARI G. Image resolution enhancement by using interpolation followed by iterative back projection[C]// Proceedings of the 21st IEEE on Signal Processing and Communications Applications Conference. Piscataway， NJ： IEEE， 2013： 1-4.

[4]TIMOFTE R， DE V， VAN GOOL L. Anchored neighborhood regression for fast examplebased superresolution[C]// Proceedings of the 2013 IEEE International Conference on Computer Vision. Piscataway， NJ： IEEE， 2013： 1920-1927.

[5]YANG J， WRIGHT J， HUANG T S， et al. Image superresolution via sparse representation[J]. IEEE Transactions on Image Processing， 2010， 19（11）： 2861-2873.

[6]YANG J， WRIGHT J， HUANG T， et al. Image superresolution as sparse representation of raw image patches[C]// Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE，2008： 1-8.

[7]ZEYDE R， ELAD M， PROTTER M. On single image scaleup using sparserepresentations[C]// Proceedings of the 7th International Conference on Curves and Surfaces. Heidelberg： Springer， 2012： 711-730.

[8]AHARON M， ELAD M， BRUCKSTEIN A. The KSVD： an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing， 2006， 54（11）： 4311-4322.

[9]CHANG H， YEUNG D Y， XIONG Y. Superresolution through neighbor embedding[C]// Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE， 2004， 1： 275-282.

[10]RUBINSTEIN R， ZIBULEVSKY M， ELAD M. Efficient implementation of the KSVD algorithm using batch orthogonal matching pursuit[R/OL].[2015-11-04].https：//www.researchgate.net/publication/251229200.

[11]DONG W， ZHANG L， LUKAC R， et al. Sparse representation based image interpolation with nonlocal autoregressive modeling[J]. IEEE Transactions on Image Processing， 2013， 22（4）： 1382-1394.

[12]ELAD M， YAVNEH I. A plurality of sparse representations is better than the sparsest one alone[J]. IEEE Transactions on Information Theory， 2009， 55（10）： 4701-4714.

[13]FENG X G， MILANFAR P. Multiscale principal components analysis for image local orientation estimation[C]// Proceedings of IEEE Conference Record of the 36th Asilomar Conference on Signals， Systems and Computers. Piscataway， NJ： IEEE，2002， 1： 478-482.

[14]YANG S， WANG M， CHEN Y， et al. Singleimage superresolution reconstruction via learned geometric dictionaries and clustered sparse coding[J]. IEEE Transactions on Image Processing， 2012， 21（9）： 4016-4020.

[15]TIKHONOV A N， ARSENIN V I A. Solutions of illposed problems[J]. Mathematics of Computation， 1978， 32（144）：491.

[16]AJAFERNANDEZ S， SANJOSESTPAR R， ALBEROLALOPEZ C， et al. Image quality assessment based on local variance[C]// Proceedings of the 28th Annual IEEE International Conference on Engineering in Medicine and Biology Society. Piscataway， NJ： IEEE，2006： 4815-4818.

[17]黄文辉， 陈仁雷， 张家谋. 数字视频图像质量客观测量方法的改进与实现[J]. 北京邮电大学学报， 2005， 28（4）： 87-90. （HUANG W H，CHEN R L， ZHANG J M. Improvement and implementation of objective digital video quality measurement[J].Journal of Beijing University of Posts and Telecommunications，2005， 28（4）： 87-90.）

[18]WANG Z， SHEIKH H R， BOVIK ALAN C. Objective Video Quality Assessment[M]. Boca Raton： CRC Press， 2003：214-220.