基于食物链机制的动态多物种粒子群算法

刘角 马迪 马腾波 张玮

摘要：针对粒子群优化（PSO）算法在解决多峰函数时容易陷入局部最优的问题，提出了一种基于食物链机制的动态多物种粒子群（DSPSO）算法。受生物界的启发，引入食物链机制来保证种群的多样性，并结合繁殖机制使得算法具有良好的优化性能。食物链机制中，整个标榜群被分为几个子种群，每个子种群都能够捕食另外一个子种群。通过一定概率发生的捕食现象使得标榜群得以进化，剔除对种群贡献小的粒子，并通过繁殖策略生成新的粒子。种群通过不断地进化保证了种群的多样性，同时通过剔除较差粒子的误导作用使算法的进化更有效率。为了验证算法的有效性，选择了包括偏移函数、旋转函数在内的10个测试函数来测试DSPSO算法的性能。实验结果表明DSPSO算法有着良好的寻优性能。与PSO、局部版本的粒子群（LPSO）算法、动态多群粒子群（DMSPSO）算法和全面学习粒子群（CLPSO）算法相比，DSPSO算法不仅能够得到较高精度的解，而且还具有较高的可信度。

关键词：粒子群优化算法； 食物链机制；动态多物种

中图分类号：TP301.6 文献标志码：A

Abstract：a novel Dynamic multiSpecies Particle Swarm Optimization （DSPSO） algorithm based on food chain mechanism was proposed aiming at the problem that the basic Particle Swarm Optimization （PSO） algorithm is easy fall into local optimal solution when solving multimodal problems. Inspired by the natural ecosystem， a food chain mechanism and a reproduction mechanism were employed to keep the swarm diversity and good performance. In food chain mechanism， the swarm was divided into several subswarms， and each subswarm could prey on the others. The memory leader swarm was evolved and the less contributed particle was eliminated through predation， and then the new particle was generated through reproduction mechanism. The diversity was kept through the evaluation of the swarm， and the efficiency of the algorithm was enhanced through eliminating the misleading effect of the less contributed particles. In order to verify the effectiveness of the algorithm， ten benchmark problems including shifted problems and rotated problems were chose to test the performance of DSPSO. The experimental results show that DSPSO has a well optimizing performance. Compared with PSO algorithm， Local version Particle Swarm Optimization （LPSO） algorithm， Dynamic MultiSwarm Particle Swarm Optimization （DMSPSO） algorithm and Comprehensive Learning Particle Swarm Optimization （CLPSO） algorithm， DSPSO algorithm not only obtains more accurate solutions， but also has higher reliability.

Key words：Particle Swarm Optimization （PSO） algorithm； food chain mechanism； dynamic multispecies

0 引言

粒子群优化（Particle Swarm Optimization，PSO）算法是Kennedy等[1]于1995年提出的一种群智能优化算法，其思想来源于鸟群的捕食行为。由于其寻优速度快，易于实现，相较与其他元启发式优化算法具有良好的性能，其出现以后便迅速得到了国际学者的关注并广泛应用于诸如神经网络、资源调度、图像处理、电容配置等诸多领域。

尽管粒子群算法有着诸多优点，但是和其他元启发式算法一样，它也有着容易陷入局部最优、寻优后期收敛速度慢等缺点。为了克服这些缺点，许多学者都试图从各个角度来提升粒子群算法的性能[2-3]。算法的改进总体分为三类，分别为：参数选取机制、种群拓扑结构以及学习机制。在参数选取方面，Shi等[4]提出惯性权重线性递减的粒子群算法，该算法前期具有较好的探索能力，后期具有较强的勘探能力，从而兼具良好的全局搜索能力和局部搜索能力；Zhan等[5]提出了一种自适应粒子群算法，能够根据不同的情况自动调整算法的加速因子和惯性权重。在种群拓扑结构方面，Kennedy等[6]研究了不同拓扑结构下粒子群算法的性能，一些典型的拓扑结构，如环形拓扑、冯诺依曼拓扑被应用到粒子群算法中。其中，采用环形拓扑的粒子群算法被称为局部版本的粒子群（Local version Particle Swarm Optimization，LPSO）算法；Mendes等[7]提出了一种新的改进粒子群算法叫作全信息粒子群算法（Fully Informed Particle Swarm，FIPS）。FIPS认为没有必要只选用全局最优点和局部最优点引导算法进化，所有的个体最优点均可以作为算法的进化目标，即每个粒子都可以依据其他粒子包含的信息进行进化。Liang等[8]提出了一种动态多群粒子群算法（Dynamic MultiSwarm Particle Swarm Optimization，DMSPSO），种群具有动态变化的拓扑结构，这种结构使得算法的信息在种群中的传播速度降低，避免粒子过快聚集，从而提高了粒子群算法的寻优性能。在学习机制方面，一些改进算法借助于其他元启发式算法的思想改善了粒子群算法的性能，例如Beheshti[9]提出的万有引力粒子群算法，Lim等[10]提出的教学与同伴学习粒子群算法。还有一些具有新颖的学习机制，例如Zhan等[11]提出的正交学习粒子群算法，Liang等[12]提出的全面学习粒子群算法（Comprehensive Learning Particle Swarm Optimization，CLPSO），Ren等[13]提出的分散学习粒子群算法，这些算法均明显地提升了粒子群算法的性能。

然而，早熟收敛仍然是粒子群算法的一大缺点，而多样性的丧失是导致粒子群算法陷入早熟收敛的一个重要原因。为了防止多样性的丧失，并使得算法更有效地进化，本文提出一种基于食物链机制的动态多物种粒子群算法（Dynamic multiSpecies Particle Swarm Optimization， DSPSO）。该算法受生物界的启发，提出通过食物链机制来保证种群的多样性，结合繁殖机制使得算法具有良好的优化性能，很大程度上改善了粒子群算法容易陷入局部收敛的缺点，并且提升了粒子群算法的收敛效率。

2 基于食物链机制的动态多物种粒子群算法

传统的粒子群算法有着容易陷入局部收敛的缺点，在解决多峰问题时并不能得到良好的最优解。为了克服其缺点，本文提出了基于食物链机制的改进粒子群算法（DSPSO）。DSPSO引入了两种机制，分别为食物链机制和繁殖机制，本章将对这两种机制的构架及目的进行详细的说明。

2.1 食物链机制

传统的粒子群算法中，整个种群均以个体最优点和群体最优点为标榜进行进化，尽管这样的处理能够使算法拥有较快的收敛速度，但同时有可能使种群的多样性快速流失，导致算法陷入局部收敛。另一方面，作为种群标榜的被记录的个体最优点，也就是标榜群pbest中，有很多较差的个体最优点并不能够为整个种群的进化作出贡献，这些被记录的个体最优点则需要被排除。由以上两点可以看出，粒子群算法的性能很大程度上取决于标榜的选择方式。因此，不仅仅是粒子群需要进化，标榜群也需要按照一定的规律进化并选取。

众所周知，生物界能够很好地保持物种的多样性，其中最有特色的就是食物链。食物链的存在使得能量在生态系统中互相传导，并且保证了各个物种在生物界的平衡。食物链机制通过模仿生物界的这种特点，对标榜群进行进化。在食物链机制中，整个标榜群被分为几个子种群，每个子种群都能够捕食另外一个子种群，但同时也会被第三个子种群捕食。在本文算法中，各个子种群的捕食结构为环形。在算法进化的每一代中，都会依次判断各个子种群是否发生捕食现象，一旦发生捕食现象，当前子种群的最差粒子则被捕食，此时该粒子将被剔除，取而代之的则是捕食者所在子种群按繁殖机制所繁殖的标榜粒子，该标榜粒子则被划入到捕食者所在种群。捕食是否发生则取决于捕食概率P，而P根据一定规则进行计算，该规则受生物界捕食规律启发。对于每个子种群，若捕食者子种群适应度值大于被捕食者子种群适应度值，则代表捕食者子种群所在环境适合生存，当前被捕食者种群则更容易被捕食。捕食概率计算方案如下：

2.2 繁殖策略

繁殖是一种常见的自然现象，也是物种进化的关键很多算法，如差分进化算法、遗传算法，都曾模仿过这种现象。在文献[11]中，Liang等认为，对于一些已知的个体最优点，可能对于某些维所得位置已经非常接近全局最优点，但是由于其他维数得到的结果比较差而造成了整个的最优点有较差的适应度值，因此，本文模仿Liang等的全面学习机制构造了一种繁殖机制，其公式表现为：

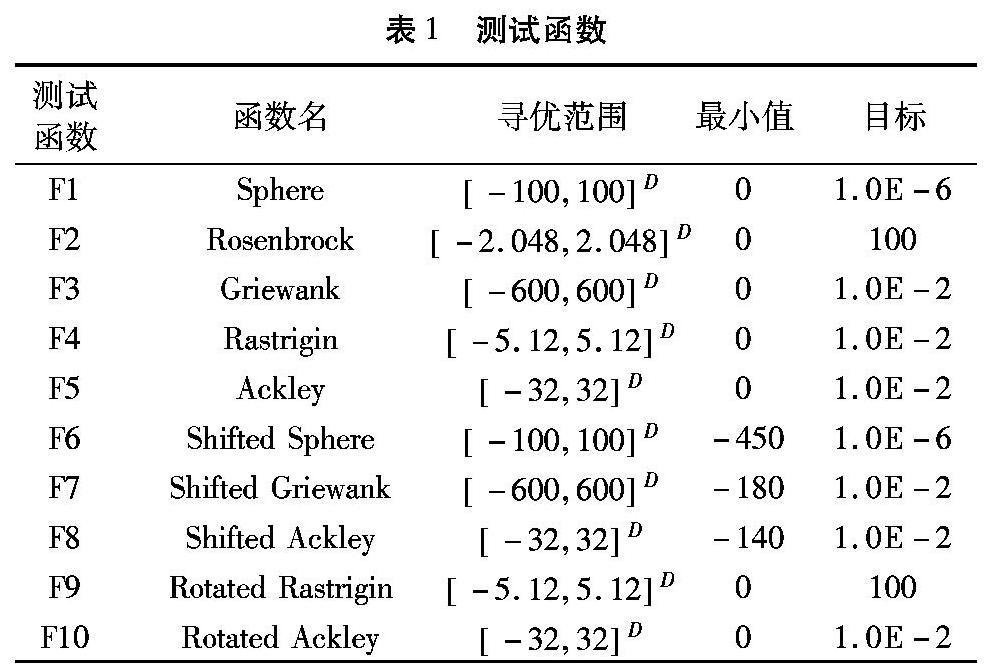
在实验对比仿真中，种群规模均设置为50，测试函数的维数均为30维，速度上限被设置为寻优范围的0.1倍，DSPSO的子种群数量设置为5。每组实验算法独立计算25次，单个实验中，算法在经过3.00E+5次函数计算次数后停止计算。需要注意的是，惯性权重在2.00E+5函数计算次数之前保持线性递减，当函数计算次数大于2.00E+5后，惯性权重将保持0.4不变。各个算法的具体参数设置如表2所示。

需要注意的是，PSO、LPSO和DMSPSO的加速因子c1和c2分别被设置为2和1，与传统的设置方法略有不同。对于CLPSO和DSPSO，如表2的设置方式使得算法具有良好的性能，如若令加速因子为2，算法的性能不佳。之所以在相同的参数下几种算法的性能差异较大，是因为PSO、LPSO和DMSPSO采用的最优点粒子是传统意义上的全局最优点和局部最优点，而CLPSO和DSPSO采用的则分别是全面学习机制遴选组合出的全面学习标榜粒子和食物链机制遴选出的标榜粒子，其算法本质决定了算法的社会学习因子并不能设置太高。因此对于CLPSO和DSPSO，其参数设置并没有按照传统的设置方法设置。为了使不同的算法具有可比性，本文同样将PSO、LPSO和DMSPSO的加速因子c1和c2设置为2和1。而对于CLPSO，本文则采用文献[12]中推荐的设置方法。

3.1 算法参数灵敏度分析

为了测试辅助最优点选择周期period和辅助最优点选择参数n对算法性能的影响，本文对参数period和n作灵敏度分析。首先将period和n分别设置为5、25，然后保持n为25不变，改变period。选出具有最好性能的period值之后保持period为最佳值不变，改变n值，最后得到最佳参数，其他参数设置如表2所示。实验中以F1、F4、F5调整算法参数，对于每个测试函数与参数组合，实验独立执行10次，结果为10次实验得到的最优适应度值的平均值，实验结果如表3和表4所示。从实验结果可以得知，当period和n分别为5和25时，算法具有良好性能。

3.2 算法性能分析

为了全面反映DSPSO的性能，本节选取了4种不同的改进粒子群算法作为对比来反映DSPSO的有效性。4种算法的参数设置、拓扑结构等见表2。仿真结果见表5、表6。表5中，平均精度代表算法在经过2.00E+5次函数计算后得到的适应度值与函数最优值偏差的均值，标准差代表2.00E+5次函数计算后得到的适应度值的标准差，最优值则为经过2.00E+5次函数计算后得到的适应度值与函数最优值偏差的最小值；T检验值为将DSPSO于其他算法进行比较后的T检验值，目的是为了验证性能的提升是否有统计学意义；h则代表根据T检验值得到的DSPSO的性能是否得到了提升，以置信度95%为界，若提升则表示为“+”，具有相同的统计学意义则为“=”，否则为“-”。Rank代表各个算法的排名。表6列出了算法的成功率以及达到目标精度时的函数计算次数。

1）精度对比。

根据表5可以看出，DSPSO有着非常明显的优势。DSPSO拥有最高的平均排名，其值为1.9，而PSO，LPSO，DMSPSO和CLPSO的平均排名则分别为4.3、2.4、2.3和3.6，且对于大部分测试函数，DSPSO都优于其他四种改进算法。尤其是F2、F3、F6、F9，DSPSO得到的平均精度值都明显地优于其他算法，且根据h值可以看出其提升大多数都具有统计意义。

但是从实验结果中也可以看出，对于大多数测试函数，DSPSO并不能完全地优于其他四种改进算法，其Rank值多数都为2，但从算法获得的最优值来看，对于这些函数DSPSO都能够获得比较优异的结果。可见，食物链机制的引入使得算法能够保持良好的种群多样性，从而使得算法不容易陷入局部最优，得到的结果更加接近真实的最优值，因此拥有较好的寻优精度。

2）寻优效率对比。

根据表6中的计算次数值可以看出，DSPSO效率要低于PSO、LPSO和DMSPSO。PSO、LPSO、DMSPSO、CLPSO和DSPSO的平均计算次数分别为46282.58、56566.40、76263.11、118978.00和103180.32。对于选出的10个测试函数，DSPSO拥有较高的函数计算次数。但DSPSO的寻优效率要明显高于CLPSO。算法对函数F4、F6、F9的寻优过程的对比轨迹如图1～3所示。

由此可见，食物链机制使得算法的精度有所提升，但使算法的寻优效率变低。食物链机制使得算法消耗一部分计算在食物链机制的执行上，因此相较于PSO、LPSO和DMSPSO而言，算法的寻优效率相对较低。

3）寻优结果可信度。

PSO、LPSO、DMSPSO、CLPSO和DSPSO的平均成功率分别为70.00%、90.00%、89.60%、100.00%和94.40%。DSPSO得到的结果具有较高的可信度，在解决这10个测试函数时，其中的9个问题都以100%的概率达到了目标精度，仅仅在解决F4时没有达到100%。但是相对而言，CLPSO具有更好的可信度，对所有的寻优问题CLPSO均达到了100%的可信度。可见食物链机制能够很好地抑制算法发生早熟收敛现象，提升算法的可信度。

4） 算法时间复杂度分析。

标准粒子群算法的时间复杂度为TPSO（N）=O（NDT），其中N、D、T分别为粒子总数、搜索维数和最大迭代次数。由于DSPSO引入了食物链机制和繁殖策略，因此其时间复杂度应为TPSO（N）=O（NDT）+ O（NT）。表7为各算法经过3.00E+5次函数计算次数后所消耗的时间，由结果可知，相对于PSO、LPSO和DMSPSO， DSPSO消耗的计算时间较长，拥有较高的计算复杂度。相对而言，CLPSO拥有最高的计算复杂度。

总体而言，尽管DSPSO算法还有一些不足，但它还是拥有不错的性能，相对其他四种改进算法，DSPSO算法拥有非常优秀的精度和可信度。

4 结语

受生物界中的食物链机制启发，本文提出了一种具有食物链结构的改进粒子群算法DSPSO。与PSO算法、局部版本的粒子群（LPSO）算法、动态多群粒子群（DMSPSO）算法和全面学习粒子群（CLPSO）算法相比，DSPSO拥有更好的寻优能力，更容易避免陷入早熟收敛；其得到的解质量好、寻优效率高、可信度高，具有更好的优越性。但是，DSPSO仍然有一些不足之处，它并不能完全超越其他改进粒子群算法，在解决多峰函数时并不能够保证每次都能得到高质量的解，且计算复杂度相对较高。在以后的研究中，我们将就这些问题对DSPSO进行进一步改进，提升该算法的性能。

参考文献：

[1]KENNDY J， EBERHART R. Particle swarm optimization[C]// Proceedings of the 4th IEEE International Conference on Neural Networks. Piscataway， NJ： IEEE， 1995： 1942-1948.

[2]饶兴华， 王文格， 胡旭. 多样性反馈与控制的粒子群优化算法[J]. 计算机应用， 2014， 34（2）：506-509.（RAO X H， WANG W G， HU X. Diversity feedback and control particle swarm optimization algorithm[J]. Journal of Computer Applications， 2014， 34（2）：506-509.）

[3]吕莉， 赵嘉， 孙辉. 具有反向学习和自适应逃逸功能的粒子群优化算法[J]. 计算机应用， 2015， 35（5）：1336-1341.（LYU L， ZHAO J， SUN H. Partical swarm optimization algorithm using oppositionbased learning and adaptive escape[J]. Journal of Computer Applications， 2015， 35（5）：1336-1341.）

[4]SHI Y， EBERHART R. A modified particle swarm optimizer[C]// Proceedings of the 1998 IEEE World Congress on Computational Intelligence. Piscataway， NJ： IEEE， 1998：69-73.

[5]ZHAN ZH， ZHANG J， LI Y， et al. Adaptive particle swarm optimization[J]. IEEE Transactions on Systems， Man， and Cybernetics， 2009， 39（6）： 1362-81.

[6]KENNEDY J， MENDES R. Population structure and particle swarm performance[C]// Proceedings of the 2002 Congress on Evolutionary Computation. Piscataway， NJ： IEEE， 2002：1671-1676.

[7]MENDES R， KENNEDY J， NEVES J. The fully informed particle swarm： simpler， maybe better[J]. IEEE Transactions on Evolutionary Computation， 2004， 8（3）： 204-210.

[8]LIANG J， SUGANTHAN P N. Dynamic multiswarm particle swarm optimizer[C]// Proceedings of the 2005 IEEE Swarm Intelligence Symposium. Piscataway， NJ： IEEE， 2005：124-129.

[9]BEHESHTI Z， SHAMSUDDIN S M H. CAPSO： Centripetal accelerated particle swarm optimization[J]. Information Sciences， 2014， 258：54-79.

[10]LIM W H， MATISA N A. Teaching and peerlearning particle swarm optimization[J]. Applied Soft Computing， 2014， 18（18）：39-58.

[11]ZHAN ZH， ZHANG J， LI Y， et al. Orthogonal learning particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation， 2011， 15（6）： 832-847.

[12]LIANG J J， QIN A K， SUGANTHAN P N， et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions [J]. IEEE Transactions on Evolutionary Computation， 2006， 10（3）： 281-295.

[13]REN Z， ZHANG A， WEN C， et al. A scatter learning particle swarm optimization algorithm for multimodal problems [J]. IEEE Transactions on Cybernetics， 2014， 44（7）： 1127-1140.

[14]SUGANTHAN P N， HANSEN N， LIANG J J， et al. Problem definitions and evaluation criteria for the CEC 2005 special session on realparameter optimization[R]. Singapore： Nanyang Technological University， 2005.