改进的基于粒子群优化的支持向量机特征选择和参数联合优化算法
张进 丁胜 李波


摘要:针对支持向量机(SVM)中特征选择和参数优化对分类精度有较大影响,提出了一种改进的基于粒子群优化(PSO)的SVM特征选择和参数联合优化算法(GPSOSVM),使算法在提高分类精度的同时选取尽可能少的特征数目。为了解决传统粒子群算法在进行优化时易出现陷入局部最优和早熟的问题,该算法在PSO中引入遗传算法(GA)中的交叉变异算子,使粒子在每次迭代更新后进行交叉变异操作来避免这一问题。该算法通过粒子之间的不相关性指数来决定粒子之间的交叉配对,由粒子适应度值的大小决定其变异概率的大小,由此产生新的粒子进入到群体中。这样使得粒子跳出当前搜索到的局部最优位置,提高了群体的多样性,在全局范围内寻找更优值。在不同数据集上进行实验,与基于PSO和GA的特征选择和SVM参数联合优化算法相比,GPSOSVM的分类精度平均提高了2%~3%,选择的特征数目减少了3%~15%。实验结果表明,所提算法的特征选择和参数优化效果更好。
关键词:支持向量机;特征选择;参数优化;粒子群优化算法;遗传算法;不相关性指数
中图分类号:TP301.6 文献标志码:A
Abstract:In view of feature selection and parameter optimization in Support Vector Machine (SVM) have great impact on the classification accuracy, an improved algorithm based on Particle Swarm Optimization (PSO) for SVM feature selection and parameter optimization (GPSOSVM) was proposed to improve the classification accuracy and select the number of features as little as possible. In order to solve the problem that the traditional particle swarm algorithm was easy to fall into local optimum and premature maturation, the crossover and mutation operator were introduced from Genetic Algorithm (GA) that allows the particle to carry out cross and mutation operations after iteration and update to avoid the problem in PSO. The cross matching between particles was determined by the noncorrelation index between particles and the mutation probability was determined by the fitness value, thereby new particles was generated into the group. By this way, the particles jump out of the previous search to the optimal position to improve the diversity of the population and to find a better value. Experiments were carried out on different data sets, compared with the feature selection and SVM parameters optimization algorithm based on PSO and GA, the accuracy of GPSOSVM is improved by an average of 2% to 3%, and the number of selected features is reduced by 3% to 15%. The experimental result show that the features selection and parameter optimization of the proposed algorithm are better.
Key words:Support Vector Machine (SVM); feature selection; parameter optimization; Particle Swarm Optimization (PSO) algorithm; Genetic Algorithm (GA); no correlation index
0 引言
支持向量机(Support Vector Machine,SVM)用于高维数据分类具有较好的分类性能。由于高维数据中不可避免地存在与其他特征相冗余的特征,不仅降低SVM分类精度,而且增加算法的时间和空间复杂度。通过特征选择算法实行降维[1-4]能有效消除冗余特征,提高算法性能。此外,在SVM分类问题中,参数设置对分类器的性能有较大的影响,合适的参数能提高分类器的性能。SVM的参数选择问题,其实质就是一个优化问题。现有参数优化的方法中,交叉验证[5]是目前应用较为普遍的一种方法,该方法易于实现,但是计算量大,尤其对于大样本问题。近几年来,进化计算算法成为参数优化的新型优化算法,文献[6]提出了基于蚁群算法的支持向量机参数选取算法;文献[7]提出了采用遗传算法优化最小二乘支持向量机参数的方法。上述算法仅对特征子集或对SVM参数单独进行优化。实际上,特征选择与参数优化在提高SVM分类精度上相互影响。如何将两者联合优化以获得最优分类性能,是目前SVM分类问题研究领域的一个热点。文献[8]提出了基于蜜蜂算法的SVM特征选择和参数优化,文献[9]提出了应用遗传算法(Genetic Algorithm,GA)同步进行特征选择和参数优化的方法(GASVM)。其中,遗传算法是一种全局优化算法,虽然克服了一般迭代方法中容易陷入局部最优的缺点,但是搜索速度较慢。粒子群优化 (Particle Swarm Optimization,PSO) 算法是一种新兴的优化算法,近年来在许多领域得到应用,如用粒子群算法用于图像处理[10]、优化问题[11]和分类问题[12]。近年来,出现基于PSO的特征选择和参数同步优化的(PSOSVM)算法[13]。PSO算法虽然搜索速度较快,但是存在容易陷入局部最优和早熟的问题。针对这一情况,可以将遗传算法和粒子群算法结合起来,用于特征选择和SVM参数同步优化。
本文将GA的交叉和变异机制引入到PSO中,提出了一种改进的基于PSO的SVM特征选择和参数联合优化算法(GPSOSVM)。
2 GPSOSVM算法
传统粒子群优化算法对于位置与速度的更新具有很好的导向性,对空间最优解的逼近能力较强,但是存在容易陷入局部最优解、搜索精度较低、后期迭代效率不高等缺点。而遗传算法(GA)的交叉和变异操作,都缺乏明确的导向性,对空间最优解的逼近能力不足,但是能扩大搜索空间,对空间最优解的搜索能力相对较强,不容易陷入局部最优。本文把两种算法进行结合,将遗传算法的交叉和变异机制引入到粒子群优化算法中,提出了GPSOSVM算法,在粒子每次迭代更新后通过交叉和变异操作产生出新的个体,对当前适应度较低的个体进行替换,拓展粒子群在迭代中不断缩小的搜索空间,使粒子跳出当前搜索到的局部最优值位置,在更大的空间搜索,寻找更优值。
2.1 粒子编译码
2.3 惯性权重
惯性权重w是粒子保持原来速度的系数,体现的是继承当前速度的程度,较大的值利于全局搜索,而较小的值利于局部搜索。一般情况下,w设为1。为了更好地平衡算法的全局搜索与局部搜索能力,采用动态惯性权重,在迭代初期设置较大的惯性权重搜索较大的区域,而迭代后期设置较小的惯性权重进行更精细的局部搜索。和一般线性递减惯性权重的方式不同,本文采用一种惯性权重非线性递减方式,使惯性权重前期下降较慢,后期下降较快,进行更精确的搜索。惯性权重更新公式如下:
2.4.2 交叉方式
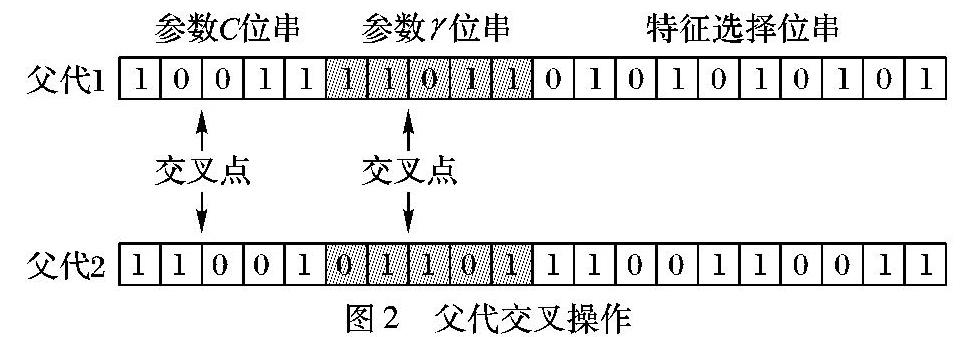
本文中粒子是由惩罚参数C、核参数γ和特征子集三段组成,在选择交叉点时,对三部分位串都进行交叉,保证交叉操作作用到三部分位串上。惩罚参数C和核参数γ位串采用单点交叉法,即在该位串上只选择一个交叉点。交叉点的位置决定了子代基因的组成方式,如果交叉点选取得不合适,则交叉后很可能产生和父代一样的个体,特别是在迭代后期由于粒子群中粒子逐渐趋于一致,每个粒子基因趋于相同,导致出现无效交叉操作的可能性更大。如下所例,由于交叉点位置选取得不合适导致出现和父代一样的子代。
2.6 算法流程
算法输入 数据集D,参数C的最大值Cmax和最小值Cmin,参数γ的最大值γmax和最小值γmin,适应度函数权重Wa和Wf,粒子长度num,粒子群数目group,最大迭代次数Dmax,学习因子c1和c2,初始惯性权重wstart,迭代至最大次数时的惯性权重wend。
算法输出 最优个体及其适应度值,优化的特征子集,支持向量的参数C、γ和对应的分类精度。
步骤1 对数据集D进行规范化处理,将全部特征值都变换到[0,1]区间上,并将数据集分为训练集D1和测试集D2。
步骤2 设定输入各参数,初始化粒子群X。
步骤3 把粒子的二进制码根据式(7)转换成支持向量机的参数C、γ和数据特征子集,利用SVM进行学习和训练,得出分类精度。最后由式(8)计算出粒子群中每个粒子的适应度值。
步骤4 根据粒子适应度,更新每个粒子个体历史最优位置Pbesti以及整个粒子群的群体历史最优位置Gbest。
步骤5 根据式(9)更新惯性权重w(k),再根据式(1)和(2)更新种群X的速度和位置,计算得出这一代粒子的适应度值。
步骤6 新建粒子群Y,令Y=X。
步骤7 根据本文提出的交叉操作方法(见2.4节),对种群Y进行交叉操作。
步骤8 根据本文提出的变异操作方法(见2.5节),对种群Y进行变异操作。
步骤9 对新种群Y求取适应度值,对比X和Y中对应个体的适应度值,对Y中适应度值比X高的个体对X进行替换,并更新X中的Pbesti和Gbest。
步骤10 判断是否达到最大迭代次数:若已经达到,则输出最优个体;如果没有达到,则跳转到步骤5继续运行。
步骤11 通过最优个体得到参数C、γ和特征子集,构造GPSOSVM分类器,得出最终的分类精度。
3 实验研究
3.1 实验环境和实验数据
算法用Matlab编程实现,计算机配置为双核,内存4GB,CPU速度为3.50GHz,SVM采用LIBSVM[15]。为验证算法的有效性,采用多个UCI数据集进行研究,如表1所示。
3.2 实验评价方法
为了验证算法的效果,实验采用K折交叉验证求取分类精度,以减小SVM分类的误差。把表1中每个数据集随机分成n个子集,每次取一个作为测试集,其余n-1个合并为训练集。每个子集分别做一次测试,连续运行n次,然后取n次实验结果的算术平均值作为运行一次所得到的分类精度。本实验中n值取10。
表2是GPSOSVM算法同SVM算法,PSOSVM算法和GASVM算法在相同数据集上所达到分类精度的比较。其结果是算法在某一数据集上连续运行10次所得出精度的平均值。表3是GPSOSVM算法同PSOSVM算法和GASVM算法在相同数据集上所选出的特征选择数目比较。其结果是算法在数据集上连续运行10次所得出的平均值。
3.5 实验分析
从图2看出,相比PSOSVM算法和GASVM算法,本文提出的GPSOSVM算法得到的最佳适应度值最高,能找到最优的个体,其参数优化和特征选择能力更强。GPSOSVM算法与另外两种算法对比,GASVM算法过早陷入了成熟,PSOSVM算法最佳适应度值相对不高,GPSOSVM算法在迭代过程中能找到适应度更高的个体。从图3可以看出,GPSOSVM算法迭代中的平均适应度值的震荡范围更大,也就是说在解空间中搜索范围更大,不易陷入局部最优解。
从表2看出,SVM算法的分类精度明显低于另外三种算法,可以证明进行特征选择和参数优化后的SVM分类器分类效果会更好。在三种优化算法中,GPSOSVM算法的分类精度同PSOSVM算法和GASVM算法相比更高。比如对于二分类数据集Sonar,GPSOSVM算法总命中率为88.7500%,PSOSVM算法总命中率为83.8462%,GASVM算法总命中率为84.5192%。GPSOSVM算法比PSOSVM算法提高4.9038个百分点,比GASVM算法提高4.2308个百分点。
对于多分类数据集Air,GPSOSVM算法比PSOSVM算法提高2.0612个百分点,比GASVM算法提高2.6741个百分点。此外,GPSOSVM算法同另外三种算法相比,得到的正命中率和反命中率相差最小,因此,均衡性更好。
由于SVM算法没有特征选择能力,故对其他三种算法所选出特征子集的数目进行比较。从表3可以看出,GPSOSVM算法同PSOSVM算法和GASVM算法相比,GPSOSVM算法所选出特征子集的数目要少于PSOSVM算法和GASVM算法所选的数目。以特征数目较多的数据集Sonar(特征数目为60)为例,GPSOSVM算法选出特征数目的平均值为19.6,而PSOSVM算法和GASVM算法选出特征数目的平均值分别为25和26,是前者的1.28倍和1.33倍。可以得出,GPSOSVM算法相比PSOSVM算法和GASVM算法选出特征子集的数目最少,同时分类精度更高。
在算法效率上,因为不需要进行特征选择和参数优化,SVM算法的运行时间最短,但得到的分类精度较低。另外在数据集的数据量比较大,特征维数比较多的情况下,特征选择的缺失不仅使得分类的精度降低,而且过多的特征数目使得运行速率变慢。这样来看,SVM算法的效率较差。在GPSOSVM算法中,由于在PSO中引入了交叉和变异机制,在每次交叉变异操作后每个个体要进行一次分类,使得算法的时间复杂度相对增加。但实验结果证明,该算法有较强的SVM特征选择和参数优化能力,最终得到的分类精度更高且均衡性更好。另一方面,优化所需的时间虽然增加,但对于同一类型的数据,分类器可以一次优化,多次使用。由于该算法的特征选择能力较强,在使用阶段只需选择较小的特征维数,这样减少了运行时间,提高了使用阶段的运行效率。
综合以上分析,本文提出的GPSOSVM算法无论在提高分类精度、均衡性还是特征选择能力方面表现都最好。
4 结语
针对SVM特征选择和参数进行优化提高分类精度的问题,本文提出了一种改进的基于PSO的SVM特征选择和参数联合优化算法(GPSOSVM)。该算法通过在PSO中引入GA的交叉和变异算子以提高算法的性能,同时避免了GPSOSVM中出现早熟和陷入局部最优的问题。实验表明该算法能得到更高的适应度值,精确得到待分类数据的特征子集和SVM参数,从而得到更高的分类精度而且均衡性更好。但是该算法仍然有改进的空间,例如在迭代过程中如何动态缩小参数取值范围以提高搜索精度等,这将是下一步研究的方向。
参考文献:
[1]BING X, ZHANG M, BROWNE W N. Particle swarm optimization for feature selection in classification: a multiobjective approach[J]. IEEE Transactions on Cybernetics, 2013, 43(6):1656-1671.
[2]BOLNCANEDO V, SNCHEZMAROO N, ALONSOBETANZOS A. A review of feature selection methods on synthetic data[J]. Knowledge & Information Systems, 2013, 34(3):483-519.
[3]RONDING J, HAHN T, DE O L, et al. SCoRS — a method based on stability for feature selection and mapping in neuroimaging[J].IEEE Transactions on Medical Imaging, 2013, 33(1):85-98.
[4]ZHAO Z, ZHANG R, COX J, et al. Massively parallel feature selection: an approach based on variance preservation[J]. Machine Learning, 2013, 92(1):195-220.
[5]ZHANG W, LI C, ZHONG B. LSSVM parameters optimizing and nonlinear system prediction based on cross validation[C]// Proceedings of the 2009 5th International Conference on Natural Computation. Piscataway, NJ: IEEE, 2009:531-535.
[6]庄严,白振林,许云峰. 基于蚁群算法的支持向量机参数选择方法研究[J].计算机仿真,2011,28(5):216-219.(ZHUANG Y, BAI Z L, XU Y F. Research on parameters of support vector machine based on ant colony algorithm[J].Computer Simulation,2011, 28(5):216-219.)
[7]王克奇,杨少春,戴天虹, 等. 采用遗传算法优化最小二乘支持向量机参数的方法[J].计算机应用与软件,2009,26(7):109-111.(WANG K Q, YANG S C, DAI T H, et al. Method of optimizing parameter of least squares support vector machine by genetic algorithm[J].Computer Applications and Software,2009, 26(7):109-111.)
[8]陈渊,马宏伟. 基于蜜蜂算法的支持向量机特征选择和参数优化[J]. 组合机床与自动化加工技术,2013(11):41-43.(CHEN Y, MA H W. Feature selection and parameter optimization of support vector machine based on the bees algorithm[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2013(11):41-43.)
[9]HUANG C L, WANG C J. A GAbased feature selection and parameters optimization for support vector machines[J]. Expert Systems with Applications, 2006, 31(2):231-240.
[10]王维真,熊义军,魏开平, 等. 基于粒子群算法的灰度相关图像匹配技术[J]. 计算机工程与应用,2010,46(12):169-171.(WANG W Z, XIONG Y J, WEI K P, et al. Grey intensity correlated imagematching technology based on PSO[J]. Computer Engineering and Applications,2010, 46(12):169-171.)
[11]石晓艳,刘淮霞,于水娟. 鲶鱼粒子群算法优化支持向量机的短期负荷预测[J]. 计算机工程与应用,2013,49(11):220-223.(SHI X Y, LIU H X, YU S J. Shorttime load prediction based on support vector machine optimized by catfish particle swarm optimization algorithm[J]. Computer Engineering and Applications, 2013, 49(11):220-223.)
[12]段晓东,王存睿,王楠楠,等. 一种基于粒子群算法的分类器设计[J]. 计算机工程,2005,31(20):107-109. (DUAN X D, WANG C R, WANG N N, et al. Design of classifier based on particle swarm algorithm[J]. Computer Engineering, 2005, 31(20): 107-109.)
[13]LIN S W, YING K C, CHEN S C, et al. Particle swarm optimization for parameter determination and feature selection of support vector machines[J].Expert Systems with Applications,2008,35(4):1817-1824.
[14]蔡良伟, 李霞. 遗传算法交叉操作的改进[J]. 系统工程与电子技术, 2006, 28(6):925-928. (CAI L W, LI X. Improvement on crossover operation of genetic algorithms[J]. Systems Engineering and Electronics, 2006, 28(6):925-928.)
[15]CHANG C C, LIN C J. LIBSVM: a library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3):389-396.

