低密度奇偶校验码译码算法性能分析及仿真

王继强 刘翠海 薛蕾蕾 徐涛

摘要：讨论了置信传播（BP）译码算法和在该算法基础上衍生的两种译码算法，对数似然率（LLR-BP）算法和最小和（Min-sum）算法；分析了三种译码算法的性能，并对分析结果进行了仿真验证。结果表明，在译码性能上LLR-BP算法与BP算法相当，前者比后者算法要简单，Min-sum算法虽然较BP和LLR-BP算法相比，损失了一定误码性能，但易于硬件实现，实用性较强。

关键词：LDPC码 信道编码 差错控制 纠错编码 计算机仿真

中图分类号：TN91 文献标识码：A 文章编号：1007-9416（2016）05-0000-00

低密度奇偶校验码（LDPC）是一种线性分组纠错码，当其采用迭代译码算法时，如和积（sum-product） 译码算法，具有逼近Shannon限的良好性能，其译码算法复杂度随码长呈线性增长，非常适合并行实现。正因如此，LDPC码受到了业界的广泛关注，已广泛应用于移动通信、光纤通信、卫星测控通信和数字视频等领域[1] [2]。

构造LDPC码时，其校验矩阵中的非零元素往往很少，正是由于校验矩阵具有这种稀疏的特性，因此出现了多种高效的译码算法，且纠错能力较强。LDPC译码采用的是消息传递（MP）算法，其基本算法有比特翻转（BF）算法和置信传播（BP）算法。BF算法只进行比特位的翻转等几种简单的运算，复杂度较低，因此硬件实现简单，但其性能相对较低，适用于硬件条件受限而性能要求较低的场合；而BP算法是将接收到的信息在变量节点和校验节点之间进行迭代运算，从而获得最大编码增益，因此具有很好的性能，同时复杂度也较高，广泛应用于对性能有较高要求的场合。

本文在介绍低密度校验编码的基础上，研究了置信传播（BP）算法、对数似然率（LLR-BP）算法、最小和（Min-sum）算法等三种译码算法，并对各种算法的复杂度、工程实现的难易度和优缺点进行分析，并对分析结果进行仿真验证。

1 低密度校验编码

LDPC编码的首要条件是构造一个符合条件的稀疏校验矩阵。根据校验矩阵结构不同，通常把LDPC码分为规则LDPC码和不规则LDPC码。规则LDPC码的校验矩阵每行每列的非零元素相同，而不规则LDPC码不受此规则限制。无论哪种，好的LDPC码，必须围绕无短环、无低码重码字、码间最小距离尽可能大的原则构造校验矩阵[3]。

传统的编码方法是将稀疏奇偶校验矩阵H经过高斯消元处理转换为生成矩阵G，再根据G来进行编码。如此的编码方法其生成矩阵的稀疏性难以保证，且会导致编码的运算和存储复杂性大大增加。对于线性编码来说，校验矩阵为H，编码后码字为c，则由校验等式性质H·c=0，所以可以用校验矩阵直接编码，主要的编码方法有高斯消去的直接编码，LU分解编码，部分迭代编码算法等。本文仿真采用高斯消去的直接编码，将m·n校验矩阵H通过高斯消元和列变换改成如下形式H=[I|P]，I为m·m单位矩阵，P为m·（n-m）矩阵，编码后码字c写成c=[s|u]形式，u为输入码字，s为校验码字，由校验等式H·c=0得，I·s+P·u=0，即s=P·u，则由c=[u s]可得编码后码字。

2 LDPC码译码算法

LDPC译码算法是以迭代运算为主，主要是基于二分图[6]结构的消息传递算法。二分图与校验矩阵H相对应，包含三种元素，方形节点、圆形节点及连接方形节点和圆形节点之间的边，对于M×N的校验矩阵H，方形节点Vc=（c0，c1，…，cM-1）称为校验节点，对应于校验矩阵中的列，圆形节点Vs=（s0，s1，…，sN-1）称为变量节点，对应于校验矩阵中的行。如果校验矩阵中的非零位于第i行第j列，则校验节点ci和变量节点sj之间存在一条边，如图1所示，为5×10的校验矩阵二分图表示。LDPC译码时各个节点的置信消息需要在变量节点和校验节点之间互相传递。

3 译码算法性能分析及计算机仿真

从第二节对三种译码算法的分析来看，LLR-BP译码算法虽然与BP算法接近，但是，由于其运算是在对数域进行，因此复杂度有所降低；而MIN_SUM算法则通过采用近似运算来降低复杂度，但是，近似运算导致了该算法性能会有所损耗。

3.1三种译码算法复杂度比较

文献[6]对概率域BP译码算法、LLR_BP译码算法和Min-sum译码算法的计算复杂度进行了对比，各种算法都是针对码率为1/2的（n，2p，p）规则LDPC码进行分析的。如表1所示。

由表1可以看出，在计算复杂度方面，BP算法最为复杂，LLR-BP算法次之，Min-sum算法计算量是最小的。

3.2三种译码算法性能比较

为了对BP算法、LLR_BP算法和MIN_SUM三种译码算法的性能进行分析，本文建立了BPSK系统仿真模型，如图2所示，并以此模型为基础，分析三种译码算法在仿真系统中的性能。

基于图2的系统仿真模型，对三种译码算法性能进行分析。信源部分随机生成，生成的数据u={u1，u2， …，uk}经基于删除信道的迭代算法进行LDPC编码，码长为512，码率为1/2，最大迭代次数为100，编码后得到的码字c={c1，c2， …，cn }进行BPSK调制，调制后将码字c映射成传输码字x={x1，x2， …，xn }。

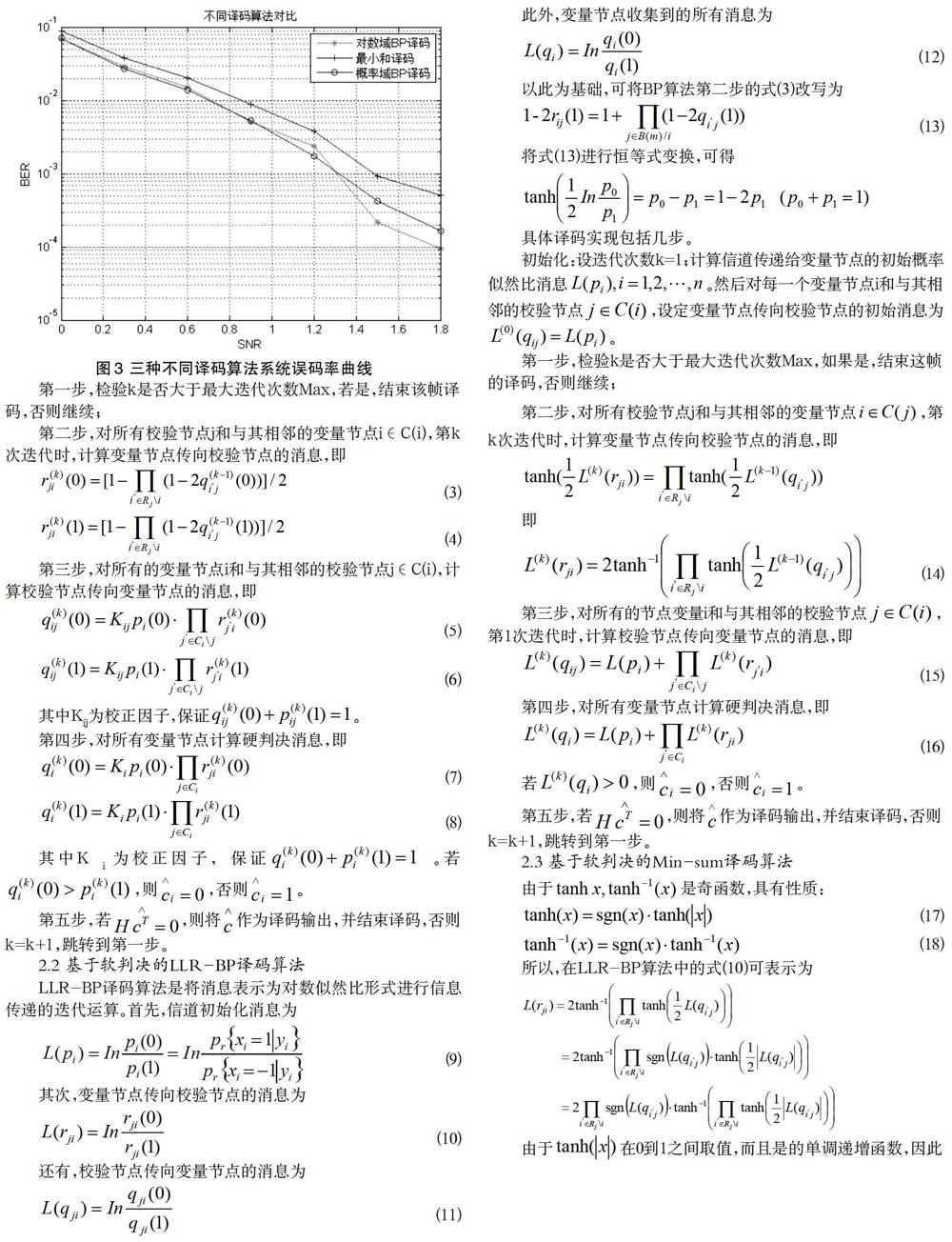
若信噪比取值为SNR = （0：0.2：2），运行系统，可以绘制出采取三种不同译码算法解码后系统的误码率曲线。图3给出了在加性高斯白噪声信道下系统误码率图。

从图3可以看出，BP译码算法和LLR_BP译码算法误码率基本一致，最小和译码算法误码率相对较差。由此可以看出，三种算法中BP算法是基础算法，其译码复杂度最高，但具有最优的译码性能。LLR-BP算法是由BP算法简化而来，通过将原来的运算简化到对数域进行，从而降低了译码复杂度。就译码性能来说，LLR-BP算法最接近BP算法，从图中也可以看出，BP算法与LLR-BP算法的曲线几乎一致。Min-sum算法复杂度最低，与其它两种算法比较译码性能较差，但性能损失不大。所以Min-sum算法复杂度降低，易于硬件实现，实用性较强。因此在实际运用中，我们需要在性能和复杂度上进行整体考虑。

4 结语

低密度校验编码在高速数据传输中有着较好的应用，但是其采用不同译码算法所表现出的译码性能有着较大差异。为此，本文讨论了置信传播（BP）译码算法和在该译码算法基础上衍生的两种译码算法，对数似然率（LLR-BP）算法和最小和（Min-sum）算法；分析了三种译码算法的性能，并对分析结果进行了仿真验证。虽然LLR-BP算法译码性能与BP算法相当，但简化了算法，Min-sum算法虽然较BP和LLR-BP算法相比，损失了一定误码性能，但易于硬件实现，实用性较强。因此，在实际应用中，要根据系统性能要求和硬件条件等因素综合考虑，在译码性能和复杂度之间需要全面衡量，选择合适的LDPC码译码方法，开发相应的硬件产品。本文只是对LDPC码的基础译码算法进行了分析，对不同码长的选择，以及在不同的调制方式和通信环境下系统性能的比较分析未曾考虑，因此还需要进一步完善。

参考文献

[1]沈倩.LDPC码编译码技术研究及其在LTE—A系统中的应用[D].武汉理工大学硕士论文，2012.

[2]彭世章.LDPC编译码技术研究及其在遥测系统中的应用[D].杭州电子科技大学硕士论文，2011.

[3]袁东风，张海刚.LDPC码理论与应用[M].北京：人民邮电出版社，2008.

[4]肖杨.Turbo与LDPC编解码及其应用[M].北京：人民邮电出版社，2010.

[5]刘涛，马沛川.LDPC编译码技术原理及其性能分析[J].通信导航与指挥自动化，2009（4）：12-20.

[6]徐智勇.LDPC码编译码算法的仿真研究[D].东北大学硕士论文，2009.