基于最小二乘法的横纵切碎纸片拼接改进算法

周诗豪

摘要：碎纸片拼接技术对于破损文件修复、司法物证复原等领域有重要的应用。传统人工拼接技术效率低，本文借助算法高效准确地拼接横纵切碎纸片。首先将碎纸片图片导入MATLAB转化为其灰度值矩阵，利用最小二乘原理建立纸片拼接的数学模型，再采用枚举法并结合Lingo软件进行数据分析，找出边缘相似度最高的相邻矩阵，完成单面11×19张碎纸片的拼接。

关键词：碎纸片拼接 最小二乘 灰度值 改进算法

中图分类号：TP391.41 文献标识码：A 文章编号：1007-9416（2016）05-0000-00

1 概念引入

1.1 最小二乘法

最小二乘法是一种数学优化技术，它通过最小化误差的平方和寻找数据的最佳函数匹配。一组数据为 ，。令，在回归分析中称为残差。一般使用作为衡量。

1.2 图片灰度值

在计算机领域中，灰度数字图像是每个像素只有一个采样颜色的图像。我们将19个图片用imread命令读入MATLAB，图片在MATLAB中以灰度图的形式存在。灰度图把白色和黑色之间按对数关系分为0～255一共256个等级，0表示黑色，255表示白色。灰度图是以位图的格式显示，整个图片被分成若干小格。

2 基本假设

1）切割时不丢失信息，纸片的全部信息都包含在所有碎纸片上。2）汉字，英文的字体较规范，每个字所占空间的上下，左右界限一样。3）原图排版无错，不会出现文字错位、错写等情况。

3 模型的建立与求解

3.1 模型的建立

3.1.1 问题的分析

由分析可知，原图中每行左起第一张碎纸片的左边白色区域面积最大，即该纸片从左到右连续出现全为255的列数最多。首先，在209个矩阵中找出其中数值全部为255的列数最多的那11个矩阵。然后，以这11个碎纸片为每一行的行首，分别进行每一行的拼接，得到原文横切割后的11张碎纸片（无序）。最后，将这11条碎纸片进行拼接得到原文图片。

3.1.2 决策变量及目标函数

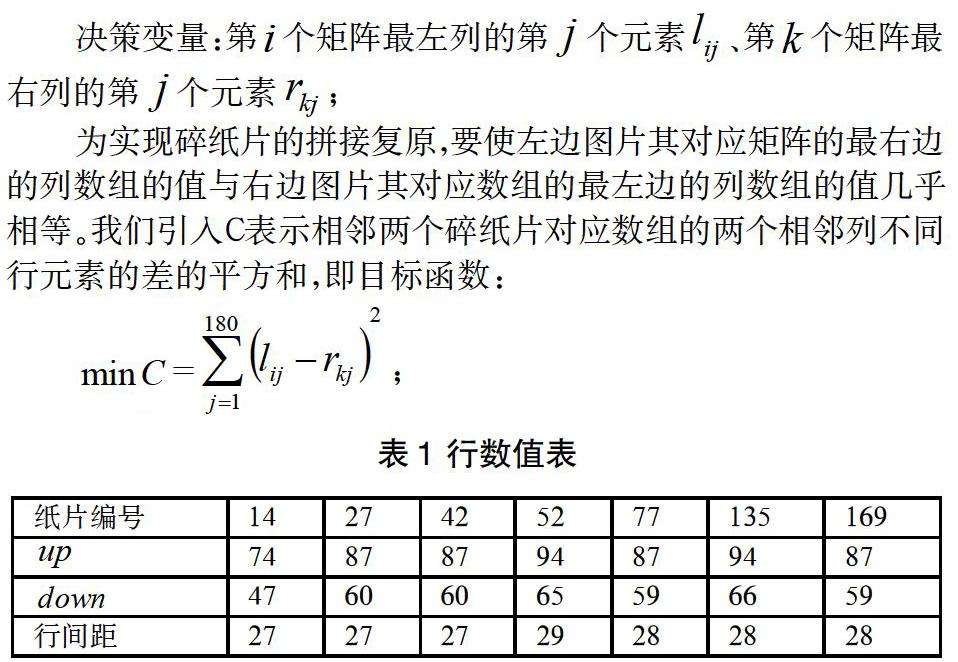
决策变量：第个矩阵最左列的第个元素 、第个矩阵最右列的第个元素 ；

为实现碎纸片的拼接复原，则相邻两张碎纸片的切割处应几乎相同，即左边图片其对应矩阵的最右边的列数组的值与右边图片其对应数组的最左边的列数组的值几乎相等。我们引入表示相邻两个碎纸片对应数组的两个相邻列不同行元素的差的平方和，即目标函数：

=；

3.2 模型的求解

首先，我们利用MATLAB程序求解出排在原文件最左边（即第一列）的11张碎纸片的矩阵编号。

拼接方法：以这11张碎纸片为首，各自从左往右进行行拼接。以矩阵编号a的碎纸片为例，利用枚举法，依次将剩余11*18个未拼接的碎纸片对应矩阵的最左侧列数据与矩阵a的最右侧列数据一一对应，求出11*18个最小二乘结果。值最小时对应的碎纸片拼接出现错误，判断原因是当切割线在字间空白处时，切割处列向量的最小二乘效果很差，无法保证值最小时拼接正确。故利用MATLAB程序循环求出编号和其他11*18个矩阵上边际行数值全为255的整行数，其差的绝对值为，，。比较所有的大小，取值最小且最小的矩阵编号值，此时矩阵编号为的碎纸片排在该行的第二列。用相同的方法求出第三列，第四列直到最后一列的碎纸片的编号。相同的，以另外10张碎纸片为首进行行拼接。此时，拼接仍然出现错误.可能原因如下：

：原文中汉字或英文字母所占空间大小不一。例如，当切割线在词“心里”中间分割，这两张相邻碎纸片的值却有的大。即应正确拼接的图片与已拼接图片的不一定为最小。

：当行首碎纸片中的第一行字是原文中第二行的字时，该碎纸片上方空白处行数较多，不能用于计算比较。应找出其后第二列的碎纸片，用第二列的碎纸片上方空白处行数与未拼接的碎纸片进行比较。

解决上述问题的对应方法：

：我们给定一个合理的空白处行数差值浮动范围。方法：从上方有空白的碎纸片中随机选取7张碎纸片，得出下表相关数据。

表1中表示碎纸片中第二行字上边界的行数，表示第一行字下边界的行数，行间距=-：

行间距的值范围：27～28，则行间距最大差值为2.由于在209张碎纸片中我们只抽取了7张碎纸片且 相邻碎纸片的空白处行数差值行间距，故我们取0～4作为空白处行数差值浮动范围。

：由于行首碎纸片的一行字中包含一个完整的字和一个残缺的字，故可利用残缺的字所提供的信息，通过最小二乘法，找出第二列的碎纸片。而两张纸片拼接在一起大约有三个字的宽度。即拼接了第二张碎纸片后，因段首而缩进两格的第一行会出现第一个字。再对其余的碎纸片进行比较并结合最小二乘结果，得出第三列、第四列直至最后一列的碎纸片。

4 结语

本文提出的拼接模型和相应求解算法的特点在于：综合各方面干扰因素和各种可能出现的情况，即使在文字分布不规范的情况下也可以完成复原。碎纸片拼接采取的是从左向右依次拼接的方法，在自动拼接的过程中，如果出现依次相邻碎纸片拼接错误，那么就可能导致后续一系列的拼接错误。因此，需不断完善算法使得拼接过程不出差错方能确保碎纸片拼接复原的实现。

参考文献

[1]陈冠楠，杨坤涛，陈荣，谢志明.图像灰度值自然对数比率邻域滤波方法[J].计算机应用，2009（7）.

[2]陆健.最小二乘法及其应用[J].中国西部科技，2007（19）.

[3]贾小勇，徐传胜，白欣.最小二乘法的创立及其思想方法[J].西北大学学报（自然科学版），2006（3）.

[4]杨梓艺.纸片拼接技术[J].网络安全技术与应用，2014（5）.