改进粒子群算法在求解柔性作业车间调度问题中的应用
申丽娟

摘要:柔性作业车间调度问题是生产管理中的重要问题。由于建模和计算的复杂性,传统优化方法往往难以得到最优解,而采用粒子群优化算法求解柔性作业车间的调度问题往往可以得到有效解。本文在标准粒子群算法的基础上提出了改进的粒子群算法,在克服标准粒子群算法缺陷的基础上有效提高了其性能,也为其它组合问题的求解提供了理论依据。
关键词:车间调度 粒子群算法 求解柔性
中图分类号:TP301 文献标识码:A 文章编号:1007-9416(2016)05-0000-00
柔性作业车间调度问题[1,2](flexible Job shop scheduling Problem,FJSP),是指带有机器可选柔性的车间调度问题。该类问题已经被证明为NP-hard问题,难以取得最优解。目前,学者们对柔性作业车间调度问题进行了广泛的研究,并提出了许多算法。主要有模拟退火算法(SA)、禁忌搜索算法(TS)、蚁群算法(ACO)、粒子群算法(PSO)[3]和遗传算法(GA)等。其中粒子群优化算法因其具有通用性强、全局寻优和方便实现等优点,在求解柔性作业车间调度领域有一定的应用。本文提出的一种改进的粒子群优化算法,有效提高了标准粒子群算法求解柔性作业车间调度问题时的性能。
1 标准粒子群算法
粒子群优化算法(Particle Swarm Optimization,PSO),也称粒子群算法,是一类基于群体智能的进化搜索计算方法。最早是在1995年由美国的Kennedy和Ebehart在受到鸟群寻找食物行为的启发下共同提出的。算法将所示问题的目标搜索空间与鸟群的飞行空间相类比,为每个粒子制定了与鸟类运动类似的简单行为规则,使得整个粒子群的运动与鸟类觅食具有相似的运动特性,从而用于求解复杂的优化问题。
2 改进粒子群算法求解FJSP
2.1 编码
编码是应用粒子群算法求解柔性作业车间调度问题的关键问题,作业车间调度问题大多采用基于工序的编码,如下所示为一个3个工件在4台机器上加工的部分柔性作业车间调度实例的排序。
粒子的第一维实向量O可表示为(1 1 1 2 2 3 3 3)。其中第一个1表示工件1的第一道工序O11,依此类推;粒子的第二维实向量Xd表示粒子的位置矢量,这里设由(0,5)之间的数随机生产。将粒子的位置矢量Xd按从小到大的顺序进行排序,同时将粒子的第一维实向量O也随着Xd的改变而改变,这样粒子的第一维实向量就形成了一个如下加工工序序列:
每道工序可选择加工时间最少的机器,若是最小加工时间相同可随机选择机器。
2.2 惯性权重的选取
本文采取自然指数自适应的惯性权重选取策略:
式中:G为当前迭代次数;Gmax为最大迭代次数。
3 算法结果比较
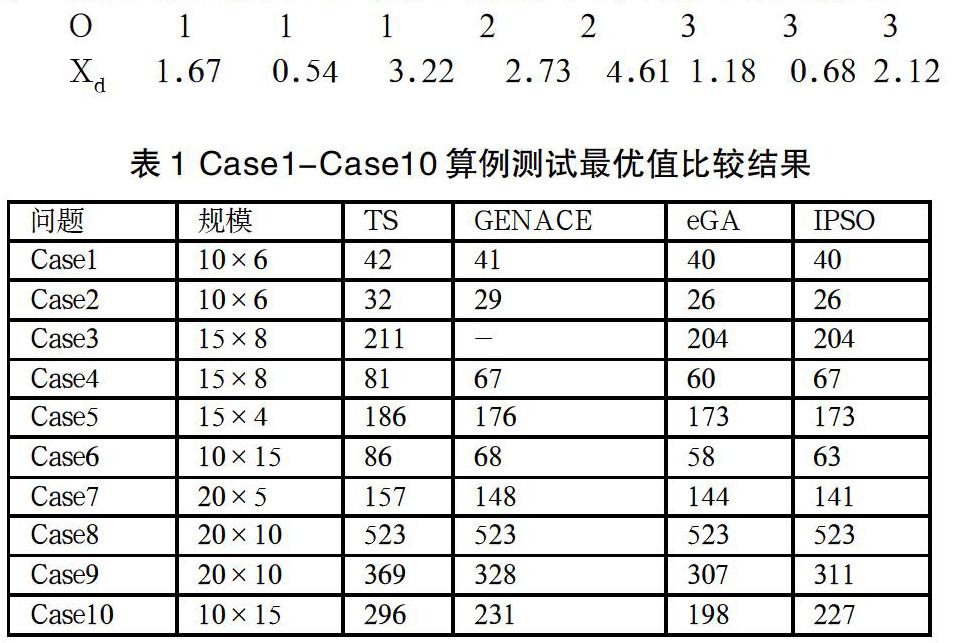
采用10个具有代表性的FJSP标准算例来测试,每个算例的最大迭代次数为200,分别独立运行10次。可以看出,改进粒子群算法最优解总体优于其他三个算法得到的最优解。如表1所示。
4 结语
本文在标准粒子群算法的基础上提出了改进的粒子群算法,通过与标准算例的结果进行对比,证明了本文提出的改进粒子群算法不仅提高了标准粒子群算法求解柔性作业车间调度问题时的性能,也对粒子群优化算法在求解其它组合问题时提供了理论依据,具有重要的理论价值与实际意义。
参考文献
[1]高亮,张国辉,王晓娟.柔性作业车间调度智能算法及应用[M].武汉:华中科技大学出版社,2012.
[2]张国辉,高亮,李培根,张起勇.改进遗传算法求解柔性作业车间调度问题[J].机械工程学报,2009,45(7):145-151.
[3]赵卫.模拟退火遗传算法在车间作业调度中的应用[J].计算机仿真,2011,28(7):361-364.

