流程图布局算法实现

边旭 王明兴 黎俊茂 陈晓晴

摘要：在工作流工具系统中，用户会依据复杂的业务逻辑来建立不同的工作流程图，来描绘不同操作的流程。在这种情况下，用户手工创建的流程图因含有实际的业务逻辑，通常复杂、混乱。为了满足工业工具的实际需要，需要发明一种高效、准确的流程图自动布局方法，快速合理布局复杂的流程图，准确体现数据的流向和清晰展现节点中蕴含的逻辑关系。

关键词：流程图 布局 算法

中图分类号：TP391 文献标识码：A 文章编号：1007-9416（2016）05-0000-00

1现状分析

随着互联网的快速发展和社会各领域信息化水平的提高，数据量正以史无前例的速度井喷。在大数据时代，处理海量数据的抽取和加工的工作流工具系统有着非常重要的工业用途。在工作流工具系统中，用户会依据复杂的业务逻辑来建立不同的工作流程图，来描绘不同操作的流程。在这种情况下，用户手工创建的流程图因含有实际的业务逻辑，通常复杂、混乱。为了满足工业工具的实际需要，需要发明一种高效、准确的流程图自动布局方法，快速合理布局复杂的流程图，准确体现数据的流向和清晰展现节点中蕴含的逻辑关系。

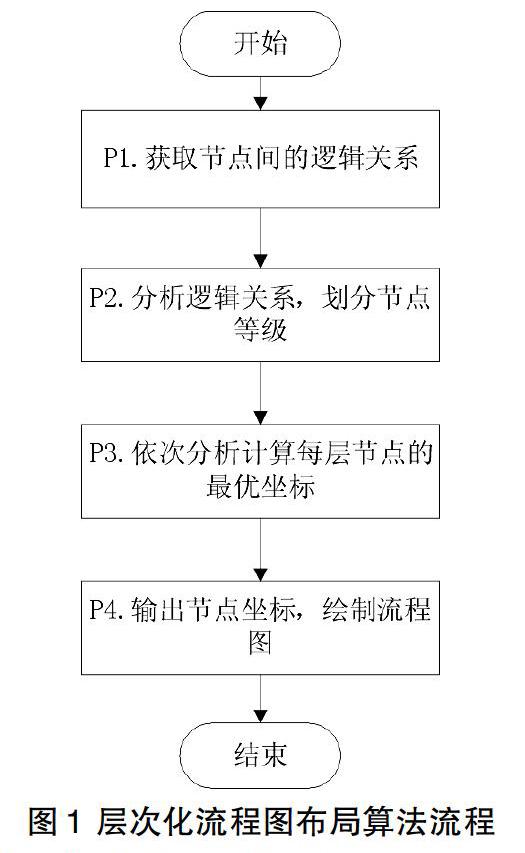
流程图布局算法有多种，国际商业机器公司[1]和恒生电子股份有限公司[2]都提出应用于工业的突出主线的流程图自动布局方法。另一方面，层次化的流程图布局算法也得到了广泛关注，多种布局算法[3]根据拓扑顺序（概念见图1）对流程图进行层次化布局。

本方法的输入是一组逻辑关系数据。P1：从已知数据中抽取出节点信息和它们的逻辑关联；P2：分析节点的逻辑关系，为节点们划分等级；P3：优化级别相同的节点们的排列方式，达到合理布局，并计算节点们的坐标值；P4：根据坐标值，建立绘制流程图。

1.1相关研究

学术界，存在多种流程图层次化布局算法，它们都遵循了图1的流程。不同的是，在P3步骤，不同的方法，采用了不同的解决方法。其中最具代表性的是Sugiyama[3]的算法，它通过用矩阵来表示流程图的节点关系，来分析优化节点的布局，让流程图的交叉线最小，连线距离最短。Sugiyama算法的流程图如图2。

已有的层次化流程图布局算法，它们的流程图分析算法（P3步骤）过于复杂，无法满足工业高效、简洁的需求。本方法发明了一种全新的流程图布局的分析优化方法，高效、简洁地实现了蕴含的复杂逻辑关系的工作流节点的层次化布局，满足了大数据工业应用的工作流程图布局要求。

1.2 本文实现方法和效果

本发明实施了在大数据处理的工作流的应用场景下，一种准确、高效的流程图布局分析优化算法。在大数据工作的工作流工具里，每个工作节点间存在复杂的逻辑关系，而用户很难将节点合理的分布在工作流页面里。在这种情况下，需要一个高效、准确的流程图布局分析优化算法，快速合理布局层次化的复杂流程图。

2算法实现

基本概念定义：逻辑关系。逻辑关系的含义非常丰富，在我们的方法里，它特指事件（抽象为节点）间建立的带有顺序性、业务逻辑性的关联关系。例如：一个逻辑关系，表明事件A和B关联，且只有A事件发生，B事件才有可能发生。

2.1逻辑节点（Node）

每一个事件，我们都把它抽象为一个节点。当节点间包含逻辑关系，我们称这样的节点叫逻辑节点。

每个节点里都包含以下信息：节点的名称（NodeName），子节点的列表（List outNodes），父节点的列表（List inNodes），出度（outNum），入度（inNum），层次（Level）。

子节点：当前节点的下一个逻辑节点（outNode）；

父节点：当前节点的前一个逻辑节点（inNode）；

入度：一个逻辑节点的父节点的个数；

初始逻辑节点：入度为0的逻辑节点是初始节点。

2.2连线（Link）

描述两个节点间的逻辑关系，每条连线里包含它的起始节点（startNode）和结束节点（endNode）.

下面给出一个例子来描述上面定义：

例1：一组逻辑关系{，抽象后，我们得到8个节点{A、B、C、D、E、F、G、H}和9条连线{（A，D）、（A，E）、（B，F）、（B，E）、（B，H）、（C，G）、（D，G）、（D，H）、（E，H）}。

2.3等级（Level）

一个逻辑节点在所给逻辑关系中的级别，它包含了这个逻辑节点在逻辑关系中的顺序特性。等级越低的逻辑节点在逻辑关系中，代表越先发生的事件，往往是前驱事件。

2.4深度优先遍历

是数据遍历的基本方法之一，在本方法中指按照逻辑关系所蕴含的顺序，从逻辑的起始节点到结束节点遍历的方法，并且，尽可能遍历到没有子节点的逻辑节点为止。并且，不同于其他深度遍历方法，我们的深度优先遍历，会重复遍历节点。

例如：在上面的例子中，起始节点是A、B、C，按照深度遍历。起始点A下面的遍历，依次通过的连线为（A，D）、（D，G）、（D，H）、（A，E）、（E，H）， 因此遍历节点顺序为，同理，B的遍历节点顺序为C的遍历节点顺序为。

3一组逻辑节点等级划分方法

给定一组逻辑关系，本方法提取每个事件元素作为一个节点，通过分析已知的逻辑关系， 给这些逻辑节点划分等级，设置等级值（level）。

方法实施核心过程详细介绍如下：

方法的输入是从数据中提取的一组逻辑节点（Nodes）和它们的逻辑关系（Links），如例1。

P1：

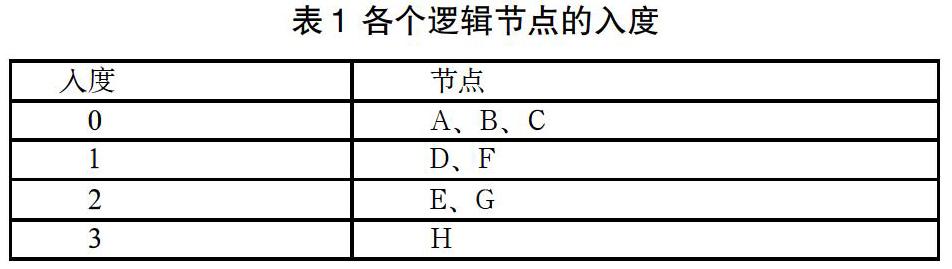
根据给定的逻辑关系，其蕴含了节点之间的逻辑顺序，我们根据这些信息，首先计算每个节点的入度。根据入度的定义，例1中各个逻辑节点的入度的值见下表1。

根据表1，我们可以定位，初始节点是A、B、C节点。

P2和P3：循环遍历设定逻辑节点的等级（Layer算法）

当我们定位了逻辑关系中所有的初始节点，我们依次对每个初始节点进行深度优先遍历，在这个遍历过程中，我们要依次设置各个节点的等级。因此，P2和P3步骤是循环进行的，每次遍历一个节点，都要对其的等级进行设定。

在Layer算法的遍历中，我们遵循以下三个原则：

（1）起始逻辑节点的等级是1；（2）依次遍历初始节点，沿着其连线深度遍历，每个当前逻辑节点的等级等于父节点的等级加1；（3）当一个节点有不止一个父节点的时候，它的等级由等级最高的那个父节点决定。

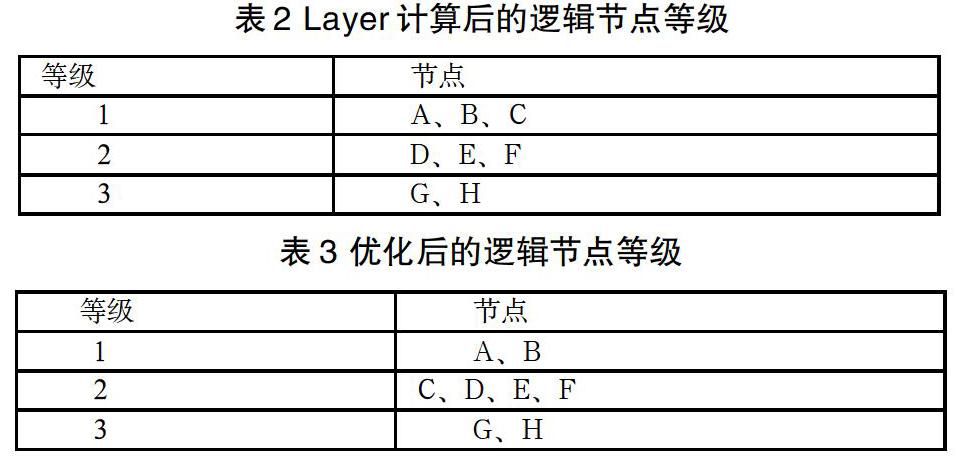
Layer算法的详细流程：例如例1：依次遍历A、B、C三个初始逻辑节点，依据上面的遍历和等级定义原则，各节点的等级如表2。

其中，节点H有三个父节点B、D、E，因此它的等级由等级较高的D和E决定，为3。

P4：优化逻辑节点的等级

例1中，我们注意到初始节点C，有且仅有一个子节点G；即，逻辑节点C只和一个逻辑节点G在逻辑上具有关联性，它们是息息相关的。然而，在Layer方法计算得到表2中，节点C和G的等级差异为2，无法正确体现逻辑节点间紧密相关的关系。对这类情况，P4步骤对节点的等级进行了优化。

根据上述的流程，我们当且仅当，优化初始节点和它最近级别的子节点的等级差距大于1的时候，对初始节点的等级进行优化。例1中，虽然初始节点B和它的子节点H的等级差距为2，方法并不会对逻辑节点B进行优化，因为它的其他子节点E和F的等级为1，和它非常接近。

经过调整，我们得到最终的优化后的各个逻辑节点的等级如表3。

4结语

在分析研究现有流程图布局的基础之上，本文提出了一种新的流程图布局的算法。并将该算法应用在了实际布局上，效果较已有方法更好。

参考文献

[1]专利：处理图形对象的方法、设备及系统，国际商业机器公司，申请号：200910132268.X.

[2]专利：实现流程图自动调整布局的方法及装置，恒生电子股份有限公司，申请号：200910246003.2.

[3]K.Sugiyama，S.Tagawa，and M.Toda. Methods for visual understanding of hierarchical system structures.SMC-11（2）：109–125，February1981.