基于静态小波分解的空间滤波信号降噪方法
陈闪闪 朱春雪 朱俊臣 朱志雄 曾祥楷

摘要:过零点法是简单、高效率的提取空间滤波传感器输出信号中心频率的方法,但是过零点方法抗噪性能较差。针对这个问题本文提出了基于静态小波分解技术的滤波方法对准正弦信号降噪。该方法是根据中心频率的预测值,控制A/D转换采样率,对采集到的准正弦信号进行N层的静态小波分解,将信号的中心频率划分到某一层内,对这层信号再利用过零点方法测中心频率。试验表明,该方法是可以有效的提高中心频率测量精度。
关键词:空间滤波器 过零点法 中心频率 静态小波分解
中图分类号:TN911 文献标识码:A 文章编号:1007-9416(2016)05-0000-00
1 引言
空间滤波测速法(Spatial-Filtering Velocimetry, SFV)是利用空间滤波器技术实现速度测量的方法。因其结构简单,对光源要求不高得到了广泛的应用。在该方法中,准确测得空间滤波器输出的准正弦信号中心频率是保证系统能够准确测速的关键。所谓准正弦信号是指幅度和相位均随机的信号,其能量集中在中心频率处。
在现有中心频率提取方法中,过零点计数法测频率是在数字设备中,利用插值技术得到信号过零点坐标,将用过零点坐标计算一段时间内信号的平均频率作为此段信号的中心频率的。对于连续周期波形,过零点计数技术是确定中心频率最简单的方法,且过零点计数法的提取中心频率速度快[1]。但是,此方法抗噪声能力弱,尤其在过零点处的噪声,特别容易造成粗大误差。
小波分析是对傅立叶分析的继承,是一种时间-尺度定位技术,能够对信号进行频域分层分析。为了瞬时、准确地提取出中心频率,本文研究了基于静态小波分解的自适应滤波技术对空间滤波器输出的含噪信号进行降噪处理,再用过零点计数法提取降噪后信号中心频率的方法,这样提取的中心频率具有更好的精度。另外,小波分析具有局部性,可以选择很短时间的信号进行自适应降噪处理,这样保证了中心频率提取的瞬时性。在阐述新方法前,有必要对空间滤波器及其输出的信号特点进行简述。
2 空间滤波测速原理及其输出信号特点
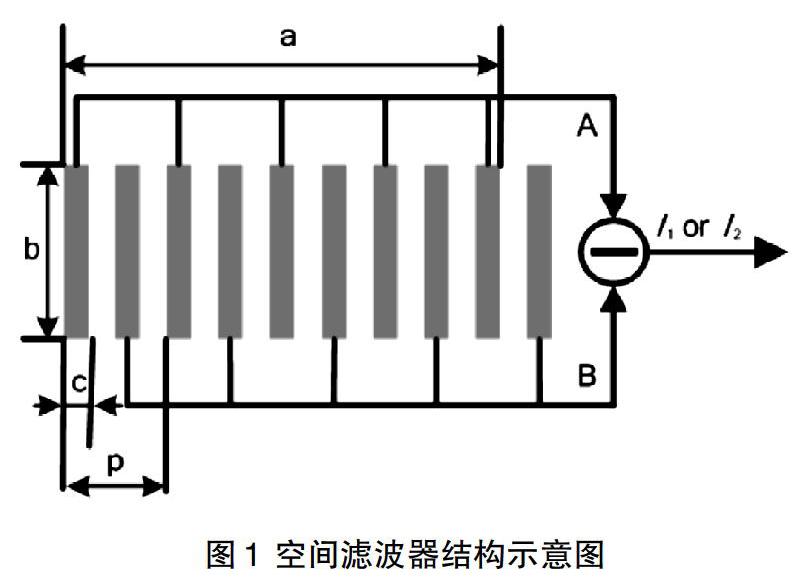
差分型空间滤波器可以有效的消除直流分量及各偶数次谐波分量而得到了较多应用,文献[2]中所用差分型空间滤波器结构如图1所示。
A支空间滤波器的透射区域分布函数减去B支空间滤波器的透射区域分布函数,结果就是差分空间滤波器透射区域分布函数。其归一化的理论空间功率谱为:
式中,c为单个光电池感光面积,p和a见图1中所示。差分型空间滤波器具有窄带通空间滤波的作用,并且仅仅剩下奇次谐波分量。功率谱在?0=1/p处取得最大值。这样特性的滤波器决定了其滤波后的信号也是窄带信号。
将图1中阴影部分设计成光电池时,空间滤波器既有空间滤波作用又有光电转换作用。当空间滤波器用于测速时,输出信号等价于图像的光强分布函数和空间滤波器透射函数的卷积,最终输出时域信号的理论功率谱密度为[4]:
上式中,f是时域频率,?是空域频率,v是线速度。根据时域频率与空间频率的关系最终得到速度和时域中心频率f0的关系:
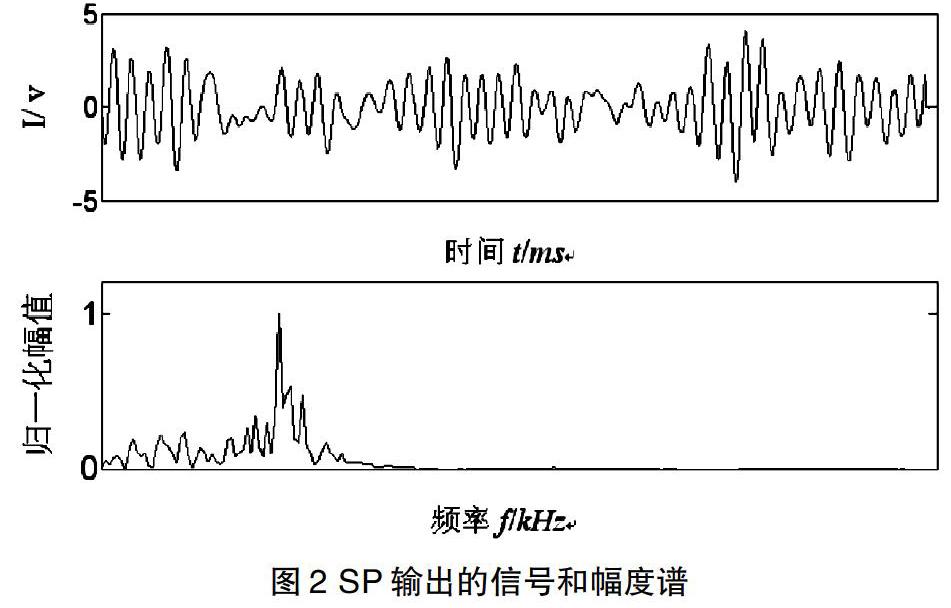
由(3)式可知,运动物体每移动p距离,信号就对应出现一个波形周期。由以上分析知,只要测得SF输出信号的中心频率就可以计算出对应的速度。图2是空间滤波器输出信号的时域仿真波形及其对应的幅度谱。信号幅度和相位的随机性由运动体反射面的反射系数分布特性和速度决定。
从上图2可以看出,准正弦信号的幅度和相位是随机的,其频谱是窄带谱,包含有低频噪声和高频噪声,主要是低频噪声的影响,使得信号的周期不均等,直接利用过零点方法测中心频率会有很大的误差。针对准正弦信号的谱特性,可以利用小波分解进行自适应滤波,尽可能的滤除低频和高频噪声,使得幅度谱尽可能的变窄。
3 基于静态小波分解的空间滤波信号降噪方法
3.1多分辨分析和静态小波分解
小波变换的本质是用不同频带的小波对信号的一种逼近,因此小波分析具有多分辨率分析特性。多分辨分析的本质是按照信号带宽对信号进行高通和带通镜像滤波器滤波,得到高频成分(细节部分)和低频成分(近似部分),然后对低频成分继续应用镜像滤波器进行滤波,又得到低频部分的高频成分和低频成分,如此进行,就可以实现对信号的多分辨率分析。多分辨分析的原理图如图3所示[3]:
Cj是低频系数集,是Dj高频系数集——小波变换系数。一般的,根据需要,多分辨分析进行到一定层数就可以了,这样,信号最终被分解成低频的近似层和高频的细节层,将无穷层分解化成为了有限的几层分解。
静态小波分解(Stationary Wavelet Transform,SWT)的基本思路是对信号进行镜像滤波,但是滤波器要随着分解层数改变而改变,如对序列C1进行滤波时,序列C1不变,对镜像滤波器组经行上2插0处理,从而使得镜像滤波器组的谱变成为原来的1/2的宽度,其能够对C1进行高低通镜像滤波,得到长度和原始信号序列长度相近的序列C2和D2,对C2继续进行上述滤波,就会得到各层分解序列[4]。
3.2基于静态小波分解的空间滤波信号的降噪方法
基于SWT的空间滤波信号的降噪原理,要从离散时间信号的傅里叶变换对应的是归一化频率这一基本事实谈起。所谓的归一化频率是[5]:
F是物理频率,fs是采样频率,f是归一化频率,显然,对于确定的物理频率,其对应的归一化频率由采样频率fs决定。上面对多分辨率分析、静态小波分解都是在离散时间下进行的,所以其频率是归一化的。通过控制采样频率,就可以将镜像滤波器组的归一化频率的幅度谱控制在某一确定的频段内,同样的只要控制对信号的采样频率就可以准确的控制离散序列的归一化频率频谱在某一确定的频段内,而改变采样频率是简单易行的。所以,基于SWT的空间滤波信号的降噪原理如下:选择合适的母小波,确定要进行静态小波分解的层数M,预计将准准正弦信号的中心频率划分到第N层的细节层,那么,即可根据下面的等式计算出对应的采样频率:
上式中,fc'是中心频率的预测值,可以用前一时刻得到的中心频率作为预测值。对信号进行Fs频率的采样,并对之进行M层静态小波分解,得到第N层的细节信号。显然,第N层细节信号的中心频率与原始信号中心频率是一样的,但是该层信号的低频噪声与高频噪声得到了很好的抑制。对第N层的细节信号用过零点方法提取信号的中心频率,精度会比直接对原始信号利用过零点技术提取的中心频率的精度要好。
4 仿真实验和分析
利用空间滤波信号进行仿真实验。在进行静态小波分解时要选择母小波和分解层数,经过试验,在本方法中选择了“db4”作为母小波,进行6层分解,并使得中心频率包含在第六层的细节部分,设中心频率是第六层的中点频率,那么对应的采样率就是:
那么,经过以上采样频率的设置,经静态小波分解后中心频率落在了在了第六层的细节部分,只要提取出第六层细节信号,就得到了对准正弦信号的小波分解滤波信号。对滤波后的信号用过零点法测中心频率。
实际中,为了提高中心频率提取的瞬时性,数据长度不宜过长,同时,为了提高中心频率的提取精度,数据又不宜过短,在此,选择512个点的数据长度。下图4是得到的一段中心频率理论值为 2.0106kHz的准正弦信号及其对应的幅度谱。
直接对其进行过零点测中心频率,提取值为2.1100kHz,相对误差为4.9410%。对准正弦信号进行静态小波分解滤波后所得第6层细节信号及其幅度谱如图5所示。
从图5中可以看出,信号波形变好,幅度谱变窄。为了比较幅度谱的区别,现将两者画在了一起,如图6所示,在图6中点画线代表准正弦信号的幅度谱,实线代表着滤波后信号的幅度谱,比较两者可以明显的看到,经过静态小波分解滤波,信号的低频和高频噪声均得到了很好的衰减,尤其是低频噪声,得到了很好的滤除。
对图6滤波后的信号用过零点方法测中心频率,提取值为2.0199kHz,相对误差为0.4598%。
5 结语
本文提出了利用静态小波分解实现对准正弦信号降噪滤波的方法,在该方法中根据中心频率预测值,合理地选择采样频率,对信号进行静态小波分解,即可将中心频率划分到某一层内,对该层信号用过零点法测中心频率。最后的实验表明,本文研究的新方法对准正弦信号去噪效果比较好,尤其是对信号中的低频噪声作用十分明显,对高频噪声也有一定的抑制作用;另外,试验结果表明,对经过静态小波分解滤波后的信号利用过零点方法测中心频率的误差比直接对准正弦信号利用过零点方法测中心频率的误差要小。
参考文献
[1]郑丽娜.航空相机高精度速高比测量技术的研究[D].中国科学院大学,2013.93-94.
[2]曾祥楷,陈阳等.空间滤波转速遥测中旋转方向的辨识方法[J].光学学报,2015,35(6):0612001-1~0612001-9.
[3]封常生.小波分析在信号处理中的应用[D].上海:上海交通大学,2007.18~19.
[4]高成,董长红,郭磊等.Matlab 小波分析与应用[M].北京:国防工业出版社,2007.162~165.
[5]胡广书.现代信号处理教程[M].北京:清华大学出版社,2004.300~301.

