不等关系与相等关系其实是统一的

刘帅　孔凡哲

与方程一样，不等式也是表达现实世界数量关系的一种数学表现形式，是反映客观事物变化规律及其关系的数学模型。

不等式（组）是“数与代数”领域的重要内容之

，具有承上启下的作用，它上承一元一次方程、二元一次方程组，下接一次函数等内容，不等关系与相等关系其实是统一的，二者不仅都是刻画数量关系的有效模型，而且可以互相转化。

一.体会现实世界中的不等关系

在大千世界中，量与量之间的关系是由相等关系和不等关系构成的，在方程的学习中，我们学会了用相等关系解决生活、工作巾的诸多问题，其实，小等关系也是刻画现实世界中的数量关系的有效模型，不同的是，相等关系刻画的是“静态的数量关系”，不等关系刻画的是“动态的数量关系”。

下面，让我们来看看交通中常见的不等关系。

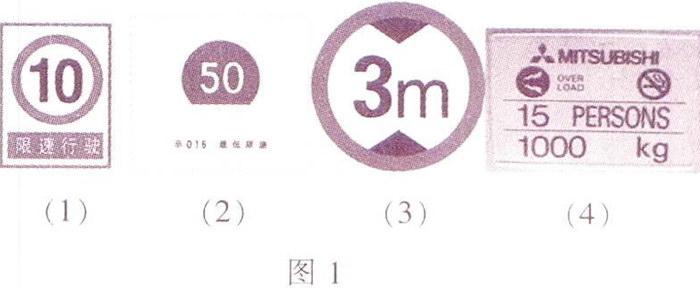
限速，如同l（1），该图标的意思是速度不可越过10km/h，即V≤10km/h；如图l（2），该图标的意思是速度不可低于50km/h，即V≥50km/h.

限高，如图1（3），该图标的意思是车的总高度不可超过3m即h≤3m，

限重，如图1（4），该图标为电梯的标识牌，表示此电梯的载重量不可超过l000kg，即G≤1000kg，人数不可以超过15，即N≤15。

在限速120km/h的高速公路上，按照规定正常行驶的汽车，其行驶速度仪存一些时刻等于120km/h，而在更多的时刻是不等于120km/h的，也就是说，等于120km/h是静态的、短暂的，而不等于120km/h是动态的、持久的.

不仅交通中存在大量不等关系，生活中的许多方面，诸如食品安全、购物、建筑等，也存在着大量不等关系。

建议你在课余时间，与同学一起去观察、发现，并且可以用简单的不等式将小等关系表示出来！

二.不等关系与相等关系的统一性

不等关系与相等关系是普遍存在的，不等关系与相等关系具有内在的必然联系，也可以说是统一的。

对于典型的不等关系a>b，如果我们设c=a-b，那么，不等关系a>b就与相等关系a=b+c等价，其中，c是一个正数，

更进一步说，a>b等价于“存在一个正数c，使得a=b+c”，a≥b等价于“存在一个非负数c，使得a=b+c”

利用上面的等价关系，可以轻松地将不等关系转化为相等关系，

例如，对于“如果a>b，那么，对于数c，有a+c>b+c”，可以这样证明：

如果存在一个正数d，使得a=b+d，那么，对于数c，有a+c=b+d+c=（b+c）+d，这意味着，存在一个正数d，使得a+c等于b+c与d的和，从而，a+c>b+c，

三.在建立不等式过程中进一步体会建模思想

购物是我们在现实生活中不可或缺的活动之一，为了吸引更多人到商场购物，卖家经常会设计各种各样的促销活动，究竟哪种方案最优惠呢？我们一起用不等式模型来分析一下！

例某商店5月1日举行促销优惠活动，当天到该商店购买商品有两种方案，

方案1：用168元购买会员卡成为会员后，凭会员卡购买商店内任何商品，一律按商品价格的八折优惠。

方案2：若不购买会员卡，则购买商店内任何商品。一律按商品价格的九五折优惠，

已知小敏5月1日前不是该商店的会员，

（1）若小敏不购买会员卡，所购买商品的价格为120元时，实际应支付多少元？

（2）请帮小敏算一算，所购买商品的价格在什么范围内时，采用方案l更合算？

解析：（1）120×0.95=114（元），

（2）第一，发现问题中的不等关系，方案1所花钱数不高于方案2所花钱数。

第二，用不等式表达不等关系，

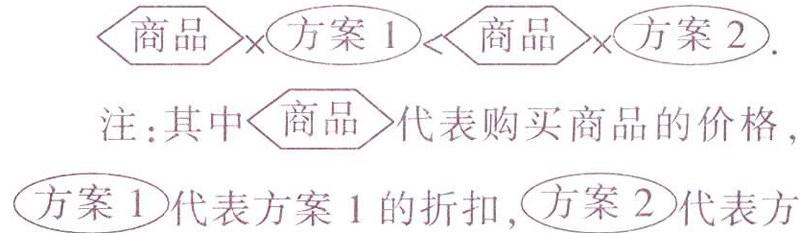
购买商品的价格×方案1的折扣<购买商品的价格×方案2的折扣，

第三，用符号语言表达不等关系，

第四，用含有未知数的不等式表达不等关系，

设购买商品的价格为x元，由题意得：

0.8x+168<0.95x，

将0.8x移项并与0.95x合并，得O.15x>168。将未知数的系数化为l，得x>l120，

所以，当购买商品的价格超过l120元时，采用方案1更合算，

经历了上面的分析过程，相信你会利用不等式这一数学模型解决优惠方案这类问题了，今后遇到类似的问题时，要注意选择最优惠的方案哟！