分步构建模型 突破晶体教学的瓶颈
马薇
摘要:晶体结构教学中常因内容抽象使得教学效果不佳,作者采用分步构建模型的方法,帮助学生逐步提高空间想象能力,从而较好的突破这一教学难点。
关键词:晶体结构;构建模型
文章编号:1008-0546(2016)06-0065-04 中图分类号:G632.41 文献标识码:B
doi:10.3969/j.issn.1008-0546.2016.06.022
晶体结构的教学能够帮助学生全面地认识物质的结构,体会结构对物质性质的影响,但该部分教学内容较为抽象难懂,对空间想象力要求较高,学生普遍感觉学习难度较大。王伟[1]等统计了2007~2013年“晶体结构与性质”主题的高考考点发现,了解、识记常见物质的晶胞结构并在此基础上进行相关计算是本部分考核的一个重点,而这也是教师普遍感觉较难落实的教学问题。笔者通过教学实践发现,分步构建模型是突破这一难点的很好的方法。
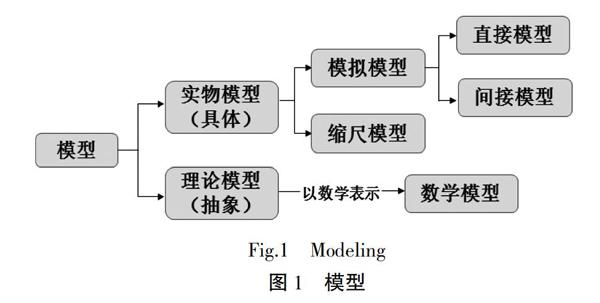
模型是一种重要的科学方法[2],在化学研究和科学发展中发挥了重要的作用。不仅如此,模型也是一种重要的学习工具,它可以帮助学生理解一些抽象的科学概念,掌握理论和解释现象。《美国国家科学教育标准》中的对模型的表述为:模型是与真实物体、单一事件或一类事物相对应的而且具有解释力的试探性体系或结构。沈文选[3]认为模型大体分两类:实物模型(具体模型)和理论模型(抽象模型)。实物模型可以分为模拟模型和缩尺(肖像)模型。模拟模型可再分成直接模拟和间接模拟。理论模型既可以是实物、现象、过程的抽象表示形式,也可以是我们所要描述的对象以及分析他们行为方式的抽象表示形式。当一个对象的理论模型以数学表示其一组规则和定律时,一个数学模型就呈现出来(见图1)。
教学中笔者按照这个思路,尝试采用先实物模型再理论模型的方法分步构建晶体模型,逐步培养学生的空间想象能力,收到了较好的教学效果。
在构建模型之初,教师首先需要做的是对高中化学常见晶体结构模型的整合。
一、高中化学晶体模型的整合
1. 分子晶体的模型
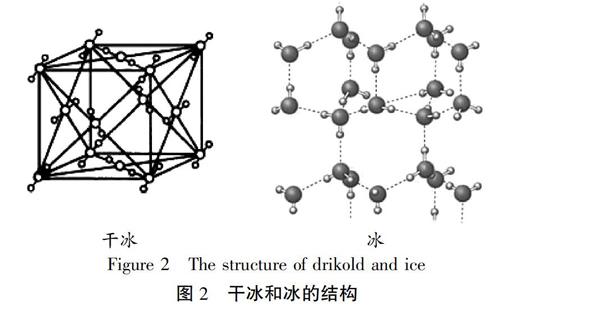
人教版选修3课本中涉及的分子晶体模型主要包括分子间以范德华力结合的干冰和分子间主要以氢键结合的冰两种结构(见图2),课本中给出了干冰的晶胞和冰中水分子连接方式的示意图,并没有给出冰的晶胞。
2. 金属晶体的模型
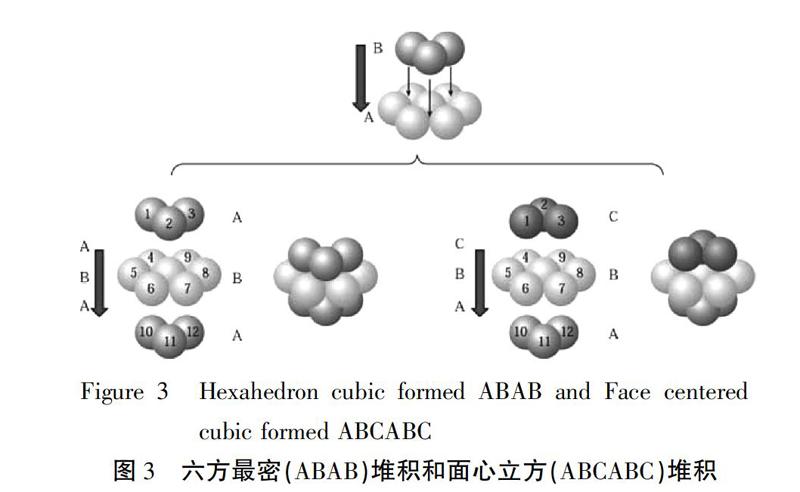
人教版选修3课本中涉及的金属晶体堆积模型主要分为简单立方堆积、体心立方堆积、面心立方堆积、六方最密堆积四种,其中六方最密(ABAB)和面心立方(ABCABC)两种堆积方式学生学习时较难理解(见图3)。
3. 离子晶体的模型
人教版选修3的课本中只给出了NaCl型、CsCl型、CaF2型三种典型离子晶体的结构,没有给出ZnS的晶体模型(见图4),教师在教学时需要补充(原因笔者将在后文中叙述)。
如果学生没有理解、记忆、掌握以上内容,在此基础上进行的晶体化学式推断、晶体密度、晶胞体积、阿伏加德罗常数(NA)、晶胞棱长、晶胞粒子间距离、空间利用率等晶体结构相关计算不啻天方夜谭。在教学之初,这些堆积方式和粒子间的相对位置关系仅靠看书上的插图和死记硬背根本不能达到预想的教学效果,恰当的构建实物模型能够帮助学生更好地理解和体会这部分内容。
二、构建实物模型
晶体模型是一种实物模型,它能够直观清晰地展示晶体中粒子之间的相对位置关系,对帮助学生构建空间想象能力、了解并掌握晶体的结构有极大的帮助。很多学校采用购买现成的晶体模型进行教学,可是据不完全统计,使用情况并不乐观。由于经费原因,中学化学实验室并不能购齐所有的晶体模型,即便购全,每种也只有有限的几个,不能保证学生人手一个。另外,使用现成的晶体模型教学的最大弊端是学生无法深刻理解晶胞中粒子之间的位置关系和个数配比,只能陷入机械的记忆。而这也让学生认为物质结构的学习抽象难懂、枯燥无味,学习兴趣不高,学习效果大打折扣。
美国教育家苏娜丹戴克说:“告诉我,我会忘记,做给我看,我会记住,让我参加,我就会完全理解。”所以,让学生利用简单易行的材料亲自动手组装晶体模型,不但节约成本,保证每个同学都能使用,而且能够帮助其建立起对晶体结构的深层理解和合理的空间想象力,同时大大增强学习的趣味性,激发学生的学习兴趣,有效地解决了之前的问题。这一做法其实也是教材的编写意图,在人教版选修3的课后习题中也提到“用橡皮泥、牙签等材料,自己动手制作晶体模型”。
笔者在教学中尝试让学生用泡沫塑料球和毛绒条扭扭棒自己拼插各种晶胞模型(见图5),所用材料廉价易得,制作安全简单,取得了良好的教学效果。
金属的堆积模型可以使用泡沫塑料球、用502胶直接粘合制作。在亲手制作过程中,学生能够体会非密置层、密置层的二维堆积过程;了解非密置层在三维空间进行简单立方堆积、体心立方堆积的区别;对之前很难理解的密置层在三维空间的ABAB、ABCABC两种堆积过程有更深刻的体会;平时难以用语言描述的六方最密堆积的晶胞也能亲手制作并一目了然地呈现在学生眼前(见图6)。在实物模型的帮助下,学生能够根据小球相切的情况,轻松掌握晶胞结构中微粒之间的距离与晶胞棱长的相互关系。至此,大部分学生能够结合已有数学知识,进行简单的晶胞综合计算,程度较好的学生甚至可以顺利地推算出六方最密堆积晶胞的空间利用率为什么是68%!
由此可见,“看”模型和“做”模型有着本质的区别,学生亲自动手组装模型的过程是其对于晶体结构的深化理解的过程。微粒在晶胞中的相对位置、微粒之间的距离关系等都在学生在制作模型的过程中自然而然地形成。几个相同的晶胞无隙并置在一起,每种微粒的配位数很自然地呈现在了学生眼前。这是学生利用实物构建空间想象能力的关键步骤,也为脱离实物模型构建理论模型提供了前题。
三、构建理论(数学)模型
晶体结构的学习不能一直依靠实物模型,构建适当的理论模型对于培养学生的空间想象能力、提高学生的科学素养有着重要的作用。结构化学中,晶胞具体形状大小由它的三组棱长a、b、c及棱间交角α、β、γ(合称为“晶胞参数”)来表征,这种理论模型对于高中学生而言过于深奥。笔者结合教学内容,利用学生比较熟悉的“均摊法”构建晶体结构的数学模型,教学效果良好。
1. 均摊法简介
均摊法是在计算晶胞中的微粒时应分析一个微粒被多少个晶胞共享的方法,常见的平行六面体晶胞中的微粒通常这样均摊计算:
①处于顶点的微粒,同时为8个晶胞所共用,每个微粒有1/8属于该晶胞;
②处于棱上的微粒,同时为4个晶胞所共用,每个微粒有1/4属于该晶胞;
③处于面上的微粒,同时为2个晶胞所共用,每个微粒有1/2属于该晶胞;
④处于晶胞内部的微粒,不与其他晶胞共用,完全属于该晶胞。
2. 利用均摊法构建晶体结构的数学模型
笔者以均摊法为基础,把晶胞中的微粒分为四种对应四个典型位置的点——点、点、点、1点,分别对应晶胞中的顶点、棱上点、面上点、体心点(见表1)。
(1)离子晶体晶胞的数学模型
表2为离子晶体晶胞的模型:
晶体结构数学模型的构建过程中巧妙地把学生已经较为熟悉的“均摊法”与晶体的结构结合在一起,用熟悉的事物描述陌生的问题,能够有效地提高学生对难点的接受程度。掌握这套模型后,学生可以能够快速、简洁地使用数字描述出晶体中微粒的位置,同时与头脑中的实物模型一一对应,在这个过程中逐步搭建、完善自己的空间想象能力。在描述晶体结构的同时,还能够帮助学生计算并掌握晶胞中各种微粒的个数,对于接下来晶体的综合计算能够迎刃而解,一举两得、事半功倍。
(2)金属晶体晶胞的数学模型
利用这个思路还可以构建金属晶体晶胞的数学模型,便于进行晶体的综合计算:
①简单立方(以Po为例):8×=1
②体心立方(以Na为例):8×+1=2
③面心立方(以Cu为例):8×+6×=4
④六方最密(以Mg为例):4×+4×+1=3
(3)分子晶体晶胞的数学模型
分子晶体晶胞的数学模型无需构建新模型,这是由于分子间以范德华力结合的干冰的模型可以视作(8×+6×=4)的面心立方模型;分子间以氢键结合的冰的模型(见图7)与ZnS的模型类似,只不过在这个模型中所有的点都是相同的微粒,故冰的晶体结构数字模型可以表述为8×+6×+4×1=8)。
(4)原子晶体晶胞的数学模型
2013年高考理综新课标1卷中考查了金刚石晶胞的识记,金刚石的晶胞与冰的晶胞类似(见图7),都可以在ZnS的晶胞基础上用数字模型表述为(8×+6×+4×1=8)。可见,以ZnS为基础可以拓展出冰、金刚石等较复杂晶胞的结构,一举三得,这也是前文笔者提到的教师在教学时需要补充ZnS的晶胞的原因所在。
四、学科交叉难点突破
晶胞综合计算中经常用到数学的知识,教师在教学中不能先入为主地认为需用的数学知识学生能够信手拈来,而要提示给他们一些必要的计算公式,比如球体积的计算公式(v=πr3)、立方体面对角线(a)与棱长(l)的关系(a=l)、立方体体对角线(b)与棱长(l)的关系(b=l)。
另外,在教学中使用一些数学用语能够简洁、明确地完成表述。比如确定金刚石晶胞中四个内部点的位置的是学生学习的重点与难点,如果把这个立方体晶胞分为上下两层8个完全相同的小立方体,则四个内部点可以视为上层1、3象限的两个小立方体的体心,下层2、4象限的两个小立方体的体心(见图8)。如此也就不难计算出金刚石晶体中两个碳原子之间最短的距离为/4l(l为晶胞棱长)
区别于之前学习晶体结构时按照课本晶胞结构图形一步到位的看图说话,学生通过分步建模经历由实物模型到数学模型的过程,进而完成了对平面晶胞结构图形理解(见图9),实现了由具体到抽象到运用的思维过程,极大的化解了此部分的难度,可以帮助学生顺利完成此部分内容的学习。
总之,晶体的结构与性质无论对于教师的教学还是学生的学习而言,都是十分具有挑战性的内容。如何帮助学生顺利地掌握这些知识,教师必须用心思考。构建模型作为一种有效的学习方法,在晶体结构的学习中十分重要且有效,另外,建模过程中学生体会到的学习的乐趣以及获得的科学素养的提升也许才是更重要且必要的。
参考文献
[1] 王伟.高中化学“晶体结构与性质”难点测查及其对策研究[D].武汉:华中师范大学,2014,5:27
[2] 薛勇军.高中化学中开展模型教学的研究与实践[D].苏州:苏州大学,2013:11
[3] 沈文选,杨清桃.数学建模导引[M].哈尔滨:哈尔滨工业大学出版社,2008,1:3

