如此解题，我有“异”见

彭小永

[摘 要] 没有研究就没有好的教学，好的解法会令学生终生难忘，但如果我们教师不小心将一些错误解法作为完美的数学模型传授给学生，却可能给学生的终身发展带来极大障碍. 本文在分析两种典型的错误解法的基础上，提出了两个可供大家参考的建议.

[关键词] 创新；核心素养；最短路径；勾股定理

“十三五”规划提出了教育要坚持优先发展、育人为本、改革创新的思想. 作为掌握着祖国未来命运且战斗在一线的人民教师，应该严格奉行陶行知先生“千教万教教人求真”的理念，在《全日制义务教育数学课程标准》（2011版）（以下简称《新课标》）的指引下，坚持“有效地改进教与学的方式，使学生乐意并有可能投入到现实的、有探索性的数学活动中去”的方针，以提高全民的核心素养为使命，积极投身教育教学改革，使人人都能获得良好的数学教育.

在参加骨干教师脱产国培期间，笔者介绍了学生在数学作业中经常犯的两个错误，结果引起一阵骚动，因为很多数学教师在此之前都没有对这两个错误结论做过深入研究，长期按照错误的方法对学生的作业进行批改，学生对此却深信不疑，并把它当作最好的数学模型加以广泛运用. 因此，笔者认为很有必要与大家进行分享.

关于求解最短距离的问题

1. 距离之和最短的问题

在学习“两点之间线段最短”这部分内容时，经常会遇到这样一类问题：

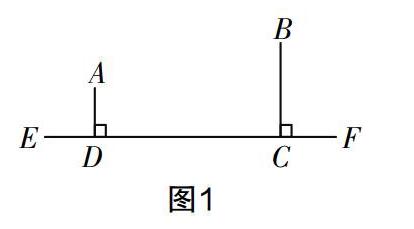
例1：A，B两村在公路EF的同侧，A村离公路的距离AD为1千米，B村离公路的距离BC为2千米，C，D之间的距离为4千米. 如图1，现要在公路边修建一个仓库P，使它到A，B两村的距离之和最小.

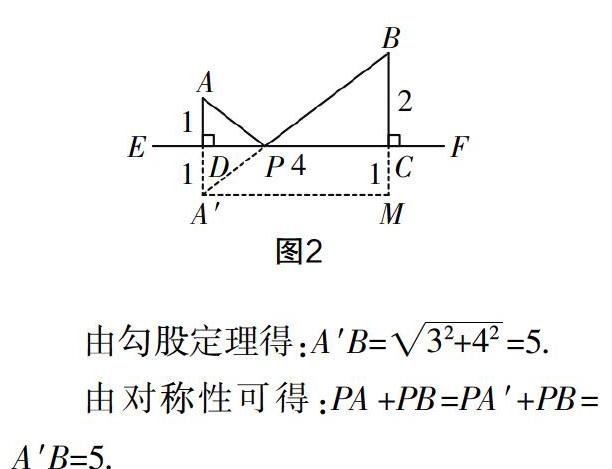
解答这类题时，我们常常作A点关于EF的对称点A′，再作A′M∥EF，交BC的延长线于点M，如图2.

由勾股定理得：A′B==5.

由对称性可得：PA+PB=PA′+PB=A′B=5.

结论是：将仓库建在点P处，它到两个村庄的距离之和最小.

（备注：如果作点B关于EF的对称点B′，可得到同一个P点）

发现这种解答方法后，很多教师便将“作对称点”作为一种经典的数学模型灌输给学生，学生在求解“最短路径”这类问题时，生搬硬套，造成失误而不自知.

2. 最短路径问题

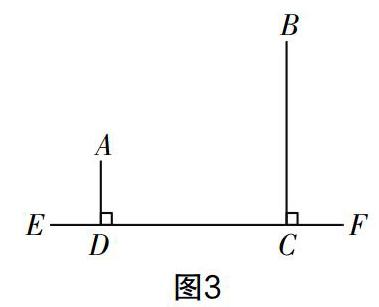
例2：如图3，A，B两个村庄离公路EF的距离AD与BC分别为1千米和3千米，CD=3千米. 现要在河岸EF边建一个水厂向两村输送自来水，铺设水管所需的费用为每千米20000元. （1）请在EF上选择水厂的位置，使得铺设水管所需费用最省；（2）铺设水管的最低费用是多少？

在解答这类习题时，很多人按照例1的解答方式：

如图4，由勾股定理得：A′B==5.

由对称性可得：PA+PB=PA′+PB=A′B=5.

最后得出此题的结论是：将水厂建在点P处时，所需铺设水管的费用最少，为100000元.

不仅有很多同学这样解答，而且很多知名的解题网站提供的解答方法也是如此，很多数学教师也没有发现问题.

其实，这一结论是错误的，我们不妨做如下探讨：

如图5，若水管为DA和AB，过点A作AN⊥BC于N，由勾股定理得：AB==.

因此，水管长度为（+1）千米，这个长度比5千米短，更节省费用.

3. 错因分析及对策

究其例2解答错误的原因，主要是照搬例1的解法，而没有注意到例1中有“使它到A，B两村的距离之和最小”的语句，而例2实际上只需求出“最短路径”就行了，两者存在重大差距.

也就是说，大家今后遇到这类问题，不能生搬硬套资料上或课堂上教师讲解的方法，而应该首先审清题意，再确定合理的解题方法. 对例2这种只需求出最短路径的题型，上述两种情况都应考虑，得出具体数据后，再进行比较才能得出结论.

关于蚂蚁怎样走最近的问题

1. 教材引例

“北师大版《义务教育课程标准实验教科书·数学》八年级上册”第13页的引例：

例3：如图6，有一个圆柱，它的高等于12 cm，底面圆的周长为18 cm，在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面与点A相对的B处的食物，沿圆柱侧面爬行的最短路程是多少？

这个问题的解答，通常是把圆柱沿着它的一条母线剪开，展开成一个长方形，如图7，从而把曲面上的路线问题转化为平面上A，B两点间最短距离问题. 由勾股定理，很容易得出蚂蚁沿着圆柱侧面爬行的最短距离为15 cm.

有了这个例3的示范，很多学生（包括部分教师）根本不管题目的描述是否有变化，都将上述解法作为唯一模式而广泛应用.

2. 变化后的习题

很多习题删掉了“沿圆柱侧面爬行”这几个最关键的字，那结果还会一样吗？

例4：如图8，有一个圆柱，它的高等于4 cm，底面半径为5 cm，在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面与点A相对的B处的食物，蚂蚁爬行的最短路程是多少？

按例3的思路，我们很容易得出蚂蚁从侧面爬行的最短距离为：

≈16.2（cm）.

但如果蚂蚁按A—C—B的路线爬行，只需要爬行4+2×5=14（cm），这个爬行距离小于从侧面爬行的距离.

所以，在习题中如果没有指明爬行的方法，例4的两种算法都有必要，在计算出结果后，通过比较才能得出正确答案.

3. 爬行方法的探讨

如图9，若一个圆柱的底面半径为r，高度为h，一只蚂蚁从点A到点B，到底是选择沿侧面爬行，还是沿着A—C—B爬行才是最短距离呢？

我们不妨假设两条路线的距离相等，找出它的临界点：

即=2r+h.

两边平方得：π2r2+h2=4r2+4rh+h2.

整理得：=≈.

也就是说，圆柱的半径与高度之比略为2 ∶ 3时为临界点（具体比例如上）. 若圆柱的半径与高度之比大于这个临界值时，从直观上看，这时的圆柱为矮胖型的，按图中A—C—B的路线爬行的距离更短；反之，若圆柱的半径与高度之比小于这个临界值时，从直观上看，这时的圆柱为瘦长型的，沿圆柱侧面爬行的距离更短.

在具体解题时，有时还要分析空心与实心、内外表面等情境；在解答长方体的表面两点间的最短距离时，还要考虑多种展开方式，再通过计算与对比分析，才能得出正确的结论. 作为学生，要有认真审题的习惯，要有不唯书、不唯上的批判精神.同时，要学会从数学的角度发现问题和提出问题，综合运用数学知识解决简单的实际问题，增强应用意识，提高实践能力.

两点建议

1. 给教师的建议

没有研究就没有好的教学，创新是引领发展的第一动力. 在我们的日常教学中，我们只有努力成为一个研究型教师，用严谨的态度治学，认真深入地钻研教材，防止在讲解中出现知识性错误，而给学生的终生发展带来障碍.同时，教师应积极营造研究的氛围，合理地使用教材，创新地使用班级的优秀资源，如让学生当小老师等，让他们在课堂内外充分阐述自己的观点和看法，让更多学生体验解决问题的方法的多样性，发展全体学生的创新意识. “授人以鱼，不如授人以渔”，我们教师的主要任务应该是教会他们怎样学，并尽量让他们掌握一些分析问题和解决问题的方法，提升其核心素养和竞争力.

2. 给教材编写者的建议

《新课标》提出：在整个数学教育的过程中都应该培养学生的应用意识，综合实践活动是培养应用意识很好的载体. 由于一些知识性错误有可能给孩子的终生发展带来巨大的影响，所以建议教材的编写者应尽量收集这方面的素材，将“蚂蚁怎样走最近”等内容纳入“综合与实践课”的范畴，或通过在教参中设置多个例题，提示教师引导学生去探讨与分析. 通过师生互动学习，达到教学相长的目的.