建筑结构优化设计理论概述

张巍瀛　张大伟

摘 要：结构优化设计是指将结构分析和最优化原理加以综合，其过程大致是假设-分析-搜索-最优设计。搜索过程即进行修改设计的过程，这种修改不同于过去设计者所采取的经验判断修正，代之以一定的优化方法使设计方案达到“最优”，这一过程是一种主动的、有规划的搜索过程，并以得到最优目标为满足。

关键词：建筑结构；优化设计；变量

一、结构优化设计的基本概念

人们作任何工作时，总希望所选用的所有可行方案中的最优方案。例如：在结构设计中，总是希望在满足结构强度和刚度等约束条件下，希望选择重量最轻，工程造价最低，但实用价值最高的结构形式；另外，在自动控制、农业、林业、商业等方方面面也都存在着大量的寻求最优结果的问题。

二、结构优化设计的层次

工程结构优化设计按照难易程度的层次分为：截面 （尺寸）优化、形状优化、拓扑优化、布局优化、选型优化和系统优化。

1.截面（尺寸）优化：在给定结构的功能、选型、拓扑、材料、形状的情况下，求出满足约束条件的最优截面尺寸，也成为狭义结构优化设计。

2.形状优化：让结构的儿何形状也参与优化，其目的是寻求目标函数最小的结构外形和各单元尺寸。

3.拓扑优化：不仅要解决尺习优化问题，还要确定各节点杆件间的连接方式，是结构领域中更为困难、根抓挑战性的课题。

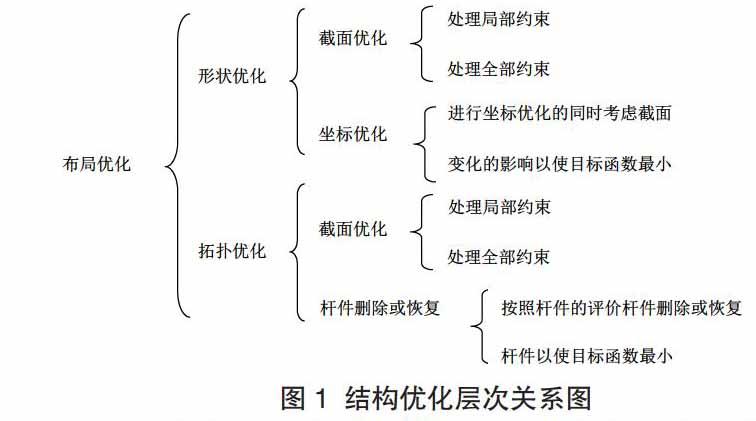
4.布局优化：将结构拓扑、形状和截面相互制约的三个层次的优化综合起来考虑，目的是求得最佳的拓扑、形状和截面分布，其余拓扑、形状、截面优化及约束间的关系如图：

5.选型优化：结构选型是一个综合性很强的问题，它要求力学、结构、建筑学、美术、经济学等诸多学科的密切配合，是对结构功能、社会效益、结构可靠度和造价有重大影响的决策，但目前国内外对其理论尚未进行充分研究。

6.系统优化：也成为全寿命优化，是一个多目标优化问题，包括：经济效益、社会效益、施工及使用期间的安全、使用功能、美学功能和施工方便等要求，其目标是使结构在具有良好功能的前提下，获得更好的整体性和长远的经济效益。

二、结构优化的数学模型

结构优化设计一般的数学模型如下：

求X，使F（x）→min，且满足约束条件：

设满足约束条件的设计点集合为 R 则优化问题的数学模型可简炼地写成求 x 使。从式（1）中可以看出，结构设计的三人要素：设计变量，目标函数、约束条件。

1.设计变量。在优化设计中，需要在优化过程中不断进行修改调整一直处于变化状态的基本参数称为设计变量，又叫优化参数。在对测风塔架进行优化结构设计时，以目前通常采用的桁架式钢结构为例描述其结构特点的参数主要有塔高、塔顶直径、塔底直径、各分段直径以及所选材料等。

设计变量的全体实际上是一组变量，可以用一个列向量表示：

X1 X2 X3……Xn 称作设计变量向量，由n个设计变量所组成的实空间成为设计空间。

2.目标函数。优化设计的目的就是设计出最优的结构。评价一个结构方案的优劣，必须有一个评价设计方案优劣的函数，成为目标函数，目标函数是设计函数的变量，是对设计方案进行比较的指标，是判断设计方案优劣的标准，随着问题的不同，优化设计的目标函数也就不同。航空器设计中，往往选择重量为目标函数，而机械设计中。一般选择以应力集中为目标函数，土建结构设计中的日标函数一般选择建筑成本。很多过程优化设计是在满足所有约束条件的前提下，通过降低结构的重量，来实现建筑成本的降低，例如在钢结构设计中，结构重量越轻，单位面积用钢量越少，自然过程造价也就越低。还有一些实际问题，需要同时实现几个目标的优化，这类为问题成为多目标优化。

通常优化问题要求目标函数最小，即，而有些优化问题则要求目标函数取最大，这是则可通过数学转换规定为目标函数。

本文对测风塔钢结构塔架进行优化的目的在于在满足性能要求的前提下使塔架重量最小即以塔架质量为目标函数。

3.约束条件。设计空间是所有设计方案的集合，但是这些设计方案有些是工程上所不能接受的，如面积质量为取负值，等一个可行的设计必须满足某些设计限制条件，这些限制条件称作约束条件，简称约束。在工程问题中根据约束的性质可以把它们区分为性能约束和侧面约束两大类。针对性能要求提出的限制条件称作性能约束，本文中如塔架结构必须满足强度固有频率范围稳定性及疲劳等性能的要求，不是针对性能要求，只是对设计变量加以限制的约束称为侧面约束。

4.变量连接。由于结构、工艺的原因要求结构的若干各单元取同一设计变量的情况成为变量连接。例如在结构分析中，为了得到较高的精度须将钢板划分为若干各单元进行计算，但山于结构工艺的要求，必须保证整体铡板选取同一规格，结构经过变量连接后，使得优化设计的变量大为减少，往往少于结构的单元数，变量连接设计是相当于在结构各截的面设计变量间增加了一些等式约束。

5.基本假定。进行结构截面优化设计时，通常采用以下假定：（1）一 轮优化设计中，各单元内力不随设计变量的变化而变化；（2）在一轮优化设计中，结构的各阶振型不随设计变量的变化而变化；（3）在一轮优化设计中，结构的失稳波形不随设计变量的变化而变化；（4）一组杆件截面面积的增加使真个结构的位移减小，反之则增大；（5）一组杆件截面面积的增加使真个结构的固有频率增加，反之则减小；（6）一组杆件截面面积的增加使真个结构的稳定性系数增加，反之则减小；

参考文献：

[1] 钱令希.工程结构优化设计，水利电力出版社，1983.

[2] 张向庭.结构风压与风振计算，同济大学出版社，1985.