“动手做”课堂样式新探索
芮金芳
[摘 要]
“动手做”作为新教材组成的重要因子,在课堂教学中发挥着特殊的教育价值功能。教给学生“动手做”这一解决问题的基本策略,并使学生以“他人引导”逐步走向“自主需要”,培养学生的创新能力,提高教学的有效性。
[关键词]
“动手做”专题;价值厘定;实践策略
苏教版新修订教材自一年级开始,教材新增设置“动手做”栏目,意在培养学生动手实践能力,指向学生在数学活动中数学活动经验的积累。基于数学活动经验的“数学”本质和“经验”属性,“动手做”旨在强调学生边做边思考,着力于引导学生在活动中深化对数学知识和探究问题方法的理解,组织对活动过程进行反思和交流,同时,“动手做”还精选具有数学文化底蕴的素材作为活动载体,让学生在“做”的过程中体验数学文化的魅力。
一、“动手做”的类型
笔者梳理教材中“动手做”编排序列,每册教材中至少安排2-3个“动手做”活动主题,有的是对所学内容的丰富拓展,有的是对数学应用价值的补充说明,有的是基于数学思维的延展生长……根据其内容呈现和所承载的育人价值功能,大致分为以下几种类型。
(一)操作设计类
根据教材中所学内容,在后续部分出现与之相配套的“动手做”环节。主要利用学生已有的知识经验,展开动手操作,观察交流等活动。操作的过程不仅有利于培养学生动眼观察和动手操作的能力,还有利于培养学生动嘴表达和动脑思考的能力。比如在初步认识长、正方形、三角形、圆形后进行图案的剪拼交流活动;在认识轴对称图形后进行图形对称设计活动;在认识平移旋转后开展风车制作活动;认识方向后制作方向板等。
(二)生活应用类
数学与生活密切联系,数学来源于生活,又高于生活。“动手做”中部分主题取自丰富多样的生活场景,引导学生学会用数学的眼光留心观察身边的生活现象,关注源自生活实践的真实问题,提升学生的综合学科素养。比如认识时分秒后制作圆盘记录不同时刻太阳的影子位置,留心身边的时间问题;认识分米和毫米后,记录大蒜不同时期的生长高度,发现生活中的数学现象;认识升和毫升后,制作1升的量器,估计生活中不同容器的容量。
(三)游艺体验类
学与玩的有机融合,让儿童在回归玩的天性中收获对数学新的认识和体验。在玩中学,在学中玩符合儿童数学认知的一般规律。可以结合对应数学内容开发相应“玩中学”的数学课程,学生在活动中体验,在玩中发展数学思维,体会数学基本思想和思维方式,彰显数学智慧。如认识三角尺后,举行一副三角尺的拼摆数学游戏活动;在认识图形旋转后,利用旋转将喜羊羊拼图恢复原位游戏活动;认识可能性后,举行摸球游戏活动,体验感受事件发生的可能性。
(四)实验探究类
“动手做”中有很多富有探究意味的数学实验,引领学生充分经历发现问题、提出问题——设计实验步骤——分享实验成果——自我反思评价的“做数学”过程,在这样的学习中,至始至终有思维的介入,理解能力、交流能力、收集处理信息能力等共同作用,有效促进学生数学素养的综合提升。如滴水实验,通过亲历实验过程,获得1元硬币上水滴的有效数据;图形分割实验,根据小图形要求将正方形、长方形进行合理、正确分割,感受图形排列特征及个数间的规律;分数墙实验活动,让学生体会不同分数之间的内在关联。
“动手做”作为苏教版数学教材中新设的专题板块,如何进行这类专题的教学呢?以三年级下册“年月日”单元中的“动手做”为例,它是在学生初步掌握年月日基本知识后,安排的一次在月历表中探寻规律的专题活动。利用两次框数活动,让学生初步体会月历表中框3个数的和与3个数之间的联系,由此引发到框4个数求和规律的探究,最后引申到框若干个数(如5个、6个、7个、8个等)规律本质的揭示。
鉴于以上对教材内容的初步分析,从学生的视角出发,我们认为,本次“动手做”专题活动可以归属于实验探究类型。波利亚曾说过:让我们教猜想吧!可以以“猜想”为主要学习线索,让学生经历“直觉、猜想——尝试、推测——出错、求证——推理、联想”开启学生的一次实验探索之旅。
二、“动手做”教学实施策略
(一)直觉引领,诱发疑问
数学直觉思维是人们对数学对象、结构及关系的直接洞察和直观领悟,它是数学发现、发明的重要起始节点。很多大的数学猜想、发现往往都是从直觉开始的。
学生要对研究素材产生直觉,必须首先激发他们关注的兴趣点。正如波利亚所说:“为了有效地学习,学生应当对所学习的材料感兴趣并在学习活动中找到乐趣,这是最佳动机。”
在“月历表中的有趣规律”课始,呈现一张月历表,让学生在月历表中任意选择三个连续的数,快速报出日期,教师能又快又准地说出它们的和。几轮下来,老师都没有出现错误,学生非常诧异,心生疑惑:老师能算得这么快,这里面一定隐藏着什么秘密,有什么规律呢?教师此时引导学生仔细观察月历表,根据月历表中数的排列,你有什么发现?
发现1:横排每相邻的两个数都相差1。
发现2:竖排每相邻的两个数都相差7。
发现3:斜排(从左上到右下)每相邻两个数都相差8。
发现4:斜排(从右上到左下)每相邻两个数都相差6。
……
利用学生喜闻乐见的游戏情境一下吸引学生的关注点,同时激发他们进一步深入探究规律的欲望。获胜的秘诀到底在哪里?引导学生仔细观察月历表中数的一般排列规律,产生了零星的直觉感悟,为后面继续深入探究埋下了种子。可见,一个引人入胜的情境是数学猜想开始的重要起点。
(二)尝试探究,类比推理
任何直觉的顿悟都离不开实验的求证。我们做了,才知道事实的真相是怎样。所以教师适时提供动手操作的学具,目的是给学生提供直观的支撑,让学生在“做数学”活动过程中,对探究的规律形成一种新的结构化的认识。
1.小组进行第一次框数游戏活动。
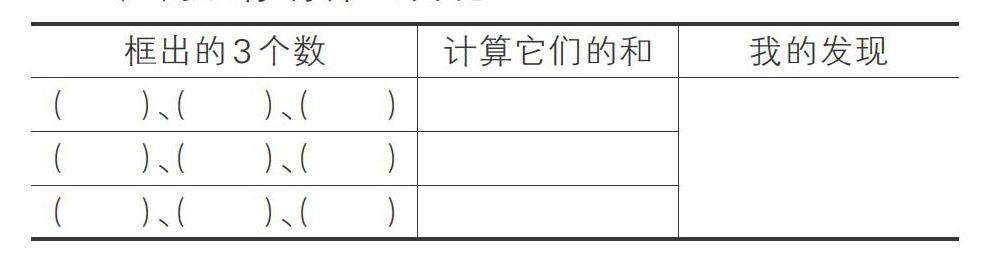
框数游戏:研究每次框3个数的规律。
(1)框:每次框3个数;
(2)说:这3个数之间的关系;
(3)算:算出它们的和;
(4)找:你有什么发现?
2.汇报交流:横着框3个数,3个数的和与中间数有关;
竖着框3个数,3个数的和与中间数有关;
斜着框3个数,3个数的和与中间数有关;
3.概括规律:每次框出3个数,不管框的位置怎样,3个数的和都可以用“中间数×3”快速计算。
4.验证规律:小组内框出3个数检验规律。现在你知道老师为什么算得快的秘密吗?
学生在小组合作探究中逐步完善“每次框3个数”求和的方法,通过动手框一框、算一算、想一想、比一比等活动让学生每次框出不同的3个数,既丰富学生对规律的初步感知,又积累了丰富的研究素材。引导学生比较反思、回顾中,将探究活动得到的初步体验进一步提升,从而抽象概括出“每次框3个数求和”的本质规律特征,为后面进一步深入探究其他情况,提供了很好的研究范式。
(三)大胆推测,出错求证
在探究规律中,学生常常陷入规律总是正确的窠臼中,每次探究的经历总是一帆风顺,这容易让学生的思维陷入平铺直叙的低水平阶段。因此,在本节课的后半段教学进程中,教师故意打破现成规律,让学生在一波三折中感受规律的获得不(下转第25页)(上接第19页)一定是一步到位,可能会一错再错,需要在不断的举例求证中纠错、明晰、完善、再建立。
小组进行第二次框数游戏活动。
质疑:刚才发现3个数求和的规律还适用求4个数的和吗?(大部分学生赞成)
框数游戏:研究每次框4个数的规律。
(1)框:每次框4个数;
(2)说:这4个数之间的关系;
(3)算:算出它们的和;
(4)找:你有什么发现?
汇报交流:横着框4个数,4个数的和与中间两个数的和有关;
竖着框4个数,4个数的和与中间两个数的和有关;
两行、两列框4个数,4个数的和与对角线上两个数的和有关;
完善规律:每次框出4个数,4个数的和可以用“中间两个数的和×2”快速计算。
验证规律:小组内框出4个数检验规律。
在探索每次框3个数的基础上,充分利用已有的探索活动经验,继续深入探究每次框4个数中的规律,不仅实现知识的融合,更渗透方法的迁移、活动经验的累积运用,体会数学化归思想,实现一类相似结构数学问题的研究模式。学生在一开始的确信框4个数的规律和3个数相同,到后面实验操作后的调整、反思、明了,恰恰是学生思维从原先的单一、固化、线性走向多元、灵活、发散的生长过程,让学生在曲折变化中获得敏锐的发现、深刻的理解。
[参 考 文 献]
[1]郑毓信.数学思维与小学数学[M].南京:江苏教育出版社,2008.
[2]顾泠沅.数学课堂教学研究[M].上海:上海教育出版社,2010.
(责任编辑:张华伟)

