一种快速寻找最短路径的算法
朱世宇 张洪明
摘要:最短路径算法是计算机科学与地理信息科学等领域的研究热点。从工业机械运动到城市道路网络,最短路径算法是其中不可或缺的一部分。最短路径问题是图论研究中的一个经典算法问题,旨在寻找由结点和路径组成的图中两结点之间的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。本文介绍了一种以最邻算法为基础进行改进的算法。
关键词:最短路径 算法 图论
中图分类号:TP301 文献标识码:A 文章编号:1007-9416(2016)07-0115-02
1 引言
最短路径算法是计算机科学与地理信息科学等领域的研究热点。从工业机械运动到城市道路网络,最短路径算法是其中不可或缺的一部分。本文以试验坐标点为例子讨论了采用最短路径算法的优势,并提出了一种快速寻找最短路径的算法。在很多文献中,研究人员已提出过多种关于路径优化的问题的求解算法[1~4]。本文在综合最优路径的算法研究上主要提出了1种基于最邻算法的改进算法。
2 区域最邻算法
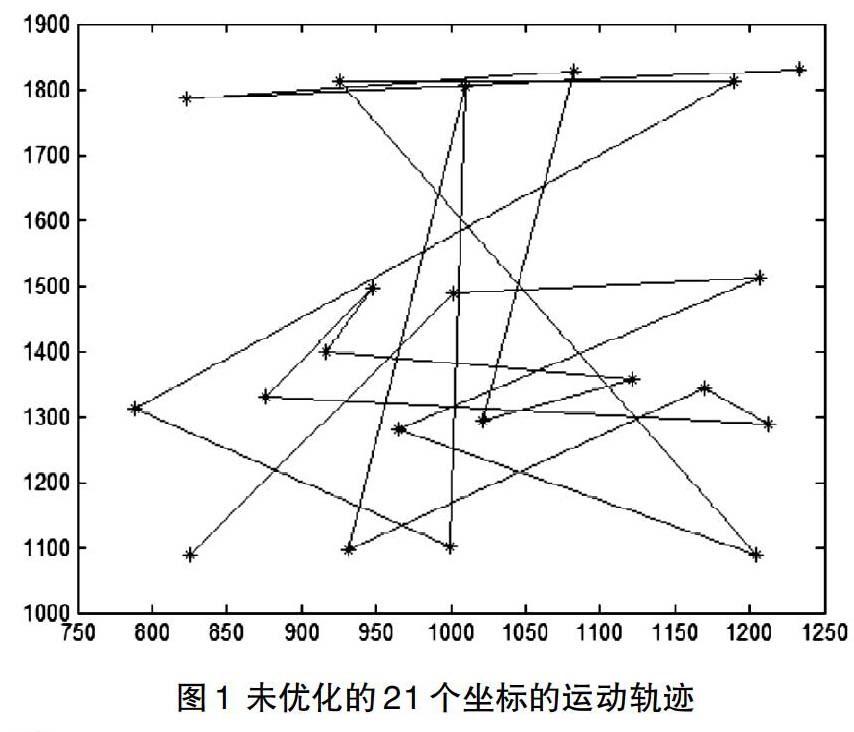
以表1所示的坐标进行试验,在未进行优化的时候,按其原有的排列顺序进行移动,其运动轨迹如图1所示,以试验坐标点为单位,从第一个点到最后一个点运动路程共7252.39。
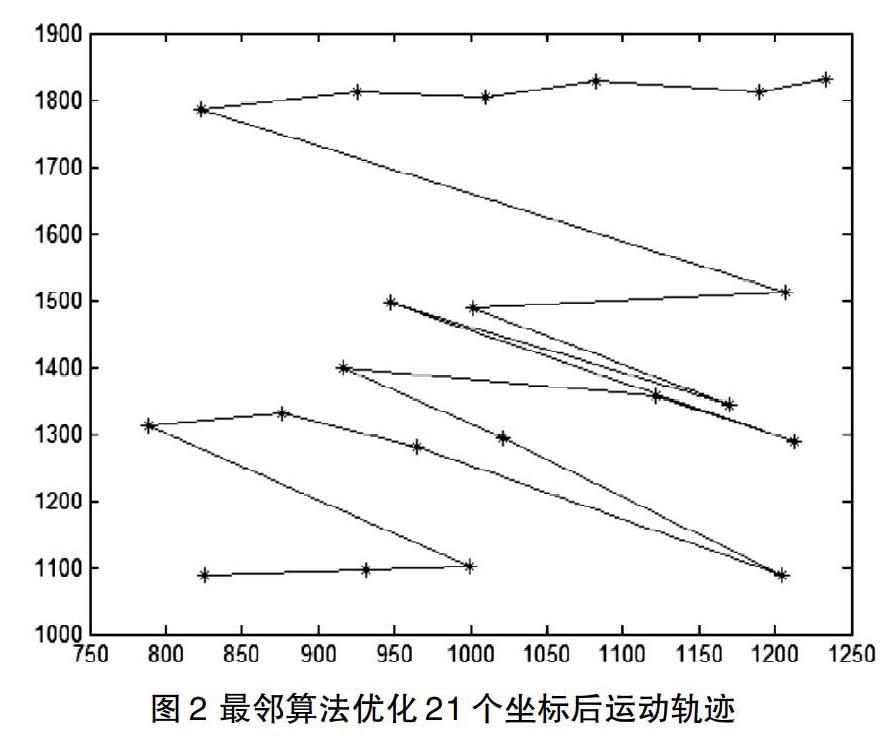
从图1可以看出,未对坐标进行优化之前,运动轨迹非常的混乱。使用最邻算法对表1坐标进行排序后,得到表2,按其排列顺序进行移动,其运动轨迹如图2所示,以坐标为单位,从第一个点到最后一个点运动路程共3642.559。
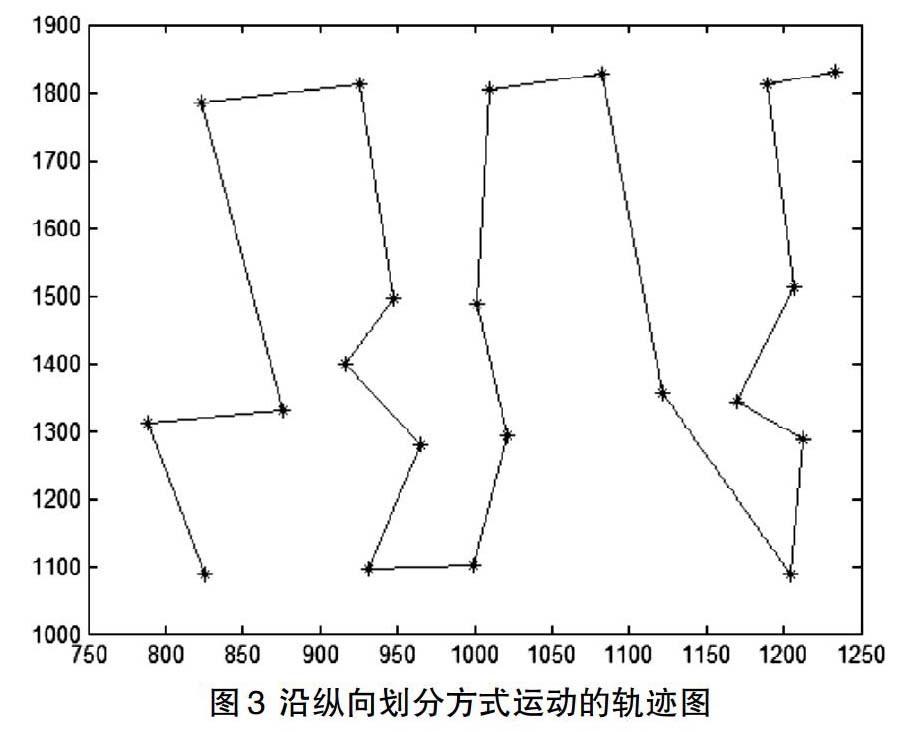
图2的移动的路径较之前的运行轨迹更加合理[5],但是经过研究其实还有提升的空间。本文在最近邻方法上,进行了改进,使用了一种区域划分的方式将整个打坐标分布的区域划分别划分为横纵的5行。如果是以纵向的宽度划分区域的话,那么从第一行起,坐标的排列顺序为横向从小到大排列,而第二行则是从大到小,第三行再从小到大,以此类推。而如果是以横向划分区域,则是以纵向进行大小排列。以纵向划分方式对表1中的坐标排序后,得到表3,按其排列顺序进行移动,其运动轨迹如图3所示,以坐标为单位,从第一个点到最后一个点运动路程共4004.745。
3 结语
以试验坐标为例,优化后的机械手移动路径比未经优化的路径节约路程7252.39-2324.798=4927.59,节省了约原来一半多的的路程。
参考文献
[1]Wu C G, Liang Y C , Lee H P , et al. Generalized chromosome genetic algorithm for generalized traveling salesman problems and its applications for machining[J]. Physical Review E , 2004 , 70(1):1~13.
[2]Dimitrijevic V , Saric Z. Efficient transformation of the generalized traveling salesman problem into the traveling salesman.problem on digraphs[J].Information Sciences,1997,102(1~4):105~110.
[3]Lien Y N , Ma E , Wah Benjamin W S. Transformation of the generalized trav-eling-salesman an problem into the standard trav2eling2salesman problem[J].Information Sciences,1993,74(1~2):177~189.
[4]Tsai I C F , Tsai C W, Tseng C C. A new hybrid heuristic approach for solving large traveling salesman problem[J].Infor2 mation Sciences,2004,166(1~4):67~81.
[5]赵赫,杜端甫.TSP的邻域搜索算法的分析和改进[J].中国管理科,1997,5(1):35~39.

