基于MATLAB的众筹筑屋规划方案的核算程序实现

摘要：针对2015年全国大学生数学建模竞赛题D题：众筹筑屋规划方案设计问题，在文中建立了规划方案的核算与优化模型。本文重点说明通过编辑MATLAB程序，对复杂的核算问题进行计算，从而得出相关的核算数据，使用该程序核算非常方便，可推广到其他有关增值税的核算问题中。

关键词：众筹筑屋 方案 核算 程序

中图分类号：TU12 文献标识码：A 文章编号：1007-9416（2016）07-0068-02

2015年全国大学生数学建模竞赛题D题：众筹筑屋规划方案设计。在文中建立了众筹筑屋规划方案的核算与优化模型，本文通过编辑MATLAB核算模型程序，对规划方案Ⅰ、改进方案Ⅱ和优化方案Ⅲ进行全面核算。

1 众筹筑屋规划方案的MATLAB核算程序

%计算每种房型的建筑面积d，开发成本C，售房收入R，各项成本XC，容积率r，增值税Z，纯利润L，投资回报率ROI，%b是各种房型的建筑套数

function [d，R，r，XC，Z，L，ROI]=hesuan（b）

a=[77，98，117，145，156，167，178，126，103，129，133]； %每种房型的面积

c=[4263，4323，4532，5288，5268，5533，5685，4323，2663，2791，2982]；%每种房型的开发成本

p=100*[120，108，112，128，128，136，140，104，64，68，72]； %每种房型的售价

d=a.*b；%每种房型的总面积

C=c.*d；%每种房型的开发总成本

R=p.*d；%每种房型的总收入

r=sum（d（1：8））/102077.6；%容积率

d1=[d（1：8），d（11）]；%提取房型1-8、11的面积

alf=sum（d1（1：3））/sum（d1（4：9））；%普通宅与非普通宅的面积之比

f=[C（9）；C（10）]*[alf/（1+alf），1/（1+alf）]；%将房型9、10的开发成本按比例分摊为普通宅与非普通宅

g=[R（9）；R（10）]*[alf/（1+alf），1/（1+alf）]；%将房型9、10的收入按比例分摊为普通宅与非普通宅

f=round（f）；g=round（g）；

%计算每种房型的五种扣除项目金额

CF1=[C（1：2），0，C（4：7），0，f（1，：），f（2，：），0]；%房型3、8、11的开发成本不允许扣除记为0，房型9、10按分摊计

CF=[C（1：8），f（1，：），f（2，：），C（11）]； %各种房型的开发成本，房型9、10按分摊计

RF=[R（1：8），g（1，：），g（2，：），R（11）]；%各种房型的收入，房型9、10按分摊计

dF=[d（1：8），d（9），0，d（10），0，d（11）]；

w=777179627；

s=w/sum（d）；%每单位建筑面积分摊的土地支付金额

S1=s*dF；%每种房型分摊的土地支付金额

S2=CF1；%房型3、8、11的开发成本不允许扣除

S3=（S1+S2）*0.1；%每种房型的开发费用

S4=RF*0.0565；%每种房型与转让房地产有关的税金

S5=（S1+S2）*0.2；%每种房型的其他扣除项目

S=S1+S2+S3+S4+S5；%每种房型总的扣除金额

bet=RF./S；%每种房型的收入与扣除项目金额之比

S=round（S）；

%以下计算增值税

X=zeros（1，13）；

for i=1：13

if bet（i）>1.5&bet（i）<=2

X（i）=（0.4*bet（i）-0.45）*S（i）；

elseif bet（i）>2&bet（i）<=3

X（i）=（0.5*bet（i）-0.65）*S（i）；

elseif bet（i）>=3

X（i）=（0.6*bet（i）-0.95）*S（i）；

end

end

for i=1：3

if bet（i）<=1.2

X（i）=0； %普通宅当bet《=1.2时免增值税

elseif bet（i）>1.2&bet（i）<=1.5

X（i）=（0.3*bet（i）-0.3）*S（i）；

end

end

for i=4：13

if bet（i）<=1.5

X（i）=（0.3*bet（i）-0.3）*S（i）；

elseif bet（9）<=1.2&bet（11）<=1.2

X（9）=0；X（11）=0； %普通宅当bet《=1.2时免增值税

end

end

Y=round（X）；

Z=[Y（1：8），Y（9）+Y（10），Y（11）+Y（12），Y（13）]；

%计算投资回报率

CB=round（S1+CF+S3+S4）； %成本，其中w=sum（S1），sum（CF）=sum（C）

XC=[CB（1：8），CB（9）+CB（10），CB（11）+CB（12），CB（13）]； %计算房型1-11的各项总成本

L=R-XC-Z；

CC=sum（CB）；

SY=sum（R）； %收益，sum（RF）=sum（R）

ROI=（SY-CC）/CC； %投资回报率

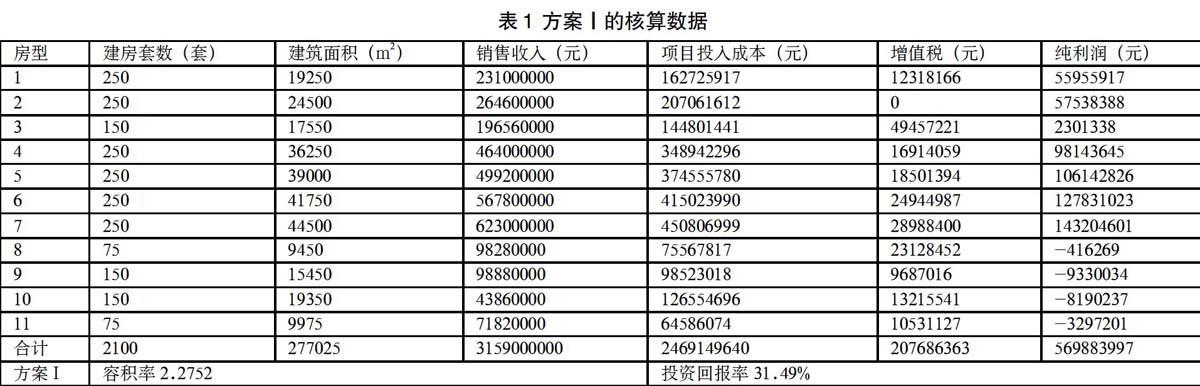
2 众筹筑屋方案Ⅰ的程序核算数据

在MATLAB命令窗口输入方案Ⅰ的建设套数：

b=[250，250，150，250，250，250，250，75，150，150，75]；

[d，R，r，XC，Z，L，ROI]=hesuan（b）

回车，即可得到方案Ⅰ全面核算数据见表1所示。

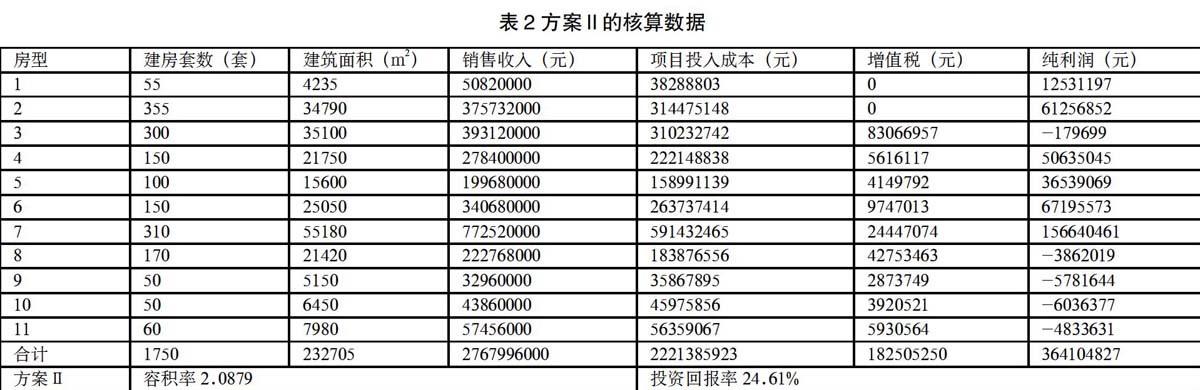
3 改进的方案Ⅱ的程序核算数据

通过对参筹者进行抽样调查，得到了参筹者对11种房型购买意愿的比例，为了尽量满足参筹者的购买意愿，需重新设计建设规划方案（称为方案Ⅱ），并对方案II进行核算。

在MATLAB命令窗口输入方案II的建设套数：

b=[55，355，300，150，100，150，310，170，50，50，60]；

[d，R，r，XC，Z，L，ROI]=hesuan（b）

回车，得到方案II全面核算数据见表2所示。

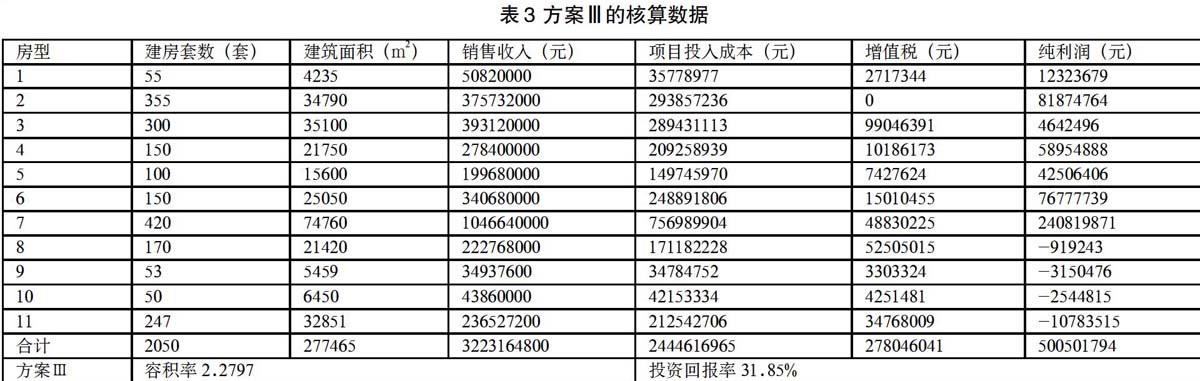
4 优化后的方案Ⅲ的程序核算数据

一般而言，投资回报率达到25%以上的众筹项目才会被成功执行，而方案Ⅱ的投资回报率ROI=24.61% ，需要对方案Ⅱ进行优化改进，使其投资回报率达到25%以上。

在MATLAB命令窗口输入优化后的方案Ⅲ的建设套数：

b=[55，355，300，150，100，150，420，170，50，50，60]；

[d，R，r，XC，Z，L，ROI]=hesuan（b）

回车，得到方案Ⅲ的核算数据见表3所示。

由表1、表2可以看出，优化后的方案Ⅲ比方案Ⅱ投资回报率提高7.24%，建房套数增加300套，纯利润增加136396967元，优化效果显著。方案Ⅲ既考虑投资者的购买意愿，又兼顾了开放商的利益，该方案可成功实施。

5 结语

通过编辑MATLAB核算函数程序，只要输入规划方案的建设套数，就能很方便地核算出重要的相关数据，减少了大量的重复计算。若核算数据未达到要求，可建立优化模型进行改进使其达到预设目标。该方法和程序运用到其他行业的核算中非常简捷方便。

参考文献

[1]吉耀武.众筹筑屋规划设计的核算与优化[J].中小企业管理与科技，2016.2.

[2]中华人民共和国土地增值税暂行条例.中华人民共和国国务院[第538号令].

[3]胡良剑，孙晓君.MATLAB数学实验[M].北京：高等教育出版社，2006.06.

[4]肖华勇.实用数学建模与软件应用[M].西安：西北工业大学出版社，2008.11.