一新型3自由度柔性微动平台的设计和分析
赵鹏 高金海

摘 要:为解决微定位平台大行程与高精度之间的矛盾,本文设计一新型柔性精密微动平台,并利用螺旋理论对其进行相应的运动特性分析。该柔性微动平台是将三个柔支链构分别作用于工作台的三个轴向上,对柔性机构施加相应的力,使工作台做相应的移动。通过对该平台的有限元分析,获取施加力与各个轴向位移的关系,及输入位移与输出位移之间关系,以使该柔性微动平台达到微米级定位精度的目的。
关键词:微动平台;柔性机构;螺旋理论;有限元分析
中图分类号:TH703 文献标识码:A
1 前言
20世纪80年代后期开始,柔性机构被Purdue大学提出,并逐渐引起机械科学家和工程师的重视。它指在外加荷载作用下,通过组成构件间的部分或全部弹性变形实现所需运动和功能的一类机构。与传统刚体机构相比,它不是停留在如何避免杆件的变形,而是积极利用柔性机构的变形来传递力和运动。大大降低了机构重量、简化了制造过程、提高了运动精度且易于微型化等。目前,柔性机构已经被应用于日常生活和有特殊要求的行业上,尤其在集成电路制造和微细加工等宏观及微观领域中有着广泛的应用前景。而微动工作台在精密加工与测量、微电子工程、纳米科学与技术等领域的作用越来越重,具体应用包括:扫描探针显微镜和计量仪、纳米探针扫描、内存存储器、硬盘驱动器及生物成像等设备。
为解决微定位平台大行程与高精度之间的矛盾,本文依据“伪刚体模型”理论设计一新型柔性微动平台,采用螺旋理论分析了所提出的机构末端运动特征,得到了该机构具有3个平移自由度的结论。并采用ANSYS软件对所建模型进行了柔度分析和靈敏度分析,为类似微动平台设计与分析提供思路。
2 设计理论基础
“伪刚体模型”方法由HOWELL最先提出,并对多种基本的柔性单元进行了伪刚体建模,为伪刚体模型法的发展奠定了理论基础。如图1所示,将两根连杆铰接并施加扭簧来模拟悬臂梁的变形,通过获得铰接点位置,以刚性连杆的位移近似逼近柔性梁的变形。这样,柔性杆的运动特性由带有铰链的刚性杆模拟,进而用刚性结构理论知识来解决柔性结构。从图1(b)可得到关系式有:
梁末端坐标lx、ly:
(1)
(2)
伪刚体角θ:
(3)
对于横截面宽为w、高为h的梁,有:
(4)
(5)
式中:γ为特征半径系数,p、np为图示中的作用力。
用伪刚体模型很容易模拟出柔性平行导向机构的轨迹。应用运动学的标准位置分析方法来分析图2(b)所示平行导向机构的伪刚体模型,很容易确定点P的轨迹方程。
P点坐标xp、yp:
xp=γlcosθ+a3 (6)
yp=γlsinθ+l(1-γ)+b3 (7)
伪刚体模型法是一种刚体替换法,通过运动学等效替换,为分析、研究非线性大变形单元提供一种简单有效的方法。而柔性平行导向机构除了保持柔性机构的优点外,还消除铰链摩擦、回差以及不用润滑油。
3 微动平台的设计及分析
3.1 微动平台设计
本文依据伪刚体模型理论及柔性平行导向机构理论,采用柔性板与柔性杆件的特征进行设计,并将三个相同的柔性机构置于微动平台的三个轴向上,以此实现具有3维空间运动平台。通过给定不同轴向力的大小及方向来获取多自由度的运动,本文设计的核心是实现微动平台的多自由度运动。据此所设计的柔性支链与微动平台如图3、图4所示。
为保证柔性机构在失效前能获得更大的变形,选取柔性机构的材料为1060铝合金,其密度为2700kg/m3,弹性模量为71GPa,泊松比为0.33。微动平台的柔性支链如图3所示,其主要设计结构参数见表1。
表1柔性支链结构参数(/mm)
L1 L2 L3 L4 L5
60 40 15 11.5 40
L6 h1 w1 h2 w2
20 1 1 0.5 10
注:h1、w1、h2、w2分别为L5、L6对应的厚度和宽度。
3.2 柔性支链运动特性分析
将柔性支链通过伪刚体模型简化后建立结构简图及坐标系如图5所示。设该位形下球铰中心P12,P13,P14坐标分别为(x1,0,z)、(x1+x2,0,z)、(x2,0,0)。
由螺旋理论可得P11-P12支链的运动螺旋系为:
(8)
由上式可求P11-P12支链的约束反螺旋系为:
S′11=(x10z000) (9)
同理可求的P14-P13支链的约束反螺旋系为:
S′11=(x10z0-x2z0) (10)
由此可得P11-P12-P13-P14封闭子链的运动螺旋系为:
(11)
因为支链模型中还包含一个移动副,所以柔性支链的运动螺旋系为:
(12)
求上式反螺旋可得柔性支链的约束螺旋系为:
S1′=(000010) (13)
从柔性支链的约束螺旋系可知,每个柔性支链对动平台都施加一个转动约束力偶,根据柔性平台模型特性可知,作用在动平台上的3个转动力偶线性无关,因此动平台绕x,y,z轴的转动被约束,平台只剩下沿x,y,z轴的3个移动自由度。即该柔性平台的自由度数为3。
3.3 有限元分析
验证所设计平台的运动性能,采用Ansys有限元分析软件对其分析。材料弹性模量为E=71.7GPa,泊松比v=0.33。为满足求解精度,同时考虑柔性件的厚度较小,采用自由网格划分,如图6所示。
3.3.1 运动性能分析
采用机构输入力与输出位移之间关系来表示微动平台的运动性能。而其输入力和输出位移之间的关系,即微动平台的柔度定义是设计和评价微动平台精度的一项重要指标。采用如下的柔度矩阵表达式分析所设计平台性能。
(14)
式中:Co,FIN为柔度矩阵,Fin为输入端输入力向量,Uout为输出位移。
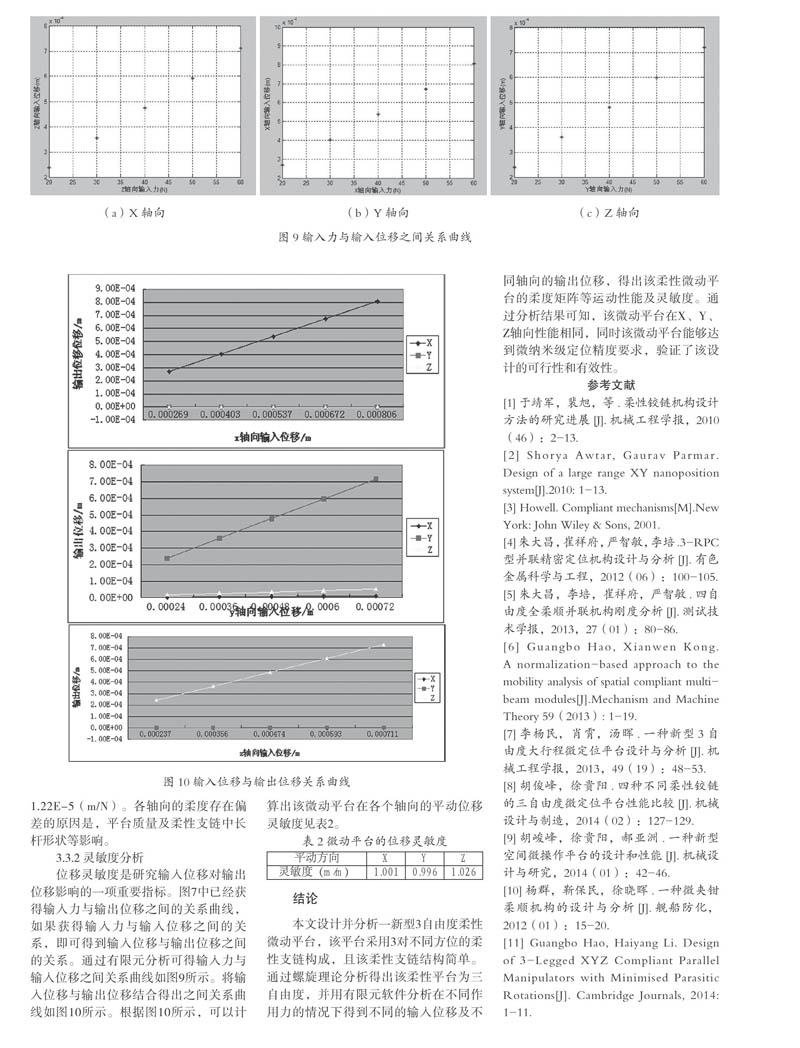
通过Ansys软件分析可得不同方向不同大小作用力的情况下,动平台在各个方向位移分析如图7所示。从图7中可知作用力与位移近似成正比,且满足微纳米精度。Y轴向受40N时,Ansys软件对位移的分析云图如图8所示。期望的运动是沿Y坐标,但发现伴随有X、Z方向的移动,这些伴随运动会很小,其伴随运动位移/主运动位移<5%。且当图3柔性机构中的L5长度越长,其伴随运动位移/主运动位移越小。
将分析结果代入公式(14)可得该平台的柔度矩阵为:
从柔度矩阵可以看出,该微动平台在X、Y、Z轴向的柔度矩阵分别为1.34E-5(m/N)、1.19E-5(m/N)、1.22E-5(m/N)。各轴向的柔度存在偏差的原因是,平台质量及柔性支链中长杆形状等影响。
3.3.2 灵敏度分析
位移灵敏度是研究输入位移对输出位移影响的一项重要指标。图7中已经获得输入力与输出位移之间的关系曲线,如果获得输入力与输入位移之间的关系,即可得到输入位移与输出位移之间的关系。通过有限元分析可得输入力与输入位移之间关系曲线如图9所示。将输入位移与输出位移结合得出之间关系曲线如图10所示。根据图10所示,可以计算出该微动平台在各个轴向的平动位移灵敏度见表2。
表2微动平台的位移灵敏度
平动方向 X Y Z
灵敏度(m/m) 1.001 0.996 1.026
结论
本文设计并分析一新型3自由度柔性微动平台,该平台采用3对不同方位的柔性支链构成,且该柔性支链结构简单。通过螺旋理论分析得出该柔性平台为三自由度,并用有限元软件分析在不同作用力的情况下得到不同的输入位移及不同轴向的输出位移,得出该柔性微动平台的柔度矩阵等运动性能及灵敏度。通过分析结果可知,该微动平台在X、Y、Z轴向性能相同,同时该微动平台能够达到微纳米级定位精度要求,验证了该设计的可行性和有效性。
参考文献
[1]于靖军,裴旭,等.柔性铰链机构设计方法的研究进展[J].机械工程学报,2010(46):2-13.
[2] Shorya Awtar, Gaurav Parmar. Design of a large range XY nanoposition system[J].2010: 1-13.
[3] Howell. Compliant mechanisms[M].New York: John Wiley & Sons, 2001.
[4]朱大昌,崔祥府,严智敏,李培.3-RPC 型并聯精密定位机构设计与分析[J].有色金属科学与工程,2012(06):100-105.
[5]朱大昌,李培,崔祥府,严智敏.四自由度全柔顺并联机构刚度分析[J].测试技术学报,2013,27(01):80-86.
[6] Guangbo Hao, Xianwen Kong.A normalization-based approach to the mobility analysis of spatial compliant multi-beam modules[J].Mechanism and Machine Theory 59(2013): 1-19.
[7]李杨民,肖霄,汤晖.一种新型3自由度大行程微定位平台设计与分析[J].机械工程学报,2013,49(19):48-53.
[8]胡俊峰,徐贵阳.四种不同柔性铰链的三自由度微定位平台性能比较[J].机械设计与制造,2014(02):127-129.
[9]胡峻峰,徐贵阳,郝亚洲.一种新型空间微操作平台的设计和性能[J].机械设计与研究,2014(01):42-46.
[10]杨群,靳保民,徐晓晖.一种微夹钳柔顺机构的设计与分析[J].舰船防化,2012(01):15-20.
[11] Guangbo Hao, Haiyang Li. Design of 3-Legged XYZ Compliant Parallel Manipulators with Minimised Parasitic Rotations[J]. Cambridge Journals, 2014: 1-11.

