学生在中央的数学课堂

张冬梅 江苏省特级教师，中学高级教师，南京师范大学教育硕士生导师，南京师范大学、江苏师范大学“国培计划”专家委员，南京市琅琊路小学教师发展中心主任。曾获全国科研优秀教师、江苏省先进教育工作者、江苏省“226”工程培养对象等称号。多次参加课堂教学评比，获全国小学数学优化课堂教学评比一等奖、全国优秀录像课评比一等奖、江苏省优质课评比一等奖第一名等好成绩。

教学风格以“亲和”为特色，主张“亲和数学亲和学”，既关注数学本身的“亲和”，又强调要“亲和”地学。其领衔的名师工作室致力于“亲和数学”的研究，着力构建数学内涵与儿童趣味相和谐的数学学习活动，既关注数学课堂的“数学味”，又关注儿童的生命价值与生活世界，使儿童获得生命成长。

教学内容：

苏教版数学五年级下册《方程》单元第4课时（练习课），练习内容参考第8～13题。

教学目标：

1.通过分享与练习，使学生进一步理解方程的内涵。

2.进一步掌握等式的性质，能根据等式的性质正确地解方程，并形成相应的技能。

3.在自主学习、合作分享的过程中感受数学的魅力，获得数学学习的方法，提升学生的学习力。

教学准备：

（教师）课件、小黑板；（学生）学习单、错题集等。

课堂实录：

一、简单回顾

师：同学们，这堂课，我们将进行有关“方程”的第一次分享会，回忆一下，我们已经学习了哪些有关方程的知识？

生1：我们学习了什么是等式和什么是方程。（板书：等式和方程）

生2：我们还学习了等式的性质和解方程。（板书：等式的性质和解方程）

二、热情分享

（一）小组交流

师：关于这两项内容，大家有些什么学习体会与经验呢？先请大家在小组内分享，要求（屏幕显示）：

四人小组任选其中一项内容进行组内交流活动。

（二）全班分享

1.分享有关“等式和方程”的相关知识与学习体会

师：哪些小组是选择第一项内容的？选两个代表来跟全班分享。

（一小组的两位同学上讲台前当小老师跟大家分享，全班互动）

小老师1：我们想先举个例子考考大家（边说边板书）。3+7=10，这是一个等式还是方程？

生3：这只是一个等式。

小老师1：（边板书边问）那3+x=10，这又是什么呢？

生4：这也是一个等式，还是一个方程。

小老师1：是的，我们小组认为，等式就是含有等号的式子，而方程是含有未知数的等式。（全班掌声响起）

小老师2：我们还可以用一幅图来表示它们的关系。（边画边问）如果我们把世界上所有的等式都放在这个口袋里，那方程应该在哪呢？

生5：方程已经被装在这个大口袋里面了，应该是里面的小口袋。

小老师2：（边画边讲）是的，也就是说，方程一定是等式，等式却不一定是方程。（热烈的掌声再次响起）

2.分享有关“等式的性质和解方程”的相关知识与学习体会

师：同学们用掌声表达了赞同。那哪个小组愿意来分享第二项内容？

（另一小组的两位同学上讲台前当小老师跟大家分享，全班互动）

小老师3：（把学习单放在展台上）

大家看我们这两题解方程，解第1题的方程时用了等式的哪个性质？

生6：用了等式的第一个性质，就是在等式的两边同时加上或减去同一个数，结果仍然是等式。

小老师3：是的，我们在等式的两边同时加上6.4，得出方程的解是x=6.8。那第2题用了等式的哪个性质呢？

生7：用了等式的另一个性质，就是在等式的两边同时乘或除以同一个不是0的数，结果仍然是等式。

小老师3：是的，我们在等式的两边同时乘5，得出方程的解是x=35。

小老师4：我们小组总结了一下，发现不管是用等式的哪个性质来解方程，其实都是为了让方程的左边只剩下“x”，就得出方程的解了。（全班掌声）

师：感谢这个小组分享了用等式的性质来解方程的经验。那就让我们利用这些经验来解方程。

屏幕显示题目：x÷9=90 x-54=18，学生独立解方程。

师：来吧，谁愿意跟大家讲讲是怎么解的？

生8：我在等式的两边同时乘9，这样等式的左边就剩下x，所以x=810。（掌声）

生9：为了把方程左边的“-54”抵消，我在等式的两边同时加54，我算得x=72。（掌声）

师：老师发现英哲同学做得跟大家有些不一样，英哲，你能跟大家讲一讲吗？

生10（英哲）：我是这样想的，在等式的两边同时乘9，那么左边“÷9”跟“×9”正好可以抵消，所以我就把它们想在心里，直接写x=90×9。

师：谁能上来圈一圈，英哲把什么想在心里了？

生11上来圈：

师：那英哲这样“想在心里”的方法有什么好处吗？

生12：可以让解方程来得更简单，写起来也更方便。

师：感谢英哲的分享，让解方程的过程变得更为简洁。（全班掌声）那第2题哪些部分我们也可以“想在心里”省略不写呢？

生13上来圈：

师：以后我们解方程既可以像以前那样做，也可以用英哲“想在心里”省略写的方法。我们再练两题解方程。

屏幕显示题目：0.9x=2.43 76+x=91，生独立完成后交流，学生都自觉使用了“想在心里”的方法。

三、质疑解难

师：老师从同学们的眼睛里读出了智慧与自信。又到了“我是小问号”的时刻了。

1.小组交流

师：拿出我们的错题集，看看自己整理的错题以及“我是小问号”部分，还有哪些不理解的地方吗？先在小组里解决，小组内不能解决的，一会儿再全班交流讨论。（上图是学生错题集的部分内容）

小组交流、讨论。

2.全班讨论

师：还有哪些问题需要全班讨论的？或者虽然你们已经解决了，但觉得这个问题也值得全班分享？

生14：71+29=x，这是不是方程？

生15：10-（ ）=2是不是方程？

生16：20÷x=4，这个方程怎么解？

师：我们来整理一下，这三个问题大概可以分成两类，一类是“是不是”方程的问题（板书：是不是），一类是“怎么解”方程的问题（板书：怎么解）。我们一个一个来研究讨论。

师：我们先看第一个问题，认为它是方程的举手。（大部分同学举手）

师：认为它不是方程的举手。（4个同学举手）

师：来吧，都来说说理由吧。

生17：71+29=x不仅是等式，而且还含有未知数，所以它是方程。

生18：不对，这个x没有意义。

生19：可它是含有未知数的等式呀！

生20：我们可以把x用手盖住，发现71+29已经是一个完整的算式了，所以这个x完全没有用。

师：咦，我们可以读一读其他几个方程，来体会体会他们所说的“没有意义”和“没有用”。

生齐读：3+x=10，x÷9=90，x-54=18。

师：跟这几个方程比，（指71+29=x）这里的未知数x有什么特殊的呢？

生21：这里的x单独在右边，而其他的方程中，未知数跟已知数在一起的。

师：是啊，在这些方程里（指刚读的3个方程），未知数与已知数是平等的，未知数也参与了列式；而在71+29=x中，x待在等号后面不干活。

生20：所以我认为这个未知数x根本没有意义，71+29=x也就不能算是方程。

师：知道吗？关于这是不是方程的问题，老师们也一直争论不休，张老师在自己的QQ空间里转载了很多专家的说法，也写了自己的一些思考，同学们想阅读吗？

生齐：想！

师：建议大家在阅读前、阅读后都要有自己的思考，形成自己的观点。但有一点我们必须承认，正如刚才大家所说的，在71+29=x中，未知数x没有意义、没有用，所以以后我们自己列方程解决实际问题时，尽量不要列成这个样子。

师：再来看第2个问题，10-（ ）=2是方程吗？

生22：是方程，因为“（ ）”也可以表示未知数，所以这是含有未知数的等式，而且这个未知数还参与列式了。（全班掌声）

师：最后一个问题，怎么解方程20÷x=4？大家试试看吧。

（学生尝试解方程后交流）

生23：我是根据等式的性质来解的。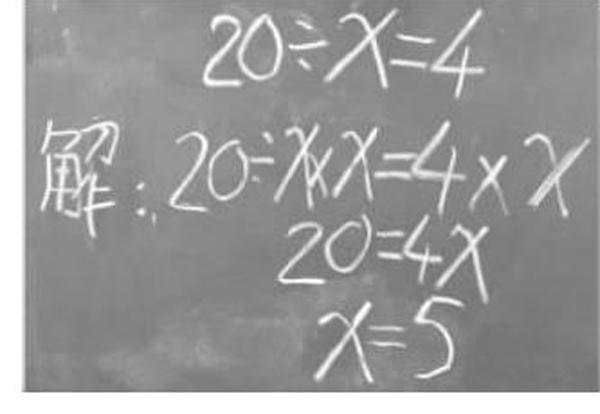

师：他的解法跟我们以前的解法有什么不一样？

生24：这种解法也是利用了等式的性质，但是以前都是在等式的两边同时加、减、乘、除以同一个数，而这里是同时乘x。（掌声）

生25：我是根据未知数的位置来解的。未知数是除数，所以就等于20÷4。

生26：我还有一种方法，我在等式的两边同时除以4，这样方程就转化成5÷x=1，这样就知道x=5。

师：这么多不同的方法，大家觉得有什么相同的地方吗？

生25：不管哪种方法，都是想办法让方程的左边只剩下x。（掌声）

师：解决了“是不是”与“怎么解”的问题，我们再来研究“为什么” （板书：为什么），为什么要学方程呢？

生27：方程可以解很多难题呢。

师：关于方程的魅力我们可以一起来体会。我们来进行一个小竞赛。当屏幕上的题目出示完毕，我们比一比，谁最先举手，能用方程表示题目的数量关系。

屏幕显示：今天早上，8路公交车从江苏路站出发时，车上有x人。到傅佐路站时，下去4人，上来6人；到西流湾公园站时，又下去5人，上来9人。这时，车上有12人。那么从江苏路站出发时，车上有多少人？

（题目出示完毕，几乎全班举手）

生28：x-4+6-5+9=12。（全班掌声）

师：这么复杂的数量关系，你们是怎样又快又对地列出方程的呢？

生29：我们只要按着题目的意思顺着写就行了。

师：多形象的一个词啊！“顺着写”，知道吗？“顺着写”是方程最大的魅力！

师：关于方程的魅力我们继续来体会。

屏幕显示：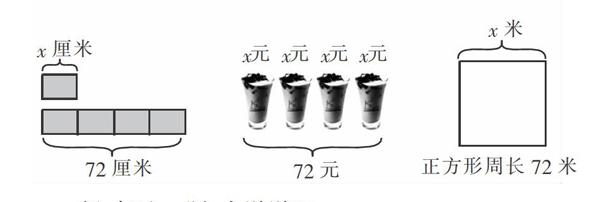

师：任选一题，来说说吧。

生30：我选第3幅图，4x=72。

生31：我选第1幅图，4x=72。

生32：我选第2幅图，4x=72。

师：咦，图不同的呀，为什么列出的方程却相同呢？你还能试着编一道用4x=72表示的题目吗？

生33：小芳每天看书x页，4天看了72页。（掌声）

生34：四个同学都有x张邮票，一共有72张邮票。

（还有很多同学继续举手）

师：这样的问题能编得完吗？

生齐：编不完。

师：是啊，一道方程竟然可以表示无数个问题，一个方程竟然有如此强大的概括性，这也是方程的魅力。

四、考考自己

师：真诚地祝贺大家在分享的同时，又有了那么多的体会与收获！最后，让我们来“考考自己”。学习单的反面，独立完成。

1.看图分析数量关系，并列方程解答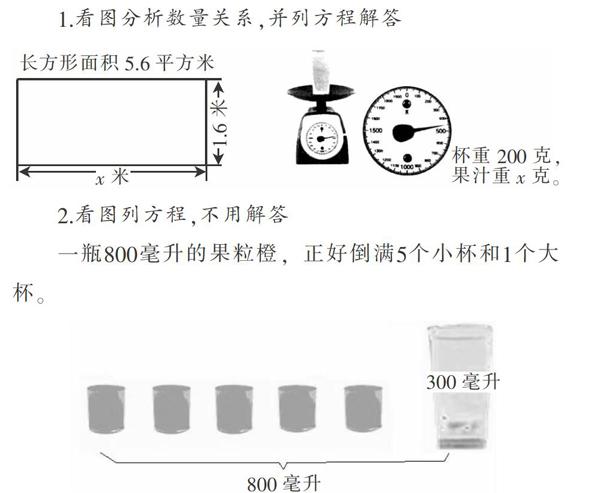

2.看图列方程，不用解答

一瓶800毫升的果粒橙，正好倒满5个小杯和1个大杯。

课后思考：

周国平说：“教育不是制造，学生不是产品。所以衡量教育质量，不可能用外在的需要、外在的目的来制造机械产品，来制定指标，用指标来衡量。所以，要提高教育质量，一个前提就是把学生当成人，了解学生的生长，对他们的培育处于什么样的状态。”如果说我们要真正做到教育目标上以人为本，教学方式上人性化，那么学生在中央的数学课堂不仅是一种境界，更是一种积极状态。

学生在中央的数学课堂，首先把学生看成一个真正的人。把学生当成人性意义上的人，让他在数学学习中体会到人性的丰富、做人的尊严、做人的快乐，享受数学学习的乐趣，从而得到更大的发展；其次关注个性的发展，把每个学生看成独特的个体，让他最好的禀赋能够显示出来，得到发现，得到发育。

《“方程”分享会》是在学生学完“等式和方程”“等式的性质与解方程”后的一节练习课，但它又与一般的练习课稍有不同，是让学生以分享的形式进行自主交流与自觉练习，并在自由分享的过程中提升认知的一节“学生在中央”的数学课堂。值得一提的是，这样的课型不是公开场合的作秀，“分享会”“经验发布会”“讲评会”等一系列课型，是我们琅琊路小学开发的数学常态课堂。“分享会”所呈现的一些课堂环节也是平时课堂的一些常态动作，如“数学分享”时刻、“我是小问号”时刻，等等。

在今年3月3日举行的南京市小学数学教学现场会上，本课向全市的领导、教师开放，南京市教研室朱宇辉主任评价：这是一堂表达学生学习力的数学课，更是一堂提升学生学习力的数学课。《“方程”分享会》绝不是一堂精雕细琢的课，甚至不是一堂可以“试上”与复制的课，说得更直白些，它就是一堂学生在中央的数学裸课，为什么能得到专家的赞叹呢？我想这也正应了“最常态的课便是最好的公开课”这句话。

认真思考本课，以下几点表达了学生在中央的教学理念：

1.学习经验源自于学生的真切感受——真分享

课开始时的“热情分享”，学生始终以“主人”的角色参与活动。小组分享时，学生们围绕主题轮流说自己的认识与学习体会。每个同学既要说清楚自己的体会，还要听懂别人的认识，最后还要综合本小组的经验，以便全班分享。我们看到：有的小组在组内分享时有相互纠错的过程，有的小组有相互质疑的行为，更多的是相互补充与提醒。小组分享弥补了教师无法面面俱到的缺憾，让课堂里所有的声音都得到了关注与承认，同时也锻炼了学生彼此聆听的能力。

在“全班分享”时，同学们又呈现了属于他们的精彩。“我们小组认为，等式就是含有等号的式子，而方程是含有未知数的等式。”“如果我们把世界上所有的等式都放在这个口袋里，那方程应该在哪呢？”“不管是用等式的哪个性质来解方程，其实都是为了让方程的左边只剩下‘x，就得出方程的解了。”……学生们的语言是稚嫩的，也许还不够完美、不够科学，但它们却是学生们自己的真切感受，是学生们自己的独特体验。

学生在前几节课的学习中，只是初步学会了解方程，如何帮助他们掌握解方程的方法，形成相应的技能呢？在一般的课堂里，一定有老师的说教，可在这里只有学生彼此之间的分享。英哲同学的解法跟大家不一样，英哲分享说：我是这样想的，在等式的两边同时乘9，那么左边“÷9”跟“×9”正好可以抵消，所以我就把它们想在心里，直接写x=90×9。老师抓住“想在心里”这一策略，使解方程的过程更加算法化。同学们通过比较、评价不同的方法，在算理与算法并行的同时，掌握了解方程的技能，让解方程的过程更简洁，让解方程的思考更加流畅，也与中学里解方程的“移项”等方法相接轨，有利于提升解方程的能力。

正因为分享的学习经验都是学生的亲身体会，所以在整个“热情分享”时刻，课堂氛围始终如此轻松、自然、平等，学生不必严肃拘谨，没有正襟危坐，有的只是愉快的分享、此起彼伏的掌声和彼此会心的笑脸。学生真正地站在了课堂的中央，真实地拥有了一个乐于表达的课堂、促进自我内在对话的课堂。

2.研究问题源自于学生的真实疑惑——真研究

在质疑问难环节，同学们首先以自己的错题集为载体，根据整理的错题及记录的“我是个小问号”内容，开展自我剖析与互相帮助的小组活动。有的同学在小组里坦诚地说出自己的错题经验，有的同学在小组里寻求帮助，也有的同学相互一起交流、争论着某一问题。此时，每个学习小组都是一个学习共同体，每个同学都能在小组里实现自己的价值，并获得看得见的生长。

学生以主人的姿态交流自己的学习，包括自己的问题与疑惑，有些疑惑在小组内得到了解决，也有些疑惑小组内不能解决，于是就有了全班讨论。在全班讨论阶段，同学提出了“71+29=x”与“10-（ ）=2”是不是方程的问题，还提出了怎么解方程20÷x=4的问题。对于学生提出的问题，教师没有只是作出简单的解答，或者是苍白的说理，而是依然让学生站在课中央，把话语权给学生。学生对于71+29=x是不是方程的问题，尽管有两种不同的意见，但在学生的争论中，我们惊喜地看到学生对于方程内涵的理解：方程不仅仅是含有未知数的等式，更是把未知数摆到与已知数同等的位置参与列式。

学生在中央的数学课堂的关键是体现“人”与“人性”，“71+29=x”是不是方程的问题是教育界一直争论的问题，教师没有回避，而是选择了直面，更是在学生争论后，善意地告诉学生，教师在自己的QQ空间里写了关于这个问题的思考，并转载了许多专家的观点，引导学生去再阅读、再思考，形成自己的观点。学生与教师是如此地平等，包括机会的平等、表达的平等、精神的平等……学生的学习不会因为40分钟的结束而停止，学生在中央的数学课堂是促进学生41分钟发展的课堂。

无论是对于“是不是”方程的问题，还是“怎么解”方程的问题，因为都是学生自己的真实疑惑，也就有了学生全身心的投入与热情，学生始终以小主人的姿态主动、自觉地研究问题。

3.学习习惯源自于学生的真情经历——真养成

数学学习一直强调良好的学习习惯，可良好的学习习惯哪里来？一定不是仅凭单调的说教就能形成的。本课学习中，学生表现出了优秀的学习习惯，包括课堂学习习惯与课后作业、思考习惯等。具体如错题整理的习惯，及时记录问题、研究问题的习惯，合作学习、相互质疑、懂得分享的习惯，等等。

课上完后，听课老师们纷纷上来，查看学生的错题集，发现我们学生的错题集上有与众不同的一栏，那就是“我是个小问号”部分，同学们会在这一栏里随时记录自己的问题，以便共同研究与探讨。听课老师们还索要了学生们的课堂学习单，发现学生在课堂学习时，善于用自己的方式记录自己的思考，愿意把自己的思维过程展示给自己的同伴。

听课老师们疑惑：为什么这些学生拥有如此好的学习习惯呢？没有更多的理由，这些都只是同学们的日常行为，也许一开始还有些制度化的成分，可当学生们亲身经历，品尝到学习的快乐与成功的喜悦后，这些“习惯”也就成为学生们自己最自然的需要与最真实的学习品质了。

最后，值得一提的是：学生在中央的课堂并不是教师不作为的课堂，而是对教师提出了更高的要求，要求教师有更智慧的作为。如在本课的质疑问难阶段，学生们提出了“是不是”与“怎么解”的问题，老师在此基础上又提出了“为什么”的问题。通过一系列的真实经历，学生真切体会到了方程“顺着写”的魅力，也感受到了方程是一种模型的思想，认识上了一个层次。

张奠宙教授认为，数学的核心素养有“真、善、美”三个维度，而本课的“真分享”“真研究”“真养成”，旨在引领学生以学习小主人的角色自觉探索数学真理、热情感受数学思想方法、主动欣赏数学智慧之美，帮助学生提高数学学习力，逐步拥有数学品质，并最终形成数学素养。

综上所述，学生在中央的数学课堂是儿童的数学课堂：课堂不再“秀”教师，而是儿童自由表达的舞台；课堂不再是戏场，只追求精致美、流畅美、细腻美，而是更关注学生体验解放感、震撼感、力量感；课堂不再只是教学内容的落实，而是对数学的快乐享受，更是儿童生命的美妙拔节！学生在中央的数学课堂指向儿童的数学核心素养，促进儿童的生命成长，它着力表达了数学课堂教学的理念：打造第一人称视角的课堂，快乐的课堂，促进41分钟发展的课堂。？筻