双目立体视觉在人形机器人三维重建中的应用

孙新领 谭志伟 杨观赐

摘 要： 提出一种基于双目视觉的机器人三维（3D）重建方案，将两个LifeCam VX6000摄像机安装在NAO人形机器人脸部，分别采集目标的左右图像。在3D重建过程中，利用棋盘格的角点定位对摄像机进行标定，对图像进行校正去除畸变，利用Canny检测算子来提取图像的边缘特征，进行立体匹配，利用Delaunay三角剖分算法对二维图像进行三角剖分，并将图像纹理映射到三维空间，同时对立体目标图像进行渲染，获得最终的3D重建图像。实验结果表明，该方案能够精确的进行深度测量，实现场景的3D重建，能够很好的用于人形机器人应用场景。

关键词： 双目立体视觉； NAO机器人； 三维重建； Delaunay三角剖分

中图分类号： TN911.73?34； TP391 文献标识码： A 文章编号： 1004?373X（2016）08?0080?05

Application of binocular stereo vision in 3D reconstruction of humanoid robot

SUN Xinling1， TAN Zhiwei 1， YANG Guanci2

（1. Department of Computer Science， Henan Institute of Technology， Xinxiang 453003， China；

2. MOE Key Laboratory of Advanced Manufacturing Technology， Guizhou University， Guiyang 550025， China）

Abstract： A three?dimensional （3D） reconstruction scheme based on binocular vision is proposed. Two VX6000 LifeCam cameras are installed in the NAO humanoid robot's face to collect the left and right images of the target. In the process of 3D reconstruction， the camera is calibrated by utilizing the tessellated corner point positioning， the image is corrected to remove its distortion， and then the edge features of the image are extracted by Canny edge detector for stereo matching. Finally， the 2D image is triangulated by Delaunay triangulation， the image texture is mapped to the three?dimensional space， and then 3D target image is rendered to obtain the final 3D image. The experimental results show that the proposed scheme can accurately measure the depth of the scene， and can be used in the 3D reconstruction of the humanoid robot scene.

Keywords： binocular stereo vision； NAO robot； three?dimensional reconstruction； Delaunay triangulation

0 引 言

三维（Three?Dimensional，3D）重建在机器视觉领域具有很好的应用前景，能够使机器人完成许多高危险性任务，如矿井救援等[1]。相比于传统的声纳和红外感知系统的感知质量较差且易受环境影响，与人类类似的视觉系统具有较强距离评估和模式识别能力，因此，立体视觉3D重建技术成为未来研究热点[2]。然而，目前大多研究者只提出一些理论，很少对立体视觉3D重建技术的实际应用进行研究。

文献[3]提出了一种面向移动机器人的低成本3D感知系统，利用一个普通2D激光测距仪，一个步进电机和一个摄像机完成3D重建过程，然而，在测试过程中作者假设了很多限制条件。2010年，微软推出一种智能识别设备：Kinect，其集成了RGB摄像机、麦克风和深度传感器，具有3D运动捕捉、人脸识别等功能。文献[4]利用微软的Kinect设备提供的深度数据，提出了一种室内3D重建方法，然而其重建精度不高。文献[5]中提出了一种面向移动机器人的3D感知系统，利用双目立体视觉系统构建3D模型，但其在立体匹配过程中采用的是简单的特征点匹配，匹配精度较低。本文将基于双目立体视觉进行3D重建置于机器人上，选取应用广泛的Aldebaran Robotics公司的NAO人形机器人作为载体。在机器人脸部安装两个微软LifeCam VX6000摄像机用来采集目标的左右图像。在3D重建过程中，利用棋盘格的角点定位对摄像机进行标定；利用Canny算子来提取特征进行立体匹配；利用Delaunay三角剖分算法对图像进行三角剖分，并映射到三维空间，同时对立体目标图像进行渲染，获得3D重建图像。实验结果表明，本文方案能精确的进行场景的3D重建，深度测量误差能够达到1%，在移动人形机器人领域具有很好的应用前景。

1 机器人双目视觉模型

1.1 NAO机器人双目摄像机装置

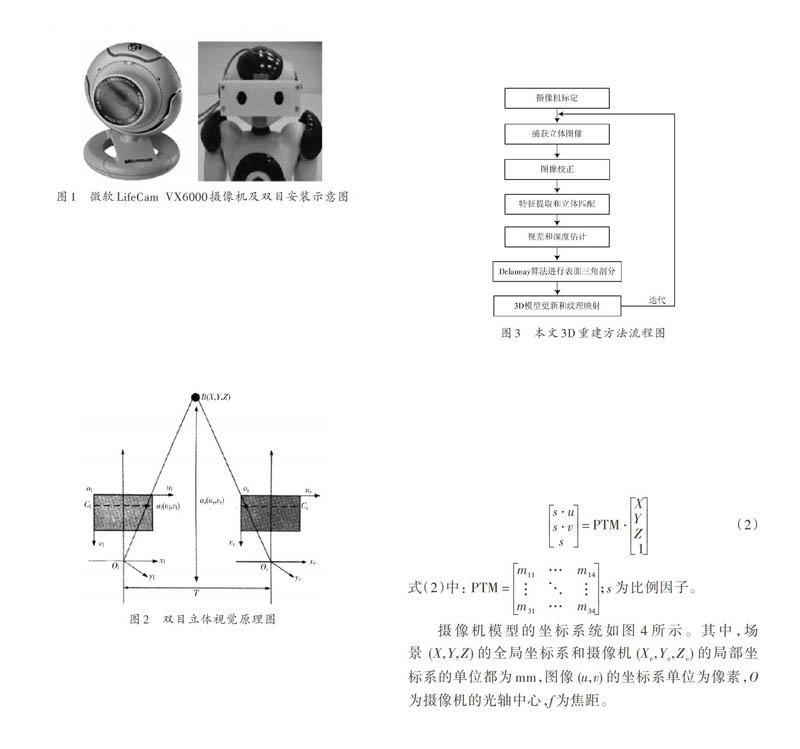
双目摄像机是模拟人眼，将两个摄像机的孔径平面设定为特定的距离（约为6.5 cm）。由于NAO机器人内置的两个摄像机的视觉场景没有发生重叠，因此不能用于构建双目立体视觉[6]。所以，本文在机器人头部前方安装两个微软LifeCam VX6000摄像机，如图1所示。

1.2 双目立体视觉原理

双目立体视觉主要是利用目标点在左右两幅视图上成像的横向坐标差异来构建立体图像。本文使用2台相同属性的VX6000摄像机，成像平面垂直于系统光轴，理论上2台摄像机在X轴方向重合，在T轴方向平行，2台摄像机光心沿X轴方向的距离为T。双目立体视觉原理如图2所示。

目标点B在左右2幅图像上成像时，横向坐标存在直接差异（即视差），与目标到成像平面的距离Z存在反比例关系[7]：

[Z=fTd] （1）

为了得到目标点的3D空间距离Z，则需要获知摄像机焦距[f]，视差d，光轴距离T；若要获得x和y的坐标，还需获知摄像机成像平面坐标系与立体坐标系原点的偏移量[Cu]和[Cv]，其中一些参数可通过摄像机的标定获得[8]。

2 本文双目立体视觉3D重建方法

本文提出一种用于人形机器人的基于双目立体视觉的3D重建方法，其流程图如图3所示。第一步，为摄像机标定，提取立体摄像机的内部和外部参数；第二步，执行图像处理程序，首先从摄像机获取立体图像对，然后执行图像校正过程；第三步，利用Canny检测算子提取图像的边缘特征，进行立体匹配；第四步，进行深度估计，获得三维坐标，利用Delaunary算法将三维坐标关联到二维平面，并对表面进行三角形剖分；最后，更新3D模型，将图像纹理映射到三维空间。

2.1 摄像机标定

摄像机标定过程实际上是获得摄像机的内部参数和外部参数过程。本文利用投影变换矩阵（PTM）[9]对摄像机进行标定。PTM为一个正交矩阵，将3D坐标系中的场景点[[X，Y，Z]T]与2D坐标系中的图像点[[x，y]T]进行关联，如下所示[10]：

[s?us?v s=PTM?XYZ 1] （2）

式（2）中：[PTM=m11…m14???m31…m34；][s]为比例因子。

摄像机模型的坐标系统如图4所示。其中，场景[（X，Y，Z）]的全局坐标系和摄像机[（Xc，Yc，Zc）]的局部坐标系的单位都为mm，图像[（u，v）]的坐标系单位为像素，O为摄像机的光轴中心，f为焦距。

图4 摄像机坐标系模型

[PTM（mij）]中的元素是摄像机内部和外部参数的线性组合。内部参数包含摄像机和透镜的属性（像素大小、焦距[f]、图像光轴中心的坐标[（u，v）]、[Cu]和[Cv]），外部参数为旋转角度和平移距离[11]。理想的针孔模型不需要任何透镜就能够投影成像，但在实际操作中，需要一个透镜才能正常工作，然而，这个透镜通常会引起3D点投影到图像平面的过程发生畸变。透镜畸变可以分为径向畸变和切向畸变[12]，这两种畸变的建模如下所示：

[xcorrycorr=（1+k1?r2+k2?r4+k3?r6）?xy+ 2?p1?x?y+p2（r2+2?x2）p1（r2+2?y2）+2?p2?x?y] （3）

式中：[（x，y）]为图像中畸变点的初始位置；[（xcorr，ycorr）]为校正后畸变点的新位置；[k1]，[k2]和[k3]为径向畸变系数；[p1]和[p2]为切向畸变系数。

通过摄像机标定可获取畸变参数和PTM中的元素。由PTM的外部参数可在立体视觉标定过程中将摄像机的位置进行关联。本文利用棋盘格模板，通过编写的自标定程序，采集棋盘格左右立体图像，提取棋盘角点来对摄像机进行标定，求出PTM中的元素。在标定开始阶段，加载每一张图像，并检测棋盘角点（8×6=48），然后在每个角点处利用亚像素定位算法[13]提高角点的定位精度。该算法是使用角点附近灰度梯度特征进行迭代求解的方法，角点定位见图5。标定过程能够去除图像中畸变，图像中每个角点的外极线可在其他图像中计算出来，但也存在一定的标定误差（平均误差为0.63个像素）。

图5 摄像机标定过程中棋盘格的角点定位

2.2 图像校正

在3D重建中，需要两个摄像机的焦距、主焦点具有相同坐标（[Cleftx=Crightx]）且图像行对齐。另外，需要摄像机拍摄的图像不失真；两个摄像机对齐，且图像平面都平行于光轴；两个图像平面恰好共面等条件。

通过摄像机标定，可固定摄像机的主焦点坐标为相同的值。但是，两个摄像机的主光轴并不平行，传感器平面并不共面，所以需要利用图像校正来解决该问题。图像校正处理过程中，考虑摄像机间的相对位置，将图像点的坐标转换为一个满足上述条件的框架中的坐标。

本文利用每个摄像机在标定过程中获取的畸变系数（即径向和切向）计算出无畸变的图像。在图像校正中，使用了摄像机参考系统（摄像机标定过程中计算出的旋转角度和平移大小）之间的空间关系。通过确保两个摄像机的图像平面相同，从而使所有的外极线平行，这样，每个图像的校正变换就可以简化立体匹配问题。

图像校正中，图像会扩展到角落，使两个图像外围产生宽度达20个像素的无用灰色区域。为了去除这些灰色区域，本文设定ROI的起点坐标为（20，20），宽度和高度分别为600和400（如图6（a）所示）。

重建过程中，两幅图片的非重叠区域也是无用的，且会增加提取特征和匹配过程中的计算量。通过计算重叠区域大小，本文裁减掉两个图像两侧宽度为75个像素的非重叠区域（如图6（b）所示）。

2.3 特征提取及立体匹配

在立体匹配之前，首先要进行特征提取，本文采用Canny算子[14]来提取图像的边缘特征。边缘特征是图像周围像素灰度有阶跃变化的像素集合，是图像的基本特征。为精确定位边缘，利用非极大值抑制，只保留幅值局部变化的最大值，Canny算法在3×3领域内对梯度幅值阵列中的所有像素沿梯度方向进行梯度幅值插值，利用双阈值法分割得到两个阈值边缘图像，并把边缘连接成轮廓。立体匹配的实质是寻找同一场景的2幅图像序列中的共轭对点，将一幅图中的像素点映射到另一幅图像中相应位置，并求出对应点的视差值，生成深度图。

针对传统基于特征的立体匹配只能获得稀疏匹配点和基于区域的立体匹配的深度不连续问题，本文利用一种基于边缘约束的立体匹配算法[15]。首先对图像边缘采用特征匹配，使边缘特征点得到准确匹配；然后在边缘特征点匹配结果的约束下，对非边缘特征点采用区域匹配；匹配流程图如图7所示。

2.4 3D重建和纹理映射

根据立体摄像机标定、特征提取和立体匹配所获取的信息，通过式（4）～式（6）即可计算获得特征点的3D坐标。然后，利用Delaunay三角剖分算法[16]将3D坐标与2D空间中的坐标相关联，Delaunay三角剖分算法在2D空间中创建一个三角形的点集合，并确保单个三角形的外接球（在本文中为圆形）中没有节点（空球面属性），以此将每个点连接到其自然领域。

深度估计计算表达式如下：

[Z=f?Txl-xr] （4）

式中：[Z]表示摄像机框架中的深度；[f]表示焦距；[T]表示校正处理后两个摄像机主轴间的距离；[xl]和[xr]表示图像帧中同一个3D点在[x]轴的投影坐标。在获取[Z]之后，可利用下式计算[x]和[y]的坐标值，从而获得物体的3D点坐标[（X，Y，Z）]。

[X=Z?x-Cxf] （5）

[Y=Z?y-Cyf] （6）

根据图像中的三角剖分，实现对3D模型的更新并结合图像纹理一起映射到3D空间，实现3D重建。利用OpenGL（开放图形库）来渲染立体目标，并根据视角位置对目标视图进行更新。

3 实验结果及分析

3.1 深度测量实验

本文利用图像处理库OpenCV（开放资源机器视觉）和OpenGL编写软件，采用一个具有蓝色滑动带的铝杆作为实验对象，进行深度测量实验。实验环境为一个大小240 cm×240 cm的矩形区域，为了减少图像处理阶段的计算量，将矩形区域的四周涂成白色，高度为35 cm的墙，如图8所示。

实验中共测量40次，每次移动铝杆10 cm直到双目所看到两点间的读数为230 cm为止，测量获得深度数据如图9所示。

图10（a）中给出了深度与视差的关系图，可以看出，深度与视差成反比例函数。图10（b）给出了深度测量误差，可以看出，在一个较小范围内（小于50 cm），本文方法的测量误差保持在1 cm以内，当深度增加时，误差值最大达到3 cm。图10（c）给出了测量视差误差，可以看出，需要利用较大的视差（大于150个像素）来确保误差在1 cm以下。对于NAO机器人导航来说，误差值在1～3 cm之间是可行的，若误差值超过3 cm，那么与障碍物发生碰撞的几率就会增大。深度测量的平均百分比误差（APE）和平均误差（AE）采用下式计算：

[APE=1NDi计算-Di测量Di测量×100%=1.06%] （7）

[AE=1NDi计算-Di测量=-0.907] （8）

3.2 3D重建实验

在场景3D重建实验中，本文以一个盒子作为目标，利用本文方法对其几何外形进行测量并将测量结果与实际尺寸进行比较，从而获得模型的重建精度，如图11所示。

实验结果表明，盒子的高度（20 cm）和长度（45 cm）的计算结果误差小于0.3 cm，且位于盒子相同垂直边缘的点P1和P2的Z坐标差值小于0.9 cm。另外，计算得出P1，P2与P1，P5连线之间的角度为90°，如图12所示。

另外，构建了不同场景（不同形状的盒子和散落分布的圆形元素），并对场景的3D模型进行提取和渲染，如图13和图14所示。结果表明，重建精度与先前测试获取的精度相似。

4 结 语

本文提出一种基于双目视觉的机器人3D重建方案，能够用于机器人避开障碍物或感知目标物体。将两个LifeCam VX6000摄像机模拟人眼间距安装在NAO机器人脸部，利用棋盘格的角点定位对摄像机进行标定。在重建过程中，利用2个摄像机采集图像，并对图像进行校正去除畸变。利用Canny检测算子来提取图像的边缘特征，进行立体匹配。利用Delaunay三角剖分算法对二维图像进行三角剖分，并映射到三维空间，同时对立体目标图像进行渲染获得最终的3D重建图像。实验表明，该方案能够精确地进行深度测量，实现场景的3D重建。然而，当机器人距离目标的距离较远时，本文模型精度就会下降。所以在今后，将进一步提升本文方案的性能，使NAO机器人能够远距离感知目标。

参考文献

[1] 李丹程，刘景明，姜琳颖，等.基于栅格模型的双目移动机器人三维场景重建[J].小型微型计算机系统，2012，33（4）：873?877.

[2] CAULI N， GASPAR J A， BERNARDINO A， et al. An expected perception architecture using visual 3D reconstruction for a humanoid robot [J]. Intelligent robots & systems， 2011， 10（1）： 4826?4831.

[3] DAN?CHENG L I， LIU J M， JIANG L Y， et al. Binocular mobile robot 3D scene reconstruction based on evidence grid model [J]. Journal of chinese computer systems， 2012， 33（4）：873?877.

[4] 夏文玲，顾照鹏，杨唐胜.实时三维重建算法的实现：基于Kinect与单目视觉SLAM的三维重建[J].计算机工程与应用， 2014，50（24）：199?203.

[5] TAMAS L， GORON L C. 3D semantic interpretation for robot perception inside office environments [J]. Engineering applications of artificial intelligence， 2014， 32（6）： 76?87.

[6] 袁丽，田国会，李国栋.NAO机器人的视觉伺服物品抓取操作[J].山东大学学报（工学版），2014，44（3）：57?63.

[7] 殷小舟，淮永建，黄冬辉.基于双目立体视觉的花卉三维重建[J].扬州大学学报（农业与生命科学版），2012，33（3）：91?94.

[8] HOU R， JEONG K S， HOU R， et al. 3D Reconstruction and self?calibration based on binocular stereo vision [J]. The Journal of Korean Institute of Information and Communication Engineering， 2012， 13（9）： 3856?3863.

[9] ZHANG B L， YANG J C， LEE H R. Image space coordinates extraction algorithm based on the perspective projection transformation matrix [J]. Applied mechanics & materials， 2014， 644： 4368?4371.

[10] 王乘，武建刚，管涛，等.基于投影重建的增强现实虚实注册方法研究[J].工程图学学报，2008，29（1）：67?71.

[11] XU P H， DING X， WANG R， et al. Feature?based 3D reconstruction of fabric by binocular stereo?vision [J]. Journal of the textile institute， 2015， 107（1）： 1?11.

[12] WANG C， SHEN Y， ZHANG W， et al. Constrained high accuracy stereo reconstruction method for surgical instruments positioning [J]. Ksii transactions on internet & information systems， 2012， 6（10）： 2679?2691.

[13] 何海清，黄声享.改进的Harris亚像素角点快速定位[J].中国图象图形学报，2012，17（7）：853?857.

[14] SONG T， TANG B， ZHAO M， et al. An accurate 3?D fire location method based on sub?pixel edge detection and non?parametric stereo matching [J]. Measurement， 2014， 50（4）： 160?171.

[15] 何袱，达飞鹏.置信度传播和区域边缘构建的立体匹配算法[J].中国图象图形学报，2011，16（11）：2060?2066.

[16] 罗小华，付文超，管培祥，等.简单多边形的动态Delaunay三角剖分算法[J].暨南大学学报（自然科学与医学版），2011， 32（1）：26?30.