Re-examining Photodetachment of H−near a Spherical Surface using Closed-Orbit Theory∗

Xiao-Peng You(晓鹏)and Meng-Li Du(杜孟利)

Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China

1 Introduction

Photodetachment of negative ions in different external fields has been studied during the past decades.[1−11]The most interesting aspect of these studies is to understand and characterise the induced oscillations in various systems by the additional external fields.different methods have also been introduced to calculate the photodetachment cross sections.As a prelude to the present system,the photodetachment cross section for a negative ion H−near a reflective wall was first introduced and studied[12]using closed orbit theory.At almost the same time,Afaq and Du[13]applied a theoretical imaging method to study the same problem.More recently,Haneef et al.[14]studied the photodetachment of H−near a spherical surface by using the theoretical imaging method.[13]They found oscillations in the total photodetachment cross sections.

In this paper,we re-examine the total cross section of H−near a spherical surface by directly applying the closed-orbit theory.When we compare our result and that by Haneef et al.,significant difference between the two results is found.We also find the difference vanishes in the limit of large radius of the reflective sphere.We argue the discrepancy between the two results is caused by the incorrect application of the theoretical imaging method developed originally for photodetachment near a flat surface.

This article is organized as follows.In Sec.2,the system is briefly described.In Sec.3,the total photodetachment cross section is calculated using the standard closed-orbit theory.[15]In Sec.4,we calculate and compare our photodetachment cross sections with those by Haneef et al.[14]for various values of parameters such as the radius of the sphere and the distance between the sphere and the negative ion.Conclusions are given in Sec.5.Atomic units are used throughout this paper unless otherwise noted.

2 The System

For convenience,here we first briefly describe the system considered by Haneef et al.[14]As shown schematically in Fig.1 we study the photodetachment of H−near a spherical surface.The system is three-dimensional and Fig.1 represents only the intersection of the system with the x–z plane,assuming z-axis points upward.The reflective spherical surface is represented by the higher circle centered at O1with a radius rc.Outside the sphere is a negative ion H−located at O.The distance between the negative ion and the center of the spherical surface O1is assumed to be(d+rc).

For the photodetachment process,the initial bound state of H−can be regarded as a one-electron system.[7−8]In such state,the electron moves in a short-range potential of the hydrogen atom. In the one active electron approximation for the system,the initial bound state Ψi=B e−kbr/r,where B is the normalization constant and equals 0.31552.kbis the momentum related to the binding energy Ebof H−.Ebis approximately 0.754 eV.

When a laser is turned on,the ion may absorb a photon and the electron then moves under the fields of combined short-range potential of the hydrogen atom and the reflective sphere.The photodetachment cross section is a measure of the amount of excited electron cloud after the absorption of a photon by the negative ion.The cross section depends sensitively on the parameters of the system including the radius of the reflective sphere and photon energy.The cross section also reveals much about the motion of the excited electron after a photon has been absorbed.

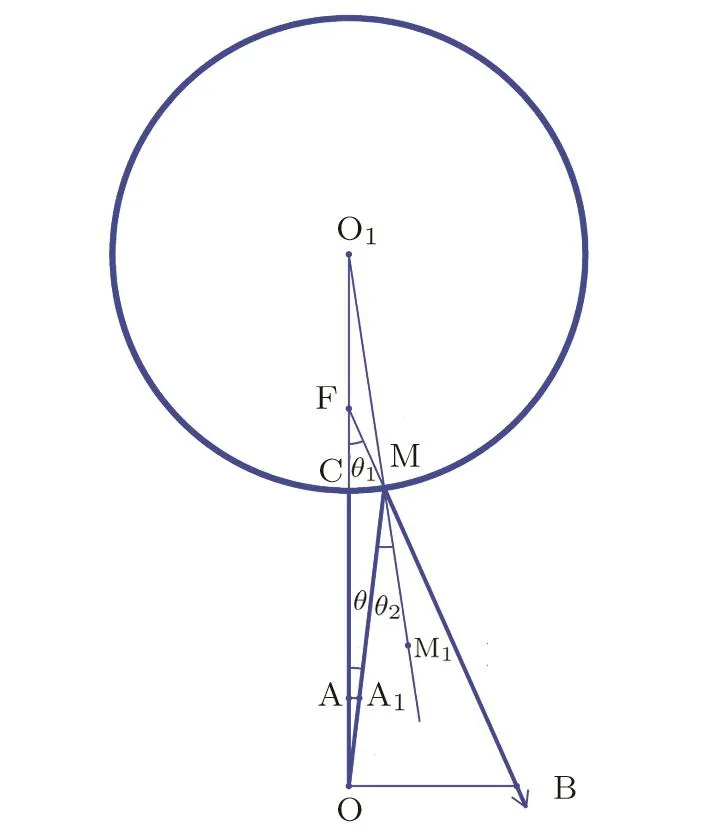
Fig.1 The schematic of photodetachment of H−near a reflective spherical surface.The radius of the reflective spherical surface centered at O1is rc.H−is outside the sphere.The distance between H−and the closest tangent plane to it is d.The origin of coordinate is set at the negative ion located at O.The z axis points upward.A trajectory from O to M and from M to B is also shown.

3 Closed-Orbit Theory for Photodetachment Cross Section

Let us assume the laser polarization is linear and parallel to the z axis.According to closed-orbit theory,[15]the active electron goes into outgoing pzwaves after a photon is absorbed.The outgoing waves emerging from O propagate away from the hydrogen atom in all directions.Suf-ifciently far from the residual atom,the wave propagates according to semiclassical mechanics.Part of these waves propagating upward toward the sphere gets reflected by the sphere.The waves then reverse its direction near the surface of the sphere and propagate downward toward the negative ion.The interference of the outgoing electron wave and the returning wave in the region of the negative ion leads to the oscillation in the photodetachment cross section.The outgoing and returning wave follows a closed-orbit.In Fig.1,the closed-orbit goes along the z-axis from O first to C and then goes back to O.This is the only closed-orbit that goes out from and returns to the point O in this system.

According to closed-orbit theory,[15]the photodetachment cross section can be written as

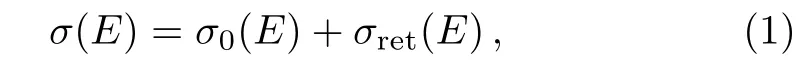
whererepresents the photodetachment cross section of H−in free space,again B=0.31522 is related to the normalization of the initial bound state Ψiof H−,c is the speed of light and its value is approximately 137 a.u.,E denotes the energy of the escaping electron,the photon energy is Ep=E+Eb.As mentioned earlier,Ebis the binding energy of the negative ion of H−. σret(E)is the oscillatory term which is identified with the closed orbit,

Epis the incident photon energy and D is the dipole operator,Ψidenotes the initial bound state wave function of H−. In the closed orbit theory,it is crucial to get Ψret,which is a returning wave obtained by propagating an outgoing wave along the closed-orbit O−C−O when it comes back to the negative ion region.In the case of linear polarization parallel to the z axis,D is simply z.

The outgoing wave is defined as the outgoing solution of an inhomogeneous Schr¨odinger equation,(E −H0)Ψout(r,θ,φ)=DΨi,where H0represents the Hamiltonian of the detached electron moving in a short-range potential excluding the spherical sphere after absorbing a photon.H0=p2/2+Vp(r),where Vp(r)represents a short-range potential for the detached electron.The outgoing wave has been obtained[8]and has the form

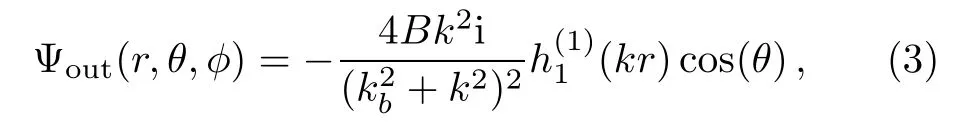
wher(kr)is an outgoing Bessel function.The outgoing wave in Eq.(3)describes the outgoing photodetached electron with an angular factor cos(θ).Far away from the source region,for example,when r is larger than 20 a.u.from the negative ion,the outgoing wave is well correlated with classical trajectories.As mentioned before,there is only one closed-orbit for this system.After a photon is absorbed,the detached electron as a wave first travels towards the sphere centered at O1.Then,it is reflected back to the region of the hydrogen atom at O by the spherical surface.Consider a small sphere centered at the negative ion.Its radius is R.For the moment,R has a value around 20 a.u.However,the final result will be independent of R as we will see.For r≥R the asymptotic approximationcan be used.Then the direct outgoing wave for the detached electron on the surface of sphere with a radius of R centered at O has the form

The returning wave function is constructed using the standard semiclassical method.[15]

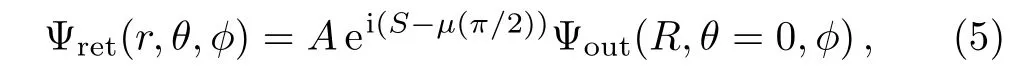
where A and S are respectively the amplitude and the action along the closed orbit,µrepresents the Maslov index and indicates the phase loss caused by the reflective spherical surface centered at O1.Assume the reflective surface is“hard”,[13]then µ equals two.In the region of the negative ion,the returning wave function can be well represented by a plane wave propagating downward,[9]Ψret=N e−ikz.Therefore,N=Aei(S−π)Ψout(R,θ=0,φ).

When the outgoing wave propagates out from the source region along the closed orbit,its amplitude and phase change accordingly.The electron travels in free space until it meets the spherical surface centered at O1,it then travels toward and finally returns back to the region of hydrogen atom.The action S along the full closed orbit O−C−O is easy to obtain,

The amplitude A is calculated with[15]

where T is the time of the full closed orbit and J(2)(ρ,z,t)is the two dimension Jacobian.

Note the elements of the Jacobian matrix are calculated with respect to the closed orbit.As shown schematically in Fig.1,when the trajectory first travels from O vertically to the sphere surface centered at O1,it is reflected at C and travels back to O,forming the closedorbit.In order to calculate the amplitude in Eqs.(7)and(8),we now launch a trajectory from O slightly away from the vertical upward direction.It first travels along OM,and then along MB.The angle between OC and OM is assumed small.

The distance between the initial point O and the reflection point M is denoted as l.For the triangle OMO1,using the law of cosines and noting O1M=rc,we have=l2+(d+rc)2− 2l(d+rc)cosθ.Solving the above equation for l,we get

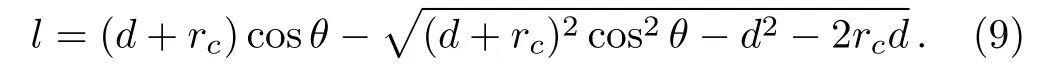
Assume the line BM is extended and it intersects the vertical line OO1at F.Similarly the line O1M is extended to M1and outside the reflective surface.To simplify the notations,we denote∠OFM= θ1and ∠OMM1= θ2.In the triangle OMO1,one may use the law of sines sin(π − θ2)/OO1=sinθ/O1M to obtain

Then because sin2θ2+cos2θ2=1,it leads to

In the triangle OFM of Fig.1,one has the relationship θ1= π − θ− (π − 2θ2)=2θ2− θ.We can use the above equation to rewrite the sine and cosine function of θ1:cosθ1=cos(2θ2− θ)=cos2θ2cosθ+sin2θ2sinθ

similarly,

Substitute Eqs.(10)and(11)to the above two expressions,one can obtain

Now we are ready to evaluate the amplitude A in Eqs.(7)and(8).When t is small and the electron is not far away from the artificial surface of sphere center at O,the trajectories are

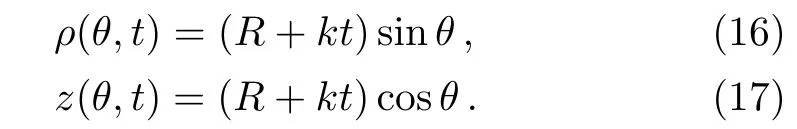
For t=0,

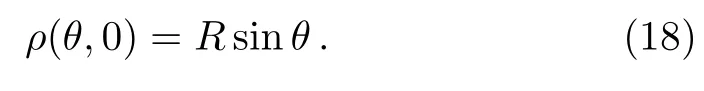
The elements of Jacobian at the initial point are obtained,

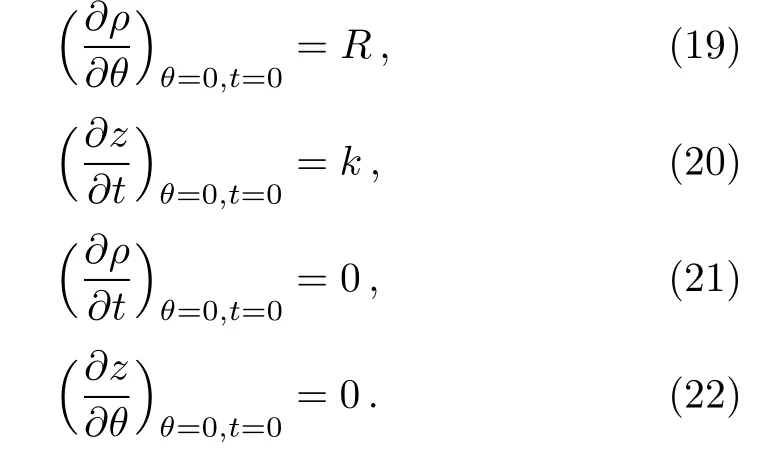
Substituting the above four elements to Eq.(8),we get

For t larger than(l−R)/k,the trajectories have been reflected by the sphere centered at O1.The returning trajectories near the region of the negative ion are given by

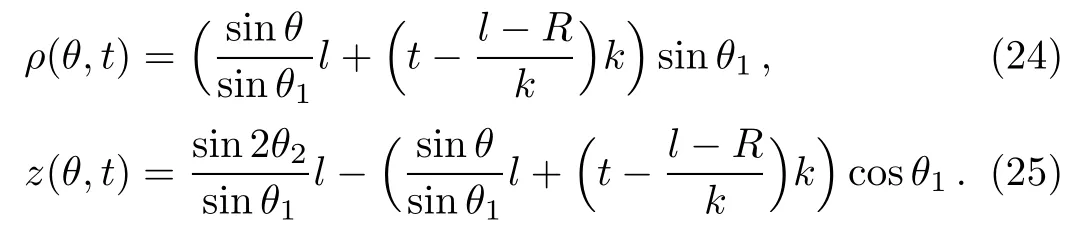
From Eq.(24)one has immediately(∂ρ/∂t)θ=0=0.So only two elements are needed to determine the Jacobian in Eq.(8)for the returning trajectory.From Eqs.(24)and(25)we have

For the closed orbit,we have also l=d and t=(2d−R)/k.

Denoting the transit time of the closed-orbit by T,we have

The Jacobian for the closed orbit at the returning time T is then

For small θ,Eq.(24)also gives the following approximation

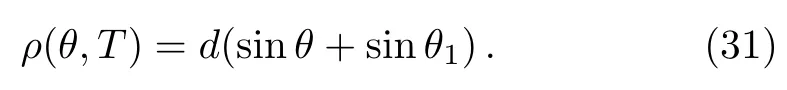
Now combine it with the expression of ρ(θ,0)obtained earlier,one can show

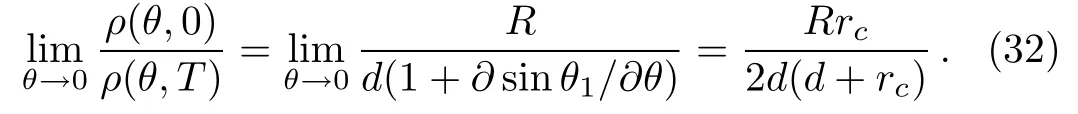
When Eqs.(23),(30),and(32)are used in Eq.(7),we finally obtain the amplitude

for the closed orbit in the present system.

Since the amplitude A primarily determines the amplitude of the oscillation in the photodetachment cross section corresponding to the closed-orbit,its importance can not be over-estimated.As a check,we now demonstrate explicitly that the expression for A in Eq.(33)satisfies the conservation of the electron fl ux.

Denoting the short arc segment AA1by ρiand the short horizontal line OB by ρf.That part of the detached electron crossing AA1must also cross OB.When θ is small and when the cylindrical symmetry of the system is taken into consideration,the electron flux crossing AA1is approximately viπρi2and the electron flux crossing OB is approximately vfπρf2,where we have used Aiand Afto represent the amplitudes of the detached electron wave when crossing AA1and OB.Since the initial speed of the electron viequals to the final returning speed vf.The conservation of electron fl ux requires

From Fig.1 we have

Therefore

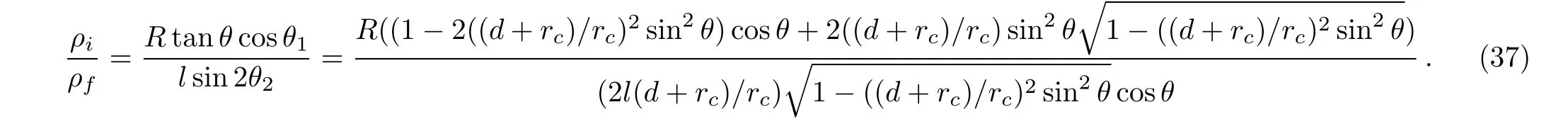
When θ approaches 0,

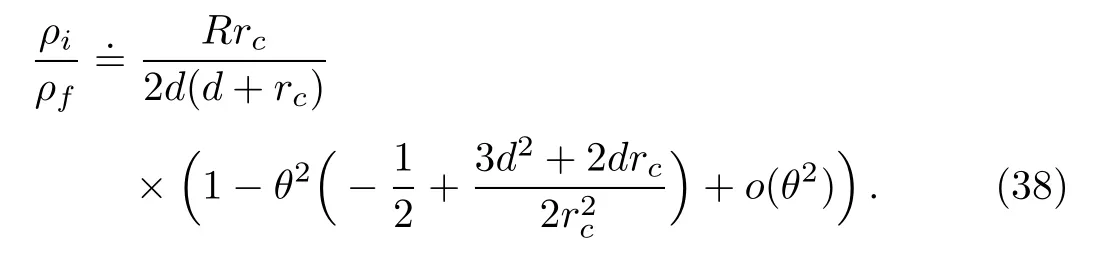
Combining Eqs.(34)and(38),we get

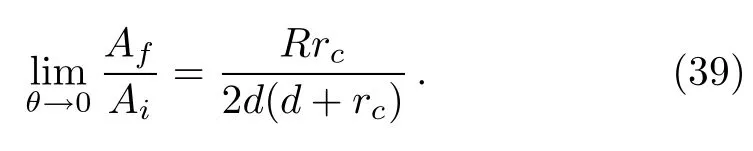
A is equal to Afby assuming Ai=1.This provides confirmation on the correctness of the result in Eq.(33).

The returning wave function near the source region is now written as

Substitute this wave function in Eq.(2),the overlap integral hDΨi|Ψreti is written as

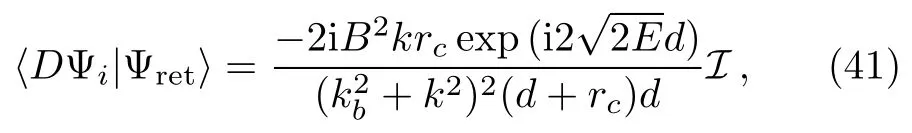
with

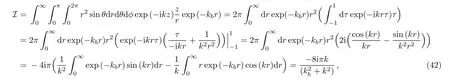
where we have used

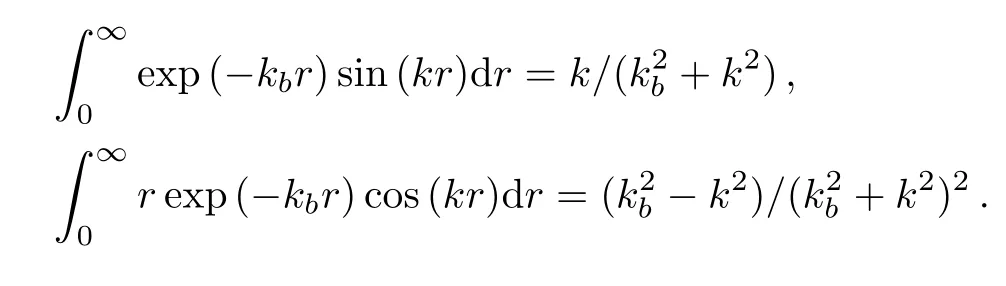
Consequently we have

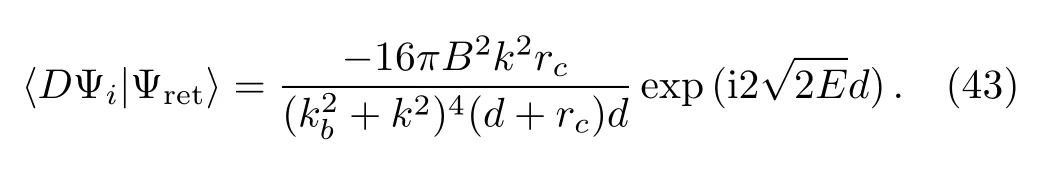
After combining the above equation and Eq.(2),we ob-tain the oscillatory part of the cross section

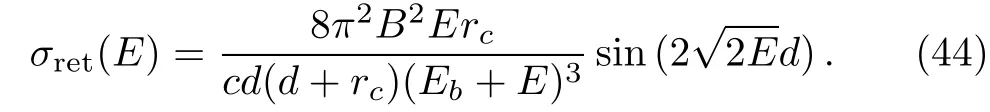
The smooth background is the total photodetachment cross section without any external fields.It has the expressionOur total photodetachment cross section using closed-orbit theory is obtained as

4 Comparisons and Discussions

We now show the results based on closed-orbit theory in Eq.(45)and compare it with the formula obtained by Haneef et al.[14]using an imaging method.For the convenience of comparison,their formula is re-written below,

where h=1+1/(1+2d/rc).In Fig.2 the results of total cross sections from both Eqs.(45)and(46)as a function of photon energy Epis plotted for d=25 a.u.and rc=50 a.u.The dashed lines represent the smooth cross section σ0(E)in free space.The thick solid line is the cross section of the closed-orbit theory calculated from Eq.(45),and the thin solid line is the cross section calculated using Eq.(46).As mentioned earlier,the oscillation in the cross section is explained as an interference between the direct outgoing wave and reflected wave in closed orbit theory.With the increase of the photon energy,the oscillation amplitude decreases.We note the difference between our result and the result of Haneef et al.[14]is very significant,especially in the phase of the oscillation.

Fig.2 The thick solid line represents the total photodetachment cross section of H−near a reflective spherical surface obtained using closed-orbit theory in Eq.(45)with d=25 a.u.and rc=50 a.u.and the thin solid line represents that obtained by Haneef et al.[14]in Eq.(46).The dashed lines represent the cross section in free space.The difference in the oscillations is significant and is discussed in the text.

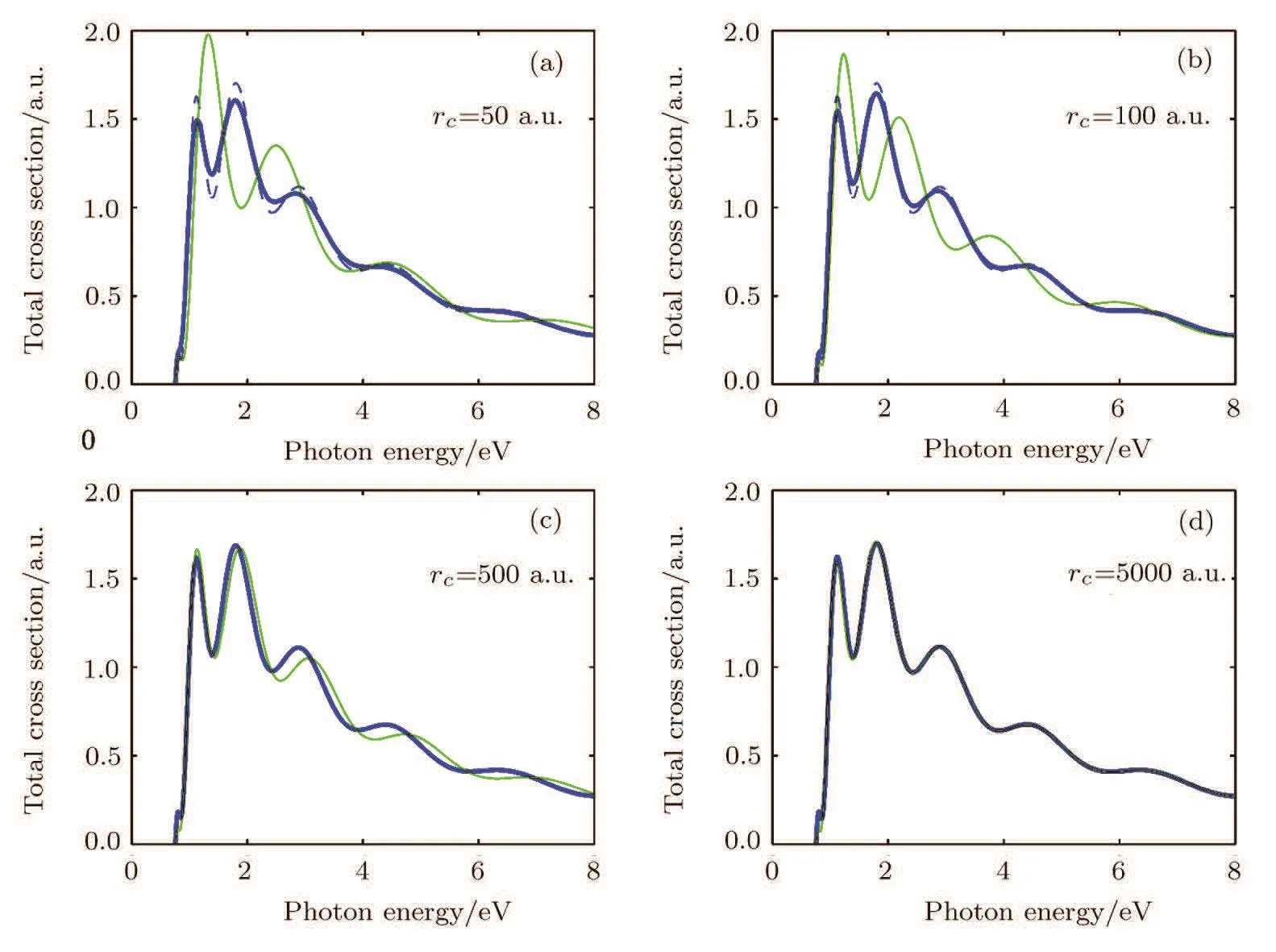
Fig.3 Similar to Fig.1 but here we fix d=25 a.u.and compare the cross sections for several values of rc.It is noted that for larger rc,the present cross sections in Eq.(45)and that obtained by Haneef et al.[14]in Eq.(46)are much closer.

If the radius of the reflective spherical surface changes,the oscillation changes accordingly.In Fig.3 we fix the distance d(indicated by OC in Fig.1)between the negative ion and the surface of the sphere and compare the total photodetachment cross sections for the radius of the sphere going from rc=50 a.u.to rc=5000 a.u.We note that in general the results from the two theories differ.But for large rc,the difference between the results of the two theories becomes smaller,and when rc=5000 a.u.the two results are almost identical as shown in Fig.3(d).In fact,one can readily show that in the limit of large radius rcthe expression in Eq.(45)is dominated by the first two terms and it approaches

The formula in Eq.(46)also approaches this limit.

The oscillation in the cross section also depends on the distance d between the negative ion and the spherical surface(OC in Fig.1).In Fig.4 the photodetachment cross sections are displayed for several values of d with a fixed rc=50 a.u.One can see the amplitude of the oscillation decreases and the cross section approaches the cross section in free space σ0(E)when d increases.On the other hand,the difference between the results from the two theories become smaller for smaller d.

Fig.4 Similar to Fig.1 but here we fix rc=50 a.u.and compare the cross sections for several values of d(the distance between the negative ion and the surface or OC in Fig.1).It is noted that for smaller d,the oscillation in Eq.(45)obtained based on closed orbit theory in the present work and that in Eq.(46)by Haneef et al.[14]agree better.

5 Conclusions

We have studied the photodetachment of H−near a reflective spherical surface using the standard closed-orbit theory.[15]Closed-orbit theory has been obtained for various systems over the decades with success.[16−19]The present system of H−photodetachment near a reflective spherical surface was first proposed by Haneef et al.[14]They applied an imaging method to study the cross section of the present system.The imaging method was originally developed for the photodetachment near a flat reflective surface.[13]Because the problem is interesting,we have studied the photodetachment cross section of it based on the closed orbit theory.We have shown the cross section in Eq.(45)based on standard closed-orbit theory differs from the cross section in Eq.(46)based on an imaging method.However,we have also observed that the difference decreases when either the radius of the reflective surface rcincreases or when the distance between the negative ion and the reflective surface d(OC in Fig.1)decreases.Larger rcor smaller d correspond to a more flat reflective surface relative to the negative ion.Inspection of the formula in Eq.(46)suggests both the phase and the amplitude are incorrect in the first dominating oscillation term.It is our belief that the imaging method originally developed for photodetachment near a flat reflective surface can not be directly applied to the photodetachment near a reflective surface of sphere as is done.[14]Further theoretical study or experiment of this system should clarify the situation and seems necessary.

References

[1]Yu.N.Demkov,V.D.Kondratovich,and V.N.Ostrovskii,JETP Lett.34(1981)403.

[2]I.I.Fabrikant,Sov.Phys.JETP 52(1980)1045.

[3]H.C.Bryant,A.Mohagheghi,J.E.Stewart,et al.,Phys.Rev.Lett.58(1987)2412.

[4]J.E.Stewart,H.C.Bryant,P.G.Harris,et al.,Phys.Rev.A 38(1988)5628.

[5]A.R.P.Rau and Hin-Yiu Wong,Phys.Rev.A 37(1988)632.

[6]A.R.P.Rau and Chitra Rangan,Phys.Rev.A 64(2001)037402.

[7]M.L.Du and J.B.Delos,Phys.Rev.A 38(1988)5609.

[8]M.L.Du,Phys.Rev.A 40(1989)4983.

[9]M.L.Du,Phys.Rev.A 70(2004)055402.

[10]N.D.Gibson,B.J.Davies,and D.J.Larson,Phys.Rev.A 47(1993)1946.

[11]N.D.Gibson,B.J.Davies,and D.J.Larson,Phys.Rev.A 48(1993)310.

[12]G.Yang,Y.Zheng,and X.Chi,Phys.Rev.A 73(2006)043413.

[13]A.Afaq and M.L.Du,J.Phys.B:At.Mol.Opt.Phys.40(2007)1309.

[14]M.Haneef,Iftikhar Ahmad,A.Afaq,and A.Rahman,J.Phys.B:At.Mol.Opt.Phys.44(2011)195004.

[15]M.L.Du and J.B.Delos,Phys.Rev.Lett.58(1987)1731;Phys.Rev.A 38(1988)1896;38(1988)1913.

[16]H.J.Zhao and M.L.Du,Phys.Rev.A 79(2009)023408.

[17]De-hua Wang,Yi-hao Wang,and Jian-Wei Li,Braz.J.Phys.43(2013)121.

[18]B.C.Yang,J.B.Delos,and M.L.Du,Phys.Rev.A 88(2013)023409.

[19]B.C.Yang,J.B.Delos,and M.L.Du,Phys.Rev.A 89(2014)013417 and references therein.