Statistical Law of High-Energy Fullerene and Its Derivatives Passing Through Graphene∗
Zhi-Cheng Xu(徐志成),Jia-Le Wen(温家乐),Wei-Rong Zhong(钟伟荣), and Liang Wei(魏亮)
Department of Physics and Siyuan Laboratory,College of Science and Engineering,Jinan University,Guangzhou 510632,China
1 Introduction
Graphene,as the thinnest material as well as the strongest material in the world,has many excellent performances in mechanical,electronic,thermal,and optical aspects.Recently,the potential applications of graphene with nanopores have aroused much attention,such as seawater desalination,biosensors,ionic sieves of high selectivity and transparency,single-molecule genomic screening devices and so on.[1−5]Simultaneously,a wide range of applications of functionalized graphene have become possible,such as polymer composites,optoelectronic materials and devices and biomedical applications.[6−10]Subnanometer pores can be produced in graphene by employing a focused electron beam.[11]However,it is not feasible to employ this method widely due to its low efficiency and high cost.Since more kinetic energy of heavy ions compared with electrons could be transferred to the target atoms,heavy ions are the most prospective candidate for modifying the morphology of graphene with high efficiency and low cost.In this regard,cluster ion beam is an aggregate of ions which has characteristic performances compared with single ion from the view of not only material science but also ion beam engineering.Both simulation and experiment express that large damage in graphene can be produced by cluster ion beam.[12−14]In the past twenty years,many clusters with special properties have been discovered,e.g.C240,C120,C70,C60,C20,C60@H,C60@He,C60@Ar,C60@Ne,C60@Li,et al.[15−17]Regrettably,the new clusters are only caused by few researchers’attention on the production of graphene nanopores.
In previous works,the mechanisms of the nanopore formation still not be known clearly and the effect of the environmental temperature is always not considered in the process of creating nanopores in graphene.For these reasons,we show our systematic molecular dynamics investigation on the nanopore formation induced by high energy clusters through controlling the environmental temperature,the velocity of clusters and the species of clusters.To understand the process of producing graphene nanopores in fluctuating environment more precisely,we use the simple method of statistical analyses to get its new nature.The microscopic mechanisms of the nanopore formation are observed in details.The results suggest that the cluster ion beam is a good tool to produce graphene nanopores efficiently as well as with low cost.
2 Simulation Methodology
In our molecular dynamics simulations,the clusters contain C70,C60,C60@He,C60@Ar,C60@Ne and C60@Li.The structures of these derivatives of C60 are displayed in Fig.1.The square-shaped graphene is in the xy plane and the z axis is perpendicular to the graphene plane.In the perfect graphene,the length(along the x axis)and the width(along the y axis)of the graphene layer(containing 984 atoms)are 5.08 nm and 5.02 nm,respectively.For studying the effect of defect,we also build a defective graphene by removing a carbon atom in the center of perfect graphene.The outside layer carbon atoms in graphene are fixed during simulations.The center of different clusters is initially placed above the center of the graphene at a large distance(1.5 nm)where there is no interaction between different clusters and graphene.The average velocities of different clusters are perpendicular to the surface of graphene.Additionally,we only consider the energy loss originated from elastic collisions between the cluster and the graphene because nuclear stopping prevails during the ion-graphene interaction process.The electronic stopping,such as ionization and excitation,is not taken into consideration in the calculations since it is not important for the heat conductance of graphene.

Fig.1 (Color online)The structure of C60@M;the red cage is C60,the blue ball in the cage is the atom of M,here M can be Ar,Ne,Li or He.Graphene is on xy plane.
The empirical potential developed by Tersoff and Brenner[18]is a good method of describing the formation and the breaking of carbon-carbon bond in the system,so we employ Tersoff–Brenner potentials to simulate the interaction of carbon atoms in graphene and different clusters.The Lenard–Jones potentials[19]form

are used for van der Waals interactions of gas-gas,gascarbon and metal-carbon interactions.This pair potential has distance and energy parameters obtained with semiempirical combining rules from the Lenard–Jones ε and σ parameters of the carbon atoms and the atoms in C60

where “e”and “C”refer to the atoms in C60 and carbon atoms,respectively.We employ σCC=0.34 nm and εCC=28 K,while parameters of the atoms in C60 are given for some relevant systems in Table 1.[20−21]Bernshtein et al.[22]have used the Lenard–Jones potentials to successfully simulate the behavior of Li in C60,it can accurately describe the interaction between Li and the carbon atom of C60 in our simulations.

Table 1 Parameters of Lenard–Jones potentials for different atoms.
Langevin heat baths are employed to control the temperature of the system.After graphene reaches the state of thermal equilibrium,fullerene and its derivatives will begin to be heated and move to graphene with corresponding velocity.The shape of fullerene and its derivatives be still sphere before bombardment.We integrate the equations of motion by Verlet method.[23]The time step is 0.55 fs.
We use the probability of passing through graphene(Pth)and the probability of the atom in C60 passing through graphene alone(Ped)to describe the bombardment.Here Pthis related to the production efficiency of nanopores.The equations are defined as
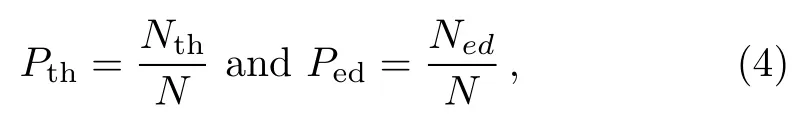
respectively;where N is the frequency of total simulations,Nthand Nedare the frequency of at least one atom of a cluster passing through graphene and the frequency of the atom in C60 passing through graphene alone when all carbon atoms of C60 can not pass through graphene,respectively.
3 Results and Discussion
In our previous studies,[24−25]we have observed that the capability of destroying carbon-carbon bonds in graphene bombarded by C60 obviously increases with the environmental temperature.To analyze the process of passing through graphene when considering thermal fluctuations,we can get its new nature by using simple statistical analyses.
In this paper,the transitional region is defined as the region where the probability of passing through graphene ranges from 0 to 1.For further demonstrating the phenomenon of passing through graphene in the transitional region,we try to control the following factors:the environmental temperature,the species of clusters and the structure of graphene.In our simulations,we will mimic bombardments between graphene and different clusters,which have the same kinetic energy(839.75 eV).Therefore,the corresponding velocity of C60,C60@He,C60@Ne,C60@Ar,C60@Li,and C70 are 15.00 km/s,14.92 km/s,14.59 km/s,14.21 km/s,14.86 km/s and 12.86 km/s,respectively.Usually,even if C60@M have the same temperature,the local thermal fl uctuation can be different.For avoiding the influence of thermal fluctuations,we do 1000 simulations repeatedly to get their average values.The differences between the 1000 simulations are the initial velocity of thermal fluctuation for every atom(carbon and M atom).As displayed in Figs.2(a),the passing probabilities of C60,C60@He,C60@Ne,C60@Ar,and C60@Li obviously increase with the environmental temperature.C60 can easily pass through the defective graphene at the same temperature.However,C70 passes through the graphene difficultly.One can also figure out that C60 implanted with Li can pass through the graphene more easily than C60 contained with Ar.

Fig.2 (Color online)(a)and(b)the probability for passing through graphene(Pth)vs.the temperature and the maximum number of broken bonds in graphene,respectively;(c)and(d)the probability of the atom in C60 pass through graphene when all carbon atoms of C60 can not pass through graphene vs.the temperature and the maximum number of broken bonds(MNB),respectively;(e)the frequency vs.the maximum number of broken bonds in graphene;the length of broken carbon-carbon bond is longer than 0.21 nm[18]in simulations.
The number of broken bonds in graphene was used to de fi ne the extent of damage in graphene.Since the extent of damage in graphene can evolve during bombardment,we can use the maximum number of broken bonds in graphene to measure the extent of damage during bombardment.This method of the maximum number of broken bonds is used for discovering the mechanism of passing through graphene in next simulations.At 500 K,we do 400 00 simulations repeatedly by using different clusters with 839.75 eV.The results are presented in Figs.2(b),2(d)and 2(e). As shown in Figs.2(b)and 2(d),the probability of He in C60 passing through graphene alone decreases with the maximum number of broken bonds quickly.It is illustrated that the behavior of He in C60 is slightly associated with the capability of passing through graphene and then we can consider that the capability of C60@He passing through graphene is almost consistent with C60’s.In Fig.2(b),probabilities of different clusters passing through graphene suddenly increase with the maximum number of broken bonds when the maximum number of broken bonds is larger than 8(as the red line shown in Fig.2(e)).It shows that the clusters need to create a big enough hole for passing through graphene.In Fig.2(e),we can see that all different distributions of the maximum number of broken bonds agree with the normal distribution and probabilities of different clusters passing through graphene strongly depend on their distributions of the maximum number of broken bonds.Therefore,we can understand that,even if the graphene is bombarded by different clusters,the probability of passing through graphene closely relates to the maximum number of broken bonds in graphene.
For further knowing the mechanism of passing through graphene,we still apply the method of the maximum number of broken bonds to discuss it.We simulate C60 with 839.75 eV energy to bombard graphene at 500 K.The initial structure of breaking carbon-carbon bonds affects the next revolution of destroying bonds in graphene greatly.As shown in Figs.3(a)and 3(b),the initial structure of destroying bonds at 101.2 fs was displayed by two differ-ent perspectives.In this simulation,four different areas of breaking bonds near the deformed boundary are generated firstly in the process of bombardment.Simultaneously,the uncertainty of bond-breaking number and location closing to the boundary in the initial structure will lead to the uncertainty of generating nanopores in graphene.But the capability of breaking bonds depends on the velocity of clusters and the strength of carbon-carbon bonds in graphene significantly.As shown in Fig.3(c),the length of carbon-carbon bonds obviously increases with the temperature.High temperature means more energy transmission from C60@M to graphene in the collisions.Then the capability of destroying bonds is enhanced.

Fig.3 (Color online)(a)The top view of C60(with energy 839.75 eV or the velocity of C60 is 15.0 km/s)bombarding graphene at 101.2 fs and the blue dash circle is the boundary of depression;(b)The oblique view of graphene at 101.2 fs after bombardment;the four pink arrows point to four different areas with broken bonds.The environmental temperature is 500 K in both figures.(c)The minimum,mean and maximum lengths of carboncarbon bond in thermal equilibrium vs.temperature.
Based on the initial structure of graphene,the interaction between the graphene and the cluster also plays an important role in the behavior of breaking bonds for C60 passing through graphene.As shown in Figs.4(a),4(b),and 4(c).The three different maximum number of broken bonds are 3,10 and 17,respectively.We can find that the size of small holes created in the initial structure of graphene can constantly evolve under the pressure of C60.The area closing to the center of graphene can be generated small holes by C60 at some time.For this reason,the holes have a higher possibility to form a bigger hole with the adjacent holes for C60 passing through graphene.As displayed in Fig.2(b),the probability of C60 passing through graphene can justify that the possibility of forming a bigger hole increases with the maximum number of broken bonds.
To discover the distribution of the maximum number of broken bonds in graphene bombarded by C60,we do 40000 simulations for more precise.In Figs.4(d)and 4(e),the normal distribution of the maximum number of broken bonds obviously moves from small to large number of broken bonds as the velocity of C60 increasing.All three different kinds of probabilities of passing through graphene depend on the maximum number of broken bonds strongly.However,when the maximum number of broken bonds is between 9 and 25,the probability of C60 with high energy is larger than the one of C60 with low energy clearly.
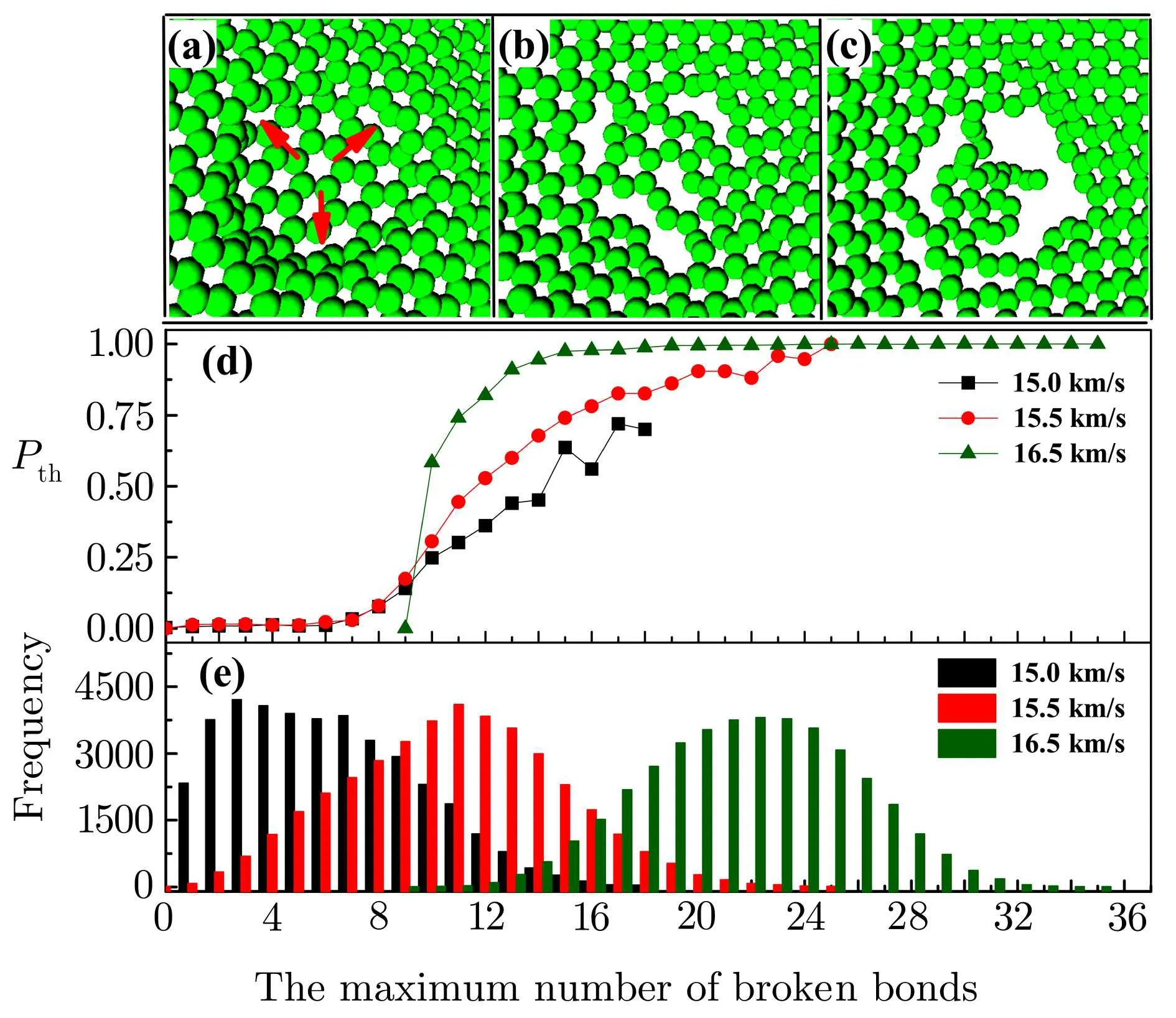
Fig.4 (Color online)Three different maximum numbers of broken bonds selected from 1000 simulations at 500 K are 3(a),10(b)and 17(c),respectively.Three red arrows point to three different areas with broken bonds.The energy of C60 is 839.75 eV.The probability of passing through graphene(d)and the frequency(e)depend on the maximum number of broken bonds.The total frequency of simulations is 40 000 for every average velocity.The temperature is 500 K.
According to the above research,our results not only o ff er insights for further understanding the mechanism of generating nanopore in graphene,but also lead to the potential applications about the functionalization of graphene and the production of nanopores,such as seawater desalination,biosensors,ionic sieves of high selectivity and transparency,single-molecule genomic screening devices,polymer composites,optoelectronic materials and devices,and so on.
4 Conclusion
In conclusion,we have studied the probability of passing through graphene bombarded by different clusters by controlling the environmental temperature,the species of clusters,the incident velocity of clusters and the defect of graphene.In the transitional region of passing through graphene,the temperature of heat baths can obviously influence the probability of passing through graphene significantly.The velocity of clusters changes the passing probability by influencing the energy of clusters.The species of clusters can affect the probability through the deformation of structure during bombardment.The defect of graphene also can obviously improve the probability of passing through graphene due to the instability of carboncarbon bonds near the boundary of defect.Thus,in order to obtain more efficient production of nanopores,we should select the contained atom properly and use right bombard velocity and temperature.Our results may not only offer additional insights for further understanding the mechanism of generating nanopores in graphene,but also lead to some potential applications in the functionalization of graphene and the production of nanopores at low cost and with high efficiency.
Acknowledgments
Our simulations were supported by the high performance computing platform of Jinan University and Siyuan clusters of the physics department.ZWR thanks Y.Xiao at City University of Hong Kong for his contribution in plotting.
References
[1]T.Humplik,J.Lee,S.C.O’Hern,et al.,Nanotechnology 22(2011)292001.
[2]Z.S.Siwy and M.Davenport,Nature Nanotech.5(2010)697.
[3]K.Sint,B.Wang,and P.J.Kr´al,Am.Chem.Soc.130(2008)16448.
[4]S.Garaj,W.Hubbard,A.Reina,et al.,Nature(London)467(2010)190.
[5]G.F.Schneider,S.W.Kowalczyk,V.E.Calado,et al.,Nano Lett.10(2010)3163.
[6]T.Ramanathan,A.A.Abdala,S.Stankovich,et al.,Nature(London)3(2008)327.
[7]S.Stankovich,D.A.Dikin,G.H.B.Dommett,et al.,Nature(London)442(2006)282.
[8]Y.F.Xu,Z.B.Liu,X.L.Zhang,et al.,Adv.Mater 21(2009)1275.
[9]Z.Liu,J.T.Robinson,X.M.Sun,and H.J.Dai,J.Am.Chem.Soc.130(2008)10876.
[10]Y.N.Chan,T.Wong,F.Byrne,M.Kavallaris,and V.Bulmus,Biomacromolecules 9(2008)1826.
[11]M.D.Fischbein and M.Drndi,Appl.Phys.Lett.93(2008)113107.
[12]N.Inui,K.Mochiji,K.Moritani,and N.Nakashima,Appl.Phys.A:Mater.Sci.Process.98(2010)787.
[13]Y.C.Cheng,H.T.Wang,Z.Y.Zhu,et al.,Phys.Rev.B 85(2012)073406.
[14]S.J.Zhao,J.M.Xue,L.Liang,Y.G.Wang,and S.Yan,J.Phys.Chem.C 116(2012)11776.
[15]M.Waiblinger,K.Lips,W.Harneit,A.Weidinger,E.Dietel,and A.Hirsch,Phys.Rev.B 64(2001)159901.
[16]V.Bernshtein and I.Oref,Phys.Rev.A 62(2000)033201.
[17]L.Pang and F.Brisse,J.Phys.Chem.97(1993)8562.
[18]D.W.Brenner,Phys.Rev.B 42(1990)9458.
[19]L.A.Girifalco,M.Hodak,and R.S.Lee,Phys.Rev.B 62(2000)13104.
[20]G.Stan,M.J.Bojan,S.Curtarolo,S.M.Gatica,and M.W.Cole,Phys.Rev.B 62(2000)2173.
[21]T.Halicioglu,G.M.Pound,Physica Status Solidi(a)30(1975)619.
[22]V.Bernshtein and I.Oref,Phys.Rev.A 62(2000)033201.
[23]W.C.Swope,H.C.Andersen,P.H.Berens,and K.R.Wilson,J.Chem.Phys.76(1982)637.
[24]Z.C.Xu and W.R.Zhong,Acta Phys.Sin.8(2014)083401.
[25]Z.C.Xu and W.R.Zhong,Appl.Phys.Lett.104(2014)261907.
 Communications in Theoretical Physics2016年3期
Communications in Theoretical Physics2016年3期
- Communications in Theoretical Physics的其它文章
- Double Wronskian Solution and Soliton Properties of the Nonisospectral BKP Equation∗
- Dynamics of Information Entropies of Atom-Field Entangled States Generated via the Jaynes–Cummings Model
- Temporal Behavior of Rabi Oscillation in Nanomechanical QED System with a Nonlinear Resonator
- Dynamics of Entanglement in Qubit-Qutrit with x-Component of DM Interaction
- Quantum Measurement of Two-Qubit System in Damping Noise Environment∗
- Resonances of Spin-1/2 Fermions in Eddington-Inspired Born-Infeld Gravity∗
