救援通道施工爆破对已建高铁隧道的振动安全分析

夏一鸣，郑明新，胡国平，刘家桦

(华东交通大学岩土与道桥工程研究所，南昌　330013)



救援通道施工爆破对已建高铁隧道的振动安全分析

夏一鸣，郑明新，胡国平，刘家桦

(华东交通大学岩土与道桥工程研究所，南昌330013)

摘要:为确保已建金山顶高铁隧道衬砌结构的安全，有必要在救援通道爆破施工过程中对其开展爆破振动监测。采用TC－4850N无线网络爆破测振仪进行监测，监测结果表明:既有隧道迎爆侧的衬砌结构断面振动最大;基于最小二乘法对监测数据进行回归分析并得到了爆破振动萨道夫斯基经验衰减公式参数;根据公式参数对后续爆破提出了爆破振动控制措施，做到当振动速度超过安全阀值时及时调整爆破参数，取得了较好的效果。

关键词:高铁隧道;振动监测;爆破振动;萨道夫斯基公式

近年来，随着我国高速铁路建设的快速发展，爆破技术在铁路隧道工程的建设中发挥着日益重要的作用。目前，国内隧道爆破开挖多采用钻爆法施工［1］，国内一些学者对隧道爆破振动监测做过许多研究，蔡冻等［2］对野山河隧道进行了爆破振动监测，分析了隧道爆破振动对邻近水电站的影响;宋福［3］对敖包沟隧道进行了爆破振动监测，分析了隧道爆破振动对邻近既有房屋建筑物的影响;刘玉山等［4］对大轩岭隧道进行了爆破振动监测，分析了隧道爆破振动对在建小净距隧道的影响。目前针对邻近大型水电站、邻近既有房屋建筑物、邻近在建隧道的振动安全分析比较多，而对邻近已建高铁隧道的振动安全分析比较少。爆破开挖过程中会产生爆破地震波，地震波产生的振动会对既有邻近高铁隧道产生不利影响，主要表现为爆破振动会造成高铁隧道衬砌结构的不均匀变形，进而可能引起衬砌结构产生裂缝［5］。

因此，在隧道爆破开挖过程中，必须加强对爆破振动的监测与研究，并采取有效措施控制爆破振动的强度。

以金山顶隧道救援通道爆破施工为研究对象，对隧道爆破开挖施工产生的振动进行监测，根据监测得到的数据及爆破振动响应，及时调整和优化新建隧洞施工的爆破设计参数，以保护既有邻近已建高铁隧道免受破坏。

1　工程概况

金山顶隧道救援通道作为金山顶隧道的防灾疏散工程，设计为平导式隧道，位于金山顶隧道进口右侧平行于主洞，与进口段线路右侧的既有综合洞室(正交里程为DK355+224)相接，与主洞净距约为30 m，救援通道与主洞相对位置见图1。平导全长597 m，断面净空尺寸为5 m(宽)×6 m(高)，该平导位于剥蚀中低山区，区内沟谷纵横，植被发育，自然坡度为30°～55°，遂址区地层主要为燕山期花岗岩，中元古界板桥组粉砂质板岩。救援通道隧洞围岩分为3个工程地质段，分别为Ⅱ、Ⅳ、Ⅴ类岩石，具体划分见表1。

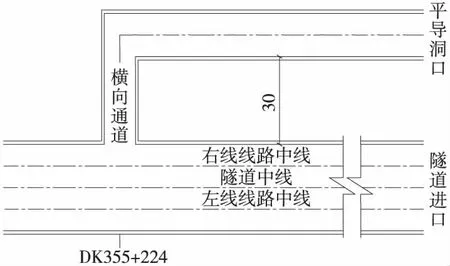
图1　金山顶隧道救援通道平面示意(单位:m)

表1　隧洞围岩分级

金山顶隧道正洞采用复合式衬砌型结构，洞口段小于150 m范围内衬砌采用C35混凝土结合钢筋网型衬砌结构，二次衬砌厚度40～50 cm，混凝土强度35 MPa。洞口段大于150 m范围采用C30素混凝土衬砌结构，二次衬砌厚度35～40 cm。救援通道施工采用人工爆破作业。

2　隧道爆破振动监测

2.1监测仪器及方法

本次隧道爆破振动监测拟采用由TC－4850N无线网络爆破测振仪、Blasting vibration analysis分析软件、计算机、打印机等组成振动监测系统。振动监测采集系统如图2所示，在现场监测过程中，在同一测点布置垂向，切向和径向三个方向速度传感器，传感器用502胶水固定在所需监测部位，再将传感器与爆破测振仪相连，当爆破振动传递到测点时，爆破振动记录仪自动记录信号，然后通过无线网络上传到互联网上专用服务器内，爆破后可利用配套的爆破振动分析软件通过网络将振动信号下载输入到电脑中，并进行分析处理。

图2　振动监测采集系统示意

2.2测点的布置

将传感器布设在既有铁路隧道迎爆侧拱脚上。为了分析振动场的分布情况，了解爆破振动对既有隧道的影响，在爆破源正对既有隧道交叉40～50 m范围内布置3个断面测点，每个测点包括3个速度传感器，分别为垂直地面方向(垂向)、水平径向(其长轴指向爆破源)、水平切向(垂直于径向)，每个观测点同时进行垂直和两个水平方向的观测。

测试工作和隧道爆破开挖作业同时展开，根据测点的布置，测点和爆源之间经历了一个由近及远的过程。监测点平面布置如图3所示，监测点断面布置如图4所示

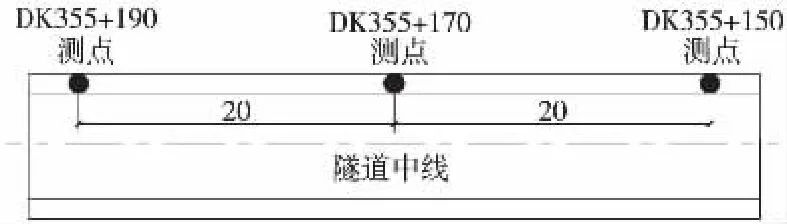
图3　监测点平面布置示意(单位:m)

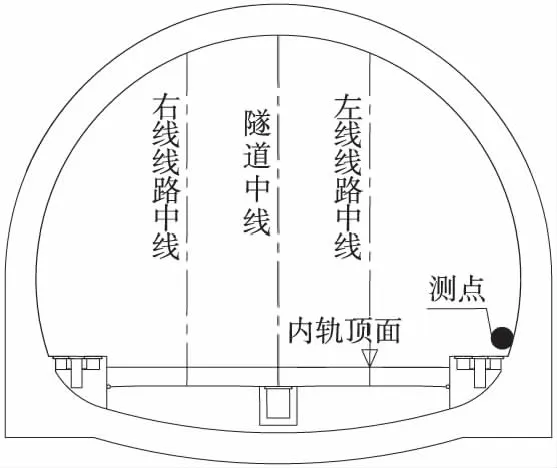
图4　监测点断面布置示意

3　爆破振动监测分析

3.1爆破典型振动波形特征

平导隧道施工采用人工爆破作业，爆破分7段起爆，第1、第2段为掏槽眼爆破，第3～第5段为辅助眼爆破，第6段为底板眼爆破，第7段为周边眼爆破。为了减小爆破对邻近隧道的影响，施工采用了光面爆破，根据围岩特点，并结合断面大小，掏槽眼采用楔形掏槽并分两段起爆，辅助眼应避开节理、裂隙合理选择间距布置，周边眼应合理选择间距并沿开挖轮廓线均匀布置。辅助眼和周边眼孔深均为1.8 m，而且孔底在同一垂直面上，掏槽眼孔深为2.0 m。辅助眼和周边眼单孔装药量分别为0.9 kg和0.36 kg，掏槽眼单孔装药量为1.7～2.0 kg，隧道光面爆破最大单段起爆药量Q 为20.4～24.6 kg。

在典型监测点金山顶隧道DK355+150处得到质点在垂向、水平径向和水平切向3个方向的振动时程曲线如图5所示。由图5可知，振动时程曲线有7个变化点，分别对应7段起爆顺序，最大振速出现在第2段上，即最大振速对应为掏槽眼爆破时刻，应控制掏槽眼的最大装药量。由于采取了合理的微差爆破时间，各段振动波形独立，没有产生明显的振动叠加效应。

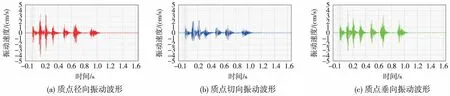
图5　DK355+150测点三向振动波形

3.2爆破振动速度变化特征分析

3.2.1监测控制标准的讨论

振动的物理量一般用质点的振速、加速度、位移和振动频率等表示［6］。用振动的哪些物理量作为衡量爆破振动效应强度的判别标准，在不同的工程实践中，各有侧重，国内外多采用地面质点的振动速度作为衡量爆破强度的判别标准，也有学者研究称爆破振动的主振频率也是一个衡量爆破振动强度的判别标准［7-8］，是一个不可忽略的重要因数，依据我国的《爆破安全规程》［9］(GB 6722—2011)中的规定，也将主振频率纳入了考虑范围。

结合本次工程的实际情况和目前的研究成果及工程经验，根据《爆破安全规程》(GB 6722—2011)的规定，铁路交通隧道安全振动速度标准按10 cm/s＜V＜20 cm/s控制，考虑到金山顶高铁隧道正在试运营，爆破振动过大可能会导致试运营高铁线路路床的不均匀变形及造成线路消防、供电照明和通讯等附属设施的破坏，为了避免以上严重后果的发生而影响试运营高铁的行车安全，为了确保隧道衬砌结构的安全性，规定对既有运营铁路隧道允许的爆破振动速度不宜超过5 cm/s。

3.2.2振动速度变化趋势分析

在DK355+150处进行了13次爆破监测，并运用Blasting vibration analysis分析软件对振动3个方向的波形进行了合成，得到新的波形的矢量振速峰值，具体监测数据见表2，测点质点振速峰值变化趋势如图6所示。

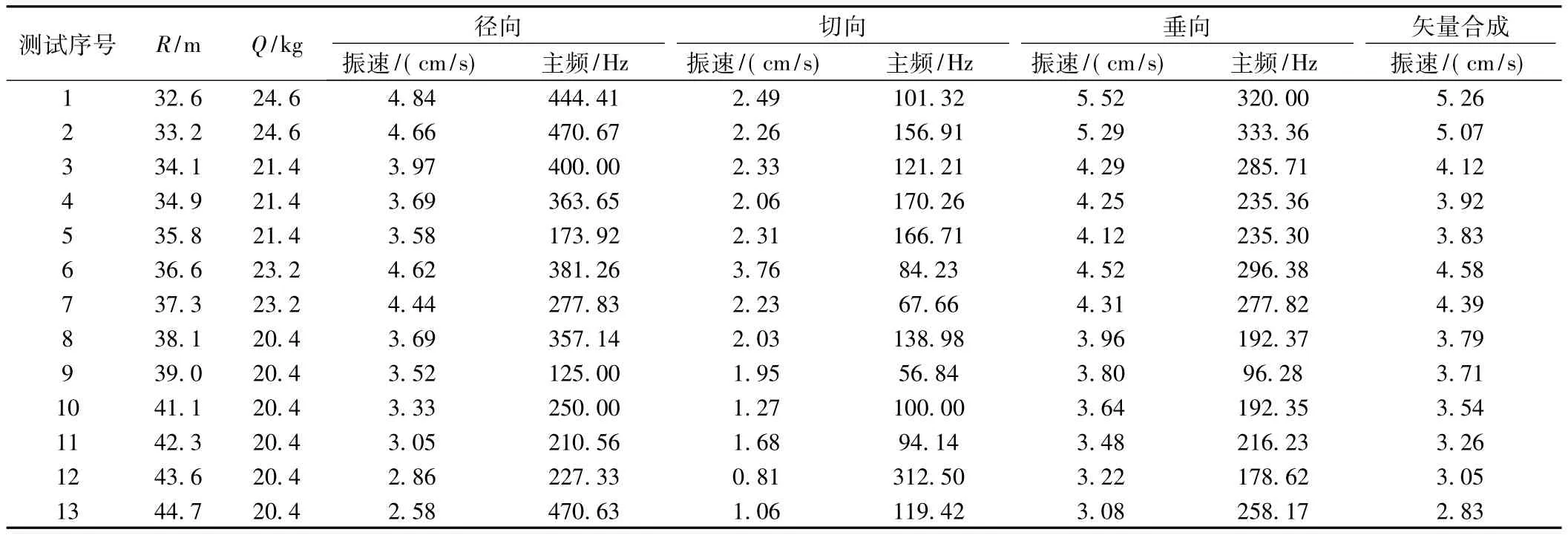
表2　隧道爆破振动监测数据

从表2和图6可以看出。

(1)在桩号为DK355+150测点断面，除了第一次垂向振动速度5.52 cm/s和第二次垂向振速5.29 cm/s，其他次测试质点振动峰值速度均在安全标准5 cm/s内。这可能是因为测点与爆心水平距离较短而且单段最大起爆药量过大造成的，而救援通道是平导式隧道，每次爆破时金山顶隧道必有一个与爆心正对的断面(此断面为最危险断面)，最小水平距离即为测点与爆心的水平距离约为32.6 m。所以只能通过调整单段最大起爆药量或其他措施来控制爆破峰值振速。

(2)测点的垂向和径向的峰值振动速度明显大于切向，而垂向只在第6次和第7次的峰值振动速度小于径向，其他次均大于径向。由此可见，质点朝临空面的峰值振动速度要明显大于其他方向，矢量合成的振速峰值介于垂向和径向之间，这可能是由于同一测点3个方向的振速峰值并非同时达到，具有一定的时间差。因此，在迎爆面垂向是最容易发生破坏也即最危险的方向，径向次之，切向峰值振速明显小于其他方向，在今后类似工程中可只监测垂向和径向振动速度以简化爆破振动监测。

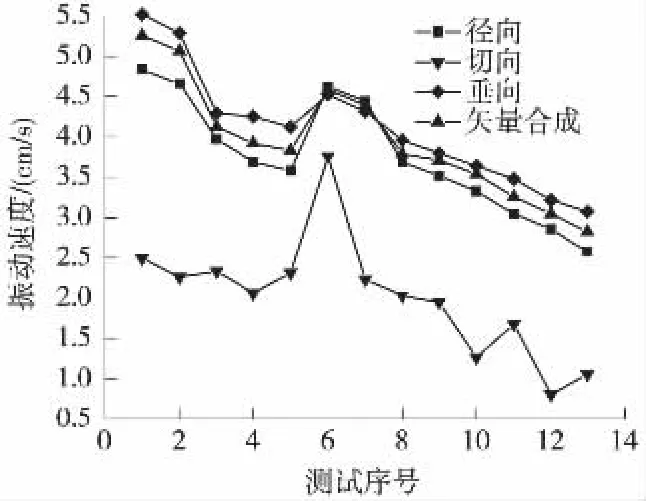
图6　质点振速峰值变化趋势

(3)在单段最大起爆药量不改变的情况下，质点的振速峰值V和爆心距R有明显的对应关系，随着爆破施工的不断推进，测点和爆源经历了一个由近及远的过程，测点质点的振速峰值也随着爆心距的逐渐增大而呈现逐渐衰减的趋势。

(4)振动主频除若干点小于100 Hz以外，其余均大于100 Hz，爆破振动的三向主振频率主要集中在100～400 Hz，属于高频振动。

3.2.3爆破振动衰减公式的回归分析

爆破后会急剧释放能量，并以波动的形式向外传播，引起介质的质点振动，但爆破振动衰减快，依据现有的研究成果，目前国内外一般采用萨道夫斯基经验衰减公式对爆破振动数据进行回归分析［10-12］

式中，V为爆破产生的质点振动速度，cm/s; R为爆源与测点的直线距离，m; Q为爆破单段最大起爆药量，kg; K为与地质条件、围岩特性有关的系数;α为爆破衰减系数。

对式(1)两边取自然对数得

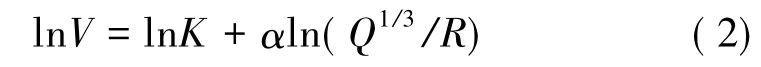
令lnV = y，ln(Q1/3/R) = x，lnK = b，α= m，则将式(2)变换得到一元线性回归公式

利用式(1)～式(3)对表1数据进行最小二乘法回归，得萨道夫斯基经验衰减公式(表3)。

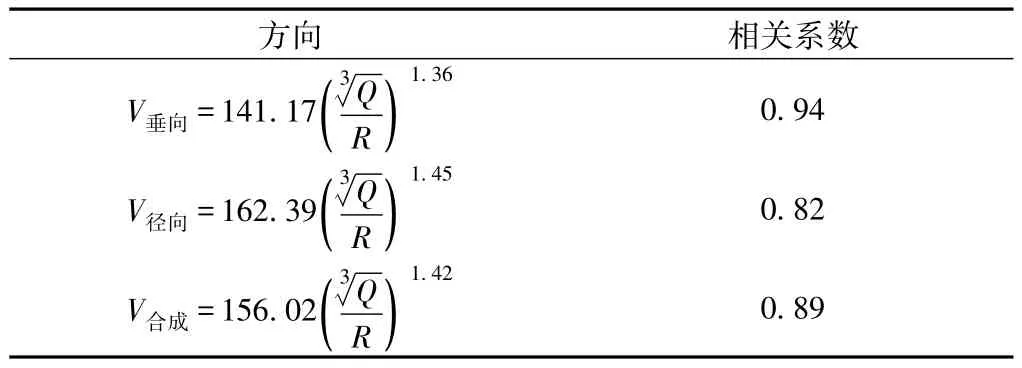
表3　萨道夫斯基经验衰减公式

根据得到的萨道夫斯基经验衰减公式，可以推算确保高铁隧道衬砌结构的爆破振速峰值在安全控制标准以内的单段最大起爆药量

由现场工程实际及安全控制标准可知:Rmin= 32.6 m，Vmax=5 cm/s，代入到表3中的公式进行计算，得到单段最大起爆药量并取其中最小值，得Qmax= 21.5 kg。

4　结论

根据设计要求和《爆破安全规程》(GB 6722—2011)，对金山顶隧道救援通道爆破过程进行了振动监测及分析，通过对监测数据进行分析得到以下结论。

(1)在隧道爆破开挖施工过程中，当最初始监测时爆源正对测点距离爆源最近，产生的峰值振动速度最大;而随着爆源与测点的距离越来越远，对应的峰值振动速度也在逐渐衰减，在单段最大起爆药量不改变的情况下，质点的振速峰值V和爆心距R有明显的对应关系。

(2)爆破振动的三向主振频率主要集中在100～400 Hz，属于高频振动，比既有金山顶高铁隧道衬砌结构的固有频率高很多，因此不会因爆破而产生共振破坏。

(3)基于最小二乘法对监测数据进行回归分析，得到了垂向和径向的萨道夫斯基经验衰减公式，得到在安全控制标准下的单段最大起爆药量为21.5 kg。在后续爆破施工过程中建议将单段最大起爆药量控制在21.5 kg以内效果较好。

参考文献:

［1］李术才，刘斌，孙怀凤，等.隧道施工超前地质预报研究现状及发展趋势［J］.岩石力学与工程学报，2014，33(6):1090-1113.

［2］蔡冻，吴立，梁禹.野山河隧道爆破振动监测与分析［J］.爆破，2009，26(4):89-92.

［3］宋福.敖包沟隧道下穿工程爆破振动监测及减振措施研究［J］.铁道建筑，2013(2):43-45.

［4］刘玉山，陈建平.大轩岭小净距隧道爆破振动监测与分析［J］.爆破，2008，25(2):92-94.

［5］代勇，周建春.天坪岭隧道爆破振动对既有隧道衬砌受力影响监测分析［J］.铁道标准设计，2011(11):97-100.

［6］邓华锋，张国栋，王乐华，等.导流隧洞开挖施工的爆破振动监测与分析［J］.岩土力学，2011，32(3):855-860.

［7］罗忆，卢文波，陈明，等.爆破振动安全判据研究综述［J］.爆破，2010，27(1):14-22.

［8］钟祖良，刘新荣，梁宁慧，等.质点振动速度与主振频率在爆破监测中的应用［J］.重庆建筑大学学报，2006(4):38-41.

［9］中国工程爆破协会.GB 6722—2011爆破安全规程［S］.北京:中国标准出版社，2004.

［10］郭汉超.槐树坪隧道爆破振动监测与控制技术［J］.隧道建设，2006，26(5):47-49，78.

［11］王春梅.小间距隧道爆破对既有隧道振动影响分析［J］.爆破，2013，30(2):84-89.

［12］邓华锋，张国栋，王乐华，等.某水电站导流隧洞开挖爆破振动监测与分析［J］.水电能源科学，2010，28(9):89-92.

Analysis of Vibration Impact Caused by Relief Channel Blasting on Existing High-speed Railway Tunnel

XIA Yi-ming1，ZHENG Ming-xin1，HU Guo-ping1，LIU Jia-hua1
(1.Institute of Bridge＆Road＆Geotechnical Engineering，East China Jiaotong University，Nanchang 330013，China)

Abstract:To ensure the safety of the lining structure of the existing Jin Shan Ding high-speed railway tunnel，it is necessary to monitor blasting operation with TC－4850N wireless blasting monitoring system.The results show that the lining structure section on the blasting side of the existing tunnel vibrates the most.The blasting vibration Sodev's empirical attenuation formula parameters are obtained based on the least squares regression analysis of the monitoring data.And blasting vibration control measures for subsequent blasting operations are proposed in the light of formula parameters so that blasting parameters are adjusted timely once the vibration velocity exceeds the allowable limit.

Key words:High-speed railway tunnel; vibration monitoring; Blasting vibration; Sodev's empirical formula of attenuation

通信作者:郑明新(1966—)，男，教授，主要从事路基与边坡工程研究，E-mail:492001473@ qq.com。

作者简介:夏一鸣(1991—)，男，硕士研究生，E-mail:835866511 @ qq.com。

基金项目:国家自然科学基金项目(51068006) ;江西省高等学校科技落地计划项目(KJLD13036)

收稿日期:2015-07-30;修回日期:2015-08-24

文章编号:1004-2954(2016) 03-0097-04

中图分类号:U458

文献标识码:A

DOI:10.13238/j.issn.1004－2954.2016.03.021