垂直井筒中多相流动的Beggs-Brill压力梯度预测模型的改进

董 勇，李梦霞,，廖锐全，罗 威长江大学信息与数学学院，湖北 荆州教育部油气资源与勘探技术重点实验室(长江大学)，湖北 荆州长江大学石油工程学院，湖北 武汉长江大学地球科学学院，湖北 武汉

垂直井筒中多相流动的Beggs-Brill压力梯度预测模型的改进

董 勇1,2，李梦霞1,2,3，廖锐全2,3，罗 威2,4
1长江大学信息与数学学院，湖北 荆州2教育部油气资源与勘探技术重点实验室(长江大学)，湖北 荆州3长江大学石油工程学院，湖北 武汉4长江大学地球科学学院，湖北 武汉

Beggs-Brill模型是具有代表性的压力梯度计算模型，但存在预测的多相管流压力梯度偏差过大的问题。通过对比Beggs-Brill模型的预测误差与试验设置的参数，认为Beggs-Brill模型预测误差与气液比参数关系密切，建立了Beggs-Brill模型预测误差关于气液比的二次回归模型，并结合该回归模型与Beggs-Brill模型，建立了一种新的压力梯度预测方法，即BBM模型。对90组试验数据的处理结果表明，BBM模型的预测平均相对误差为6.07%，而Beggs-Brill模型的预测平均相对误差为21.56%。以试验中含水率30%、90%的情况为已知数据，采用BBM模型预测含水率60%时的压力梯度，与试验测试压力梯度比较的平均相对误差为15.86%，比Beggs-Brill模型提高了3.7%。BBM模型提高了多相管流压力梯度预测的精度，有助于提高油气井设计和分析的可靠性。

多相流，压力梯度，预测，Beggs-Brill模型

Received: Sep. 20th, 2015; accepted: Jan. 9th, 2016; published: Mar. 15th, 2016

Copyright © 2016 by authors, Yangtze University and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

多相管流压力梯度预测是油气井设计和分析的重要理论基础，前人做了大量工作[1]-[5]。其中，BB模型(Beggs-Brill压力梯度预测模型) [6]能够适用于各种倾斜程度的井筒，得到了广泛应用，是一种具有代表性的压力梯度计算模型。但基于笔者试验测试数据的处理结果表明，BB模型计算的压力梯度与测试压力梯度的平均相对误差21.56%，有必要进一步研究BB模型，建立改进的计算模型。

首先用BB模型计算试验条件下的压力梯度(BB梯度)，利用BB梯度减去测试压力梯度，得到BB预测误差。然后分析BB预测误差和试验条件之间的关系，建立了以气液比为自变量的BB预测误差的二次回归模型(PEM模型)。最后结合PEM和BB模型，得到了一种新的压力梯度预测模型(BBM模型)。计算结果表明，BBM模型更加符合实测压力梯度。

2. BB模型预测效果

试验测试的数据如下：垂直管液流量10～50 m3/d，气液比50～300 m3/m3，测试温度14℃～17℃，介质是空气、5#白油、自来水，压力梯度5.16～28.77 hPa/m，试验数90组(管径75 mm，含水率30%、60%、90%)。粗糙度取0.0002 mm。以含水率30%为例，对比BB模型计算的压降如图1所示。BB模型计算压降值大部分较测试压降值偏大，平均绝对误差为2.69 kPa，平均相对误差为22.1%。

为了改进压力梯度预测模型，继续分析 BB模型预测误差的规律性，将预测误差分别与气流量、液流量、测试压力梯度、BB模型计算压力梯度对比，如图2所示。序号1～5对应设计液流量10 m3/d，序号6～10对应设计液流量15 m3/d，序号11～15对应设计液流量20 m3/d，序号16～20对应设计液流量30 m3/d，序号21～25对应设计液流量40 m3/d，序号26～30对应设计液流量50 m3/d。序号1、6、11、16、21、26对应气液比为50 m3/m3，序号2、7、12、17、22、27对应气液比为100 m3/m3，序号3、9、13、18、23、28对应气液比为150 m3/m3，序号4、9、14、19、24、29对应气液比为200 m3/m3，序号5、10、15、20、25、30对应气液比为300 m3/m3。为了方便对比变量的变化规律，对液流量、气流量分别做了转化，转化关系为液流量乘以10，气流量乘以0.01。

从图2可以看出，当设计液流量相同时，对于不同含水率，预测误差关于气液比的变化规律具有一定的相似性；当含水率固定时，不同的液流量对应的预测误差曲线几何形状差别较大，但基本都具备二次曲线的特征。因此，可以使用二次曲线形式来对预测误差建模。

3. BBM模型

根据前述分析，采用二次函数形式拟合预测误差，所得模型即PEM模型如下：

式中：xi为气液比，m3/m3；yi为预测误差，hPa/m；1,2,---,5i=…；a、b、c为待定拟合系数。BBM模型预测压力梯度为：

式中：VBBM为BBM模型计算的压力梯度值，hPa/m；VBB为BB模型计算的压力梯度值，hPa/m；VPEM为根据预测误差拟合模型计算的压力梯度值，hPa/m。

Figure 1. Comparison between the calculated pressure drop and the test pressure drop图1. BB模型计算压降值与测试压降值的对比

Figure 2. Regularity of prediction error of BB model图2. BB模型预测误差的规律性

BBM预测压力梯度与试验压力梯度的相对误差E定义为：

式中：VE为试验记录的压力梯度，hPa/m。

首先给定含水率和液流量(取决于试验方案)，将给定含水率和液流量对应的气液比、预测偏差值构成二元数组，即(xi, yi)；然后使用最小二乘法，确定出公式(1)中待定系数的值。不同的含水率、液流量组合下的BBM预测偏差曲线的几何形态是不同的，因此公式(1)中的待定系数也不会相同，必须依据试验测试压力梯度数据分别进行拟合来确定系数a、b、c。

BBM模型中，BB模型是完整引用的，对于不同的倾斜角度、含水率、液流量、气液比都是可以使用的。假设已经根据试验数据，确定了试验条件下的PEM模型，但还需要确定其他含水率、液流量、气液比情形下的偏差修正值。笔者采用线性插值方法解决这一问题，并将插值方法得到的压力梯度值称为非试验条件下PEM预测压力梯度。

试验数据中含水率的上限为FWU，下限为FWD；液流量的上限为QLU，下限为QLD；气液比的上限记为RGLU，下限记为RGLD；含水率FW；液流量QL；气液比RGL。

步骤1：若FW、QL、RGL满足，则转步骤2；否则，终止程序，输出：“超出本方法支持的参数范围”。

步骤2：针对试验记录的含水率、液流量数据，选出与FW紧邻的2个含水率，记为FW1、FW2，满足；选出与液流量 QL紧邻的 2个液流量，记为，满足。则记录FW1、QL1对应的PEM模型为f11；FW1、QL2对应的PEM模型为f12；FW2、QL1对应的PEM模型为f21；FW2、QL2对应的PEM模型为f22。

步骤3：根据f11、f12，利用线性插值方法确定含水率为FW1，且液流量为QL时的偏差预测模型，记为f1。

类似，根据f21、f22，确定含水率为FW2，且液流量为QL时的偏差预测模型，记为f2。

步骤4：根据f1、f2，利用线性插值方法确定含水率为FW，且液流量为QL时的偏差预测模型，记为f。

步骤5：将气液比RGL代入公式(6)，得到FW，QL，RGL情形下的BB模型预测误差的拟合值，记为f0；BB模型的预测值减去f0即为BBM模型的预测值。

4. BBM模型的验证

从2个方面对BBM模型进行验证。第1个方面，针对试验设置条件，分析BBM模型的预测精度；第2个方面，以含水率为30%、90%为已知数据，按照BBM模型计算60%含水率情形下的预测压力梯度，将其和测试压力梯度数据对比。

试验设置条件：垂直管，内径75 mm。

对第1个方面验证过程，用公式(3)所示的相对误差衡量，结果如表1所示。90组数据中有14组数据的BBM模型预测相对误差超过10%，最大相对误差34.08%；含水率为30%、60%、90%对应的平均相对误差分别为6.09%、5.97%、6.16%，90组数据的平均相对误差为6.07%。根据文献[6]容易算出，BB模型在含水率为30%、60%、90%对应的预测相对误差分别为22.09%、19.56%、23.03%，平均相对误差为21.56%。因此对于试验设置条件而言，BBM模型优于BB模型。

对第二种验证过程，含水率为30%、90%的数据按照第2节叙述的过程，通过插值的方法计算出含水率60%情形下的预测误差值，按公式(6)得到含水率60%下的BBM压力梯度预测值，由公式(3)计算相对误差(记为非试验条件下BBM预测相对误差)，结果对比如表2所示。30组试验数据中，与试验测试压力梯度比较的平均相对误差为15.86%，但有6组数据BBM模型预测的精度较BB模型差，原因在于含水率间隔过大，加密试验设置的含水率条件，有助于提高 BBM 模型预测精度。但对比平均相对误差，BBM模型的预测精度比BB模型的高3.7%。

Table 1. Prediction of BBM model表1. BBM模型预测效果

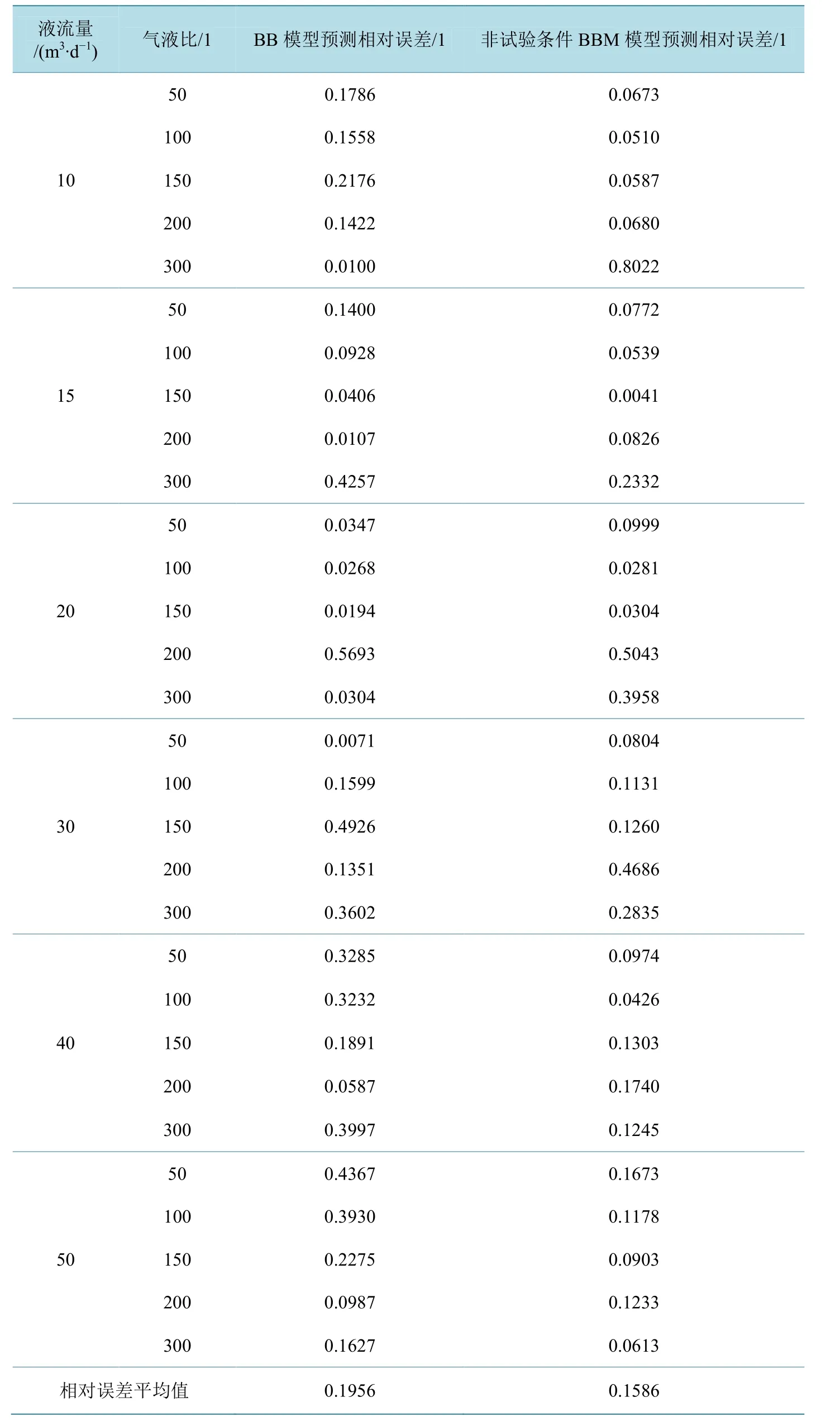
Table 2. Accuracy of predict the pressure gradient between the BBM model and BB model表2. BBM模型预测压力梯度与BB模型预测压力梯度的精度对比

5. 结论

1) 建立Beggs-Brill模型预测误差关于气液比的二次回归模型，结合回归模型与Beggs-Brill模型，建立了一种新的压力梯度预测方法，即BBM模型。

2) BBM模型的预测平均相对误差为6.07%，而Beggs-Brill模型的预测平均相对误差21.56%。

3) 以试验中含水率30%、90%的情况为已知数据，采用BBM模型预测含水率60%时的压力梯度，与试验测试压力梯度比较的平均相对误差为15.86%，比Beggs-Brill模型提高了3.7%。

References)

[1] 周瑞立, 周舰, 罗懿, 等. 低渗产水气藏携液模型研究与应用[J]. 岩性油气藏, 2013, 4(4): 123-128.

[2] 田相雷, 蒋海岩, 岳艳如, 等. 气举排水采气生产规律研究[J]. 断块油气田, 2013, 19(6): 760-763.

[3] 白晓弘, 田伟, 田树宝, 等. 低产积液气井气举排水井筒流动参数优化[J]. 断块油气田, 2014, 21(1): 125-128.

[4] 田云, 王志彬, 李颖川, 等. 速度管排水采气井筒压降模型的评价及优选[J]. 断块油气田, 2015, 22(1): 130-133.

[5] Musaab, M.A. and Ayoub, M.A. (2014) A Comprehensive Study on the Current Pressure Drop Calculation in Multiphase Vertical Wells; Current Trends and Future Prospective. Journal of Applied Sciences, 14, 3162-3171. http://dx.doi.org/10.3923/jas.2014.3162.3171

[6] Beggs, D.H. and Brill, J.P. (1973) A Study of Two-Phase Flow in Inclined Pipes. Journal of Petroleum Technology, 25, Document ID: SPE4007. http://dx.doi.org/10.2118/4007-pa

Modification of Beggs-Brill Pressure Gradient Predicting Model for Multiphase Flow in Vertical Wells

Yong Dong1,2, Mengxia Li1,2,3, Ruiquan Liao2,3, Wei Luo2,4
1School of Information and Mathematics, Yangtze University, Jingzhou Hubei2Key Laboratory of Exploration Technologies for Oil and Gas Resources (Yangtze University), Ministry of Education, Wuhan Hubei3School of Petroleum Engineering, Yangtze University, Wuhan Hubei4School of Geosciences, Yangtze University, Wuhan Hubei

Beggs-Brill Model was a representative one for calculating pressure gradient. There was a large difference between the pressure gradient calculated by Beggs-Brill method and the pressure gradients measured in experiments of multiphase flow in vertical tubing. By comparing the predicting deviations between Beggs-Brill model and experimental apparatus, it was considered that the predicted deviation using Beggs-Brill Model was closely related with the parameters of gas-liquid ratio. And then combining the correlation method with Beggs-Brill Model, a two-regression model based on the deviation of Beggs-Brill Model was established, and in combination with the 2 models, a new pressure gradient predicting method named BBM model was built. The results for 90 groups of experimental data show that the average relative error of BBM method is 6.07% and the one of Beggs-Brill method is 21.56%. Based on the known data with 30% and 90% water contents, BBM model is to predict the pressure gradients at 60% water content, and compared with the BBM gradients with the experimental pressure gradient, the average relative error of BBM modle is 15.86%, which is 3.7% higher than that of Beggs-Brill model. The results show that the BBM model improves the predicting precision of pressure gradient for multiphase flow in vertical wells; it is beneficial for improving the reliability of design and dynamic analysis of oil and gas wells.

Multiphase Flow, Pressure Gradient, Prediction, Beggs-Brill Model

董勇(1980-)，男，博士，讲师，现主要从事演化算法、测井资料解释方面的工作。

2015年9月20日；录用日期：2016年1月9日；发布日期：2016年3月15日

文章引用： 董勇, 李梦霞, 廖锐全, 罗威. 垂直井筒中多相流动的Beggs-Brill压力梯度预测模型的改进[J]. 石油天然气学报, 2016, 38(1): 40-47. http://dx.doi.org/10.12677/jogt.2016.381006

湖北省教育厅科学技术研究项目(B2015449)。