基于MIMO-OFDM系统的改进的广义球解码算法

杨 梅，陈 阳，李满华

安徽工程大学现代教育技术中心，安徽芜湖，241000



自然科学与应用技术研究

基于MIMO-OFDM系统的改进的广义球解码算法

杨 梅，陈 阳，李满华

安徽工程大学现代教育技术中心，安徽芜湖，241000

对MIMO系统中改进的广义球解码算法的研究结果表明，该算法在高信噪比时复杂度较低，并可以实现完全接收分集。并进一步将此算法应用到MIMO-OFDM系统的信号检测中，实现该算法在复杂度和性能两方面的折衷。为了恢复发送端的数据符号，采用基于训练序列的最小二乘时域信道估计方法来获取准确的信道状态信息。改进的广义球解码算法首先引入一个置换矩阵，然后根据信噪比特性来选取初始半径。通过蒙特卡罗仿真法从抗多流干扰能力、抗衰落能力、分集增益和复杂度几个方面来说明改进的广义球解码算法的性能并给出相应的特性曲线。仿真结果表明，该算法在高信噪比时，不仅性能较好而且复杂度较低。

多输入多输出；正交频分复用；广义球解码算法；复杂度

多输入多输出(MIMO，Multiple-inputMultiple-output)在不增加带宽的前提下可以有效地改善系统的容量[1-2]及其性能，从而显著地提高网络的覆盖范围和实现传输的高度可靠性[3]。然而，当高速传输数据时，环境的多径使MIMO信道成为频率选择性信道。正交频分复用(OFDM，OrthogonalFrequencyDivisionMultiplexing)将频率选择性多径衰落信道转化为频域内的平坦信道，减小了多径衰落的影响。因此，OFDM和MIMO技术的有效结合被普遍认为是未来宽带无线通信的有效解决方案之一。为了提高数据传输速率，接收机需要准确估计信道的状态信息。然而，在多天线OFDM中，来自不同天线的不同信号同时发送，接收信号是这些信号的叠加。由于各个天线的信号间存在一定的相关性，从而导致多流干扰(MSI，Multi-StreamInterference)[4]。这对信号检测提出了挑战[5]。因此，在接收端设计复杂度低且性能好的信号检测算法是体现MIMO-OFDM系统优越性的关键。从以前的研究可知[6]，MIMO系统中改进的广义球解码算法不但性能较好，而且可以实现完全接收分集。为此，本文将此种次优检测算法应用到MIMO-OFDM系统的信号检测中，从而满足不同的服务质量要求。

1 MIMO-OFDM系统模型

MIMO-OFDM通信系统的原理框图如图1所示。假设系统有Nt根发射天线数，Nr根接收天线数，且Nt≤Nr。图1中，接收信号为发送信号和噪声的叠加[7-8]，即：

(1)

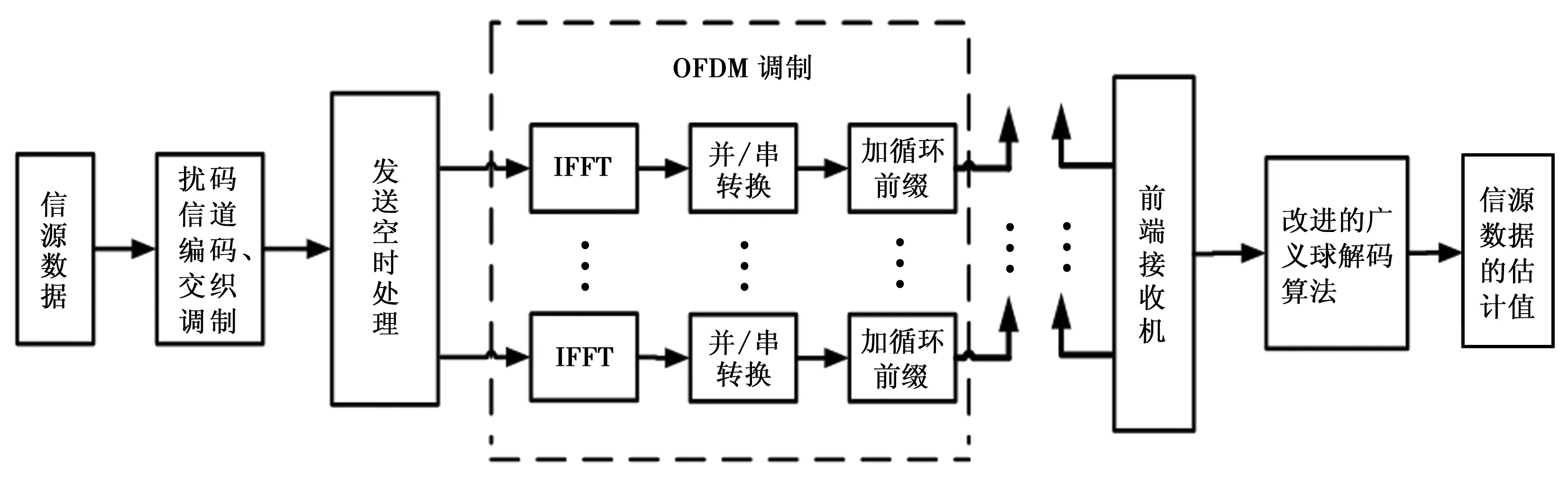
图1 MIMO-OFDM系统改进的广义球解码算法原理框图

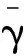
(2)

且[H[k]]uv=huv[k](u=1,…,Nt,v=1,…,Nr)是第k个子载波第u根发送天线和第v根接收天线之间的信道时域冲激响应，即：

(3)

式中,L是NrNt个SISO(单输入单输出)信道的最大时延，guv[l],l=0,1,…,L-1是频率选择MIMO信道中，第u根发送天线和第v根接收天线的信道脉冲响应。

MIMO-OFDM系统第k个子载波的接收信号为：

(k=0,1,…,Nc-1)

(4)

式中，y[k]=[y1[k],y2[k],…,yNr[k]]T，H[k]中的每个元素都满足(2)，且发送信号x[k]=[x1[k],x2[k],…,xNt[k]]T，噪声n[k]=[n1[k],n2[k],…,nNr[k]]T。

2 改进的广义球解码算法

由上文可知，改进的广义球解码算法在MIMO系统中是通过转换变为搜索格中最近格点的问题。由于格是在实域中定义的，所以首先要将式(1)描述的MIMO-OFDM复数域系统转换成实数域系统：

(5)

首先，等式(6)的两边左乘矩阵KT，即可得到：

(6)

然后，等式(6)两边左乘矩阵P(矩阵P满足PTP=I)，得到：

(7)

其次，MIMO-OFDM系统中改进的广义球解码算法初始半径的选取和MIMO系统相同，也是根据信噪比的特性来选取的，即按照信噪比的特性[10]来选择初始半径c，即c=2σ2αNT。

最后，在已知输入γ：接收信号Y′、初始半径c、信道估计出的信道参数K以及由调制方式决定的调制子集的情况下，搜索满足下式的网格点：

(8)

式中，S表示Zn内考虑的网格点。

算法如同MIMO系统类似，不同之处在于表示算法的输入、搜索半径、椭圆上下界以及算法输出等的变量不同。这里不再详述，具体参照相关文献[11-12]。

3 仿真结果和性能分析

以下运用MATLAB软件仿真对提出的算法从抗多流干扰能力、抗衰落能力、复杂度和分集增益几个方面进行性能分析。假设最大时延扩展为75 ns的瑞利衰落信道，假设接收端已知信道信息完全同步，为了讨论问题的方便，避免交织对算法的影响，在仿真设计中不采用交织，卷积编码速率为1/2，系统带宽为20 MHz，每个OFDM符号有64个子载波。

3.1 抗多流干扰能力

图2是采用4根发送天线、5根接收天线的情况下，在不完全信道估计下，改进的广义球解码算法在不同调制方式下的性能比较。从图2可以看出，4QAM性能最好，64QAM性能最差，其算法的误码率随调制阶数的增大而增大。因为高阶调制(如64QAM)比低阶调制(如4QAM)更容易受到符号间干扰和码间干扰的影响，所以高阶调制的误码率较高。

图2 改进的广义球解码算法在不同调制方式下的性能比较图

3.2 抗衰落能力

图3 改进的广义球解码算法在两种信道估计下的性能比较图

一个有4根发送天线、5根接收天线的MIMO-OFDM系统，采用64QAM调制。当能完全估计信道状态信息和不完全(基于LS)估计信道状态信息时，改进的广义球解码算法的误码率和信噪比的关系曲线如图3所示。从图3可以看出，基于LS信道估计与完全信道估计相比，性能约有2 dB的差异，但在实际系统中，完全信道估计一般很难实现。

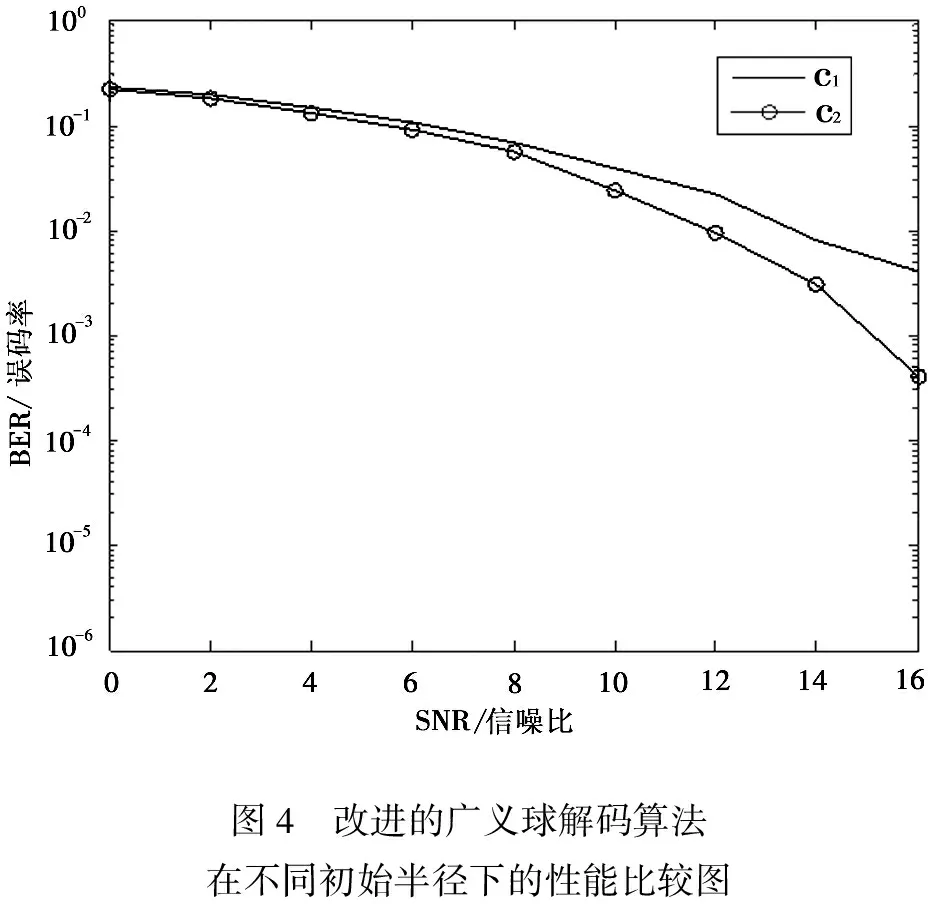
图4 改进的广义球解码算法在不同初始半径下的性能比较图

3.3 分集增益

根据文献[13]中分集增益的公式，可以得出改进的广义球解码算法的分集增益(表1)。表1的仿真条件为：假设不完全信道估计下，一个有5个发射机和6个接收机的MIMO-OFDM系统，且每个发射机均采用4QAM调制。

由表1可以看出，随着信噪比的增大，改进的广义球解码算法的分集增益趋于6，所以可以实现完全接收分集。

表1 改进的广义球解码算法的分集增益

3.4 复杂度

一般来说算法性能越好，其算法复杂度必定越高。下面按照文献[14]中计算复杂度的公式来计算复杂度，并通过实验数据来分析说明，具体分析见表2。该表的仿真实验条件为：假设不完全信道估计，一个有2个发射机、3个接收机的MIMO-OFDM系统，每个发射机均采用4QAM调制。

表2 改进的广义球解码算法不同初始半径的比较

由表2可以看出，信噪比在0到20之间时，c1总是小于c2，所以改进的广义球解码算法的复杂度相对较高。但是，当SNR大于20 dB时，c1大于c2，且在SNR大于40 dB时，c1远远大于c2。所以算法的复杂度降低了。由此可以得出，改进的广义球解码算法在解决高信噪比时，复杂度较低。

4 结 语

本文将改进的广义球解码算法应用到MIMO-OFDM系统，获得了比较满意的结果。该算法是在以接收信号点为圆心、一定半径的空间内搜索欧氏距离最近的星座点。通过选择合适的搜索半径来降低复杂度，但又不过多地牺牲算法的检测性能。此算法首先引入一个置换矩阵，然后根据信噪比特性来选取初始半径，分析了这种算法处理接收信号、获得发送信号估计值的基本理论和工作原理。由分析结果和仿真实验表明，改进的广义球解码算法在高信噪比时，不仅性能较好而且复杂度较低,且能够实现完全接收分集。

[1]Bessai H J.MIMO Signals and Systems[M].New York:Springer,2005:1-11

[2]Oestges C,Clerckx B.MIMO wireless communications:from real-world propagation to space-time code design[M].London:academic press,2007:119-126

[3]Yang H.A road to future broadband wireless access:MIMO-OFDM-Based air interface[J].IEEE Communications Magazine,2005,43(1):53-60

[4]Sampath H,Talwar S,Tellado J,et al.A fourth-generation MIMO-OFDM broadb and wireless system:Design,performance,and field trial results[J].IEEE Communications Magazine,2002,40(9):143-149

[5]Damen G,Chleif A,Belfiore J.Lattice Code Decoder for Space-Time Codes[J].IEEE Communication Letters,2000(4):161-163

[6]杨梅，陈阳，李满华．一种基于MIMO系统的改进广义球解码算法[J]．长江大学学报:自然科学版，2016，13(1)：7-11

[7]Paulraj A,Nabar R,Gore D.Introduction to space-time wireless communications[M].3rd ed.Cambridge:cambridge university press,2003:182-188

[8]Che H,Nassereddine A,Nikookar H,et al.Another Parameter Representing QoS Gain of MIMO Systems[C]//Amsterdam:Institute of Electrical and Electronics Engineers,2004:89-92

[9]Li Y,Seshadri N,Ariyavisitakul S.Channel estimation for OFDM systems with transmitter diversity in Mobile wireless channels[J].IEEE Journal on Selected Areas in Communications,1999,17(3):461-471

[10]Varanasi M K.Decision Feedback Multiuser Detection:A Systematic Approach [J].IEEE Trans Info Theory,1999,45:219-240

[11]Damen M O.Joint coding/decoding in a multiple access system,application to Mobile communications[D].Paris:ENST de Paris,1999:119-132

[12]Yang Z-k,Liu C,HE J-h.A new approach for fast generalized sphere decoding in MIMO systems[J].IEEE Signal Processing Lett,2005,12(1):41-44

[13]Fincke U,Pohst M.Improved Methods for Calculating Vectorsof Short Length in a Lattice,Includinga Complexity Analysis [J].Mathematics of Computation,1985,44:463-471

[14]Zheng L Z,David N,Tse C.Diversity and Multiplexing:A Fundamental Tradeoff in Multiple-Antenna Channels [J].IEEE Trans Info Theory,2003,49:1073-1096

(责任编辑：汪材印)

10.3969/j.issn.1673-2006.2016.06.026

2016-03-16

安徽省教育厅自然科学研究一般项目“MIMO-OFDM通信系统信号的盲量子进化球面检测算法的初步研究”(TSKJ2014B03)。

杨梅(1983-)，女，安徽宿州人，硕士，工程师，主要研究方向：电子技术和通信信号处理。

TN929.5

A

1673-2006(2016)06-0095-04