一种基于Voronoi图的多晶体有限元建模方法

郑战光，汪兆亮，冯　强，袁　帅，王佳祥

(1.广西大学机械工程学院, 广西南宁530004；2.广西制造系统与先进制造技术重点实验室， 广西南宁530004)



一种基于Voronoi图的多晶体有限元建模方法

郑战光1,2，汪兆亮1，冯强1，袁帅1，王佳祥1

(1.广西大学机械工程学院, 广西南宁530004；2.广西制造系统与先进制造技术重点实验室， 广西南宁530004)

摘要:建立多晶体的细观有限元模型是研究多晶体材料局部塑性变形不均匀性的前提与基础，为了灵活地构建高可靠度的材料微结构模型，在前人研究成果的基础上提出一种基于Voronoi图并结合单元编号区域排布特点，能直接根据模型中得到的单元编号顺序依次求取单元形心坐标的构图方法就显得极为关键。该方法首先是生成特定平面或空间域里的随机点与Voronoi图基本信息，再结合单元编号区域排布特点依次直接求取中心点坐标，接着判断单元归属于距离最近的晶核所在的晶粒内，并将所得晶粒编号及单元编号以set集合形式添加到INP文件的Part部分，进而得到Voronoi多晶体有限元模型，最后以构建含10个晶粒的二维和三维多晶体模型为例和文献对比分析来进行实现与验证。结果显示：该方法可以依据单元编号区域排布特点直接得到单元编号且更加容易实现依次求取单元形心坐标，并在一定程度上降低了单元形心坐标处理的数据量和单元归属判断的难度，通过对比分析该方法建立的模型精度更接近于文献中的精确模型，它们之间的最大偏差仅为25.47 MPa，较对比文献的简化模型最小偏差还要低0.07 MPa。表明该方法可为研究人员快速构建多晶材料的Voronoi细观有限元模型提供一定的技术参考。

关键词:Vonronoi图；多晶体建模；晶体塑性；有限元；

0引言

随着计算几何学和计算机图形技术的快速发展以及国内外在细观尺度下研究金属不均匀变形与内部晶粒演变之间关系等热点问题的兴起，学者们纷纷提出了一些方法来模拟多晶体位相分布的方法。目前应用较多的方法有Voronoi图方法、蒙特卡罗方法和元胞自动机方法等，其中，Voronoi图方法可以与有限元方法相耦合来建立多晶有限元模型，所建立的模型能灵活地分析不同材料微结构演变的物理机制，而且存储数据少，计算速度快，因此Voronoi图方法在国内外得到了广泛的应用[1-5]。基于Voronoi图的多晶体有限元建模常采用如下两类方法：①先生成Voronoi晶胞的基本信息，将其按一定顺序保存为数据文件，然后通过Python脚本语言对ABAQUS进行二次开发就可以生成Voronoi多晶材料的细观有限元模型。如司良英等[6]通过先在MATLAB生成Voronoi晶胞，将其按一定的顺序保存为数据文件，然后在ABAQUS/CAE中用其与Python接口将其读入，调用ABAQUS/CAE中Python程序接口，最终生成所需的有限元多晶几何模型；樊黎霞等[7]通过MATLAB里的Voronoi函数把各晶粒的顶点和晶粒顺序号存储到文件中，通过Python语言读入到ABAQUS有限元软件建立的几何模型，按照顺序依次连接晶粒的各顶点，然后采用分割面的功能生成Voronoi多晶有限元几何模型；张丰果等[8]先在区域R内生成Voronoi晶胞的随机种子点，接着对区域R预先划分的每一个网格单元采用最短距离的方法判断其归属于哪个晶粒，将得到的基本信息添加到Python脚本文件，最终建立了基于Voronoi图的粗糙多晶模型；汪凯[9]采用Python脚本语言getNodes命令，先获得每个单元所包含的节点坐标，然后计算每个单元形心与所有种子点的距离，通过排序函数getMin得到最小数的编号，就将该单元放到该种子所对应的集合(晶粒)中，即可得到三维Voronoi多晶简化模型。②先生成Voronoi图的基本信息，再将获得的Voronoi几何信息添加到ABAQUS预先生成的单晶模型INP文件中，最终得到多晶体塑性变形有限元模型。如伊兴华[10]利用Voronoi图表技术，先通过MATLAB编程得到多晶的拓扑信息，然后在ABAQUS软件的前处理模块CAE中建立模型的几何信息部分，并结合MATLAB程序得到的Voronoi信息，最终得到晶体塑性模型的ABAQUS输入文件。

上述两类方法在获取Voronoi图的基本信息时均涉及到对单元形心坐标的处理，这样因选择的参考坐标系不同或因直接采用先求单元节点坐标、再求单元形心坐标的方法均会加大数据的处理量，同时也会对后面单元归属的判断增加一定的难度。据此，本文提出一种基于Voronoi图并结合单元编号区域排布特点，直接根据模型中得到的单元编号顺序，并依次求取单元形心坐标的构图方法。该方法是先生成特定平面或空间域里的随机点与Voronoi图基本信息，接着结合单元编号区域排布特点依次直接求取中心点坐标，判断单元归属，将所得晶粒编号及单元编号以set集合形式添加到ABAQUS的INP文件Part部分，进而得到Voronoi多晶体有限元模型。

1Voronoi多晶体模型的构建

金属材料晶粒实际上大小不一、形状各不相同，在传统的晶体塑性有限元模拟中常用一个规则的多面实体单元代表一个晶粒(单胞)，这种模型假设无法真实描述材料的微观织构，且不能够反应晶体内部的不均性变形[11]。鉴于Voronoi图技术算法已经非常成熟，在MATLAB的Multi-Parametric Toolbox(MPT)工具箱有专门构建Voronoi图二维与多维的函数。但是如何通过MATLAB-MPT工具箱并结合MATLAB编程得到带有边界限制的完整的二维与三维Voronoi图的几何拓扑信息是建立Voronoi多晶有限元模型最为关键的技术难题；同时晶粒数目较多时，如何将处理好的晶粒编号及所包含的单元信息以建立集合的方式写进INP文件中来获得Voronoi多晶有限元模型也需要技术攻关。为此，本文提出一种基于Voronoi图并结合单元编号区域排布特点，直接根据模型中得到的单元编号顺序，并依次求取单元形心坐标的构图方法，为研究人员在ABAQUS平台下进行Voronoi多晶材料的细观有限元模型的建模提供一些技术参考。

1.1Voronoi图的简介

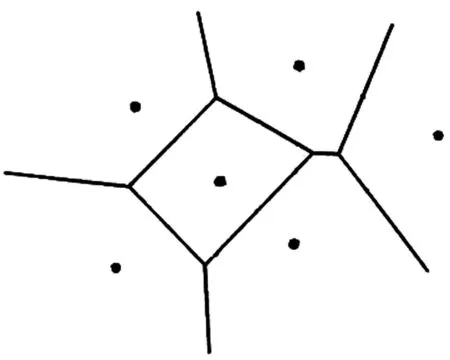
图1　Voronoi方法的原理图Fig.1　The principle diagram of Voronoi method

Voronoi方法广泛应用于气象学、地理学、图像处理、结晶学、微观结构模拟和城市规划等领域[1-6]。它是由俄罗斯数学家Voronoi于1908年提出了n维Voronoi图的定义,其主要思路是通过临近原则将n维空间体进行剖分，使其成为无数多面体的集合体(如二维情况即将空间平面剖分成无数多边形的集合体)，每个多面体事实上是依靠其内部的一个核心点控制生成的，每个核心点的影响域是由至该点的距离最近的点组成的集合(临近原则)，该核心点的影响域即构成相应的多面体[1-6]。生成Voronoi图的初始点称作Voronoi图的发生元。从定义中可以看出，Voronoi图就是基于距离最近原则对空间划分而成的多边形(二维)或多面体(三维)图形集合，每个多边形内部任意一点到该多边形对应种子的距离都比到其他种子点的距离近，其主要描述了空间点的邻近区域或者影响区域的边界。Voronoi方法的原理图如图1所示。

1.2二维Voronoi模型的构图方法

按照如图1所示的Voronoi方法的原理图，在MATLAB中先生成种子点的随机坐标，依次求解每个单元的中心点坐标到每个种子点(晶核)的距离，并将该单元归属到距离最短的晶核所在的晶粒内，从而得到每个晶粒的完整拓扑信息，接着将得到的每一个晶粒编号及所对应的单元编号，以set集合的形式写进ABAQUS的INP文件中Part部分最终实现整个二维Voronoi多晶模型的建立。

二维Voronoi多晶模型完整建模的程序流程图如图2所示，具体实施步骤如下：

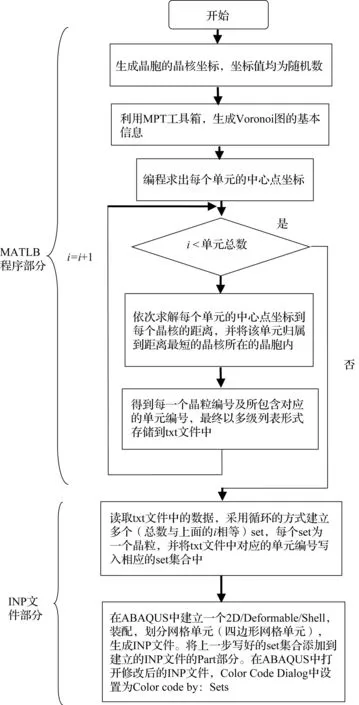
图2　二维Voronoi多晶模型建立的流程图

①先在特定空间剖分得到晶核坐标的随机数，利用MATLAB中MPT工具箱提供的mpt_voronoi命令，生成所需大小和晶粒数的Voronoi图基本信息并画出二维模型图。

②结合单元编号区域排布特点，尤其是单元区域分布及编号顺序，编程直接求取每一个单元的中心点坐标，单元是通过在ABAQUS/CAE中建立一个与二维模型图相同尺寸的2D/Deformable/Shell模型划分网格之后所得，单元具体信息可以在生成的INP文件中查看。

③根据ABAQUS/CAE中划分网格后实体模型的单元空间排布特点，依次求解每个单元的中心点坐标到每个晶核的距离，并将该单元归属到距离最短的晶核所在的晶胞内。

④将得到的每一个晶粒编号及其对应的所有单元编号，最终以多级列表形式保存到txt文件中。

通过以上MATLAB编程，本文仅得到的是二维Voronoi图完整的拓扑信息。下面还需要在ABAQUS的INP文件中的Part部分编写多个set集合，其中每个set集合为一个晶粒，将txt文件中对应的单元编号依次写入相应的set集合实现建模。利用INP文件进行二维模型建立的过程如下：

①在ABAQUS/CAE中建立一个2D/Deformable/Shell，装配，划分网格单元(四边形网格单元)，并在Job模块中生成INP文件。

②将上一步写好的set集合添加到建立的INP文件中的Part部分。在ABAQUS中打开修改后的INP文件，并在Color Code Dialog中设置为Color code by：Sets。

1.3三维Voronoi模型的构图方法

以上建立的二维Voronoi模型中每个晶粒为一个多边形，所以二维Voronoi多晶模型的几何拓扑构图方法相对简单，而三维模型是一个多面体，并且金属多晶材料是由多个不规则晶粒的空间构成，因而其拓扑结构比二维情况要复杂得多，更为糟糕的是在三维模型下单元按晶粒分组和拓扑数据处理在MATLAB中均没有函数直接实现。为此，本文紧紧围绕Voronoi图是由一组由连接两邻点直线的垂直平分线组成的连续多边形，并根据ABAQUS/CAE中划分网格后实体模型的单元编号空间排布特点，在MATLAB中编程依次求解每个单元的中心点坐标到每个晶核的距离，并将该单元归属到距离最短的晶核所在的晶胞内，从而得到每个晶粒的完整拓扑信息，接着将得到的每一个晶粒编号及对应的所有单元编号，以set集合的形式写入ABAQUS的INP文件中的Part部分，最终实现整个三维Voronoi模型的建立。

三维Voronoi多晶模型完整建模的程序流程图如图3所示，具体实施步骤如下：

①先在特定空间剖分得到晶核坐标的随机数，利用MATLAB中MPT工具箱提供的 mpt_voronoi命令，生成所需大小和晶粒数的Voronoi图基本信息并画出三维模型图。

②结合单元编号区域排布特点，尤其是单元区域分布及单元编号顺序，编程直接求取每一个单元的中心点坐标，单元是通过在ABAQUS/CAE中建立的一个与三维模型图相同尺寸的3D/Deformable/Shell模型划分网格后所得，单元具体信息可以在生成的INP文件中查看。

③根据ABAQUS/CAE中划分网格后实体模型的单元空间排布特点，依次求取每个单元的中心点坐标到每个晶核的距离，并将该单元归属到距离最短的晶核所在的晶胞内。

④将上一步得到的每一个晶粒编号及其对应的所有单元编号，最终以多级列表形式存储到txt文件中，以供后续修改INP文件的调用。

通过以上MATLAB编程，本文仅得到了三维Voronoi图完整的拓扑信息。下面还需要在ABAQUS的INP文件中Part部分编写多个set集合，每个set集合为一个晶粒，并将txt文件中对应的单元编号写入相应的set集合实现建模。利用INP文件进行三维模型建立的过程如下：

①在ABAQUS/CAE中建立一个3D/Deformable/Shell，装配，划分网格单元(四边形网格单元)，并在Job模块中生成INP文件。

②将上一步写好的set集合添加到建立的INP文件中的Part部分。在ABAQUS中打开修改后的INP文件，并在Color Code Dialog中设置为Color code by：Sets。

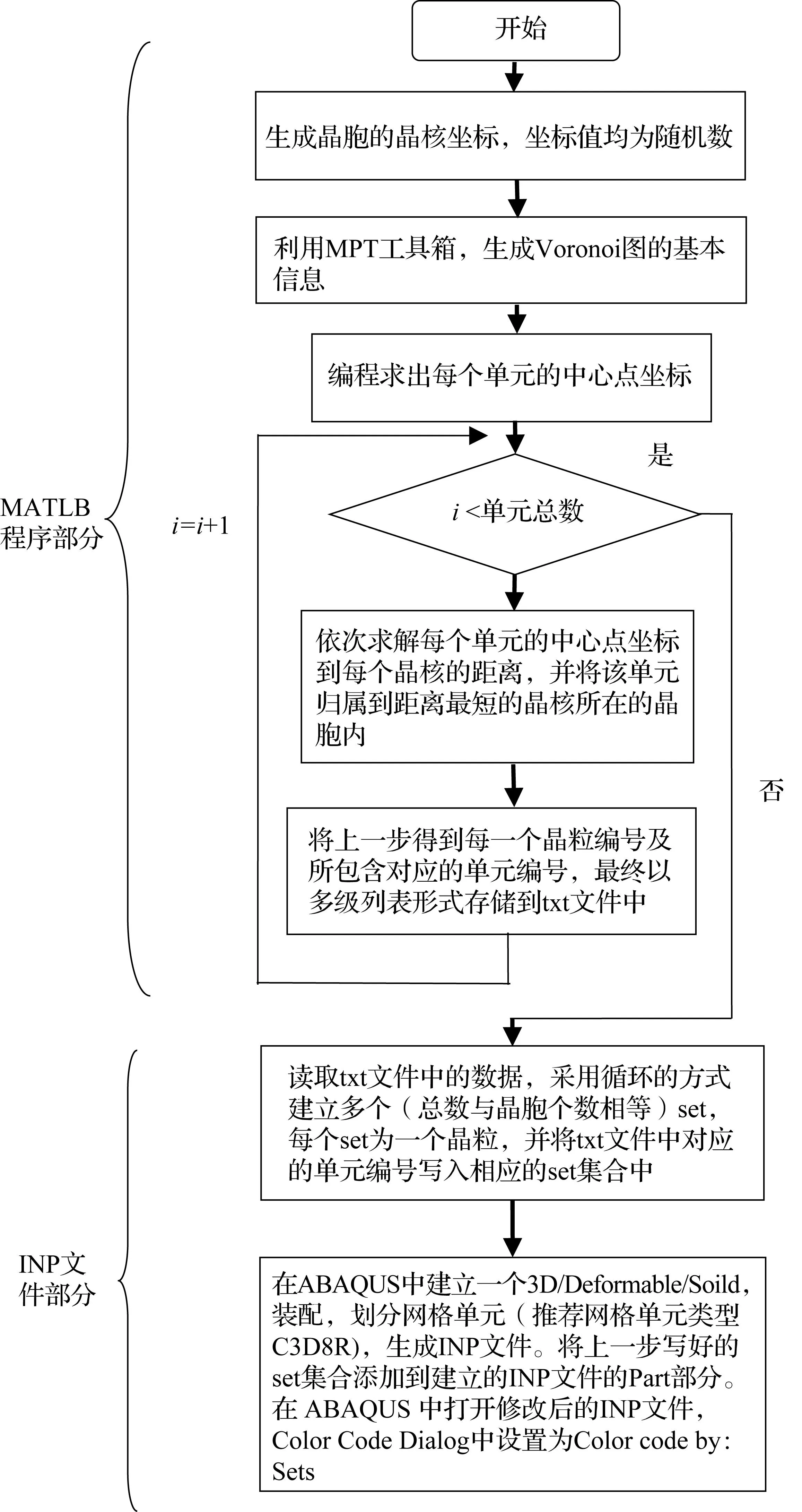
图3　三维Voronoi多晶模型建立的流程图

2案例分析

鉴于工程中使用最多的是金属材料，而金属材料又大多是晶粒的集合，即多晶体；并且多晶体材料的微观组织结构复杂，因此在建立Voronoi多晶有限元模型时，很难完全真实地反映出晶粒的各个方面的特征，必须对其进行合理假设[12-13]。本文考虑到多晶材料在晶粒大小、形状上均具有很大随机性的特点，基于Voronoi图原理通过MATLAB-MPT工具箱结合MATLAB编程，分别得到带有边界限制的完整的二维、三维Voronoi图几何拓扑信息，并以建立集合的方式将处理好的晶粒编号及其包含的所有单元信息写入ABAQUS的INP文件中实现模型的建立。该模型不仅能够十分形象真实地反映实际多晶体的构成形态，而且还为后续的材料参数、取向的赋予、实施不同类型的加载等[14]以编写INP文件的方式实现及其细观尺度下金属变形与内部晶粒演变的关系分析提供前期的数据准备。下面分别以二维和三维多晶体有限元模型构建为例对本文所提出的方法进行实现与验证。

2.1建立二维多晶体有限元模型

为了实现多晶体晶粒呈不同形态与尺寸大小的二维Voronoi图，根据图2所示的二维Voronoi多晶模型建立的流程图，本文首先在MATLAB中随机生成任意分布类型的种子点，再根据随机种子点生成二维Voronoi图。MATLAB中的二维Voronoi图如图4所示。

通过MATLAB编程虽然得到了二维Voronoi图完整的拓扑信息，并实现了二维Voronoi图，但它仅仅是带有二维Voronoi图完整拓扑信息的多晶体示意图，并不是一个带有完整边界限制的二维Voronoi多晶体有限元模型。同样，根据图2所示流程图的INP文件部分的分析流程，本文以建立的一个包含10个晶粒的二维多晶体有限元模型为例，其多晶体晶粒的相关参数与图4 所示在MATLAB中生成的二维Voronoi图尺寸及晶粒位置、个数均相同，并通过编写ABAQUS的INP文件的形式进行实现，最终结果如图5所示。

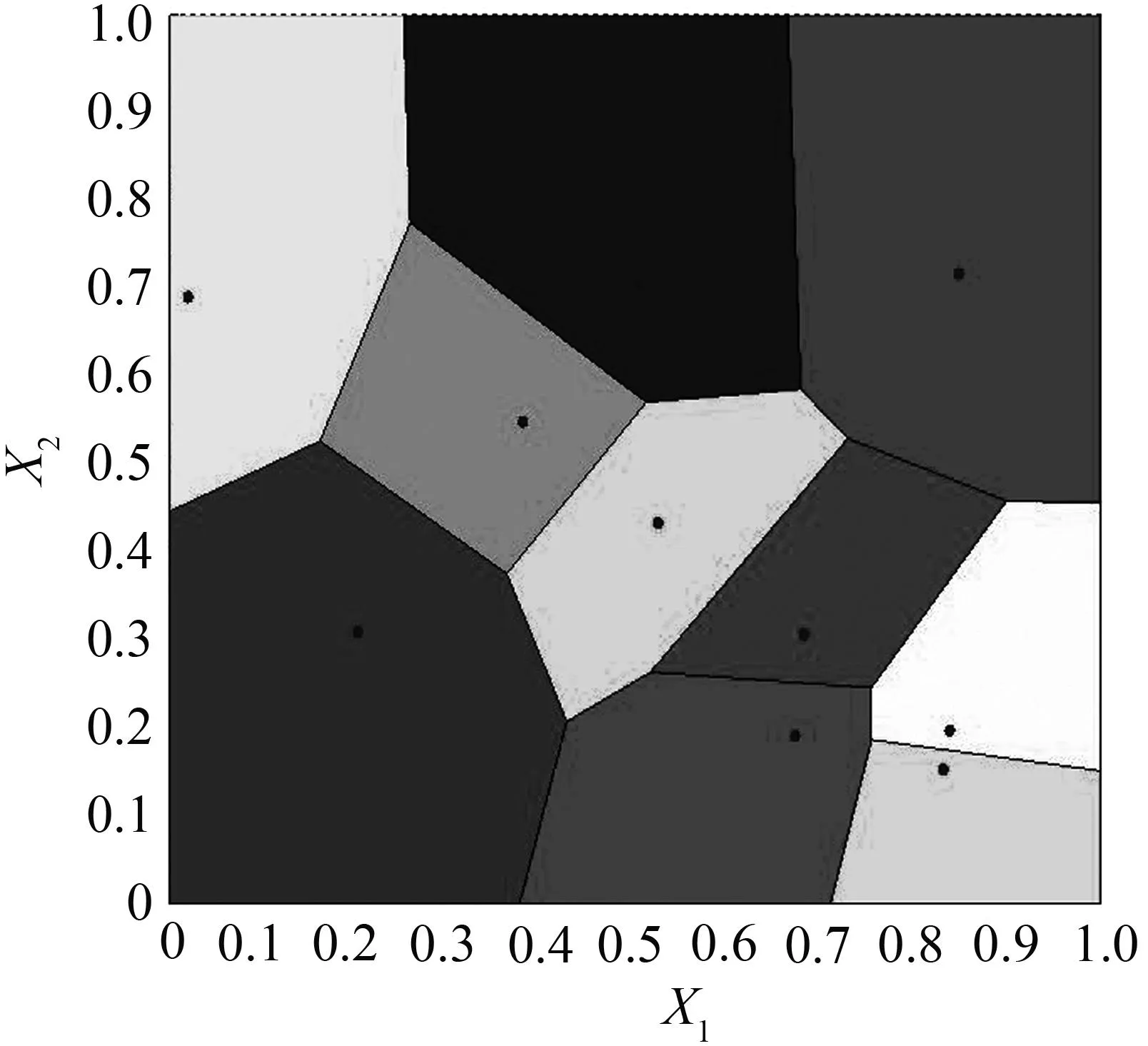
图4MATLAB中生成的二维Voronoi多晶体示意图

Fig.4Two dimensional Voronoi polycrystalline

model generated in MATLAB

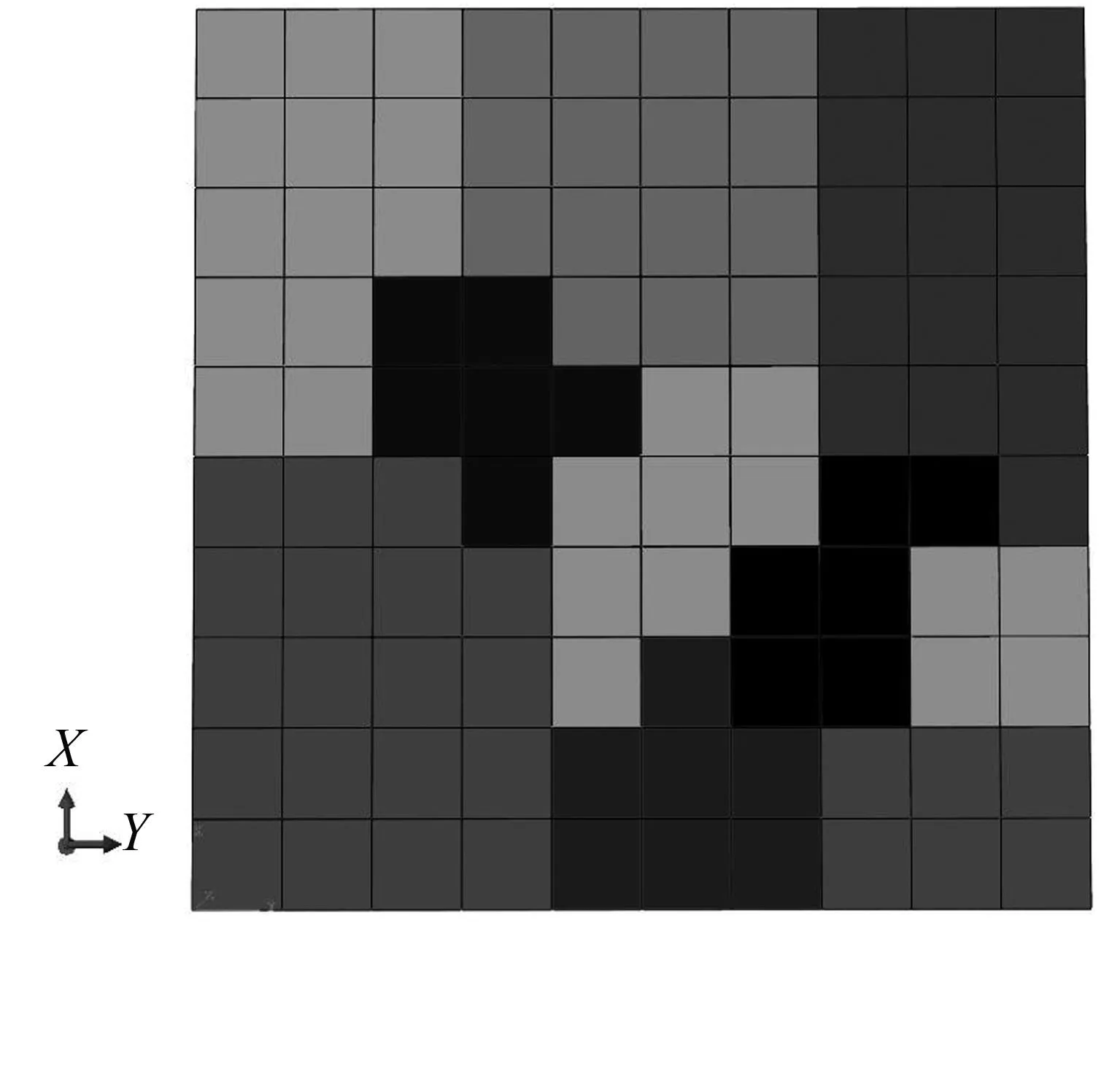
图5ABAQUS中生成的二维Voronoi多晶体模型

Fig.5Two dimensional Voronoi multi crystal

model generated in ABAQUS

2.2建立三维多晶体有限元模型

根据图3所示的三维Voronoi多晶模型建立的流程图，本文首先在MATLAB中随机生成三维空间任意分布类型的种子点，再根据随机种子点生成的三维Voronoi图。MATLAB中的三维Voronoi图如图6所示。

同样，通过MATLAB编程得到的三维Voronoi图也仅仅是带有三维Voronoi图完整拓扑信息的多晶体示意图，并不是一个带有完整边界限制的三维Voronoi多晶体有限元模型，因此本文还需要再根据图3所示流程图中的INP文件部分的分析流程进行三维Voronoi多晶体有限元模型构建。本文以建立的一个包含10个晶粒的三维多晶体有限元模型为例，其多晶体晶粒的相关参数与图6所示在MATLAB中生成的三维Voronoi图尺寸及晶粒位置、个数均相同，并通过编写ABAQUS的INP文件的形式进行实现，最终结果如图7所示。

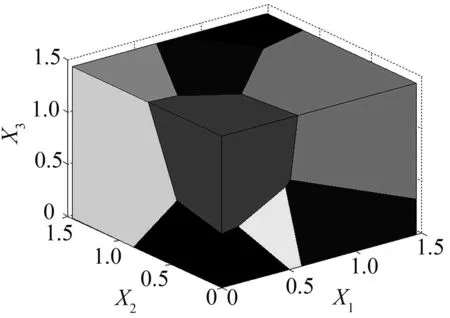
图6MATLAB中生成的三维Voronoi多晶体示意图

Fig.6The three dimensional Voronoi

generated in MATLAB

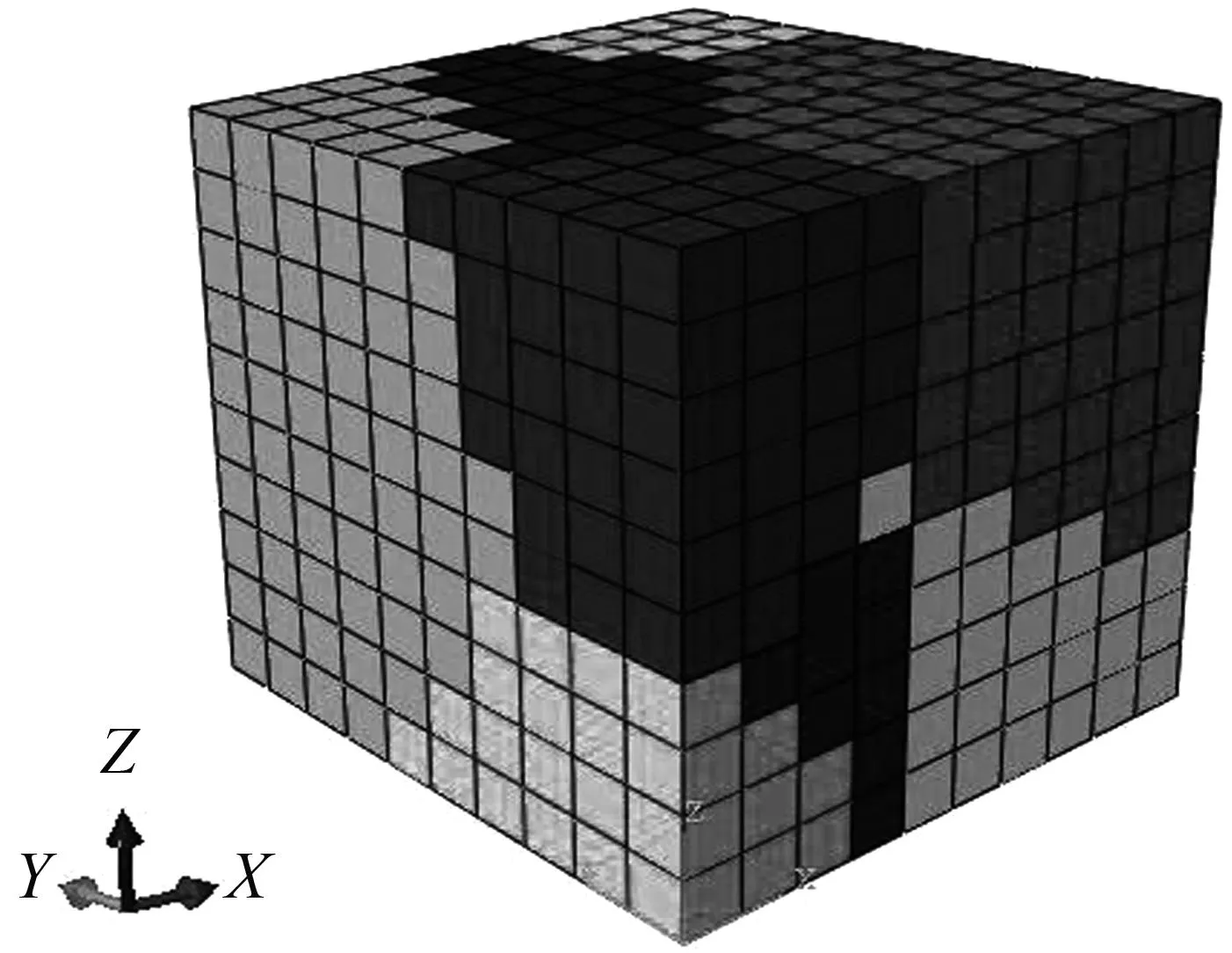
图7ABAQUS中生成的三维Voronoi多晶体模型

Fig.7Three dimensional Voronoi multi

crystal model generated in ABAQUS

3验证与讨论

为了验证本文建模方法的正确性，本文建立了与文献[9]相同晶粒数100个、相同网格类型C3D8I，相同基本尺寸1000 mm×400 mm×400 mm的Voronoi多晶有限元模型，并采用相同的本构关系、相同的约束与相同的加载方式如图8所示，还采用了相同的文献[15]中所提供的材料参数，进行了10%拉伸量的拉伸有限元模拟，结果如图9与图10所示。

图9为进行了拉伸有限元模拟之后的变形图，其表面出现了较为明显凹凸现象，这是由于晶体塑性本构关系中考虑了晶体的随机取向而导致的材料塑性变形不均匀性。

图8　ABAQUS中生成的100个晶胞的Voronoi多晶模型

图9　ABAQUS中有限元模拟后的Voronoi多晶模型变形图

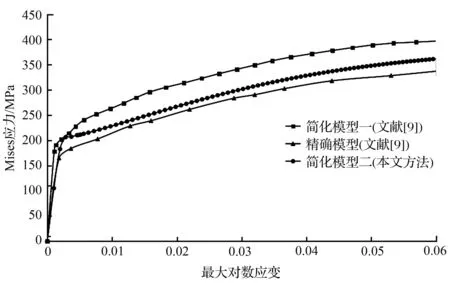
图10　相同拉伸量下不同模型单元应力—应变曲线对比

图10为不同模型单元应力—应变曲线对比图。其中简化模型一的应力—应变曲线与精确模型的应力—应变曲线均出自于文献[9]，而简化模型二的应力—应变曲线即为本文建模方法所建立的如图8所示模型，并在相同拉伸量下进行有限元模拟所得应力—应变曲线。从图10中可以看出，本文所建立的Voronoi多晶简化模型整体应力水平居于文献[9]中简化模型一与精确模型之间，在弹性区域与精确模型大部分重合但屈服点较高，并且拉伸曲线整体偏向精确模型。为了进一步深入了解本文拉伸曲线的偏向程度，本文分别在横坐标上取0.002、0.002 84、0.008、0.016、0.032、0.044、0.05与0.06等最大对数应变所对应的Mises应力值来做偏差分析。本文假设以精确模型为参考标准，以简化模型与精确模型的差值进行偏差分析来评估本文建模方法的优劣。

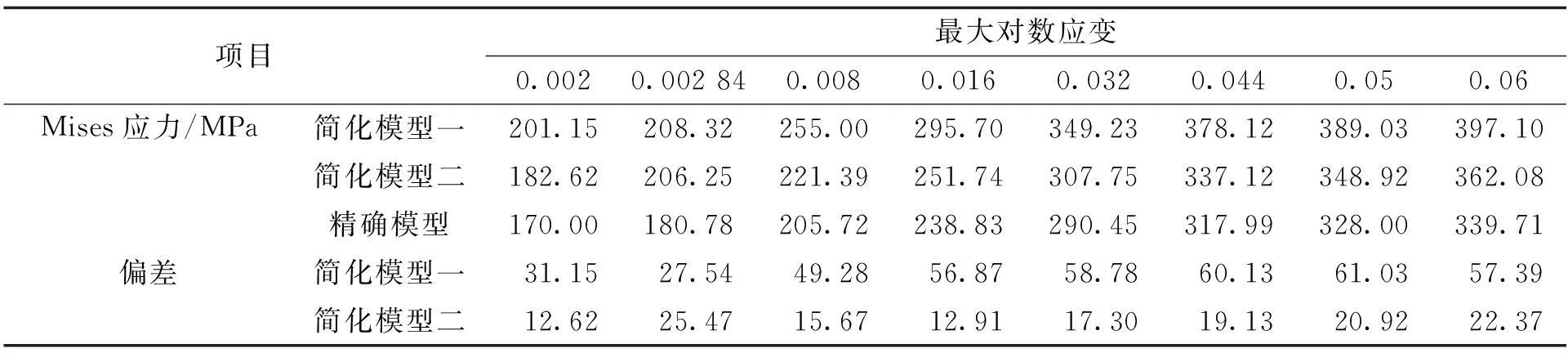
表1　相同应变下不同模型单元Mises应力数据对比

从表1中可以得到本文所建立的Voronoi多晶简化模型的应力水平与精确模型的偏差基本分布在20 MPa左右，最小偏差达为12.91 MPa，最大偏差仅为25.47 MPa，平均偏差值为18.3 MPa；而文献[9]的简化模型一与精确模型的偏差基本分布在50 MPa左右，最小偏差达到27.54 MPa(比本文所建立的简化模型最大偏差25.47 MPa还大0.07 MPa)，同时其最大偏差达到60.13 MPa，平均偏差值为50.27 MPa。因此，说明本文建立的Voronoi多晶有限元模型更接近于文献[9]的精确模型，可以用来作为金属微观结构有限元分析的模型。

4结语

①本文提出了一种基于Voronoi图并结合单元编号区域排布特点的方法，该方法可以依据单元编号区域排布特点直接得到单元编号，且更加容易实现依次求取单元形心坐标。

②二维与三维Voronoi多晶体有限元模型在判断单元归属时，均采用单元距离最近的晶核所在晶粒内的原则，可以通过改变随机数所在的区域大小，灵活地改变Voronoi多晶体有限元模型的大小。

③一旦种子点的随机坐标生成无论其顺序怎样排列，最终得到的Voronoi多晶体有限元模型均完全相同；并可以通过改变随机数的个数及分布类型，灵活地改变Voronoi多晶体有限元模型晶粒的数目及分布形态，一般晶粒数目大于50个，能够较为真实描述材料的微观组织结构。

④在相同条件下通过有限元数值分析与文献[9]的单调拉伸曲线对比，结果显示本文所建立的Voronoi多晶简化模型整体应力水平居于文献[9]中简化模型一与精确模型之间，在弹性区域与精确模型大部分重合但屈服点比较高，并且拉伸曲线整体偏向精确模型，其平均偏差值仅为18.3 MPa，而文献[9]中简化模型一的平均偏差值却高达50.27 MPa，甚至连其最小偏差也比本文所建立的简化模型最大偏差还要高0.07 MPa。从而说明本文所提出的建模方法有较高的精度与可靠度。

参考文献：

[1]赵昊,丁淑兰.ABAQUS二次开发在金属微观组织模拟中的应用[J]. 热加工工艺,2014,43(24):87-90，97.

[2]王克廷,陈忠家,郭煜泽,等.温度对合金塑性变形行为影响的蒙特卡罗模拟[J]. 有色金属加工, 2014,43(1):9-11，40.

[3]陈飞,崔振山,董定乾.微观组织演变元胞自动机模拟研究进展[J]. 机械工程学报,2015,51(4):30-39.

[4]闻瑶,薛克敏,李萍,等.TA15钛合金高温变形多晶体塑性有限元模拟[J]. 塑性工程学报, 2014,21(6):86-90，101.

[5]万朔,何力军,张伟,等.多晶铍微观弹性失配行为的数值分析[J]. 稀有金属, 2015,39(8):764-768.

[6]司良英, 邓关宇 ,吕程,等.基于Voronoi图的晶体塑性有限元多晶几何建模[J]. 材料与冶金学报, 2009,8(3):193-197，216.

[7]樊黎霞, 赵轲, 董雪花.身管径向精密锻造的塑性应变分析与锻造比研究[J]. 精密成形工程, 2014, 1(1):1-8.

[8]张丰果, 董湘怀, 章海明,等.微镦粗过程晶体塑性模型研究[J]. 塑性工程学报, 2011, 3(3):5-8.

[9]汪凯.多晶体材料加工的细观塑性有限元模拟[D]. 昆明：昆明理工大学, 2013.

[10]伊兴华.面心立方多晶体塑性变形有限元模拟[D]. 哈尔滨：哈尔滨工业大学, 2007.

[11]谢韶，唐斌，韩逢博，等.材料微结构三维建模及其晶体塑性有限元模拟[J]. 塑性工程学报， 2014,21(1):65-70.

[12]QUEY R, DAWSON P R, BARBE F.Large-scale 3D random polycrystals for the finite element method: Generation, meshing andremeshing[J]. Computer Methods in Applied Mechanics & Engineering, 2011, 200(17-20):1729-1745.

[13]FRITZEN F, BÖHLKE T, SCHNACK E.Periodic three-dimensional mesh generation for crystalline aggregates based on Voronoi Tessellations[J]. Computational Mechanics, 2009, 43(5):701-713.

[14]胡桂娟,张克实,莫智莉.45号钢后继屈服与塑性流动试验的Chaboche模型分析[J]. 广西大学学报(自然科学版),2014,39(1):171-179.

[15]HUANG Y G.A user-material subroutine incorporating single crystal plasticity in the ABAQUS finite element program[D]. Cambridge :Harvard University,1991.

(责任编辑梁健)

A method of polycrystal finite element modeling based on Voronoi diagram

ZHENG Zhan-guang1,2, WANG Zhao-liang1, FENG Qiang1, YUAN Shuai1, WANG Jia-xiang1

(1.College of Mechanical Engineering ,Guangxi University, Nanning 530004,China；2. Guangxi Key Laboratory of Manufacturing System & Advanced Manufacturing Technology,Nanning 530004,China)

Abstract:The mesoscopic polycrystal finite element (PFE) model is the premise and foundation to study the local plastic deformation of polycrystalline materials. In order to construct a reliable microstructure model of materials flexibly, a modeling method had been proposed on the basis of Voronoi diagram and regional distribution charact-eristics of units. The areal coordinates of the units could be calculated in sequence directly through the units’ num-bers by the method. Firstly, the random points and the Voronoi information in a specific plane or domain were generated. Then, the coordinates of the centers were directly calculated according to the distribution characteristics of the units’ numbers. Secondly, the nearest element was attributed to the nearest grain, the grains’ numbers and the units’ numbers were added to the part of the ABAQUS INP file by sets. Then, the PFE model was built. Lastly, taking 2D and 3D PFE models of 10 grains as examples, the stress analyses of the PFE models were compared with the results of the literature to verify the modeling method. The results reveal that the modeling method can not only directly get the units numbers and the areal coordinates of the units, but also reduces the data quantity on processing the areal coordinates of the units and the difficulties in determining the ownership of units. With the comparison, it is found that the accuracy of the model is closer to the exact model in the literature. The maximum deviation is only 25.47 MPa between the proposed model and the exact model, and the minimum deviation of the proposed model is lower than the simplified model in the literature by 0.07 MPa. It is indicated that the method can provide some references for building the Voronoi finite element model of polycrystalline materials quickly.

Key words:vonronoi diagram; polycrystal modeling; crystal plasticity; finite element method

中图分类号：TP391.41

文献标识码：A

文章编号：1001-7445(2016)02-0460-10

doi:10.13624/j.cnki.issn.1001-7445.2016.0460

通讯作者：郑战光(1975—), 男,江西临川人，广西大学副教授,博士；E-mail：zhenglight@126.com。

基金项目：国家自然科学基金资助项目(5146002)；广西自然科学基金项目(2012GXNSFBA053145)；广西制造系统与先进制造技术重点实验室项目(14-045-15S04)；玉林市科技攻关项目(玉市科攻1421001)

收稿日期：2015-11-05；

修订日期：2015-12-17

引文格式：郑战光，汪兆亮，冯强,等.一种基于Voronoi图的多晶体有限元建模方法[J].广西大学学报(自然科学版)，2016，41(2)：460-469.