特种车通过曲线部分斜拉桥的运营安全分析*

王凌波，蒋逢炜，2，招国忠，贺拴海(．长安大学公路学院，陕西西安70064; 2．中交路技术有限公司，北京00000; ．广州大广高速公路有限公司，广东广州50000)



特种车通过曲线部分斜拉桥的运营安全分析*

王凌波1，蒋逢炜1，2，招国忠3，贺拴海1
(1．长安大学公路学院，陕西西安710064; 2．中交路技术有限公司，北京100000; 3．广州大广高速公路有限公司，广东广州510000)

摘要:为研究曲线部分斜拉桥结构在超载运营时的安全状态，以某双幅部分斜拉桥为背景，采用基于空间结构有限元数值分析并考虑了计入配筋率的钢筋混凝土本构关系的方法，针对挂车－120车辆荷载，分别建立了单辆车、2辆车和3辆车以不同间距的单侧过桥模式，分析了桥梁结构首次出现开裂、截面首次进入塑性状态、单辆车通过时形成塑性铰直至结构形成机构而进入破坏阶段的全过程结构安全系数、索力分布及结构位移状况等主要力学参数，给出了结构受力特征及多辆车过桥时结构的安全系数与车辆间距的关系。研究表明，此桥在单侧通过1至3辆重120 t的挂车荷载时，其保证混凝土不开裂的最小安全系数在2. 3以上，车辆沿内幅桥通过时安全系数较高;结构安全系数与车辆间距大致呈线性关系。曲线部分斜拉桥的破坏模式为加劲梁中跨跨中截面出现塑性铰并不断扩大、主墩底截面相继出现塑性铰而形成机构，最终丧失承载能力。当多辆特种车通过曲线部分斜拉桥时，部分斜拉索的索力可能会达到设计峰值，在运营管理中应给予重视。

关键词:桥梁工程;曲线部分斜拉桥;特种车;安全系数;塑性铰

0　引言

桥梁在正常运营阶段，各部件基本处于弹性工作阶段，但随着交通量的增大，超载情况的发生，会导致结构局部应力超过材料弹性极限，使得结构局部破坏甚至结构整体垮塌［1］，研究和把握结构的极限承载能力及相应的安全系数，找到结构在破坏时刻所能承受的最大荷载和破坏模式，对掌握桥梁的安全储备、有针对性地进行管养和维护非常必要。

斜拉桥承载能力一直是工程界关注的主要研究方向之一。1985年，Nakai，Nishinuratja，Kitada［2］等以U．L．增量列式法平衡方程将钢斜拉桥主梁和主塔离散为闭合箱型截面，考虑了塔的材料非线性，进行施工和运营阶段的结构极限承载力分析，是早期比较完整的有关斜拉桥极限承载力的分析文献。此后，S Pse［3］等对预应力混凝土斜拉桥在考虑材料和几何非线性情况下对面内和面外的破坏荷载进行了研究，指出了考虑非线性的重要性;伏魁先［4］利用几何非线性原理对一座公路钢斜拉桥进行了稳定性分析，分析中用Ernst［5］公式考虑索的垂度效应;杨勇［6］分析了单索面预应力混凝土斜拉桥在中载、偏载等不同工况下的极限承载力;贺拴海［7］利用只考虑主梁的材料非线性的能量法分析斜拉桥的极限承载力。梁硕［8］结合工程实例对大跨度混凝土斜拉桥的局部与整体相关屈曲极限承载力进行分析，刘刚［9］对空间扭背索组合梁斜拉桥的几何非线性影响和结构稳定性进行了研究并与规范中稳定系数的下限值进行了对比，Gong［10］则对承受集中荷载的混凝土板桥的极限承载力进行了研究。上述分析方法基本代表了目前斜拉桥承载力分析的主要手段，分析发现，大多研究不能同时考虑材料及几何非线性，针对整体结构承载力分析及考虑钢筋影响的混凝土斜拉桥全桥承载力及安全分析研究文献较少。

20世纪80年代以来，国内外学者对部分斜拉桥开展了大量的研究。然而对曲线部分斜拉桥的研究，近5 a才渐渐展开。董水英等［11］对双塔双索面曲线部分斜拉桥的边中跨比与主梁适宜刚度进行了研究;刘昊苏等［12］研究了不同设计参数下曲线部分斜拉桥的地震响应;杨飞等［13］对双塔双索面曲线部分斜拉桥的静、动力特性进行了研究;刘凯［14］引入曲线部分斜拉桥的分类标准，对索面形式、无索区长度、布索区域位置对结构刚度的影响进行了研究;高波等［15］对双塔四索面曲线部分斜拉桥的空间稳定性进行了研究;梁田［16］研究了曲线部分斜拉桥的剪力滞效应问题;陈玉刚等［17］提出了双塔四索面曲线部分斜拉桥的主墩及索塔设计建议。部分斜拉桥的研究目前停留在设计层面上，对该桥型结构承载力分析及运营管理的研究还鲜有人问津。

桥梁在运营阶段，不可避免的会遇到各种车辆荷载的作用。随着汽车工业的发展，重型卡车的载重量越来越大，因此在桥梁运营过程中，是否允许这种特种车辆通过是一个十分重要的问题。文中以某部分斜拉桥为背景，基于有限元数值分析方法及考虑钢筋影响的混凝土本构关系，讨论特种车辆对桥梁安全性能的影响，研究通过特种车辆的数量及安全行驶间距，为结构运营管理及维护提供技术依据，以保证桥梁运营安全。

1　工程概况

某大跨度曲线矮塔斜拉桥双塔三跨空间四索面混凝土斜拉桥，采用墩、塔、梁固结体系，全桥总长424 m，采用中塔拉索承受内外幅桥的藕联设计，半幅桥宽20. 5 m，曲线内幅路线中心线孔跨(107. 76 +207. 538 + 107. 76) m，桥梁结构中心线位于R =1 786. 75 m圆曲线上;曲线外幅路线中心线孔跨为(108 + 208 + 108) m，桥桥梁结构中心线位于R =1 809. 25 m圆曲线上。主梁为预应力混凝土箱梁，断面形式为变高度单箱双室直腹断面，箱梁顶板宽20. 5 m，顶板横向设置3%的单向横坡。斜拉索采用扇形布置的高强度低松弛环氧喷涂钢绞线，单根斜拉索由55根75钢绞线组成，全桥共计72根。主桥总体布置如图1所示。为方便结构承载力及安全分析，认为混凝土和钢筋之间粘结良好，不会发生相对滑移。在某单元混凝土受压区达到极限压应变时就认为此单元已经破坏，该结构达到了承载极限。

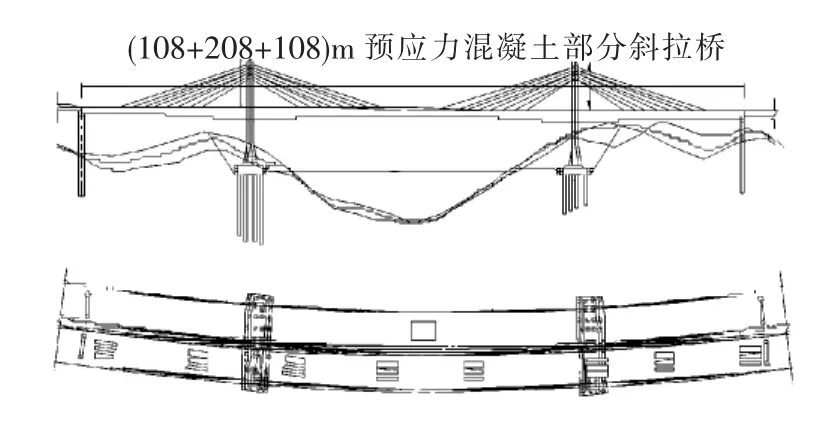
图1　主桥总体布置Fig．1 General arrangement of extradosed bridge

2　本构关系及分析方法

2. 1本构关系

对于本桥的塔及加劲梁等配筋混凝土结构，由于钢筋布置复杂，分析时使用了整体本构关系对实际构件进行描述［18－19］。即开裂前混凝土和钢筋共同受力，构件受拉开裂后由钢筋承担拉应力，即应力应变关系为

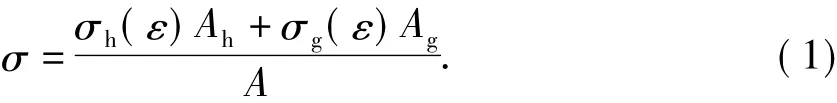
式中A为截面面积;σh为混凝土应力;σg为钢筋应力; Ah为混凝土面积; Ag为钢筋面积。

将C60混凝土截面的相关参数带入式(1)，即可得到本桥钢筋混凝土构件的钢筋混凝土结构共同工作，结构处于弹性范围;钢筋混凝土共同受力，钢筋屈服但未破坏;混凝土受拉，开裂退出工作，钢筋并未屈服;及钢筋受拉，混凝土开裂退出工作，钢筋屈服各阶段的本构关系，如图2所示。

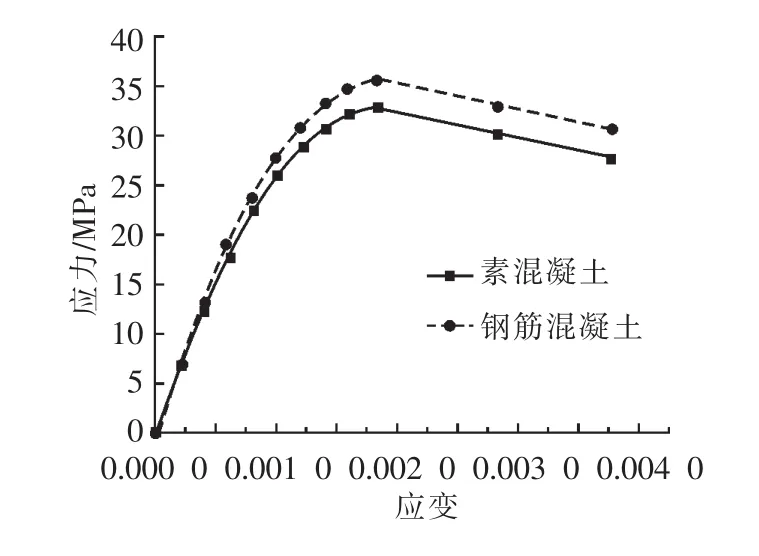
图2　素混凝土与钢筋混凝土本构关系Fig．2　Constitutive relation between plain concrete and reinforced concrete

2. 2分析方法

对于桥梁结构而言，结构内力一般由施工过程的恒载内力及运营荷载内力组成，则恒载稳定安全系数λd［20］为

式中［K1］σ为一期恒载几何刚度矩阵。荷载稳定安全系数可由式3得出

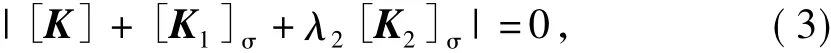
式中［K2］σ为荷载几何刚度矩阵。

如结构发生失稳前，部分构件已经进入塑性或参考荷载的刚度矩阵［K］σ与临界荷载的刚度矩阵并不存在线性关系λ［K］σ时，即为非线性稳定问题。这时，可给定的参考荷载{ F}，用考虑几何和材料非线性的有限元分析方法，将荷载逐级施加到λi{ F}，求出结构的几何刚度矩阵［Ki］σ．基于变形后的构形，由参考荷载按线性化稳定问题，即

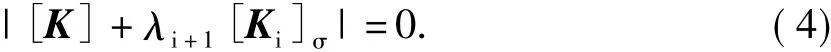
求出后期荷载安全系数λi +1．检验结构在后期屈曲荷载作用下是否出现新的弹塑性单元，如果出现则作迭代重新计算新的λi +1．则近似精确的临界荷载为

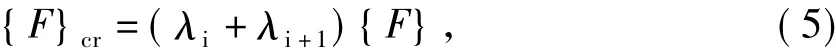
荷载安全系数为

为求得某不断增大的荷载p作用下，桥梁结构的安全系数及对应的极限承载能力，文中在确定了成桥状态的内力与构形后，按以下步骤进行简化计算:首先以成桥状态为初态，确定特种车辆的加载模式，以逐渐增加的运营荷载p进行结构的非线性分析，迭代计算至混凝土开裂、界面进入塑性、形成第一个塑性铰和实际的荷载增量倍数，检验结构是否成为机构。若是，给出极限荷载，计算结束;否则，继续增加荷载，迭代形成的塑性铰直至结构成为机构，这时荷载增量倍数即安全系数为λ，结构极限荷载为λp．

文中选用ansys进行建模计算。模型中，混凝土梁和主塔采用beam单元，斜拉索和预应力钢筋采用link单元。利用Ernst公式来修正索垂度对刚度的影响。Ansys结构离散图如图3所示。

图3　Ansys结构离散图Fig．3　Discretization analysis

3　特种车辆荷载作用下的结构安全分析

挂车－120的平板挂车如图4所示，文中以其为标准荷载进行分析。分析时，允许挂车单向通过，另一方向车辆按运营荷载方式加载。

取1～3辆特种车辆，对称于内幅桥中跨跨中布设，外幅桥布设运营荷载。多辆特种车辆间距取为0～30 m，表1给出了有限元非线性分析得出的主梁最大竖向位移、主塔横桥向位移和主塔纵桥向位移结果。图5至图7分别给出了单辆车至3辆车过桥时，主梁截面开始进入塑性时的斜拉索索力分布。

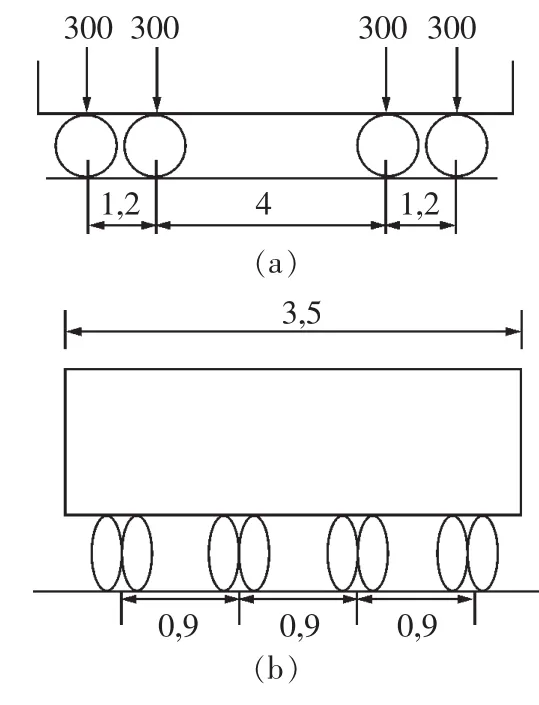
图4　特种车辆荷载Fig．4 Vehicle load(a)立面　(b)横向

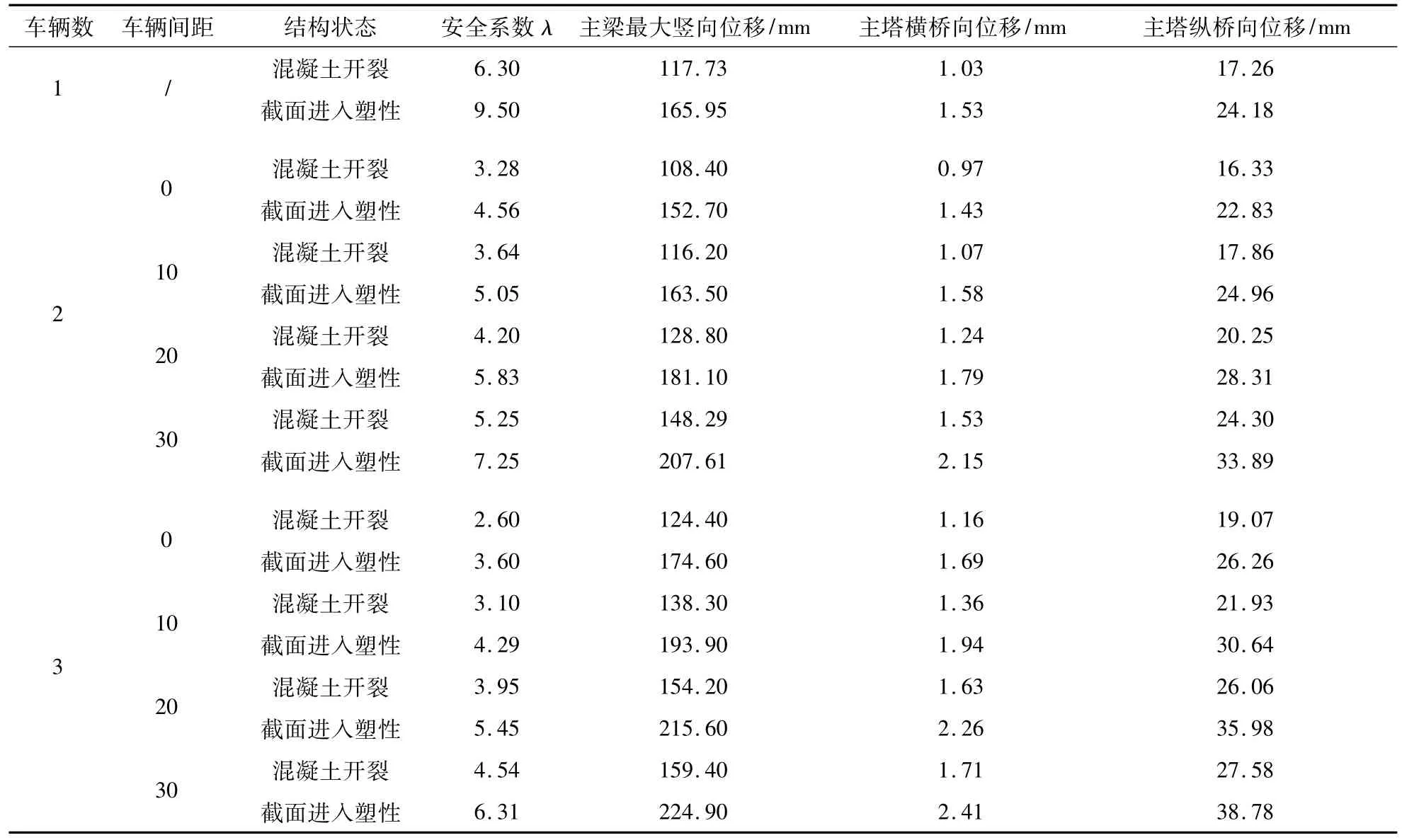
表1　特种车辆荷载作用下的结构状态、安全系数及位移Tab．1 Structural conditons，safety factors and displacement under the condition of special vehicles

可见，无论是单辆车过桥，还是多辆车过桥，其混凝土开裂的最小安全系数为2. 6，多辆车间距越大，桥梁安全越有保证。索力基本在610～750 MPa之间，同一载荷情况下索力差不超过10%．该曲线部分斜拉桥在通过3辆以内的特种车时不会引起安全事故。

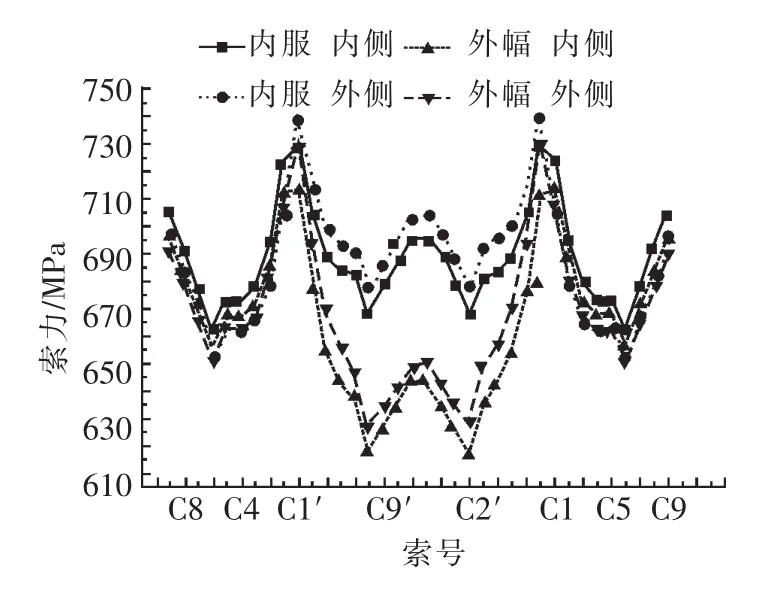
图5　单辆车作用下结构开始进入塑性时的索力分布Fig．5　Cable force distribution when single car change structure into Plastic

利用塑性铰原理，单辆特种车为基准，进一步分析该斜拉桥的极限承载力。则当荷载系数增加到9. 5时，曲线内侧桥梁中跨跨中截面出现第一个塑性铰，并随着荷载的增加，该塑性铰的塑性区域不断扩大，当荷载系数增大到16. 1时，墩底截面出现第二个塑性铰，跨中截面塑性区域扩展到悬臂浇筑段，结构主梁挠度达到1. 56 m，结构此时成为机构而破坏。此时对的结构位移荷载曲线及破坏时刻索力如图8所示。

进一步分析2辆及3辆车作用时的结构破坏模式表明，结构均以加劲梁中跨跨中截面出现塑性铰并不断扩大、主墩底截面相继出现塑性铰的形式而形成机构，使得桥梁结构丧失了承载能力。

将通过2辆及3辆特种车辆时桥梁跨中截面出现开裂及钢筋屈服2种时刻的车辆间距－结构安全系数曲线绘于图9中。

分析图9并结合表1可知，内幅桥在多辆特种车作用下，随着车辆间距的增大，可以承受的最大荷载也不断增大，间距与荷载安全系数大致呈线性关系;随着特种车数量的增加、车辆间距的减少，主梁位移不断增大;在桥梁运营阶段，可以根据图9大致确定不同间距下保证桥梁不发生混凝土开裂的安全系数。为了保证桥梁运营阶段主梁不出现混凝土开裂，应尽量增大车辆的间距，增加桥梁所能承受荷载的富余度。

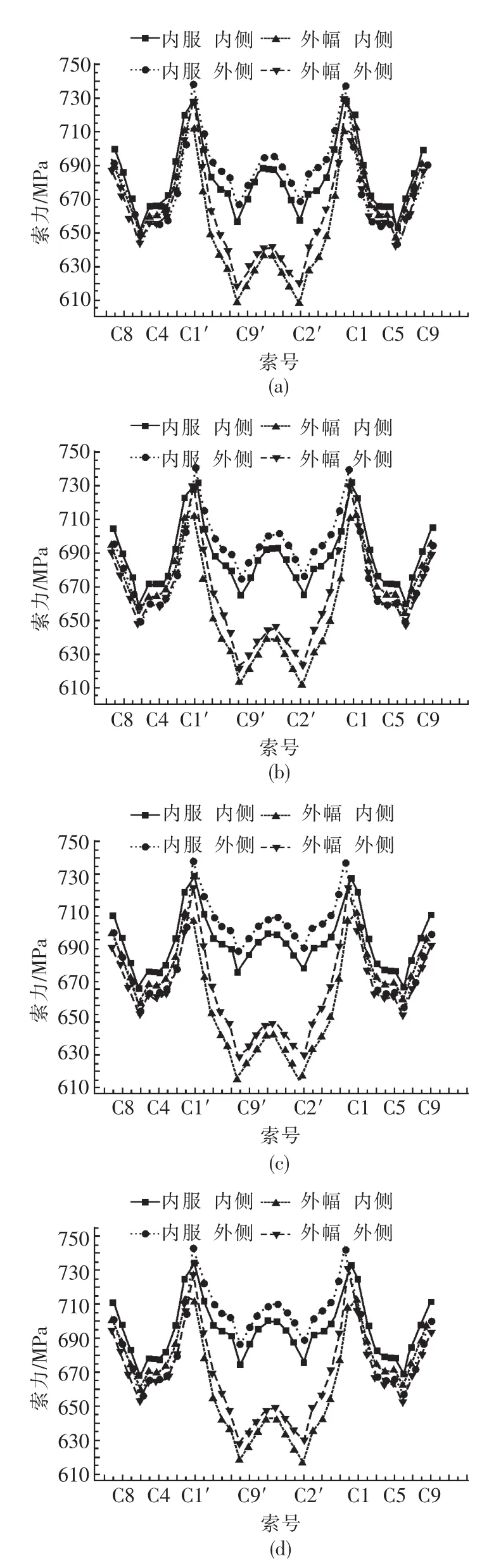
图6　2辆车作用下结构开始进入塑性时的索力分布Fig．6　Cable force distribution when double cars change structure into plastic

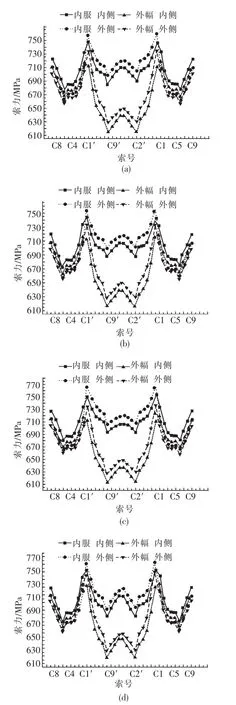
图7　3辆车作用下结构开始进入塑性时的索力分布Fig．7　Cable force distribution when triple cars change structure into plastic

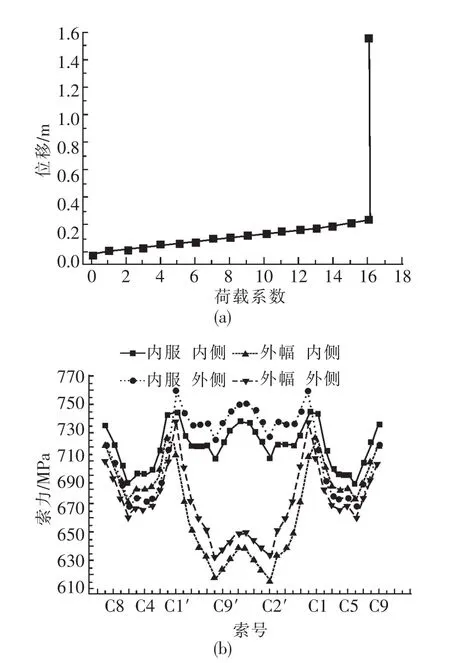
图8　单辆车工况结构破坏时的力学特性Fig．8　Mechanical properties of structure damage with single car

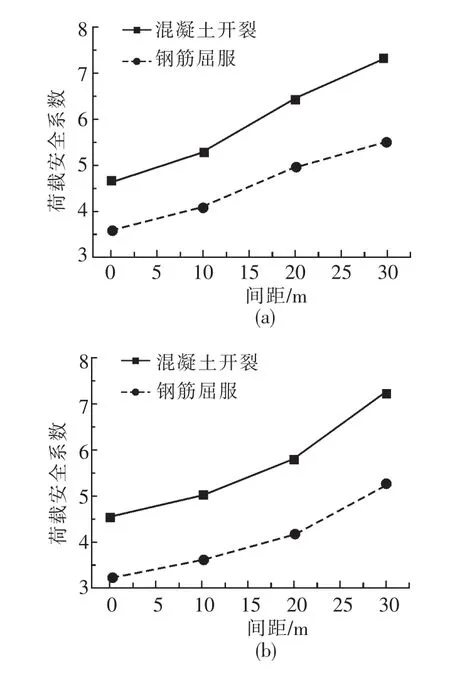
图9　车辆间距与荷载安全系数曲线Fig．9 Safety factor curve between vehicle spacing and load

若将特种车按同样的方式布置在外幅桥上，而内幅桥布设运营荷载，分析结果表明:结构的受力特点与特种车布置在内幅桥上类似，但荷载安全系数略小，1～3辆车，分别布设于内、外幅桥上的荷载最小安全系数分别为6.3，6.08，3.28，2.91，2.6，2.3.

4　结论

1)部分斜拉桥在单辆车及多辆车荷载作用下，结构的破坏模式均为为加劲梁中跨跨中出现塑性铰并不断扩大、主墩底截面相继出现塑性铰而形成机动，使得桥梁结构失去承载能力。对曲线部分斜拉桥而言，单辆车作用时，斜拉索的安全富余度较高;多辆特种车过桥时内幅外侧的斜拉索索力较大，距离主塔0. 2 L处的斜拉索索力会达到峰值，应给予重视;

2)曲线内、外幅当通过一辆挂车－120特种车辆时，安全系数较高;当需要通过多辆时，需要按照一定的车辆间距进行通行;

3)多辆特种车辆的过桥间距与结构安全系数的关系密切，随着车辆间距的增大，结构的安全系数相应增大，且呈近似线性关系;

4)单辆特种车为基准，并逐步增大荷载系数可得到曲线部分斜拉桥的极限承载力。当荷载系数增大到16. 1时，桥墩墩底截面会出现第二个塑性铰，主梁跨中截面塑性区域扩展到悬臂浇筑段，结构此时成为机构而破坏。

参考文献References

［1］韩江水，张玲，袁涌．斜拉桥抗震性能评价［J］．西安科技大学学报，2013，33(2) : 131－135. HAN Jiang-shui，ZHANG Ling，YUAN Yong．Evaluation of seismic resistance capacity for cable-stayed bridge［J］．Journal of Xi’an University of Science and Technology，2013，33(2) : 131－135.

［2］田中克弘，北田俊行．弾塑性有限変位解析によるニールセン·ローゼ橋および斜張橋の耐荷力照査法について［C］/ /鋼構造論文集．东京:日本钢构造协会，2001: 39－49．TANAKA Katsuhiro，Tbshiyuki KITADA．Checking method for load carrying capacity of nielsen-lohse bridges and cable-stayed bridges through elasto-plastic and finite displacement analysis［C］/ /JSSC: Journal of Steel Structures＆Construction．Tokyo: Steel Structure Association of Japan，2001: 39－49．

［3］Seif S P，Dilger W H．Nonlinear analysis and collapse load of P/C cable-stayed bridges［J］．Journal of Structural Engineering，2014，116(3) : 829－849.

［4］伏魁先，刘学信．斜拉桥面内整体失稳分析［J］．铁道学报，1993，15(4) : 74－79. FU Kui-xian，LIU Xue-xin．An analysis of cable-stayed bridges on global in-plane instability［J］．Journal of Railway Society，1993，15(4) : 74－79.

［5］Ernst J H，Der E．Modul von seilen unter beruecksichtigung des durchhanges［J］．Der Baningenieur，1965，40 (2) : 52－55.

［6］杨勇．PC单索面斜拉桥极限承载力分析［D］．上海:同济大学，1994. YANG Yong．Ultimate bearing capacity analysis of PC cable-stayed bridges with single plane［D］．Shanghai: Tongji University，1994.

［7］贺拴海，刘志文，宋一凡．斜拉桥的极限承载力分析［J］．中国公路学报，2000，13(3) : 53－57. HE Shuan-hai，LIU Zhi-wen，SONG Yi-fan．Analysis for ultimate load capacity of cable-stayed bridges［J］．China Journal of Highway and Transportation，2000，13(3) : 53 －57.

［8］梁硕．肋板结构主梁混凝土斜拉桥相关屈曲极限承载力空间分析［J］．土木工程学报，2001，34(5) : 45 －51. LIANG Shuo．Three dimensional analysis for local overall interative bucking load［J］．China Civil Engineering Jounal，2001，34(5) : 45－51

［9］刘刚．空间扭背索组合梁斜拉桥极限承载力分析［D］．西安:长安大学，2010. LIU Gang．Analysis for ultimate bearing capacity of space-twisting cable hybrid girder cable-stayed bridge ［D］．Xi’an: Chang’an University，2010.

［10］GONG Jin-xin，ZHANG Yan-qing，HAN Shi．Ultimate bearing capacity of reinforced concrete slab carrying concentrated load［J］．Journal of Engineering Mechanics，2011，137(12) : 877－886．

［11］贺拴海．桥梁结构理论与计算方法［M］．北京:人民交通出版社，2003. HE Shuan-hai．Bridge structural theory and calculation method［M］．Beijing: China Communication Press，2003.

［12］董水英，杨飞，杨昀．曲线部分斜拉桥边中跨比及主梁适宜刚度研究［J］．公路交通科技，2012(10) : 71－77.DONG Shui-ying，YANG Fei，YANG Yun．Research of ratio of side span to central span and suitable stiffness of main beam of curved extradosed cable-stayed bridge ［J］．Journal of Highway and Transportation Research and Development，2012(10) : 71－77.

［13］刘昊苏，董军，杨昀．不同设计参数下曲线矮塔斜拉桥地震响应分析［C］/ /第21届全国结构工程学术会议论文集第Ⅱ册，2012: 258－260. LIU Hao-su，DONG Jun，YANG Yun．Seismic analysis of curve extradosde cable-stayed bridge based on different design parameters［C］/ /21th National Conference on Structure Engineering，2012: 258－260.

［14］杨飞，杨昀，王晓雷，等．曲线部分斜拉桥静、动力特性研究［J］．公路交通科技:应用技术版，2012 (10) : 166－171. YANG Fei，YANG Yun，Wang Xiao-lei，et al．Static and dynamic analysis of curved extradosed cable-stayed bridge［J］．Journal of Highway and Transportation Research and Development: Application Version，2012 (10) : 166－171.

［15］刘凯．曲线部分斜拉桥的几个设计参数研究［D］．西安:长安大学，2013. LIU Kai．Study on several design parameters of curve extradosde cable-stayed bridge［D］．Xi’an: Chang’an U-niversity，2013.

［16］高波，邓成刚，王立新，等．曲线部分斜拉桥空间稳定性能研究［J］．公路，2014(7) : 14－21. GAO Bo，DENG Cheng-gang，WANG Li-xin，et al．Space stability study on curve extradosde cable-stayed bridge ［J］．Highway，2014(7) : 14－21.

［17］梁田．曲线矮塔斜拉桥剪力滞效应研究［D］．北京:北京建筑大学，2014. LIANG Tian．Study on shear lag effect of curve extradosde cable-stayed bridge［D］．Beijing: Beijing University of Civil Engineering and Architecture，2014.

［18］肖荦彪，肖伟．多塔斜拉桥温度场边界条件数值模拟［J］．成都师范学院学报，2013，29(7) : 118－121. XIAO Luo-biao，XIAO Wei．Numberical simulation on boundary conditions of temperature field in multi-pylons cable stayed bridges［J］．Journal of Sichuan College of Education，2013，29(7) : 118－121.

［19］李宏江，王荣霞，王磊．在役预应力混凝土斜拉桥的结构状态模拟［J］．中外公路，2013，(1) : 154－158. LI Hong-jiang，WANG Rong-xia，WANG Lei．Simulation on structural state of PC cable-stayed bridges in service ［J］．Journal of China＆Foreign Highway，2013，(1) : 154－158.

［20］陈玉刚，赵启华，樊启武．黄龙带曲线矮塔斜拉桥主墩及索塔设计［J］．四川建筑，2015，35(1) : 132－134. CHEN Yu-gang，ZHAO Qi-hua，FAN Qi-wu．Main pier and cable tower design of curve extradosde cable-stayed bridge［J］．Sichuan Architecture，2015，35(1) : 132－134.

Operational safety analysis of special vehicle driving through an extradosed bridge with curve shape

WANG Ling-bo1，JIANG Feng-wei1，2，ZHAO Guo-zhong3，HE Shuan-hai1
(1．Highway School，Chang’an University，Xi’an 710064，China; 2．Road and Bridge Consultants Co．，Ltd．，Beijing 100000，China; 3．Guangzhou Daguang Highway Co．，Ltd．，Guangzhou 510000，China)

Abstract:In order to study the structural safety status in overload conditions of curve extradosed bridge，a double-amplitude extradosed bridge is analyzed based on FEA numerical methods，considering the effects of reinforced concrete constitutive relation，three unilateral bridge models are designed for single veihicle，double veihicles and triple veihicles with different spacing in Trailer－120 vehicle load．Main mechanical parameters are analyzed，such as first crack appears on bridge structure，cross section first goes into plastic，the safety factor for whole process from plastic hinge formed to the structure forming mechanism and finally stepped into damage stage when single vehicle passing by，cable force distribution and structural displacement．The structure features and the relationship between safety coefficient andbook=289,ebook=142vehicle spacing when more veihicles go through the bridge are put forward．The research shows that: firstly，when no more than three veihicles with 120 ton weight go through unilateral bridge，the minimum safety factor of concrete cracks is above 2. 3，and safety factor incrases when veihicles passing along the inside of the bridge．Secondly，structure safety factor and vehicle spacing has linear relationship．Finally，structure destruction all happened when plastic hinge appeared and expanded in the midspan and main pier bottom sections in the stiffening beam，then lose the whole bridge bearing capacity．When three special cars go through the curve extradosed bridge，a part of cable force may reach the design peak，which should be given attention in operation management．

Key words:bridge engineering; extradosed bridge with curve shape; special vehicle; safety factor; plastic hinge

通讯作者:王凌波(1984－)，女，陕西西安人，工学博士(博士后)，副教授，E-mail: Dr．wlb@ qq．com

基金项目:中国博士后基金项目(2015M572511) ;广东省交通运输厅科技项目(科技－2014－02－017) ;中央高校基本科研业务费资助项目(310821153306)

*收稿日期:2015－10－22责任编辑:李克永

DOI:10．13800/j．cnki．xakjdxxb．2016．0222

文章编号:1672－9315(2016) 02－0288－08

中图分类号:U 441

文献标志码:A