计及短路电流限制的输电网双层扩展规划模型
宋柄兵 顾 洁
(1.上海交通大学电力传输与功率变换控制教育部重点实验室 上海 200240
2.上海交通大学电子信息与电气工程学院 上海 200240)
计及短路电流限制的输电网双层扩展规划模型
宋柄兵1,2顾洁1,2
(1.上海交通大学电力传输与功率变换控制教育部重点实验室上海200240
2.上海交通大学电子信息与电气工程学院上海200240)
摘要在传统输电网规划中考虑限流措施的优化配置,建立计及短路电流限制的输电网双层扩展规划模型。上层规划模型以输电线路投资和限流电抗器配置投资总成本最小为目标,下层规划模型在上层规划模型得出的线路方案下以限流电抗器优化配置投资最小为目标,上下层交互影响作用,最终由上层规划模型给出满足短路电流水平要求的总体规划方案,包括输电线路建设方案和限流电抗器配置方案。将遗传算法和粒子群算法相结合求解所建立的输电网双层扩展规划模型,并通过18节点算例及其扩展算例验证了该模型和算法的有效性。
关键词:输电网扩展规划短路电流裕度限流电抗器优化配置双层优化混合优化算法
0引言
随着电网负荷需求的不断增加,电网结构趋于复杂。电网作为居民生产、生活的动力命脉,其安全稳定性直接影响用户的供电可靠性。负荷的增长、电源容量的增加以及电网规模的扩大导致电网短路电流水平不断增大,在提高对断路器开断能力要求的同时,直接威胁到电网的安全,甚至可能会导致互联系统的解裂崩溃。
短路电流增长过快已成为影响电网,尤其是大型地区电网规划和运行的重大问题,近十年来,上海、广州、深圳等地区的电网都不同程度地面临着短路电流水平增大的困扰。随着上海地区接受区外来电容量、本地装机容量的增加和电网网络结构的不断加强,网络短路容量进一步升高。目前上海电网通过分层分区运行的方式[1],降低较低一级的电网短路电流水平。广州电网在迎峰度夏时期还采取了部分变电站母线分列运行、部分线路开环运行的方式[2],进一步降低短路电流。文献[3]表明通过对电网的优化分区,既可以解决分区短路电流超标问题,又能满足分区运行的可靠性和可扩展性。文献[4]给出了考虑装设限流电抗器、母线分列运行等多种电力系统限流措施的优化配置方案,以更经济地降低电网短路电流水平。文献[5]则将短路电流水平作为控制量添加到最优潮流模型中,更合理地分配新增的发电机容量,在保证短路电流裕度的前提下,实现电网的经济可靠运行。总体来看,国内外对短路电流水平控制的研究主要集中在电网成型后网络结构优化和限流措施的应用上,但在电网规划方案形成过程中如何优化考虑短路电流的影响还没有深入研究和应用。传统的输电网规划在网架确定之后进行短路电流校验,忽略了短路电流对电网优化规划的重要导向作用,未能从电网规划层面考虑限流措施的应用;合理平衡短路容量和输电容量,既保证电网的安全可靠,又留有一定的短路电流裕度,有助于电网的长期持续可靠发展。
本文首先阐述电网短路电流的影响因素和典型限流措施的基本电气模型,将短路电流限制措施作为控制量加入到传统的输电网规划模型中,在此基础上综合考虑扩建成本和限流措施成本,建立计及短路电流限制的输电网双层扩展规划模型;然后采用基于遗传算法和粒子群算法的混合算法求解双层优化模型,以提高计算效率;最后通过标准算例说明本文工作的有效性。
1短路电流的影响因素及典型限流措施模型
1.1影响因素
系统短路电流的大小与序网阻抗有关,电网网架确定后,根据实际运行方式可以计算系统的短路电流。网架构建的合理性关系到用户供电的可靠性,也对整个电网的短路电流水平产生影响。当电网中某一节点f发生三相对称短路故障时,如图1所示。

图1 电网故障示意图Fig.1 Fault diagram of power system
故障点f处的短路电流可简化为
(1)

当电网短路电流水平较高时,通常需要调整系统的运行方式以及采取限流措施等来抑制短路电流,确保电网的安全稳定运行。限流措施通过改变系统的阻抗矩阵(或导纳矩阵),从而提高短路点的自阻抗,以降低短路电流。
1.2基本限制措施及限流模型
常用的限流措施有电网分层分区运行、母线分列运行、加装限流电抗器和加装故障限流器[6]等。2008年,华东电网有限公司在泗泾变电站实施了首台500 kV线路串联电抗器成套装置示范工程[7],成功解决了枢纽站面临的短路电流超标问题。鉴于加装限流电抗器的实用性和其目前在我国电网应用的可能性,本文主要考虑采取该措施来降低系统短路电流,图2为加装线路电抗器等效图。
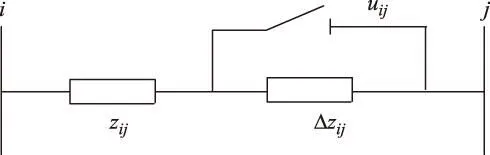
图2 加装线路电抗器等效图Fig.2 Equivalent model of installing line reactor
加装线路限流电抗器不影响原导纳矩阵阶数,只改变了母线i和j的自导纳和互导纳,改变量为
(2)
(3)
式中,uij=0表示开关闭合,即线路不加装限流电抗器,uij=1表示开关断开,即线路加装限流电抗器;Δzij为加装限流电抗器的阻抗值,Ω;zij为原输电线路阻抗值,Ω。
影响限流电抗器成本的主要因素是其容量,按照国标GB/T 1094.6—2011给出的电抗器容量公式[8],限流电抗器的成本函数可近似为
(4)
式中,cR为一组三相限流电抗器的造价成本,万元;IN为限流电抗器的额定电流,kA;ZR为限流电抗器的阻值,Ω;k为单位容量限流电抗器造价成本,万元/MV·A,参考现有的电抗器造价得出。
2计及短路电流限制的输电网双层规划
传统的输电网规划模型仅考虑线路的投资成本和运行成本,在网架形成后进行可靠性和短路电流等校验,未能在形成规划方案时综合考虑到将来可能出现的短路电流超标、短路电流裕度不足等问题及其应对办法。本文选取加装限流电抗器这一典型短路电流限制措施,将其引入输电网扩展规划模型中,在电网规划层面预留限流电抗器应用空间,降低短路电流超标问题处理成本。
考虑限流电抗器优化配置的输电网扩展规划问题的决策变量包含新建输电线路的位置和回数、限流电抗器的加装位置和容量,具有更高的维数和复杂度,给问题求解带来困难。本文基于两层规划理论,将原问题分为两层求解,由上层规划给出满足系统运行约束的输电线路规划方案,由下层规划给出满足系统短路电流约束的限流电抗器配置方案,通过反复迭代、交互上下层规划方案,最终得出最优解,有效降低了原问题求解难度。考虑限流电抗器优化配置的输电网双层扩展规划模型,能在构建优化网架的同时,通过对限流电抗器的优化配置降低短路电流,实现电网规划安全与经济综合优化。
2.1两层规划理论
两层规划按下层反应情况分为两类:①下层以最优解作为最佳反应,要求对上层规划的每一决策,下层规划决策惟一;②下层以最优值作为最佳反应,不要求下层规划决策的惟一性,其一般形式为

s.t. x∈X={x:H(x)≤0}
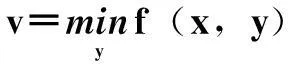
s.t. y∈Y={y:G(x,y)≤0}
(5)
式中,x为上层规划的决策变量;v为下层规划的最优值;F(x,v)为上层规划的目标函数;X为上层规划中决策变量的可行域;H(x)≤0表示上层规划中决策变量x所满足的约束条件;y为下层优化的决策变量;f(x,y)为下层规划的目标函数;Y为下层优化中决策变量的可行域;G(x,y)≤0表示上层规划给定决策x时下层规划中决策变量y满足的约束。
下层以最优值为最佳反应的两层规划的最优解(x*, y*)满足
F(x*, f(x*,y*))≤F(x, f(x,y))
(6)
式中,(x,y)为满足上下层规划约束条件的任一可行解。
2.2上层规划模型
上层规划模型以输电网扩展规划线路投资成本、限流电抗器配置成本之和F最小为目标
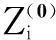
上层规划模型的约束条件有:
1)满足正常运行方式下及N-1安全性的潮流平衡约束。
(8)
(9)
(10)
(11)
∀i∈NB,∀l∈LL
式中,PGi和QGi分别为节点i的发电机有功和无功功率注入;PLi和QLi分别为节点i的有功和无功负荷;Pi(Z)和Qi(Z)分别为规划方案Z中节点i的线路有功和无功潮流流出;上标N为正常运行方式,N-1为一回线路故障时系统运行方式;l为规划方案Z在N-1运行条件下断开的线路编号;NB为所有节点集合;LL为规划方案Z所有线路集合。
2)线路扩建约束。
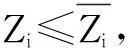
(12)
3)节点电压约束。
(13)
(14)
∀i∈NB,∀l∈LL式中,Umax和Umin分别为系统所允许的电压上下限,kV。
4)线路传输容量约束。
(15)
(16)
∀L∈LL,∀l∈LL, L≠l
式中,SL为规划方案Z中线路L实际传输容量;SL,max为线路L最大允许传输容量。
2.3下层规划模型
下层规划模型以限流电抗器优化配置成本CS最小为目标函数。
(17)
式中,CS为在线路上采用限流电抗器措施配置成本,万元;cR为在线路上采用限流电抗器限流的成本函数;u为限流措施配置的位置信息,u=[u1…uM], 表示支路1~M是否应用限流电抗器,ui=1表示支路i加装限流电抗器,ui=0表示不加装;v为限流电抗器的阻抗参数,v=[v1…vM], 表示支路1~M的限流电抗器的阻值,Ω。
为评估输电网扩展规划方案的短路电流水平,使得规划方案更灵活的适应未来系统网架及潮流分布的变化,定义系统短路电流裕度[9]指标γf为
(18)
式中
(19)
式中,γf,i为节点i的短路电流裕度,kA;Ifspec为系统所允许的最大短路电流,kA;If,i为节点i的短路电流,kA。
下层规划模型的约束条件有:
1)含限流措施的潮流平衡约束。
(20)
(21)
(22)
(23)
∀i∈NB,∀l∈LL
式中,Z*为上层规划模型求解得出的最优解。
2)节点电压约束。
(24)
(25)
∀i∈NB,∀l∈LL
3)线路传输容量约束。
(26)
(27)
∀L∈LL,∀l∈LL, L≠l
4)规划方案短路电流裕度指标约束。
γf≥γfspec
(28)
式中,γfspec为系统所允许的最小短路电流裕度;γf越大,该系统最大短路电流越小。
5)限流措施数量约束及限流措施参数约束。
ui∈{0,1}
(29)
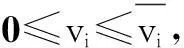
(30)
(31)
(32)
式中,NSR为系统允许投运的限流电抗器总数量;ZS为系统允许投运的电抗器总阻抗值,因为过量投运限流电抗器将增加系统网损,影响系统正常运行。式(29)表示限流措施是否采用,ui=0表示不采用,ui=1表示采用。式(30)表示限流电抗器的阻抗参数,考虑到实际情况,限流电抗器的阻值不可能是任意数值,为简便起见,本文取电抗器的阻值为整数值,实际系统中可根据具体情况选取,并不影响本文模型的应用。式(31)和式(32)分别表示系统允许投运电抗器总数量约束和系统允许投运电抗器总阻值约束。
2.4上下层规划模型之间的逻辑联系
上层规划模型以新增候选输电线路的架设为决策变量,采用新建线路成本、限流电抗器配置成本之和最小为优化目标,将线路投建方案传递给下层。下层规划模型以限流电抗器投运位置和容量为决策变量,以限流电抗器配置成本最小化为目标函数,得到限流电抗器的优化配置结果,并将该配置结果返回给上层规划模型,根据新的网络参数更新上层规划模型中的限流电抗器配置成本。上层模型再次进行优化规划,反复交替进行上述步骤,实现上下层模型之间的协调反馈,确保上下层模型都满足相关约束,最终得出输电网优化规划方案。
上下层规划模型之间的联系如图3所示。
根据初期坝现有设计相关参数进行计算,局部坝面坡度调整和斜马道宽度,满足以下条件即可具备本方法的修筑条件(考虑到车辆通行,并与现有村村通保持一致,建议b2≥4.5 m):

图3 上下层模型的逻辑联系Fig.3 General view of relationship between the upper and lower model
3基于遗传-粒子群混合算法的模型求解
计及短路电流限制的输电网双层规划模型是一个混合整数非线性规划问题,具有高维度和高复杂性特征。本文采用基于遗传算法和粒子群算法的混合算法求解该模型。利用遗传算法处理上层规划模型中的整数变量,对下层规划采用粒子群算法完成限流电抗器的优化配置,充分发挥智能优化算法的计算优势,取得较高的计算效率。
3.1遗传算法求解上层规划模型
本文采用染色体整数编码的遗传算法,对于规划方案Z中的每一参数,即每条支路的最终线路数目,根据支路已有线路数目和最大允许线路数目确定其取值的上下限,并随机生成满足线路扩建约束的个体。为保证生成个体的有效性,采用节点标记算法(Node Marking Algorithm,NMA)[10]快速校验个体网络拓扑的连通性。对于网络拓扑不连通的个体,采用染色体修补法[11],随机添加一条或多条待选线路的方法,使个体网络拓扑连通,并修正个体的对应染色体参数。本文采用轮盘赌选择法,将总投资成本作为适应度函数来评价方案的优劣。交叉操作采用两点交叉,变异操作采用多点均匀变异。在整个进化过程中,始终保留前一代最好个体,当在新种群中出现更好的个体时,以其替代原先最好个体,最终进化结束后的最好个体即为该问题的最优解。
3.2基于筛选策略的离散粒子群算法求解下层规划模型
限流电抗器的优化配置问题的解包含采用线路电抗器限流的支路编号和对应线路的限流电抗器阻抗。下层规划模型中的系统允许投运的限流电抗器总数量约束限制了采用限流电抗器限流的支路数目,因此,筛选出对系统短路电流降低最显著的NSR条支路作为限流电抗器的待选投运位置,能有效降低原问题求解的维数。本文所采用的筛选指标即限流电抗器投运的灵敏度。支路l加装线路电抗器对限制节点k短路电流效果的限流灵敏度βkl[12]为
(33)
式中,i、j为支路l两端的节点;zl0为支路l的初始阻抗;Zki和Zkj分别为节点k与i、 节点k与j的互阻抗。
对于实际电网,需考虑所选用限流措施对所有系统节点的限流效果,因此定义支路l加装线路电抗器的综合灵敏度指标为
(34)
式中,Ω为短路电流裕度小于γfspec的节点集合。
限流电抗器优化配置模型的求解算法大致如下:
根据加装限流电抗器的灵敏度β, 确定待选加装线路电抗器的支路编号,形成采用限流电抗器措施的待选支路集合,采用离散粒子群算法DPSO求解。

3.3计及短路电流限制的输电网双层规划模型求解流程
采用遗传-粒子群混合算法求解本文提出的双层规划模型的主要流程如下:
2)随机生成n个个体Z(1), Z(2), …, Z(n)。
3)对每一个候选方案Z(i)(i=1, 2, …, n)验证是否满足上层规划模型的约束条件,若满足,则利用基于筛选策略的离散粒子群算法求解下层规划模型,得出该方案对应的限流电抗器最优配置结果,并反馈给上层模型,得出上层模型的目标函数值;反之,令目标函数值为一大数。
4)对每个个体计算适应度函数值,适应度函数最小的个体即为当前最优解,保留该个体,若下一次迭代产生了更好的个体,则替代前面保留的个体。
5)若连续100次迭代得到的最优个体都相同,则结束迭代过程,并取该个体为最优规划方案,输出对应的线路规划方案和限流措施配置方案;否则,对N个个体进行选择、交叉和变异操作,形成新的群体,转步骤3。
4算例分析
测试算例采用18节点系统[14]和基于18节点系统扩展的19节点系统说明所提出的计及短路电流限制的输电网双层扩展规划模型的可行性和有效性。
4.118节点测试系统
该系统现有10个节点、9条线路,基准电压500 kV,基准容量500 MV·A,如图4所示。在未来某个水平年,系统将增至18个节点,其中7个节点上接有电源,17个节点上有负荷,共有27条待选线路可供扩建。系统支路数据(包括新增线路和原有线路)见表1,发电机出力、负荷功率见表2,各发电机次暂态电抗数据见表3。其中节点18为平衡节点,除节点18外有发电机功率注入的节点均为PV节点,其余节点为PQ节点,负荷功率因数取0.9,输电线路电阻为0.026 Ω/km。假定每条输电线路走廊最多允许的线路数目为4条,限流电抗器的最大阻抗为30 Ω,系统允许投运的限流电抗器数目为5台,要求规划方案系统允许最大短路电流为50 kA,即系统断路器的最大开断电流,系统要求的最低短路电流裕度为10%。参考500 kV并联电抗器造价,假定限流电抗器单位容量投资成本为2.5万元/MV·A[15],限流电抗器额定电流为3 kA,每回输电线路单位长度投资成本为100万元/km[16]。
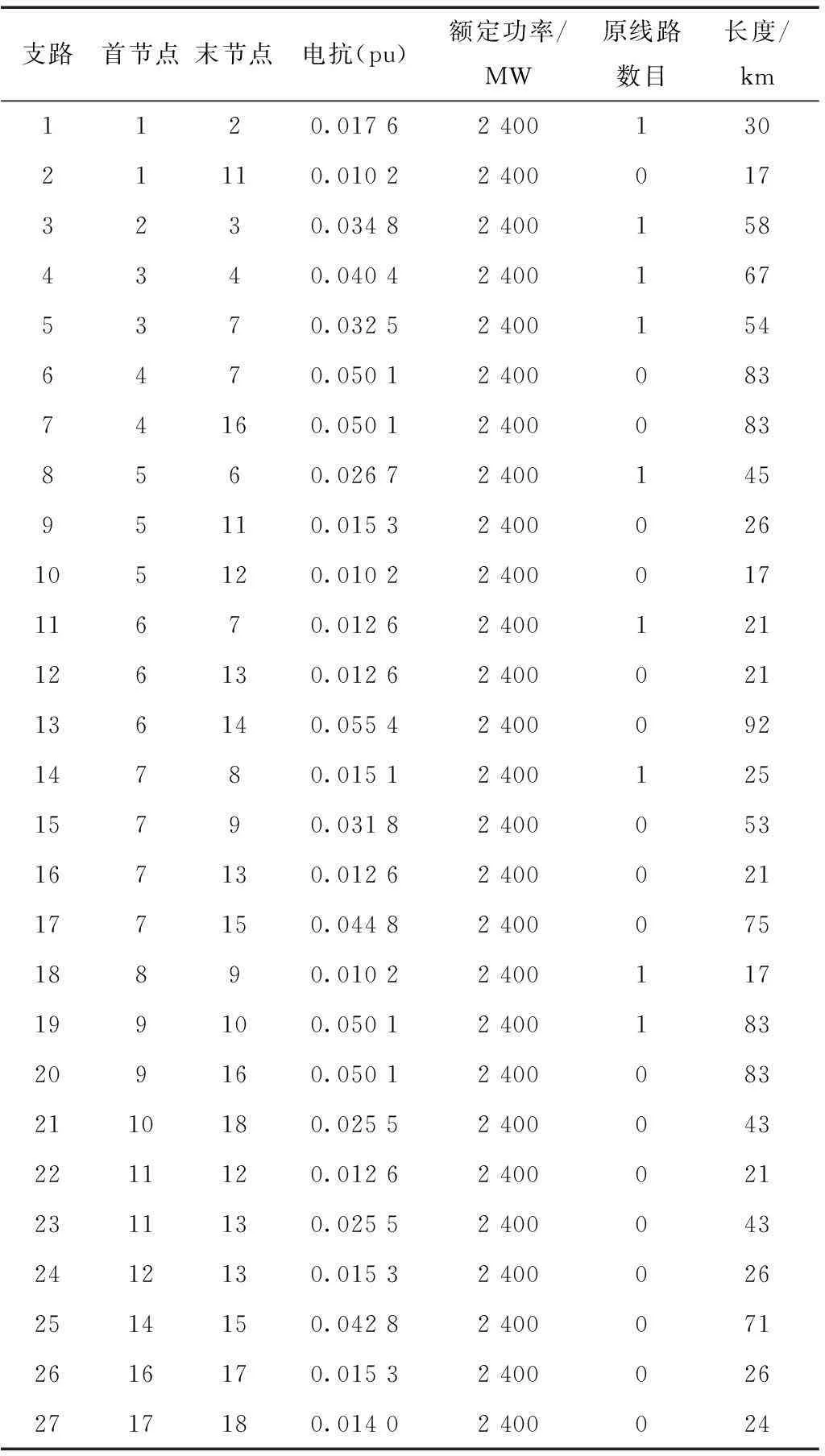
表1 18节点系统支路参数
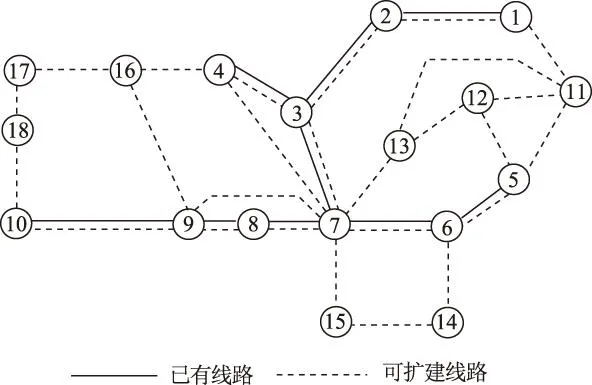
图4 18节点系统Fig.4 18-bus system
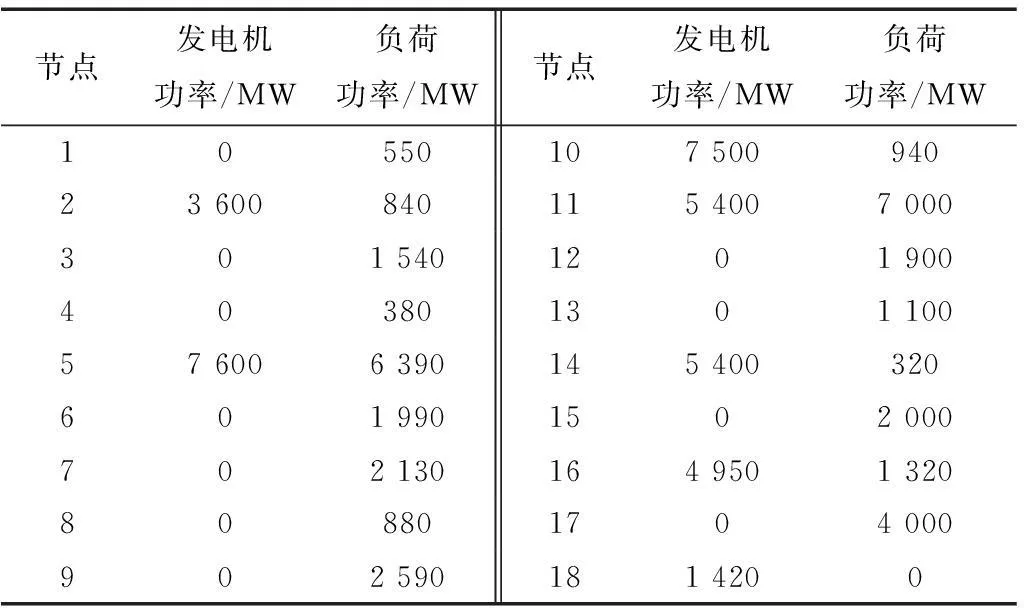
节点发电机功率/MW负荷功率/MW节点发电机功率/MW负荷功率/MW105501075009402360084011540070003015401201900403801301100576006390145400320601990150200070213016495013208088017040009025901814200
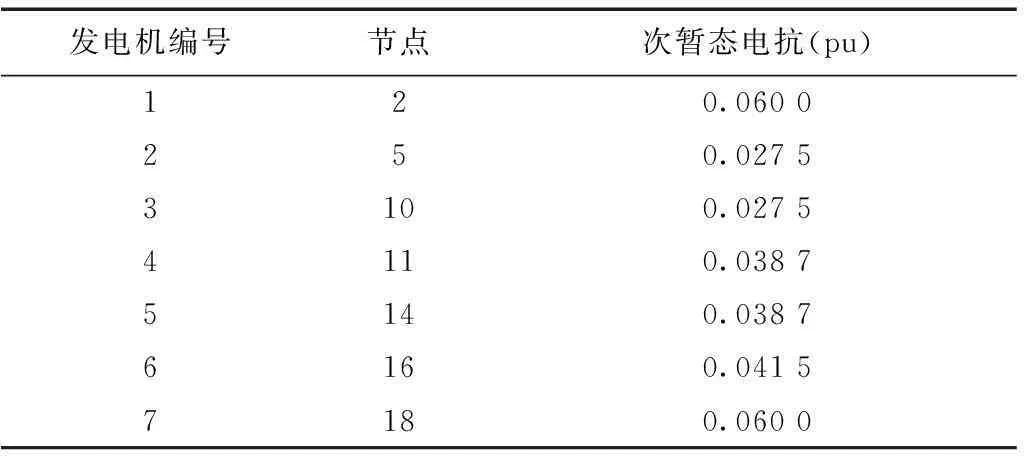
表3 18节点系统等效发电机直轴次暂态电抗数据
下面分3种情况进行分析和讨论:
1)不考虑限流电抗器的应用,仅考虑新建线路求解总投资成本最小的规划方案A,即传统的输电网规划方案。
2)短路电流裕度取10%,采用遗传-粒子群混合算法求解18节点算例下计及短路电流限制的输电网双层扩展规划模型,得到规划方案B。
3)短路电流裕度取20%,18节点算例下计及短路电流限制的输电网双层扩展规划模型得出的规划方案C。
规划方案A、B、C具体结果见表4。
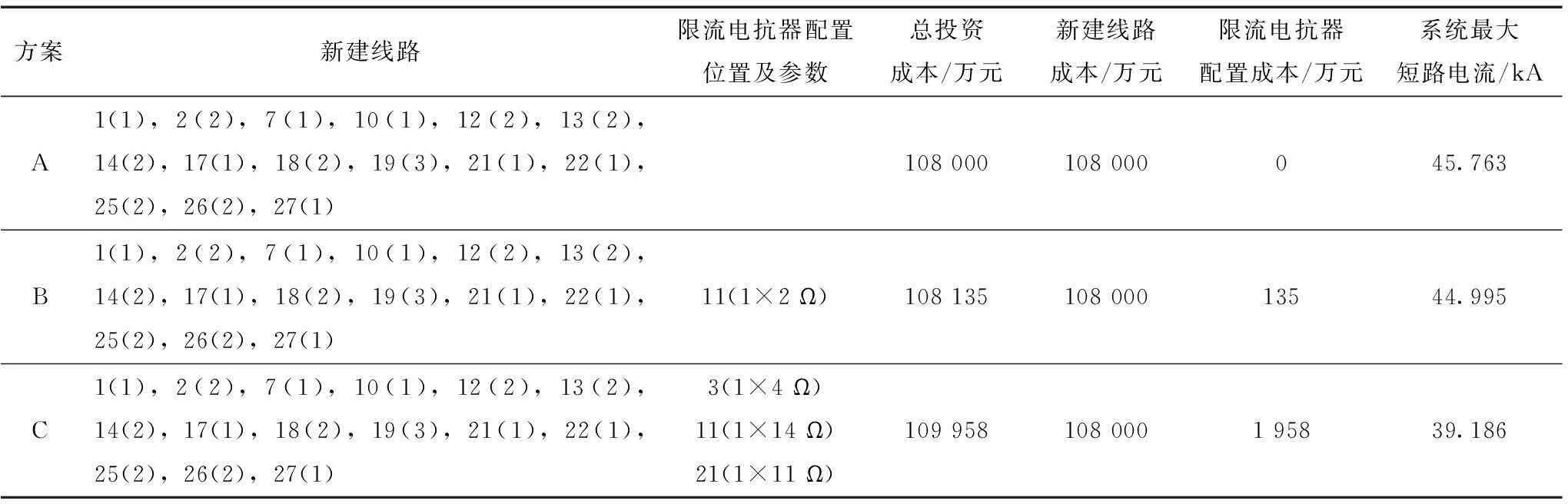
表4 18节点系统3种情况下规划方案比较
表4中新建线路一栏中括号中的数字表示支路新建线路的回数,如2(1)表示支路2新增1回线路,其余类同;限流电抗器配置位置及参数栏中括号中的数字表示支路投运的限流电抗器参数,如11(1×2 Ω)表示支路11的1回线路加装阻值2 Ω的三相限流电抗器,其余类同。
由表4可见,规划方案A与文献[17]给出的方案新建线路总长度一致,但方案A的最大短路电流为45.763 kA,系统短路电流裕度为8.5%,不足10%。
与方案A相比,方案B新建线路结果与方案A一致,但总投资成本增加了135万元,原因是在支路11线路上加装了一组2 Ω的限流电抗器,将系统最大短路电流限制到44.995 kA,满足系统短路电流裕度大于10%的要求。
规划方案C与方案B相比,新建线路结果与新建线路成本一致,由于在支路3、11、21线路上分别加装了4 Ω、14 Ω、11 Ω的限流电抗器,限流电抗器配置成本较方案B高1 823万元,短路电流裕度大于20%。因此,过高的短路电流裕度会增加系统的总投资成本,造成资源浪费。
比较3种方案可知,考虑短路电流限制的双层输电网规划模型在18节点算例场景下求解得出的规划方案B同时满足新建线路成本最小和限流电抗器优化配置成本最小,符合系统规划方案对短路电流水平的要求。
4.219节点测试系统
为进一步说明考虑短路电流限制的输电网双层规划模型与先实施传统输电网规划再进行限流电抗器优化配置的异同,考虑在原有的18节点系统上新增一个负荷节点,构成19节点测试系统,网络拓扑如图5所示。节点19负荷有功功率为1 800 MW,新增4条待选输电线路走廊,其具体参数见表5。

图5 19节点系统Fig.5 19-bus system
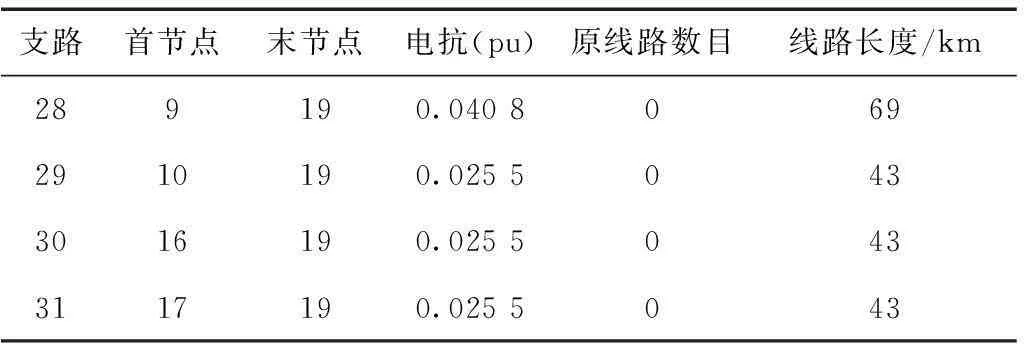
支路首节点末节点电抗(pu)原线路数目线路长度/km289190.04080692910190.02550433016190.02550433117190.0255043
在19节点算例场景下比较本文提出的输电网双层规划模型与传统输电网规划模型得出的规划方案差别,分以下3种情况进行分析讨论:
1)短路电流裕度取10%,采用遗传-粒子群混合算法求解19节点系统中计及短路电流限制的输电网双层扩展规划模型,得到规划方案D如图6所示。
2)不考虑限流电抗器的应用,19节点算例下传统输电网规划模型求解得出的规划方案E。
3)短路电流裕度取10%,在19节点算例下对传统输电网规划模型求解得出的规划方案E进行限流电抗器的优化配置,得出的规划方案F如图7所示。
由表6可见,本文提出的规划方案D与传统的方案E相比,新增输电线路长度长5 km,新建线路成本高500万元;方案D在支路11的一回线上配置4 Ω的限流电抗器,系统最大短路电流限制到44.847 kA,而方案E未配置限流电抗器,系统最大短路电流高达48.476 kA,接近系统断路器最大开断电流50 kA,短路电流裕度为3.05%,严重不足,不符合本文规划要求。
比较规划方案D和先进行传统输电网规划再进行限流电抗器优化配置的方案F,由于新的负荷节点19的出现,方案D在18节点算例得出的传统规划方案A的基础上,在节点17和节点19之间新建了2回线路,在节点17和节点18之间新建了2回线路,共计134 km,在支路11的一回线上配置4 Ω的限流电抗器,共计4 Ω。方案F在方案A的基础上,在节点10和节点19之间新建2回线路,在节点10和节点18之间新建一回线路,共计129 km,在支路11的一回线路上配置了4 Ω限流电抗器,在支路21的两回线路上都配置了8 Ω限流电抗器,共计20 Ω。

图6 规划方案DFig.6 Planning scheme D

图7 规划方案FFig.7 Planning scheme F
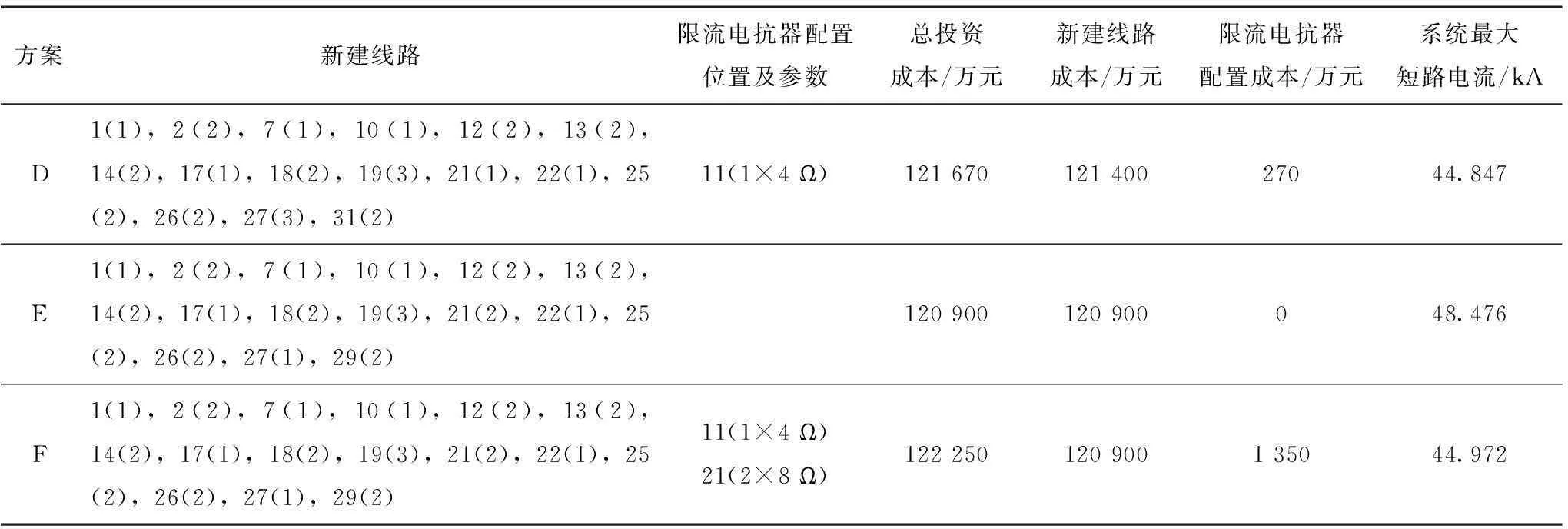
方案新建线路限流电抗器配置位置及参数总投资成本/万元新建线路成本/万元限流电抗器配置成本/万元系统最大短路电流/kAD1(1),2(2),7(1),10(1),12(2),13(2),14(2),17(1),18(2),19(3),21(1),22(1),25(2),26(2),27(3),31(2)11(1×4Ω)12167012140027044.847E1(1),2(2),7(1),10(1),12(2),13(2),14(2),17(1),18(2),19(3),21(2),22(1),25(2),26(2),27(1),29(2)120900120900048.476F1(1),2(2),7(1),10(1),12(2),13(2),14(2),17(1),18(2),19(3),21(2),22(1),25(2),26(2),27(1),29(2)11(1×4Ω)21(2×8Ω)122250120900135044.972
方案D新增输电线路长度比方案F长5 km,新建线路成本高500万元;方案D限流电抗器优化配置成本为270万元,比方案F限流电抗器优化配置成本低1 080万;方案D最大短路电流44.847 kA低于方案F最大短路电流44.972 kA,两个方案短路电流水平均满足规划方案短路电流裕度要求。
从经济方面来看,方案D总投资成本低于方案F,为121 670万元,比方案F低580万元,这是由于方案F选择将节点19的负荷接入节点10,导致节点10短路电流急剧上升,超过45 kA,需要配置限流电抗器来降低该节点短路电流以满足系统短路裕度要求,增加了限流电抗器的配置成本,从而提高了总投资成本。从网架构建方面,方案D的短路电流裕度大于方案F,短路电流水平相对较低,且采用的限流电抗器数目更少,阻抗更小,网损也相对较小。因此,本文模型得出的方案D在网架构建上也更具合理性。
图8为采用遗传-粒子群混合算法重复5次求解19节点系统下考虑短路电流限制的输电网双层扩展规划模型的寻优示意图,最终总投资成本均收敛于同一值,为121 670万元,达到收敛时平均迭代数目为26.6代。
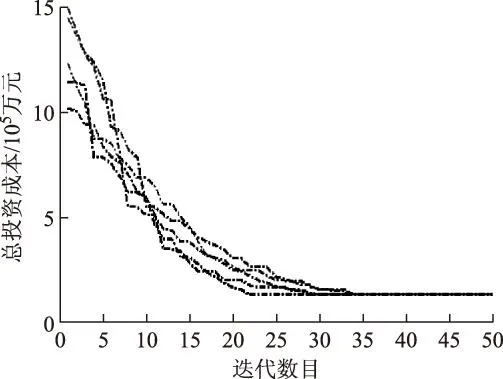
图8 遗传-粒子群混合算法求解双层规划模型收敛性示意图Fig.8 The convergence of mixed GA-PSO algorithm for solving bi-level model
综合以上分析,本文提出的计及短路电流限制的输电网双层扩展规划模型得到的方案更优,遗传-粒子群算法也能较好满足模型求解的需要。
5结论
本文在分析电网短路电流的影响因素及典型限制措施基础上,将限流措施的优化配置引入到输电网规划模型中,以线路建设、限流电抗器优化配置的总投资成本最小化为目标,建立了计及短路电流限制的输电网双层扩展模型。最后,采用遗传-粒子群混合算法对所建的输电网扩展规划模型进行了求解,并通过18节点算例及其扩展算例验证了本文模型和算法的有效性和可靠性。
在输电网扩展规划中考虑限流措施的应用能有效降低规划方案短路电流水平,同时,限流电抗器的优化配置投资也直接影响规划方案新建线路的选择,本文模型得到的规划方案能够兼顾线路投资和限流电抗器投资,实现投资总成本最小,对短路电流水平较高的城市电网进行优化扩展规划具有较高的适用性。
参考文献
[1]阮前途.上海电网短路电流控制的现状与对策[J].电网技术,2005,29(2):78-83.
Ruan Qiantu.Present situation of short circuit current control in Shanghai power grid and countermeasures[J].Power System Technology,2005,29(2):78-83.
[2]郭杰.广州电网短路电流特性及运行对策研究[D].广州:华南理工大学,2013.
[3]徐贤,丁涛,万秋兰.限制短路电流的220 kV 电网分区优化[J].电力系统自动化,2009,33(22):98-101.
Xu Xian,Ding Tao,Wan Qiulan.220 kV power grid district-dividing optimization for limiting fault current[J].Automation of Electric Power Systems,2009,33(22):98-101.
[4]陈丽莉,黄民翔,张弘,等.电网限流措施的优化配置[J].电力系统自动化,2009,33(11):38-42.
Chen Lili,Huang Minxiang,Zhang Hong,et al.An optimization strategy for limiting short circuit current[J].Automation of Electric Power Systems,2009,33(11):38-42.
[5]Vovos P N,Harrison G P,Wallace A R,et al.Optimal power flow as a tool for fault level-constrained network capacity analysis[J].IEEE Transactions on Power Systems,2005,20(2):734-741.
[6]刘凯,陈红坤,林军,等.故障限流器在电力系统中应用研究现状[J].电力系统保护与控制,2010,38(7):147-151.
Liu Kai,Chen Hongkun,Lin Jun,et al.Study situation of applications of fault current limiter in power system[J].Power System Protection and Control,2010,38(7):147-151.
[7]薛敏,卢波,黄华,等.首台500 kV线路串联电抗器在华东电网的应用研究[J].华东电力,2008,36(11):47-50.
Xue Min,Lu Bo,Huang Hua,et al.Application of the first 500 kV series reactors to East China power grid[J].East China Electric Power,2008,36(11):47-50.
[8]GB/T 1094.6—2011.电力变压器第六部分:电抗器[S].
[9]应林志,王建全,陈迅,等.广东电网超高压短路限流器优化配置方案[J].电力系统自动化,2012,36(4):96-100.
Ying Linzhi,Wang Jianquan,Chen Xun,et al.An optimal configuration scheme for ultra-high voltage short-circuit current limiter in Guangdong power grid[J].Automation of Electric Power Systems,2012,36(4):96-100.
[10]黄家栋,罗伟强,赵永强,等.两种新的电网连通性分析快速算法[J].电力系统保护与控制,2008,36(17):16-18.
Huang Jiadong,Luo Weiqiang,Zhao Yongqiang,et al.Two new high-speed algorithms for electrical network connectivity analysis[J].Power System Protection and Control,2008,36(17):16-18.
[11]玄光男.遗传算法与工程设计[M].北京:科学出版社,2000.
[12]陈丽莉,黄民翔,许诺,等.考虑潮流约束的限流措施优化配置[J].高电压技术,2010,36(6):1572-1576.
Chen Lili,Huang Minxiang,Xu Nuo,et al.Optimal strategy for short-circuit current limiters deployment considering power flow[J].High Voltage Engineering,2010,36(6):1572-1576.
[13]袁晓辉,苏安俊,聂浩,等.面向启发式调整策略和粒子群优化的机组组合问题[J].电工技术学报,2009,24(12):137-141.
Yuan Xiaohui,Su Anjun,Nie Hao,et al.Unit commitment problem based on PSO with heuristic-adjusted strategies[J].Transactions of China Electrotechnical Society,2009,24(12):137-141.
[14]王锡凡.电力系统优化规划[M].北京:水利电力出版社,1990.
[15]国家电网公司.国家电网公司输变电工程典型造价:500 kV变电站分册[M].北京:中国电力出版社,2006.
[16]国家电网公司.国家电网公司输变电工程典型造价:500 kV输电线路分册[M].北京:中国电力出版社,2006.
[17]郑静,文福拴,李力,等.计及能效电厂优化配置的输电系统两层规划[J].电力自动化设备,2013,33(6):13-20.
Zheng Jing,Wen Fushuan,Li Li,et al.Two-level planning of transmission system with optimal placement of efficiency power plants[J].Electric Power Automation Equipment,2013,33(6):13-20.
宋柄兵男,1990年生,硕士,研究方向为电力系统规划。
E-mail:songbingbing1119@163.com(通信作者)
顾洁女,1971年生,副教授,研究方向为电力系统规划、电网大数据分析。
E-mail:gujie@sjtu.edu.cn
A Bi-Level Expansion Planning Model of Transmission Systems Considering Short-Circuit Current Constraints
SongBingbing1,2GuJie1,2
(1.Key Laboratory of Control of Power Transmission and ConversionMinistry ofEducation Shanghai Jiaotong UniversityShanghai200240China 2.School of Electronic Information and Electrical EngineeringShanghai Jiaotong University Shanghai200240China)
AbstractWith the consideration of optimal configuration of short-circuit current limiting measures in typical power system transmission planning, a bi-level planning model is developed for transmission system. The upper level model takes the minimum total cost of the transmission line and the current limiting reactor investments as its objective. Given the transmission line construction scheme derived by the upper model, the lower level model takes the minimum cost of the current limiting reactor investment as its objective. With the interaction between two levels, the overall planning scheme which includes transmission line construction scheme and current limiting reactor configuration scheme is finally determined by the upper model. A algorithm combining the genetic algorithm and the particle swarm algorithm is adopted to solve the proposed bi-level planning model. Results of the case study for an 18-bus system and its expanded system verify the feasibility and efficiency of the proposed model and algorithm.
Keywords:Transmission expansion planning, short-circuit current margin, optimal configuration of current limiting reactor, bi-level optimization, hybrid optimization algorithm
作者简介
中图分类号:TM715
收稿日期2015-02-08改稿日期2015-11-01
“十二五”国家科技支撑计划重大项目资助(2013BAA01B04)。

