船载稳定平台运动学分析与仿真

付彦琨,吴恩启,徐紫红,应峥嵘

(上海理工大学 机械工程学院,上海　200093)



船载稳定平台运动学分析与仿真

付彦琨,吴恩启,徐紫红,应峥嵘

(上海理工大学 机械工程学院,上海200093)

摘要根据船舶航行特点,提出了一种船载框架式稳定平台,以隔离海浪波动对船载仪器的影响。对稳定平台进行运动学分析,建立了纵摇框架和驱动电机之间运动的数学模型,通过求解数学模型,确定出两者之间最优运动线性关系;利用空间矩阵法推导出稳定平台执行端边界点的位置方程,得到稳定平台的工作空间;对稳定平台进行运动仿真,仿真结果验证了稳定平台设计的合理性和可靠性。

关键词稳定平台;位置方程;运动学分析;建模仿真

船舶在海洋中航行时,受到风浪的影响,会产生具有一定幅值与频率的波动,使得船载设备和仪器产生不同程度的纵摇及横摇运动,从而制约其工作性能,因此需要借助船载稳定平台隔离这种扰动的影响[1-2]。常用的船载稳定平台主要由执行端、基体和液压驱动系统组成,是以Stewart平台为基础发展而来的[3],属于多自由度并联机构。多自由度并联机构的高承载力和高动态性虽然能满足使用要求,但在动力学和控制方面仍存在许多问题[4-6]。动力学方面,位置正解的复杂性会增加初期的计算量,从而使设计周期变长。控制方面,需解决的冗余驱动输入引起的冗余力和运动耦合效应对机构工作精度的影响[7]。近年来,国内外对并联机构的研究,集中在降低位置正解复杂性和研究提高机构工作性能的控制策略等方面,取得了一定进展,但主要针对六自由度并联机构[8-10],对少自由度并联机构研究处于发展阶段。

为降低稳定平台的控制难度和运动误差,文中提出了一种船载稳定平台的设计方法,该平台采用并联框架结构,简化了整体结构的复杂性,利用伺服电机和滚珠丝杠组件代替液压系统作为驱动源,在保证运动精度的前提下,降低了平台的控制难度。通过对稳定平台的数学模型和三维模型进行计算分析,验证了该稳定平台的设计可行性和合理性。

1原理

1.1稳定平台的结构组成

稳定平台为并联双框架结构,包括纵摇框架、横摇框架、基体、执行端、滑块、连杆、滚珠丝杠和伺服电机,如图1所示。纵摇框架由伺服电机通过滑块和连杆间接进行驱动,围绕转动副C和D进行纵向俯仰运动。横摇框架是转动副和杆件构成的平面四杆机构,由伺服电机直接进行驱动,围绕转动副E和F进行横向摇摆运动。另外,基体直接与船体固连,执行端为稳定平台的输出端,通过转动副H、I与横摇框架相连,其运动是纵向俯仰和横向摇摆两个运动的合成。当船舶在风浪中航行时,稳定平台能对船舶纵摇和横摇两个方向的扰动进行补偿,实现隔离风浪扰动的功能。

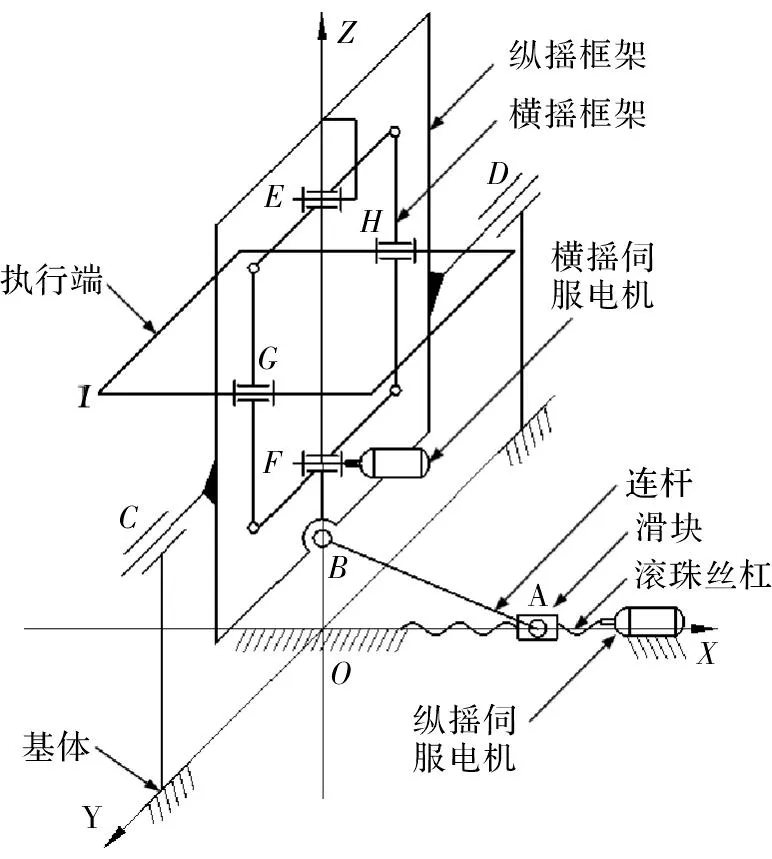
图1　稳定平台的设计原理图

1.2稳定平台的自由度计算

稳定平台机构的自由度可用多环闭链机构的自由度计算公式求解[11]。

(1)其中,P为运动副的总数;fi为第个运动副的自由度;L为机构中封闭链的个数;λj为第j个封闭链的自由度;fp为消极自由度;ft为局部自由度。经计算可知,该机构的自由度数F=2,与机构的动力源数相等,不存在自由度冗余。

2稳定平台运动学分析

2.1线性关系的确定

为便于分析执行端的运动,首先对其运动进行简化。在基体设定坐标系O-XYZ,在执行端设定坐标系O1-X1Y1Z1如图2所示。其中,α表示杆L1与X轴的夹角,β、γ分别表示纵摇框架和横摇框架的角位移。γ由伺服电机直接驱动,β是伺服电机通过滑块和连杆进行控制,在图2中体现为,滑块在X向的位移S转换为L2杆绕C点的转动。为使β在一定角度范围内匀速变化时,伺服电机的转速易于控制,以便实现位移S和角位移β之间等速转换,因此需选择合适的L1和L2杆长来满足以上要求。由图2中的关系可得

L3=L1sinα+L2cosβ

(2)

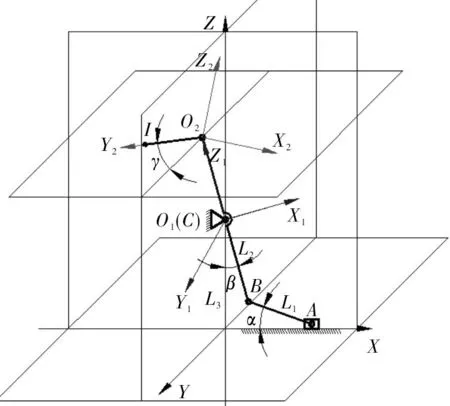
图2　稳定平台运动简图

滑块在X向的位移s为

(3)

滑块在X向的速度v为

(4)

滑块A在X向的加速度

(5)

将上述数学模型转化为

(6)

取L3=1 000 mm,β=10°,由公式可求得L1=0.25 m,L2=0.95 m。

由以上计算结果可求得滑块在X向位移s,速度v与稳定平台纵向俯仰运动角位移β之间的关系,如图3所示。

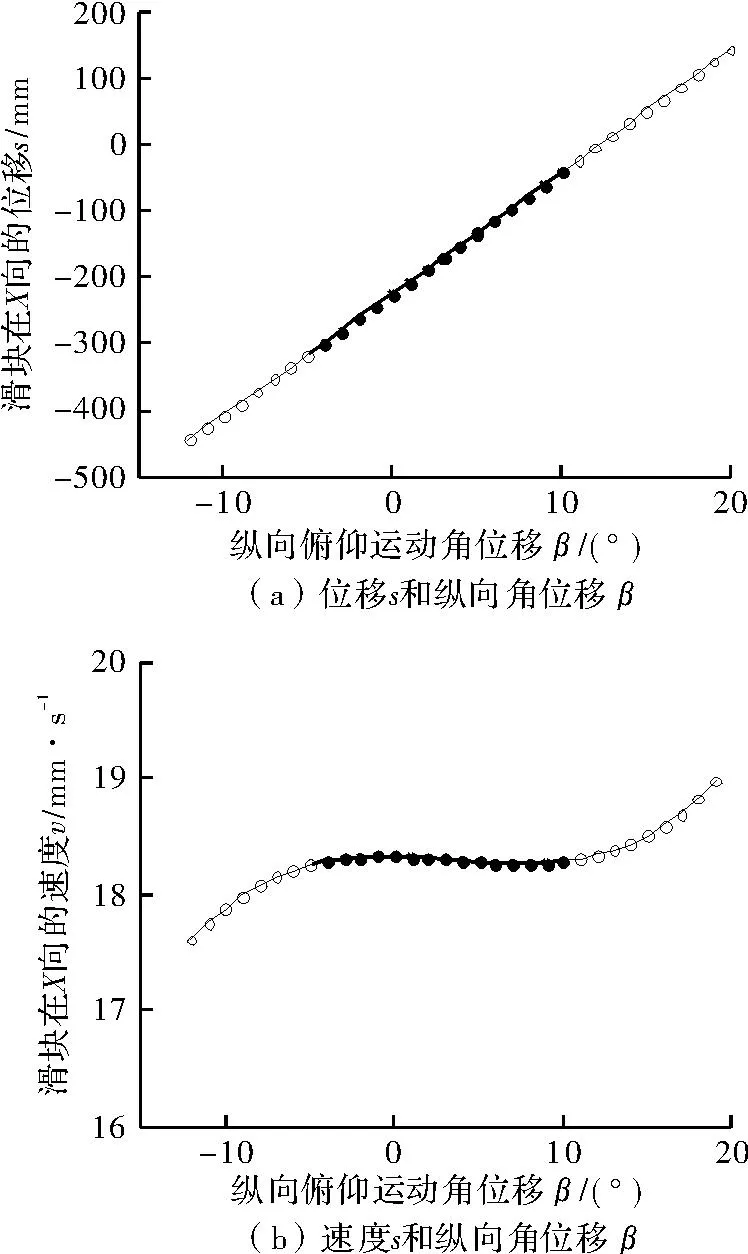
图3　位移、速度与执行端纵向角位移的关系

由图3(a)可知,当滑块在X向匀速运动时,β在一定角度范围内匀速变化。此时,滑块在X方向的位移s和执行端纵向角位移β之间呈近似线性关系,可实现两者之间的等距转化;由图3(b)可知,稳定平台纵向位移角β在(-5°,10°)范围内变化时,滑块在X方向的速度v波动最小,可近似为匀速运动,在此角度范围内β的线性误差为每度0.18%。

2.2稳定平台位置解析

执行端为稳定平台的输出端,其边界点的运动轨迹可表示该稳定平台输出端的最大工作空间。横摇方向的运动关于XOZ面对称,所以取执行端一侧边界上的点I,研究该点的运动轨迹。根据框架稳定平台坐标系定义[12],取与基体固连的坐标系OXYZ,与纵摇框架固连的坐标系O1X1Y1Z1,与横摇框架固连的坐标系O2X2Y2Z2。用β和γ分别表示坐标系O1X1Y1Z1,O2X2Y2Z2与坐标系OXYZ之间的相对位置关系,如图2所示。

坐标系OXYZ通过旋转和平移后得到坐标系坐标系O1X1Y1Z1,对应的其次旋转矩阵和位移矩阵分别为Rot(Y,β)和Trans1。坐标系O1-X1Y1Z1通过旋转和平移后得坐标系O2X2Y2Z2对应的其次旋转矩阵和位移矩阵分别为Rot(X1,γ)和Trans1。图2中的点I为执行端边界点,其在OXYZ坐标系的坐标为Ixyz可表示为

Ixyz=Pxyz×Ix1y1z1

(7)

其中,Pxyz为I点由OXYZ～O1X2Y2Z2的变换矩阵;Ix2y2z2为I点在O2X2Y2Z2坐标系内的坐标

Pxyz=Trans1(0,0,L3)×Rot(X,β)×Trans2(0,0,L2)×

(8)

仿真得到执行端边界点I的运动范围,如图4所示。

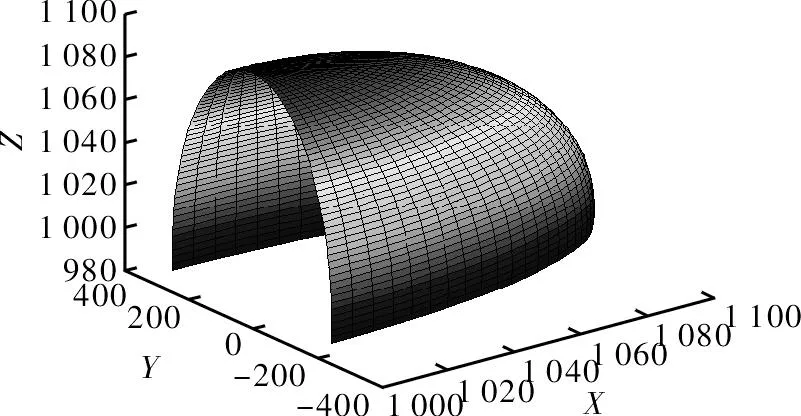
图4　边界点I的运动范围

3稳定平台的仿真

因船舶甲板上可使用的空间有限,船舶搭载稳定平台的数量会受到限制。文中设计的稳定平台能同时安装多个执行端以满足使用要求,从而大幅提高稳定平台的空间利用率。通过三维建模软件SolidWorks建立稳定平台的模型如图5所示。

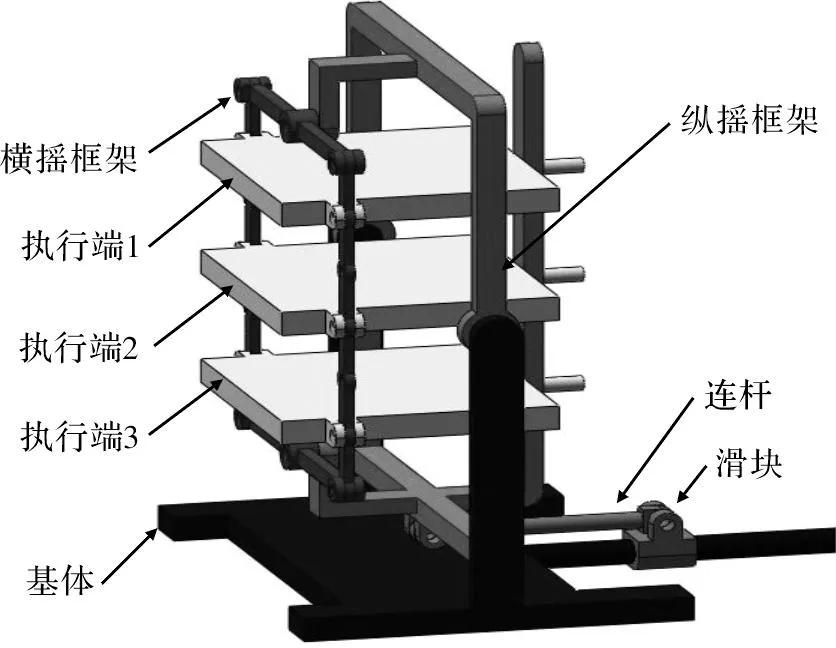
图5　稳定平台三维仿真模型

为进一步验证滑块位移和纵向角位移之间的运动关系,并确定稳定平台的运动误差,利用虚拟仿真软件对稳定平台进行实体仿真分析。船舶受到海浪的扰动后,稳定平台跟随船舶在纵摇和横摇方向分别进行俯仰和摇摆运动,使执行端保持在初始工作角度,设船舶在4级海况下航行,把海浪的扰动简化为正弦波动[13],周期为10s,幅值为10°,并设执行端初始工作角度为0°。可得到滑块X向位移s和纵摇位移角β的关系,如图6所示。稳定平台执行端在运动过程中与初始角度的误差,如图7所示。

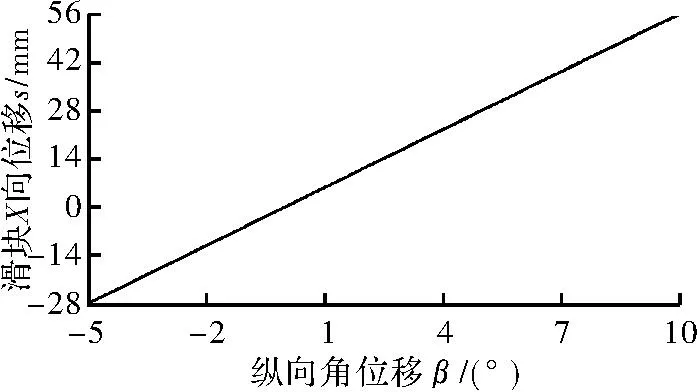
图6　滑块X向位移s和纵摇位移角β的关系

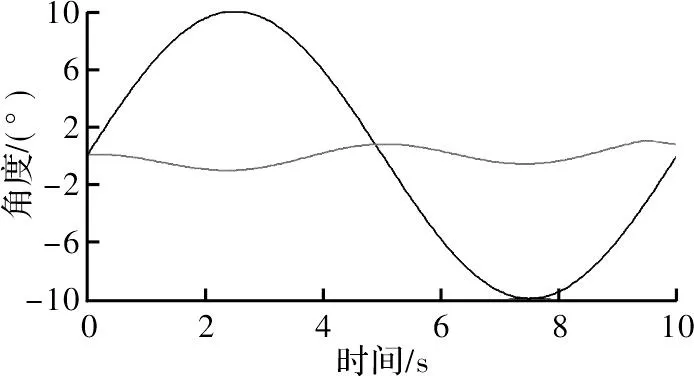
图7　稳定平台运动误差

由图6仿真结果可知,稳定平台在运动过程中,滑块在X向位移和纵向角位移β呈线性关系,与理论求解结果一致。由于纵摇和横摇框架在运动过程中存在运动耦合效应,对修正纵摇和横摇方向角度变化有一定的影响,从而导致执行端与初始工作角度产生一定的误差。由图7可知,执行端与初始角度的误差<0.7°。仿真结果说明,稳定平台基本能消除船舶纵横摇扰动。

4结束语

文中设计的船载稳定平台,采用框架式的构造,简化了整体的结构,提高了空间利用率。对稳定平台进行运动学分析后,确定了滑块位移与稳定平台纵向俯仰运动角位移之间的线性关系,并通过求解执行端边界点的空间位置方程,得到稳定平台的工作空间。另外,采用伺服电机和滚珠丝杠组件替代液压系统对机构进行驱动,在满足使用要求的基础上,降低了运动耦合效应的影响和稳定平台的控制难度。通过实例仿真,验证了稳定平台设计的有效性和合理性,为同类机构的研究提供了一定的依据。

参考文献

[1]王亚东,袁绪龙,张宇文,等.波浪对导弹垂直发射水弹道影响研究[J].兵工学报,2012,33(5):630-635.

[2]段齐骏,张福祥.船载多管火箭武器系统发射姿态控制对策[J].南京理工大学学报,2002,26(6):595-598.

[3]陈学生,陈在礼,孔民秀.并联机器人研究的进展与现状[J].机器人,2002,24(5):464-470.

[4]冯志友,李永刚,张策,等.并联机器人机构运动与动力分析研究现状及展望[J].中国机械工程,2006,17(9):979-984.

[5]SuHJ,DietmaierP,McCarthyJM.Trajectoryplanningforconstrainedparallelmanipulators[J].JournalofMechanicalDesign,2003,125(12):709-715.

[6]KongMX,YouW,DuZJ,etal.Optimaldesignfora2-DOFhighdynamicmanipulatorbasedonparallelogrammechanism[C].Beijing:IEEEInternationalConference,2000.

[7]刘晓,赵铁石,边辉,等.耦合型3自由度并联稳定平台机构动力学分析[J].机械工程学报,2013,49(1):45-52.

[8]KimWK,ByunYK,ChoHS.Closed-formforward-positionsolutionfora6-DOF3-PPSPParallelmechanismanditsimplementation[J].TheInternationalJournalofRoboticsResearch,2001,20(1):85-99.

[9]ChenCT,PhamHV.Trajectoryplanninginparallelkinematicmanipulatorsusingaconstrainedmulti-objectiveevolutionaryalgorithm[J].SpringerScienceBusinessMedia,2012(67):1669-1681.

[10]郭宗和,李连升,孙术华.3—RPC并联机器人的运动轨迹规划与仿真[J].中国机械工程,2007,18(9):1036-1038.

[11]SaeedBNiku.机器人学导论—分析、控制及应用[M].2版.孙富春,朱纪洪,刘国栋,等,译.北京:电子工业出版社,2013.

[12]单家元,王肇敏,魏华梁.内旋三轴转台框架系统建模[J].计算机仿真,2002,19(3):5-7.

[13]姜礼平,王玉珍,胡伟文.风浪中船舶横摇仿真与预报研究[J].控制工程,2013,20(2):344-347.

Kinematic Analysis and Simulation of Ship-borne Stable Platform

FU Yankun,WU Enqi,XU Zihong,YING Zhengrong

(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

AbstractA ship-borne stable platform is developed to eliminate the influence of the waves based on the characteristics of ship navigation.The linear relationship of the pitch part and drive motor is found by solving the mathematical model of movement between the pitching frame and drive motor.Then the workspace of the platform is obtained.Finally,a motion simulation on the platform is established,and the results show that the design of the platform is rational and feasible.

Keywordsstable platform;position equation;kinematic analysis;simulation

中图分类号TH112

文献标识码A

文章编号1007-7820(2016)04-059-04

doi:10.16180/j.cnki.issn1007-7820.2016.04.016

作者简介:付彦琨(1988—),男,硕士研究生。研究方向:CAD/CAE/CAM。吴恩启(1972—),男,博士,副教授,硕士生导师。研究方向:CAD/CAE/CAM。

收稿日期:2015- 09- 15