基于统计模型的图像融合

袁一鸣，高文根，江 明（安徽工程大学电气工程学院，安徽芜湖 241000）



基于统计模型的图像融合

袁一鸣，高文根，江 明
（安徽工程大学电气工程学院，安徽芜湖 241000）

摘要：永磁电机是电动汽车的主要部件之一，其可靠性关系着汽车的整体性能指标．以奇瑞集团永磁电机检测生产线为工况背景，通过大量理论分析和现场试验，提出了一种新的红外与可见光图像融合算法，对源图像小波系数进行广义高斯统计建模的多模态图像融合，采用新的加权平均融合规则来进行小波系数的融合，通过数据估计特征指数和形状参数，判断融合数据是否在广义高斯或对称α稳定的吸引域内；最后，将融合后的系数重构为一幅图像，比较基于这两种统计模型下融合图像的效果．实验结果证明，基于广义高斯小波系数建模的加权平均法融合的效果比较好．

关 键 词：图像融合；广义高斯分布；对称α稳定分布；双树复小波变换

永磁电机是电动汽车的关键部件，它的性能好坏直接影响到汽车性能．在电动汽车工业的科研领域，提高永磁电机的工作可靠性始终是电动汽车研究的前沿课题．目前判断电机故障缺陷的一种方法是红外成像技术，该技术是利用可见的热分布图像得到热像图，然后根据红外热像图的变化情况判断电机可能具有的不良状态或缺陷．然而，红外图像不能反应实物真实场景，将红外图像与可见光图像融合作为热源主要辨识依据，可以改善两者局限性．而手持式红外检测仪需要工作人员手持巡视监测电机，因而不可能对各个待测电机同时进行在线监视，因此，采用轮巡机械云台搭载可见光和红外相机进行轮巡，将采集到的可见光图像和红外图像传送至监控中心进行融合处理．红外与可见光的图像融合已经得到广泛研究，除此之外，目前的图像融合方法还有很多，可以简单分为两类：像素级融合和区域级融合．尽管多数像素级融合方法是有效的，但它们不是在严格的数学推导下得到的，近年来，逐渐有严格的方法被提出，包括基于估计理论的方法．Sharma提出贝叶斯融合方法［1］假设多分辨率图像表示服从高斯分布，Achim提出了基于非高斯建模的图像融合方法［2］，证明对称α稳定可以对小波系数进行建模．对源图像进行双树复小波变换，为得到更适合的统计模型假设，对加权平均法进行修正，采用梅林变换理论估计融合算法的统计参数．

1 双树复小波变换基本理论

双树复小波变换（DT－CWT）由Nick Kingsbury［3］提出，它可以由小波变换（DWT）得到，通过两棵离散小波树并行实现，一树实现变换的实部，一树生成变换的虚部，两棵树分别作用于图像的行和列上，产生了双树结构［3－4］．每一级分解得到2个低频子带及6个不同方向（±15°、±45°、±75°）的高频细节子带，比小波变换有更多的方向选择性，可提高图像分解与重构的精度并能保留图像的细节信息，而且有限数据冗余，对于m维信号冗余仅为2m：1．

2 小波子带系数建模

2．1 广义高斯分布

Simoncelli在文献［5］中提出广义高斯密度函数为

其中，Γ（·）为众所周知的伽马Gamma函数，即

式（1）中，s是概率密度函数峰值的宽度模型（标准差），p反比于峰值下降率．通常s记为尺度函数，p为形状函数，p越小，相应的广义高斯密度分布尾部越长．若p＝1，则GGD模型退化成拉普拉斯分布；若p＝2，则高斯模型退化成高斯分布［6］．

2．2 α稳定分布

选用SαS作为信号的统计模型是因为稳定随机变量满足稳定性［7］，其稳定变量的线性组合也是稳定的，而且对于独立同分布变量的归一化和，其唯一可能的非平凡极限是稳定的．SαS分布用它的特征函数来定义，即

式中，α为特征指数，取值范围0＜α≤2；δ（－∞＜δ＜∞）为位置参数；γ（γ＞0）为SαS分布的分散度．特征指数是SαS分布参数最重要的一个，它决定分布的形状．α值越小，SαS密度的拖尾就越长．这表明SαS分布中小特征指数的随机变量具有高冲激性．α＝2的稳定过程是高斯过程，α＝1的稳定过程是柯西过程．

2．3 建模结果

为了检验广义高斯分布函数和稳定分布函数是否能够对图像的DT－CWT框架下的系数建模提供恰当的分析手段，首先，利用正态概率分布图，对数据是否属于正态分布以及是否有重尾分布进行评估．然后，通过数据估计形状参数p和特征指数α，判断数据是否在广义高斯或者稳定的吸引域内．采用最大似然法（Maximum Likelihoo，ML）给出可靠的估计结果和最小的置信区间．为了进一步判断稳定性，采用概率密度图显示统计模型匹配数据模式和分布拖尾的程度．同方向可见光和红外图像DT－CWT分解下的正态概率图如图1、图2所示．由图1、图2可知，实线表示样本中每个点的经验概率与数据值的关系，直的虚线表示高斯线，实线并不与高斯线一致，因此，这些数据不符合正太假设．可见光图像与红外图像拟合经验分布分别如图3、图4所示．由图3、图4可知，虚线对应的是广义高斯密度函数拟合经验分布，实线对应的是SαS概率密度函数拟合经验分布，点画线对应的是经验概率密度函数．从图1～图4中可以明显看出这两种重尾分布模型的合理性．

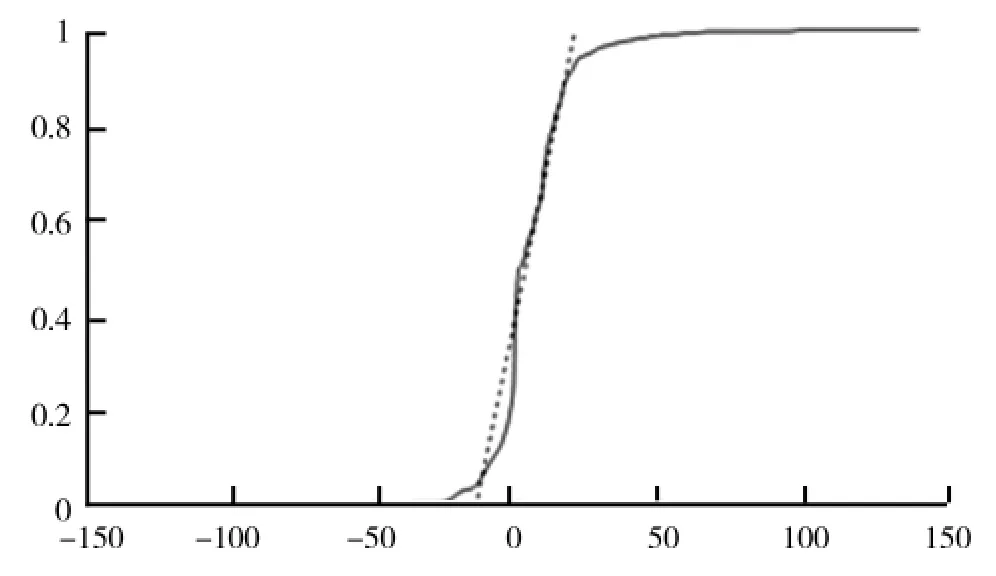
图1　同方向可见光图像正态概率图　

图2　同方向红外图像正态概率图

3 基于两种统计模型的图像融合

3．1 图像融合步骤

永磁电机的可见光图像与红外热图经过DT－CWT分解以后，采用改进的加权平均方法进行各系数的融合，其中权重系数数值由基于梅林变换估计出的GGD模型和SαS模型的参数来计算，最后将融合的系数进行重构．融合步骤［8］如下：

（1）用DT－CW对可见光和红外图像进行分解．

（2）对每组对应的高频系数对X，Y．①计算显著特征度量σx和σy；②计算匹配系数，即

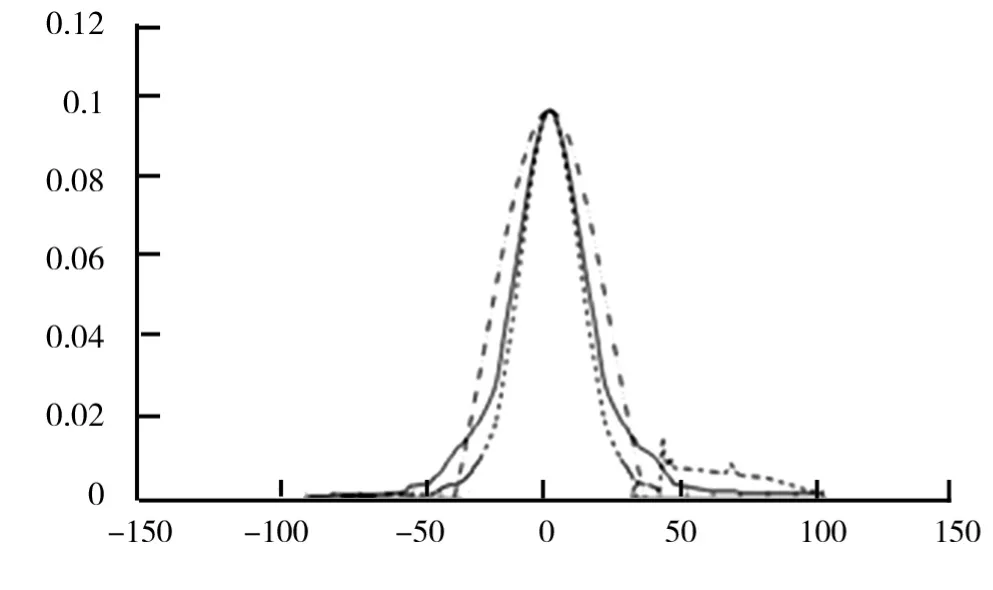
图3　可见光图像拟合经验分布　

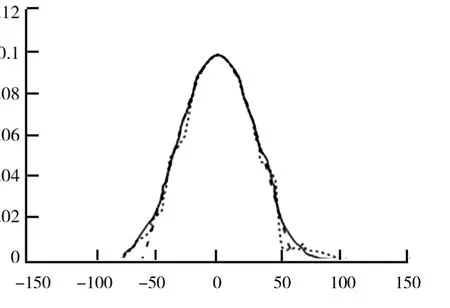
图4　红外图像拟合经验分布

其中，σxy为X和Y之间的协方差；③用公式Z＝WXX＋WYY计算融合系数；

（

3）对低频系数采用平均方法．

（4）将融合后的高频系数和低频系数重构成一幅融合图像．通过以上的融合过程可以看出，整个融合规则由两个计算量决定，匹配系数决定利用哪个模式，即是最大还是最小．显著特征度量决定将小波系数对中的哪个系数值提取到融合系数当中，或者是为该系数赋予更大的权重值．此方法中用对GGD和SαS的适应性估计作为显著特征度．

3．2 基于梅林变换的显著性估计

（1）梅林变换．函数f的梅林变换［9］为：

逆变换为

式中，z为变换的复数变量．与基于傅里叶变换推到统计学参数类似，对于一个随机变量x～p（x），第二类统计函数可以在梅林变换的基础上定义．

第二类第一特征函数为

第二类第二特征函数为

r阶第二类累积量为

（2）广义高斯模型的对数矩估计．假设x＝（x1，x2，…，xn）是GGD的总体X的一个样本．将广义高斯概率密度函数表达式（1）代入式（6），可得

和

它是广义高斯密度的第二类第二特征函数．计算得到一阶和二阶第二类累积量分别得

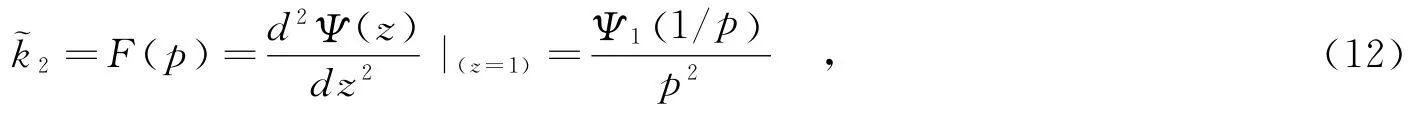
（3）SαS的对数矩估计．Zolatarev指出傅里叶变换和梅林变换存在如下关系

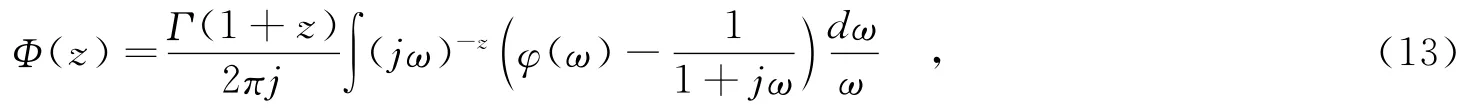
将SαS概率密度函数表达式（2）代入式（13），可得SαS密度的第二类第一特征函数为

假设x＝（x1，x2，…，xn）是SαS总体X的一个样本，根据式（7）、式（8）、式（14）得到SαS模型第二类累积量

4 实验结果与质量评价

实验中采用的图像是奇瑞公司电动汽车永磁电机工作状态的照片．电机红外图像如图5所示．电机可见光图像如图6所示．基于SαS模型融合的图像如图7所示．基于GGD模型融合的图像如图8所示．融合图像的质量评价主要采用以下3种质量评价指标：①熵：融合图像中所包含的信息量，熵值越大说明融合效果越好；②空间频率：反应图像全面活跃水平，越大图像越清晰；③反应了图像像素值的分布情况，标准差越大，图像包含越多的信息．从仿真结果可以看出，基于两种模型的融合都较好地提取了红外图像和可见光图像的信息．基于两种模型融合的熵、空间频率和标准差的具体数据如表1所示．由表1可以看出，基于GGD融合的效果优于基于SαS的融合效果．

图5　电机红外图像　

表1　两种分布模型融合图像质量

5 结论

提出新的基于统计模型的图像融合方法，引入了梅林变换的显著性和匹配测度，得到一种新颖的基于对数尺度随机变量方差的估计器．融合结果表明，两种模型融合效果均可有效检测特征，并且较好保留输入图像的显著特征，其中基于GGD的融合效果更好．

图7　基于SαS模型融合图像　

图8　基于GGD模型融合图像

参考文献：

［1］ R Sharma，M Pavel．Adaptive and statistical image fusion［J］．Society for Information Display Digest，1996，17（5）：969－972．

［2］ A Achim，C N Canagarajah，D R Bull．Complex wavelet domain image fusion based on fractional lower order moments ［A］．In Proceedings of the 8th International Conference on Information Fusion（Fusion 2005），USA：Philadelphia，PA，2005：25－29．

［3］ N G Kingsbury．Image processing with complex wavelets［J］．Philosophical Transactions of the Royal Society of London A，1999（357）：2 543－2 560．

［4］ N G Kingsbury．Complex wavelets for shift invariant analysis and filtering［J］．Applied and Computational Harmonic A－nalysis，2001（10）：234－253．

［5］ S G Mallat．A theory for multiresolution signal decomposition：The wavelet representation［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，1989（11）：674－692．

［6］ 张秀琼．使用统计模型的动态红外和可见光图像融合［J］．计算机工程与应用，2009，45（33）：165－167．

［7］ G Samorodnitsky，M S Taqqu．Stable non－gaussian random processes：stochastic models with infinite variance［J］．Jourral of the American Statistical Association，1995，90（430）：805－806．

［8］ 张红英．统计建模方法在图像融合中的应用研究［D］．无锡：江南大学，2014．

［9］ Tania Stathaki．Image Fusion：Algorithms an Applications［M］．London：Academic Press，2008．

Image fusion based on statistical model

YUAN Yi－ming，GAO Wen－gen，JIANG Ming
（College of Electrical Engineering，Anhui Polytechnic University，Wuhu 241000，China）

Abstract：As a very important component of the electric vehicle，magneto electric machine has as a significant impact on the performance of electric vehicle power train system．This research is based on detection of magneto electric machine in Chery Company．An image fusion algorithm based on Statistical model is proposed for infrared and visible image．This approach is based on fusion rules with proposed weighted average．Simulation experiments show that fusion image with GGD model has a better fusion result．

Key words：image fusion；GGD；SαS；DT－CWT

作者简介：袁一鸣（1982－），女，安徽池洲人，讲师，硕士．

基金项目：安徽检测技术与节能装置省级实验室开放研究基金资助项目（KZ00415004）

收稿日期：2015－09－25

文章编号：1672－2477（2016）01－0038－05

中图分类号：TP

文献标识码：A