基于帕累托最优配电系统多目标规划研究
刘一涛,张 楠,姜 涛,王 征
(国网辽宁省电力有限公司,沈阳 110006)
基于帕累托最优配电系统多目标规划研究
刘一涛,张 楠,姜 涛,王 征
(国网辽宁省电力有限公司,沈阳 110006)
基于供电可靠性的帕累托最优曲线思想,结合帕累托曲线特点,依据算法流程实现公司整体最优投资的选取,解决并找出公司整体对应供电可靠性最优的投资及效益最大化方案,并针对可靠性规划中可靠性与费用关系问题,提出可行性建议。
配电系统;帕累托最优;最优投资;可靠性规划
目前我国传统的电网智能化技术和电网自动化技术的发展,尚不能满足如今电网建设的需要[1]。因此,有必要在传统可靠性规划思路的基础上,制定电力设备寿命长达50年的目标,分远期、中期、近期三个阶段,对未来配电网增长趋势进行预测,以满足人们对电网要求越来越高,电网损耗越来越低的需求。
1 基于供电可靠性的帕累托最优曲线思想
基于可靠性的配电网规划是一个典型的多目标、多约束的优化问题,其目标函数可以包括配电网建设投资最小、可靠性提升成本效益最高、配电网损耗最小、负荷转供能力最强等。
在多属性规划中可有多个属性,如可靠性、费用等。Pareto优化曲线可显示多属性情况下的分析结果,例如电力企业在对系统进行扩展或运行时,Pareto优化曲线可显示不同方案的费用与可靠性之间的关系。因此,Pareto曲线可为电力企业提供选择,并且可对两个属性进行权衡,但是该曲线没有清楚地表示该做出哪个决定[2-3]。
2 Pareto最优曲线
配电系统可靠性规划通常着眼于现实以下两个目标之一[4]:(1)电力企业希望以尽可能低的费用达到某一可靠性目标;(2)电力企业希望在某一预算限值内实现尽可能高的可靠性。
这是一个典型的多目标多约束的优化问题,其目标函数可以包括配电网建设投资最小、可靠性提升成本效益最高、配电网损耗最小。而求解多目标优化问题的过程就是寻找Pareto最优解的过程。所谓的Pareto最优解也被称为非劣最优解。若x*是决策变量中的一点,当且仅当在搜索空间的可行域内不存在x使得fn(x)≤fn(x*)(n=1,2,…,N)成立时,称f(x*)为非劣最优解。对于多目标优化问题,当且仅当在搜索空间中的任意,都有,则称为全局最优解。由所有非优劣最优解组成的集合称为多目标优化的最优解集。将可靠性规划中的单个优化目标的取值作为坐标系的纵、横轴,按照各个单目标的取值描点连线,所得到的就是Pareto优化曲线。
多目标优化问题的Pareto最优解(Pareto Optimal Solutions)的定义为:在控制变量u和状态变量x的取值范围内,对于变量组(u*,x*),当且仅当不存在其它的变量组(u,x),在不违背约束的条件下同时满足[5-7]:
fi(u,x)≤fi(u*,x*)
(1)
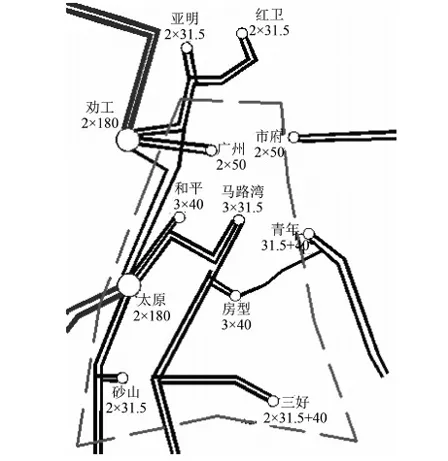
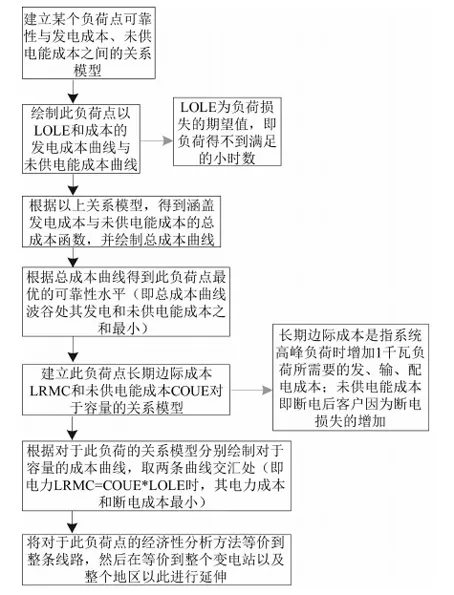
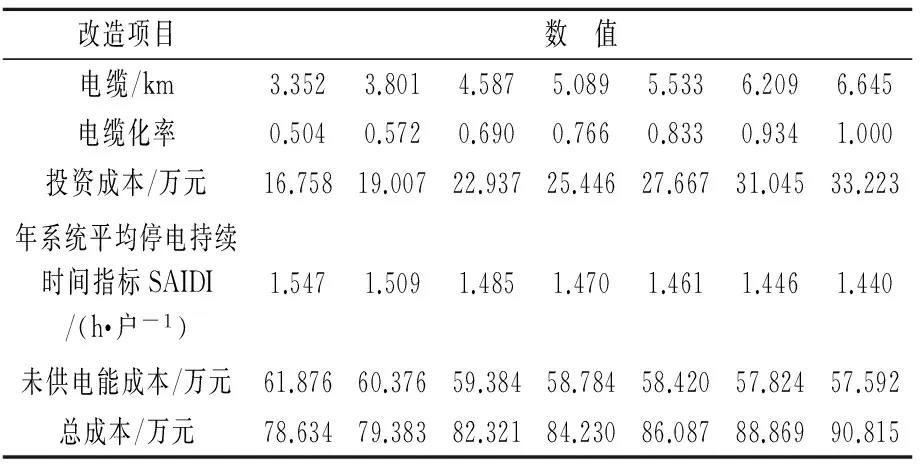
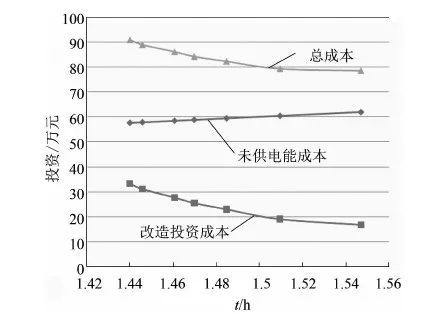
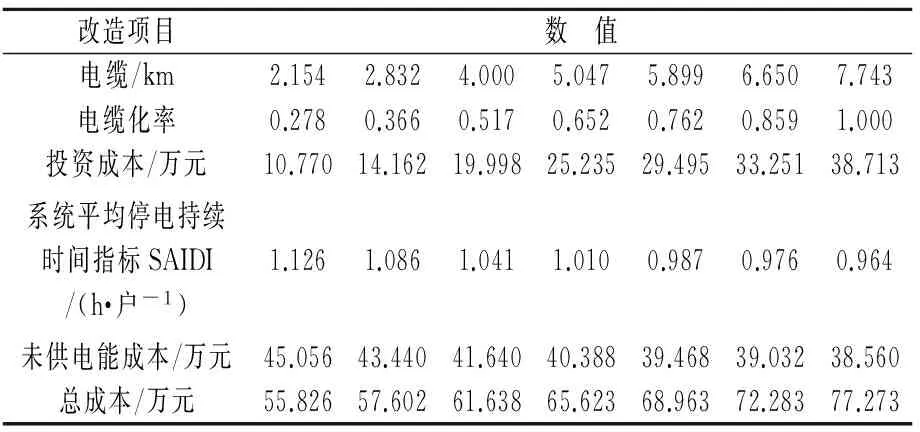
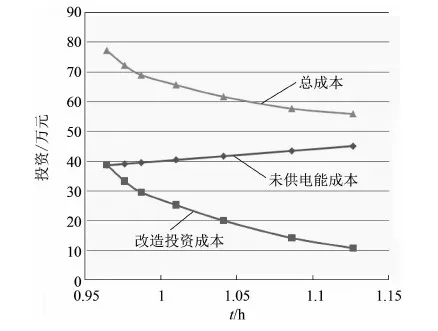
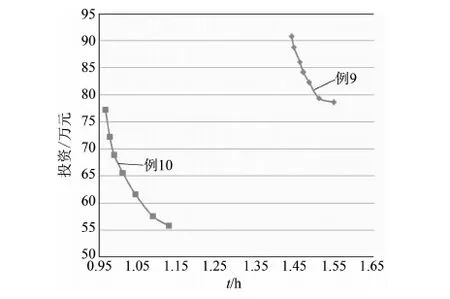
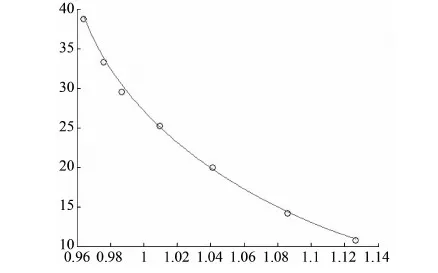
至少有一个目标函数使fi(u,x) 3.1 现状电网分析 选取某市一典型供电区为示例,市区面积40 km2,属于A类供电区。供电区内共有7个高压变电站,包含一个220 kV变电站,6个66 kV变电站,共有170条10 kV馈线(见图1)。 图1 某市区66 kV及以上电网地理接线示意图 3.2 基于边际成本与未供电能成本的Pareto曲线绘制 为解决并找出公司整体对应供电可靠性最优的投资(及效益最大化),故通过利用帕累托曲线特点与算法流程应用到实际案例,实现公司整体最优投资的选取。Pareto曲线绘制思路流程图如图2所示。 图2 Pareto曲线绘制思路流程图 3.2.1 建立具体实例 该市区配电网可靠性较高,属于A类供电区。根据线路的实际情况,选择线路电缆化率为电网可靠性影响因素,实际计算分析电缆更换项目的投资效益。 在市区配电网中,选取变电站两条馈线为例1和例2。通过逐步更换电缆线路的改造方案,研究随着改造项目的实施,所得的效益和投资成本的关系。线路1全长为6.645 km,其中电缆线路3.352 km,电缆化率为50.4%。对线路1进行改造,将架空线逐步更换为电缆线路,计算统计所得效益和总成本。系统停电时间由1.547 h减少到1.440 h,总投资为12.181万元。例1改造项目投资成本和效益如表1所示。线路1的总成本与效益的关系曲线如图3所示。 表1 例1改造项目投资成本和效益 图3 线路1的总成本与效益的关系曲线 例2是选取青年变电站一条馈线。线路10全长为7.743 km,其中电缆线路2.154 km,电缆化率为27.8%。对线路2进行改造,将架空线逐步更换为电缆线路,计算统计所得效益和总成本。系统停电时间由1.126 h减少到0.964 h,总投资为21.447万元。例2改造项目投资成本和效益如表2所示。线路2的总成本与效益的关系曲线如图4所示。线路1和2的总成本与效益的关系曲线如图5所示。 表2 例2改造项目投资成本和效益 图4 线路2的总成本与效益的关系曲线 图5 线路1和2的总成本与效益的关系曲线 3.2.2 拟合曲线函数 根据实际计算结果,线路的项目改造效益和总投资成本的曲线近似于指数函数曲线,通过Matlabe软件和实际计算结果模拟指数函数。Matlabe软件拟合曲线图(线路2)如图6所示。 其中总投资成本包括改造投资成本和用户未供电能成本。设定指数函数的公式为: y=a+be-cx (2) 得出指数函数系数: a=20.685 3 b=47.163 3 c=2.322 2 y1=20.685 3+47.163 3e2.322 2x (3) 图6 Matlabe软件拟合曲线图(线路2) 未供电能成本曲线是线性曲线,是二元一次函数,表达式为y=a+bx。其计算公式为: 未供电能成本=系统停电时间×停电损失估算值×系统用户负荷 线路2的系统用户负荷为4 000 kW,停电损失估算值取100元/kWh,则有: a=0 b=40 y2=40x y3=20.685 3+47.163 3e2.322 2x+40x (4) 式中y1——项目改造投资金额;y2——用户未供电能成本;y3——总投资。 在根据Pareto曲线得出的公司最优投资成本的基础上,结合可靠性边际成本矩阵思想,计算在最优投资成本基础上的不同改造或规划措施对各个层级之间或其层级本身的可靠性成本提升效果(层级代表输电层、变电站层、配电网、低压供电层等)。 总体思路:建立实例,针对于不同层级的改造规划措施计算对某一层级供电可靠性的边际成本,然后得出总体的边际成本矩阵,矩阵中各边际成本值的大小即为项目的优选排序。 电力系统可靠性与费用之间存在非线性关系。高可靠性要花钱,更高的可靠性则要花更多的钱。这不仅出于技术原因,更出于实际的考虑:高效的规划是首先选择可靠性边际成本最低的项目,但这意味着余下项目的可靠性边际成本会更高。本文介绍的基于成本效益的可靠性改进方法是一种比较有效的方法。该方法不仅简单实用,而且全面可信;它只需要电力企业现成的数据和技术,不需依赖大量代价昂贵的“数据挖掘”,不需搜寻支出和运行(可靠性)的历史记录,也不要求进行本项研究的规划人员具备特殊的技巧,更不要求使用高级可靠性分析研究。 对基于可靠性的规划中可靠性与费用的关系问题,有以下几点重要建议: (1) 基于投资(金钱)回报(可靠性)的方案收益/成本边际(或增量)分析和优先级分析,是保证优化使用资金、时间和资源的最好方式。 (2) 系统论的方法具有全面的视角。无论何处何时,都要寻求进行“议价”的空间。系统单个层级的可靠性与客户层的可靠性无关,只与费用有关,客户可靠性处于电力系统链条的终端。 (3) 所有层级内和层级间的可靠性改进措施都应该考虑,以确保最有效地使用系统能力。为了解决规划问题,所有这些措施都用层级内/层级间的边际成本矩阵表达。 (4) 层级内可靠性支持,所考虑的是电力系统某一层级内的固有可靠性及自身设备承担事故的能力;层级间可靠性支持,所考虑的是一个层级支持或解决另一层级的停运或事故的能力。层级内/层级间可靠性边际成本矩阵,提供了在给定情况下确定实施可靠性最“便宜”层级的方法,从而为可靠性规划提供了一种有用的策略性工具。 [1] 张 宁,马孝义,陈帝伊,等.输配电网规划优化模型的研究进展[J].水利与建筑工程学报,2011,9(1):10-16. ZHANG Ning, MA Xiao-yi, CHEN Di-yi, et al. Research progress on optimal planning models for power transmission and distribution networks[J].Journal of Water Resources and Architectural Engineering, 2011, 9(1): 10-16. [2]范明天,苏傲雪.基于可靠性的配电网规划思路和方法讲座二基于可靠性规划的项目评估方法[J].供用电,2011,28(2):12-17. FAN Ming-tian, SU Ao-xue. Ideas and methods of power distribution network planning based on reliability lecture 2 the project assessing method based on reliability planning[J].Distribution & Utilization, 2011, 28(2): 12-17. [3]江知瀚,陈金富.计及不确定性和多投资主体需求指标的分布式电源优化配置方法研究[J].中国电机工程学报,2013,33(31):34-42. JIANG Zhi-han, CHEN Jin-fu. Optimal distributed generator allocation method considering uncertainties and requirements of different investment entities[J].Proceedings of the CSEE, 2013, 33(31): 34-42. [4]黄嘉健,王昌照,郑文杰,等.基于状态监测的配电网可靠性检修选择模型[J].电网技术,2015,39(1):164-168. HUANG Jia-jian, WANG Chang-zhao, ZHENG Wen-jie, et al. Reliability-centered maintenance selection model for distribution network based on condition monitoring[J].Power System Technology, 2015, 39(1): 164-168. [5]王成山,孙充勃,李 鹏.主动配电网优化技术研究现状及展望[J].电力建设,2015,01:8-15. [6]屈高强,李 荣,董晓晶,等.基于随机机会约束规划的有源配电网多目标规划[J].电力建设,2015,36(11):10-16. QU Gao-qiang, LI Rong, DONG Xiao-jing, et al. Multiple-objective planning of active power distribution network base0d on random chance constrained programming[J].Electric Power Construction, 2015, 36(11): 10-16. [7]刘 芳,李 冰,张 帆.计及配电网经济性与可靠性的电池储能系统优化配置[J].电力建设,2015,36(12):76-83. LIU Fang, LI Bing, ZHANG Fan. Battery energy storage system optimal allocation considering economy and reliability of distribution network[J].Electric Power Construction, 2015, 36(12): 76-83. (本文编辑:赵艳粉) Pareto Optimal Multi-Objective Programming in Power Distribution System LIU Yi-tao, ZHANG Nan, JIANG Tao, WANG Zheng (State Grid Liaoning Electric Power Co., Ltd., Shenyang 110006, China) Based on the pareto optimality of the power supply reliability curve of ideas, in combination with the characteristics of the pareto curve and according to the algorithm process, the optimal investment is selected for the whole company. This study aims to solve and find out the scheme for optimal investment and maximum profit corresponding to power supply reliability, and present feasible suggestions to deal with the relationship between reliability and cost on reliability planning. power distribution system; pareto optimal; optimal investment; reliability programming 10.11973/dlyny201606001 刘一涛(1971),男,硕士,高级工程师,从事电网调度、规划管理工作。 TM715 A 2095-1256(2016)06-0669-04 2016-08-153 算例应用分析
4 基于可靠性边际成本矩阵实现项目优选排序
5 结语

