有限元方法应用于一维屏蔽计算的研究
赵京昌,张斌,陈义学
(华北电力大学核科学与工程学院,北京 102206)
有限元方法应用于一维屏蔽计算的研究
赵京昌,张斌,陈义学
(华北电力大学核科学与工程学院,北京102206)
摘要:应用确定论方法,对一维平板及一维球的屏蔽计算进行了研究,采用离散SN-有限元方法开发出一维稳态中子输运计算程序DONTRAN1D。在处理模型边界条件时,提出设置虚拟点的方法。对负通量除采用置零修正外,还使用输运方程进行中子平衡计算。最后应用该程序进行算例验证,并与国际上成熟的程序进行比较分析,求解精度能得到很好的保证。同时,程序中还保留了大量功能模块接口,便于以后继续开发之用。
关键词:一维;屏蔽计算;有限元;中子输运
0 引言
随着我国核电事业的迅速发展,公众对核电安全性要求的呼声越来越高。合理有效的屏蔽设计可以确保辐射剂量安全,也能保证核动力装置的正常运行。屏蔽计算的主要任务是给出辐射粒子的空间精细分布,因此,在数值求解中对空间变量的离散处理至关重要。20世纪50年代,有限元方法开始在工程问题的数值求解中广泛应用。20世纪70年代初,有限元方法开始应用在反应堆数值计算领域[1],利用有限元方法求解一维单能稳态中子输运问题,显示出了这一方法的巨大优越性。本文首先简要介绍粒子输运的概念,然后给出基于有限元方法的一维平板和一维球的屏蔽计算迭代解法。在处理反射边界处的通量时,在几何模型外部设置了虚拟点,以适应输运方程的求解。对负通量除采用置零修正外,还使用输运方程进行中子平衡计算。通过算例,将自主开发的计算程序DONTRAN1D与国际上先进的程序进行比较。
1 中子输运方程
1.1输运方程的建立
研究中子输运过程应用的一条基本原理是“中子数守恒”,即在一定体积内,中子总数对时间的变化率应该等于该体积内中子的产生率减去该体积内中子的泄漏率和移出率。
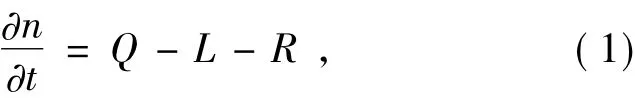
式中: n为中子总数; t为时间; Q为中子产生率; L为中子泄漏率; R为中子移出率。
本文研究屏蔽计算方法,只讨论平衡状态,也就是中子数变化率为零的情形。此时,输运平衡方程可写为
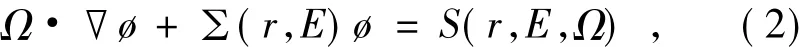
方程中的3项分别为泄漏项、移出项和产生项。产生项中的中子来源有散射源、裂变源和独立的外中子源。
1.2定解条件
上文导出的中子输运方程是一个微分积分方程,它只表示中子守恒规律的数学形式。为了封闭这一物理过程的数学描述,还必须确定初始条件和边界条件,才能使方程的解有定值。从中子角通量的物理意义知道,在方程所适用的区域内,它应当是连续的、有限非负实数。
边界条件比较复杂,它依赖于所研究问题的性质。解中子输运方程常遇到的边界条件如下。
(1)两种不同介质的分界面。若两种介质直接接触,其间没有源和其他物质插入,那么根据连续性条件,在分界面上应满足=(r,E,Ω)在交界面上沿Ω方向是r的连续函数。若交界面中插入第3种介质或源,就必须考虑中子穿过这层介质的效应,这时就必须对上述边界条件加以修正。
(2)自由表面。自由表面指粒子只能从系统中逃出,而不能再进入这一系统。假定中子输运过程发生的区域由凸的且分块光滑的曲面围成,中子自表面逸出后就不可能再返回到域中来。这样,与真空交界的凸表面就是自由表面。
(3)反射边界。在反射边界上,某个方向的入射中子角通量密度等于与之对应的反射方向的出射中子通量密度。反射边界条件往往用来表示解的对称性质,例如,在系统的对称点、对称轴或对称面上经常使用反射边界条件来减少计算量。
(4)反照边界。反照边界与反射边界类似,但入射角通量密度或中子流与出射角通量密度或中子流不相等,两者的比值为一个小于1的常数α,通常将α称为反照系数。
2 有限元方法应用于一维屏蔽计算
输运方程中,中子通量密度是由空间位置、能量和角度共同约束的。进行数值计算时,需要对这些变量做相应的离散化处理。
2.1角度及能量变量的近似
对角度变量的处理采用传统的离散纵标SN方法,但仅限于中子通量密度,源项仍设置为各向同性源。离散纵标SN方法就是利用特别选定的一组方向余弦值{μm} (m = 1,2,…,N)把输运方程离散化。用一组离散的角度坐标变量Ωm(m = 1,2,…,N)来代替连续的坐标变量Ω,在这些特定的方向上对输运方程进行数值求解,再用数值求积公式近似表示函数对Ω的积分[2]。对中子角通量密度的积分可表示为

式中: N为总的离散方向数;ωm为每个方向的求积权重。为表示方便,这里略去了能量变量下标。
一维平板和一维球的输运方程经角度离散后变为

本文对能量变量的近似处理采用的是数值计算中最常用的分群方法。角通量的能量关联问题,与坐标系没有多大关系,因此,为不失一般性,以一维平板输运方程为例,它的多群形式可写为

式中:下标g为能群编号; Qs和Qf分别为本能群的总散射源和总裂变源。
2.2空间变量的近似
在这一部分,本文不再使用传统的菱形差分,而是将线性间断有限元方法用于空间变量的离散。采用这种非连续的方法,可得到非常精确和稳定的差分组合。
每个空间网格都有两个边界通量值,但两个相邻网格有一条公共边界,因此每条公共边界有两个边界通量值,将这两个通量值看作边界两旁接近边界处的通量值。这两个值可能不等,即角通量在网格内部连续,但在网格边界是间断的[3]。
空间变量离散后,对输运方程的求解转变为对一系列线性方程组的求解。以夹角余弦为正的情形为例,对于平板的第k个网格和第m个离散方向有

式中:Δx为网格长度;上标b表示该变量来自相邻网格。
2.3负通量修正
在网格边界处求得的角通量可能为负,尤其是在无源粗网格中。由于负中子通量没有物理意义,并且它还会在很大程度上影响计算的稳定与精确性,应予以修正。
本文在置零修正法的基础上又应用了一个加强条件。对一个给定空间网格的求解,首先使用标准的线性间断有限元方法进行计算。当负通量出现后,立即将其置零,网格内其余点的通量重新计算。置零后,网格内有一个点的通量变为已知值,这时只需求解一个方程便能确定另一点唯一的通量值。因为所乘的权函数值为1,所以形式上就是离散化了的输运方程。
3 程序开发与验证
3.1功能及特点
DONTRAN是华北电力大学核反应堆物理与屏蔽研究所正在开发的大型三维输运屏蔽计算程序,整体采用离散纵标SN方法,DONTRAN1D是对其中的一维问题采用更有优势的有限元方法求解的程序。DONTRAN1D采用确定论方法对中子输运方程进行数值迭代求解。方向变量的离散使用离散纵标法,空间变量离散使用有限元方法,能量变量则用分群近似处理。采用外-内迭代方法,在所有几何、能群、方向上对离散方程组进行迭代求解,获得中子通量密度的分布。本程序可对一维平板以及一维球模型的多群中子输运方程求解,主要用于核系统辐射屏蔽计算,也可用于核装置的设计分析。
3.2测试算例
本文针对DONTRAN1D的功能设计了多个算例。屏蔽中最常使用的材料是不锈钢,设计算例时将其简化,只取56Fe一种核素,核子密度采用SS316不锈钢中铁的核子密度,温度为常温。使用TRANSX程序计算出反应截面数据。求积组统一取S16高斯-勒让德求积组,内迭代收敛精度为0.0001,网格均匀划分。验证单群计算功能的算例有4个,分别测试不同的几何形状和固定源分布,计算参数见表1。
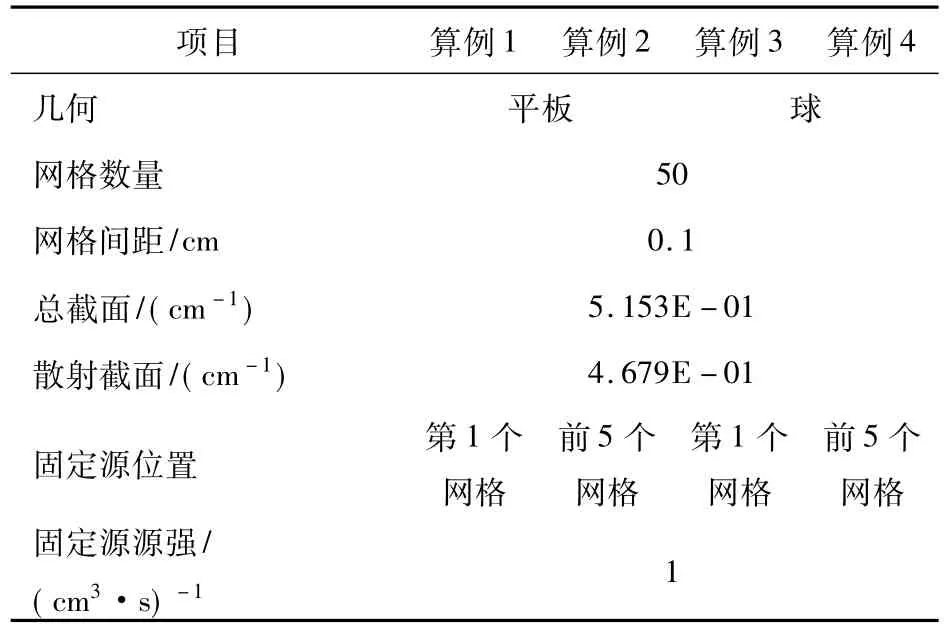
表1 单群计算参数
多群中子的测试只计算三群中子的情况,因为多于三群中子的迭代算法与三群中子的算法是相同的。由于单群测试时已经验证过,所以也不再考虑固定源分布的差异。多群计算参数见表2。
3.3计算结果与分析
将DONTRAN1D的计算结果与ANISN的计算结果作对比分析。ANISN是美国橡树岭国家实验室研发的一维输运程序,是公认的精度高和稳定性好的计算程序。对角度变量的离散同样使用离散纵标法,而对空间变量的离散则采用传统的有限差分法。
图1~图4为4个单群中子算例的计算结果,从图中曲线可见,DONTRAN1D与ANISN的计算结果吻合度极高。4个算例所有网格点通量值的最大相对误差分别为-0.33%,-0.15%,-9.34%和2.68%,算例3和算例4的最大相对误差分别出现在第3个网格和第1个网格,在离源较远的区域,相对误差均下降到0.10%以下。
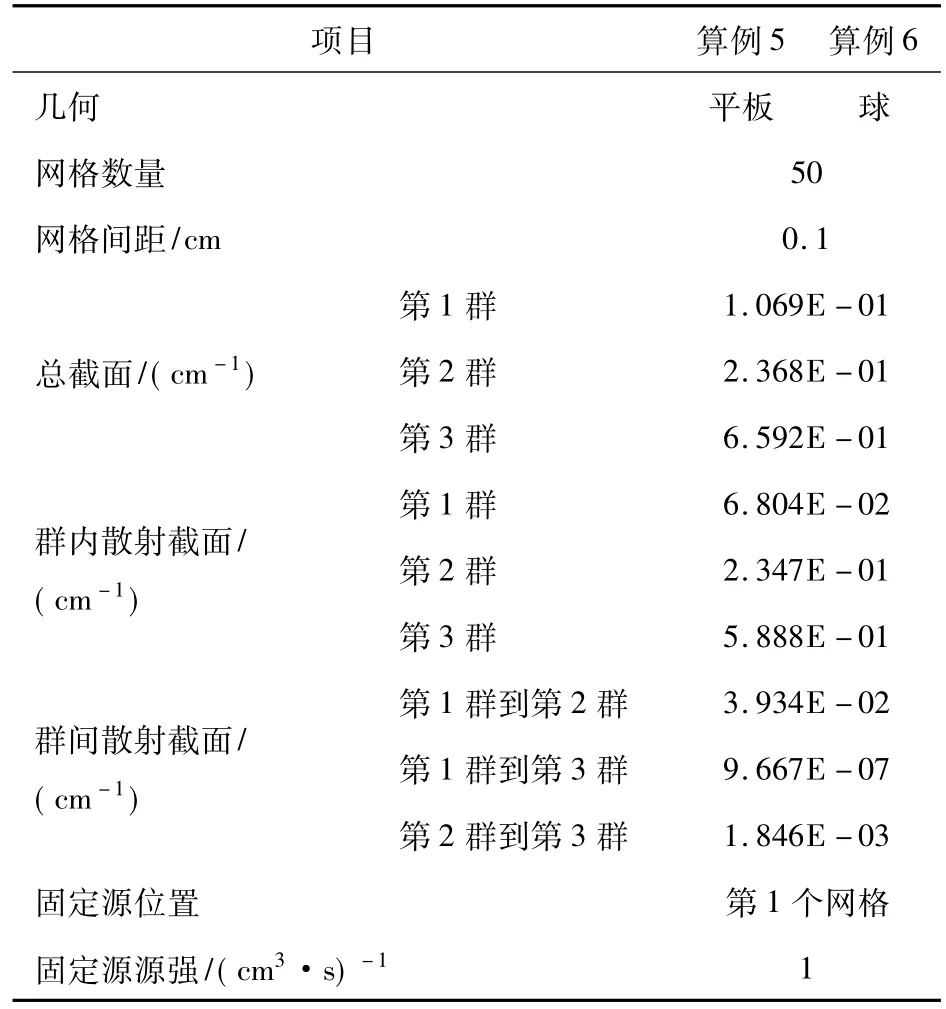
表2 多群计算参数

图1 算例1计算结果
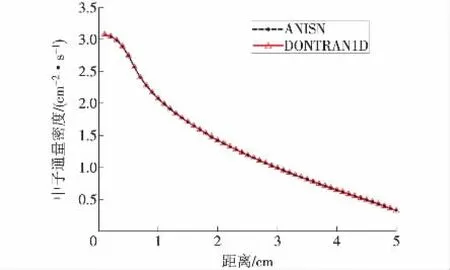
图2 算例2计算结果

图3 算例3计算结果

图4 算例4计算结果
经分析,产生上述问题的原因在于,DONTRAN1D处理反射边界条件时,在几何模型外部设置了一个等值虚拟点,然后套用输运方程求解。这里只使用了输运方程组中的一个方程而非整个方程组,权函数的作用没有完全体现出来,由此求出的通量值对后续网格的计算势必产生影响。
三群中子算例的计算结果如图5、图6所示,从图中曲线可以看出,两个程序的计算结果吻合度也是非常高的。

图5 算例5计算结果

图6 算例6计算结果
算例5(几何为平板)的最大相对误差出现在第3群第2个网格,为-0.43%;算例6(几何为球)的最大相对误差出现在第3群第3个网格,为-9.70%。误差出现的原因,除上述提到的虚拟点外,还有群间散射源的影响。在计算第1群散射到第3群以及第2群散射到第3群的散射源时,要用到第1群和第2群的中子通量密度,所以前两群计算结果的误差将会累积到第3群中,使得第3群的相对误差最大。
4 结束语
本文对有限元方法应用于一维屏蔽问题的数值计算进行了初步研究,介绍了自主开发的计算程序DONTRAN1D,并通过算例与国际上的先进程序进行对比,计算精度总体上令人满意。在处理模型边界条件时,提出设置虚拟点的方法。对负通量的处理除采用置零修正外,还再次利用输运方程进行中子平衡计算,效果十分明显。
参考文献:
[1]MACHORRO E.Discontinuous Galerkin finite element method applied to the 1-D spherical neutron transport equation[J].Journal of computational physics,2007,223 (1) : 67-81.
[2]HILL T R.ONETRAN: a discrete ordinates finite element code for the solution of the one-dimensional multigroup transport equation[R].New Mexico: Los Alamos Scientific Laboratory,1975.
[3]杜书华.输运问题的计算机模拟[M].长沙:湖南科学技术出版社,1989.
[4]ADAMS M L.Discontinuous finite-element transport solutions in the thick diffusion limit in Cartesian geometry[R].Califor-nia: Lawrence Livermore National Laboratory,1991.
[5]KUZMIN D.A guide to numerical methods for transport equa-tions[D].Freistaat Bayern: Friedrich-Alexander-Universität Erlangen-Nürnberg,2010.
(本文责编:刘芳)
赵京昌(1990—),男,山东潍坊人,在读硕士研究生,从事反应堆输运屏蔽方面的研究工作(E-mail: zhaojczhaojc@ 163.com)。
作者简介:
基金项目:国家自然科学基金(11575061)
收稿日期:2015-10-15;修回日期:2015-12-20
中图分类号:TL 328
文献标志码:A
文章编号:1674-1951(2016)01-0001-04

