向数学的纵深处迈进——《面积的变化》教学

杨宏权 周正琴

【教学内容】

苏教版六年级下册第48～49页。

【教学过程】

板块一：从“一次争论”说起……

出示：3cm的线段和比例尺 1∶1000。

让学生叙述图中信息，回忆什么是比例尺（板书：长度比），并让学生算出图上3厘米的实际距离。

出示：乒乓球活动室的平面图。

引出“求球馆的实际面积到底有多大？”健健和康康发生的争论。

健健的想法：

2×3=6（平方厘米）

6×1000=6000（平方厘米）

6000平方厘米=0.6平方米

康康的想法：

2×3=6（平方厘米）

6×1000000=6000000（平方厘米）

6000000平方厘米=600平方米

引出猜想：面积比与长度比，会有什么样的关系呢？通过“你打算采用什么样的方法来研究这个问题”，激发学生思考，通过生生之间的交流，让学生初步认识可以通过画图形、放大、算一算的方法进行判断。

出示智慧心语：解决问题前，通常需要根据问题的特点设计解决问题的方案。

板块二：由长度比到面积比。

1.举例，初步感知。

以长方形为例，任意画一个长方形。出示1cm×3cm的长方形，再把它放大并分别出示三个长方形：3cm×3cm、1cm×9cm、3cm×9cm。让学生选一选，哪个是原长方形放大后的图形？为什么？按什么比放大的？

接着让学生算一算大长方形与小长方形的面积分别是多少？面积比呢？最后得出：大长方形与小长方形的面积比是9∶1。

2.提升，归纳规律。

通过上面的举例，学生发现长度比是3∶1，而面积比却是9∶1，得出“长度比并不等于面积比”，从而引发学生进一步思考：面积比可能与长度比存在怎样的关系呢？再次引发学生猜想（面积比可能等于长度比的平方），并引导学生讨论：根据一个例子我们能说面积比就一定等于长度比的平方吗？（不能）从而得出：要想知道这一猜想是否具有普遍性，可以再举些例子进行验证。

出示：如果将小长方形按（ ）∶（ ）的比放大，放大后与放大前图形的面积比是（ ）∶（ ）。

学生自由选择，并独立完成。然后选择两种用不同比放大的作业进行展示，观察归纳。算出面积和面积比,指名讲解。从而得出：把一个长方形按n∶1的比放大，放大后与放大前长方形的面积比是n2∶1。

这时教师再次激疑：通过举例验证，我们发现这样的规律适合长方形，它是否也适用于其他平面图形呢？从而将学生的探索思维向其他平面图形延伸。

给出正方形、平行四边形、三角形和圆等。让学生选一种或几种以前学过的平面图形，再将它按一定的比放大，算一算、填一填，完成作业纸。反馈，指名上台讲解。逐个得出，这一规律同样适用于正方形、平行四边形、三角形和圆。总结得出规律：把一个平面图形按n∶1的比放大，放大后与放大前图形的面积比是n2∶1。

出示智慧心语：由特殊到一般，是验证猜想的重要环节。

3.溯源，解释规律。

教师引导：刚才我们得出的规律虽然已经通过实践的检验，但是一个结论的得出还需通过科学的论证。以长方形为例，出示平面图。

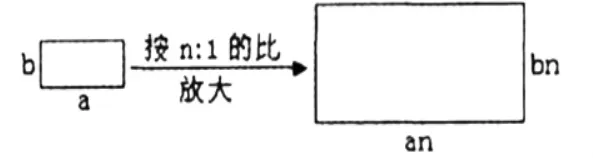
让学生通过计算说明：

小长方形的面积：a×b=ab

大长方形的面积：（an）×(bn)=abn2

最后，引导学生发现，通过积的变化规律，揭示其中的奥秘。

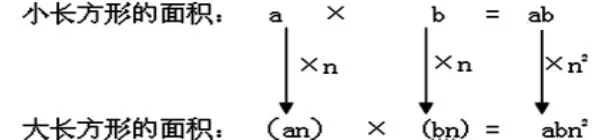
引导学生上下对比这两道算式，并用以前所学的知识来解释面积的变化规律。从而得出：一个因数扩大n倍，另一个因数也扩大n倍，积就扩大n2倍。

教师再次引导学生用积的变化规律来解释其他的平面图形长度比与面积比的关系。学生选择其中一个平面图形论证，先在作业纸上写一写，再说给同桌听一听。

出示智慧心语：追根溯源，就能找到规律的本质。

4.运用，丰富规律。

（1）解决乒乓球馆问题。出示前面的例题，让学生判断一下，谁计算正确？健健错在何处呢？再让学生用新学的知识计算乒乓球活动馆的实际面积。

2×3=6（平方厘米），6×10002=6000000（平方厘米），6000000平方厘米=600平方米。

（2）明明想给乒乓球活动馆布置一张长9米、宽6米的乒乓球奥运冠军的宣传画，如果按1∶30的比把宣传画缩小，缩小后这张宣传画的面积是多少?

9×6=54（平方米），54÷302=0.06（平方米）。

由此题引出：把一个平面图形按1∶n的比缩小，缩小后与缩小前图形的面积比是1∶n2。

5.回顾，积累经验。

回顾我们探究与发现的过程。我们先通过长方形个例，有了猜想，再通过举例子来检验，接着追根溯源论证了检验的结果，最终总结出了具有普遍性的结论。这样一步一步地使得出的结论越来越缜密与完备。这也是我们解决问题的一般流程。（课件演示回顾过程）

板块三：由 n2：1想到的……

牛顿有句名言：“没有大胆的猜想,就没有伟大的发明和发现。”教师再次激疑：根据长度比，如果给你大胆猜想的机会，你还会有哪些猜想呢？引导学生从面积，想到周长，再从平面图形想到立体图形。得出如下网络。

学生有了猜想后，可试着让学生验证一下。全班汇报、交流。

出示智慧心语：大胆猜想，严密验证，将会有更多的发现。

【课后思考】

思考1：整体性——从“一维教学”走向“三维思考”

教材中只介绍了从长度比向面积比的规律探索，其实细细思考，我们会发现，面积属于二维空间，由长度和宽度两个要素所组成的平面空间。而长度比则属于一维空间的范畴，这时我们又在思考，那我们能不能从长度比再引导学生向三维空间（立体图形）的体积比进行探索呢？教学实践告诉我们完全可行。为此，课始我们通过比例尺的复习（一维空间），然后过渡到面积比的探索（二维空间），再到最后的知识总结与提升阶段，激发学生对体积比产生新的猜想，这样的设计，我们从整体出发，在知识三维过渡中培养学生整体的眼光、整体的思维，感悟智慧的生长。

思考2：抽象性——从“是什么”走向“为什么”

教学中，教师往往通过计算平面图形的图上面积和实际面积的比来找到变化的规律，对规律背后的本质问题，为什么会这么变化却只字不提。这种研究仅仅局限在找现象规律，而数学是对现象的本质分析和探索，用数学方法研究这种现象正是我们要做的。面积属于二维空间，它的大小决定于长度和宽度两个变化量。这种变化与学生已学的积的变化规律是相通的。让学生探究现象背后的实质不仅能提高学习效率，还能举一反三，获得更大的思维发展。

思考3：探索性——从“知识传授”走向“素养形成”

通过“争论”引发学生的思考冲突，并通过长方形放大前后的比较诱发学生直觉猜想，并通过计算比较，佐证猜想的正确。此时，又告诉学生一个特例的正确，还不能完全证明猜想的正确性。这时又引导学生用不同平面图形的面积变化进行检验，从而进一步验证猜想的合理性。然后又通过激发学生通过旧知，即积的变化规律进一步论证猜想的科学性，最后通过总结得出缜密的规律。这样让学生经历“猜想——检验——论证——总结”的四个环节，循序渐进，步步深入，直觉思维与逻辑思维相互映照，这正是学生形成科学素养的过程。