《圆柱的体积》教学

白志阳 张 昕

【教学内容】

青岛版数学六年级下册第24～25页。

【教学过程】

一、复习导入，引发思考

（出示一张长方形纸）

师：你能想办法把它变成一个圆柱吗？

学生出现两种情况：

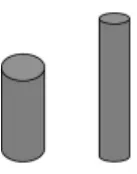
师：用同样一张长方形纸围成了两个不同的圆柱体，想一想这两个圆柱体有什么不同吗？

生：一个侧面比较高一点另一个底面比较大一点。

生：它们的底面直径和高都不相同。

师：同学们，这两个圆柱哪一个的体积会大一点呢？

（多数学生猜测体积相等）

师：到底怎样？这节课我们就来研究圆柱的体积。

二、运用迁移，回顾旧知，学习新知

1.回顾圆面积的推导过程。

师：大家看，这是一个圆柱，它的底面是一个圆形（课件出示），同学们，回想一下，我们是怎样推导出圆面积计算公式的？

生：把圆等分成若干份，拼成一个近似的长方形，面积不变，长方形的宽等于圆的半径，长等于圆周长的一半，因为长方形面积等于长乘宽，所以圆的面积等于底面周长的一半乘半径，S=πr2。

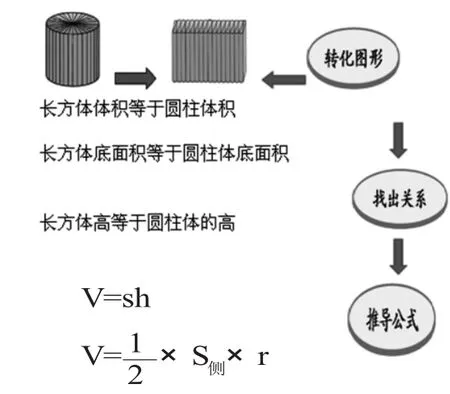
2.圆柱转化成长方体。

师：把圆转化成学过的长方形，也就是把未知的转化成已知的，可以求出面积，对于圆柱大家有没有什么想法？

生：如果把很多个圆重叠起来可以形成一个圆柱，圆分成若干等份拼成一个长方形，我认为圆柱也可以分成若干等份拼成一个长方体。

师：太棒了，非常善于动脑，思维灵活并且联系了前后之间的知识。

师：（课件演示）当这个圆垂直升高的时候就可以形成一个圆柱。把圆的底面分成若干的等份，沿圆柱的高切开，就分成了近似的三菱柱，怎样才能将圆柱转化成长方体呢？请同学们拿出自己的学具动手试一试。

师：把你拼的展示给大家看看。为什么圆柱拼成的是一个近似的长方体？

生：因为它的这条棱不是直的，它的底面是一个圆形拼成的。

师：怎样才能更像一个长方体？

生：等分的份数多一些。

课件演示，分成32等份、64等份……继续分下去，当分的份数越多，小扇形的弧度就越小，拼成的图形就越接近长方体，当平均分的份数我们用肉眼看不出来的时候，这个小弧形实际就是一个点，长方体的一条长就近似于一条直线，可以拼成一个长方体。

三、梳理推导方法，自主探究圆柱体的计算公式

1.梳理圆面积的推导方法。

师：刚才我们把圆柱体转化成了长方体，回想一下，咱们在探究圆面积计算公式的时候，经历了一个怎样的过程呢？

生：先是把圆转化成学过的长方形，然后找出它们的关系，最后推导出公式。

（课件演示略）

2.自主探究圆柱体积计算公式。

师：刚才我们回顾了圆面积计算公式的推导过程，你能用这样的方法探究圆柱体积的计算公式吗？你想经历哪几步？第一步转化图形完成了，剩下的需要小组合作去探究了，小组长借助探究卡记录你们探究的过程。

师：下面老师来当学生，你们当老师，把你们小组的探究过程展示给同学们。

组1：我们组觉得这个长方体的上底面就等于圆柱体的上底面，长方体的高等于圆柱体的高，因为长方体体积等于圆柱体体积，又因为长方体体积等于底面积×高，所以圆柱体体积也等于底面积×高。用字母表示是：v=sh。

组2：我们组发现长方体的长等于圆柱底面周长的一半，宽等于圆的半径，高等于圆柱体的高，因为长方体体积等于圆柱体体积，又因为长方体体积等于长×宽×高，所以圆柱体体积等于底面周长的一半×半径×高。用字母表示是：v=πr2h。

组3：我们组是这样观察的，发现长方体的底面积等于圆柱侧面积的一半，高等于圆柱体的高，因为长方体体积等于圆柱体体积，又因为长方体体积等于底面积×高，所以圆柱体体积等于侧面积的一半×高。用字母表示是：

3.梳理圆柱体积计算公式的推导方法。

师：同学们很了不起，发现了圆柱体积的计算公式，并且发现把长方体进行不同的摆放，可以得出不同的公式。

回想一下我们在研究圆柱体积计算公式的时候，我们经历了一个怎样的过程？

生：我们先把圆柱体转化成长方体，再找出它们的关系，最后推导出公式。

4.沟通联系。

师：回想圆面积计算公式和圆柱体积计算公式的推导过程有什么联系和区别？

三、自主练习，巩固应用

1.已知圆柱体底面积是26平方米，高是10米，圆柱体的体积是多少？

2.一个长20厘米，宽10厘米的水槽内装有水，水深8厘米，把这些水倒入底面面积是80平方厘米的圆柱形容器中，水深多少厘米？

3.一个圆柱的侧面积是10平方米，半径是5米，这个圆柱的体积是多少立方米？

4.在开始我们用同样一张纸围成了两个不同的圆柱体，你能用刚刚学到的知识解释哪个体积大吗？