基于HMM和切削振动的硬车削工件表面粗糙度精度等级监测

何　康，贾民平，唐永刚，李恒征

1.宿州学院煤矿机械与电子工程研究中心，安徽宿州，234000；

2.东南大学机械工程学院，江苏南京，210089



基于HMM和切削振动的硬车削工件表面粗糙度精度等级监测

何康1，贾民平2，唐永刚1，李恒征1

1.宿州学院煤矿机械与电子工程研究中心，安徽宿州，234000；

2.东南大学机械工程学院，江苏南京，210089

摘要：为了对硬车削工件表面粗糙度(Ra)进行有效监测，在分析切削振动对工件表面形貌影响的基础上，提取了基于SSA的多通道融合特征；针对传统的隐马尔科夫模型(HMM)概率比对法的不足，提出了一种χ比对法用于HMM工件表面粗糙度精度监测。实验分析表明，采用χ比对法比采用概率比对法能够明显提高HMM的工件表面粗糙度精度等级识别率。相对于连续隐马尔科夫模型(MoG_HMM)(识别率83.3%), 离散隐马尔科夫模型(DHMM)具有较大的优势识别率(94.4%)，其能够完全满足在线的工件表面粗糙度精度等级监测要求。

关键词：工件表面粗糙度；隐马尔科夫模型；振动信号；硬车削

1问题的提出

硬车削作为一种潜在的替代传统磨削的高效加工方法，其工件表面粗糙度(Ra)常被用作评定工件表面质量的重要指标，但是，影响工件表面粗糙度形成的众多不可控因子增加了其在线监测的难度[1-2]。Benardos等[3]全面论述了当前所采用的工件表面粗糙度监测方法，指出基于人工智能所构建的监测模型具有较高的精度和实用性，建议考虑用尽可能多的状态信号(设备本身及其加工过程的状态信号)作为模型输入，但是文献并未指明哪种状态信号对工件表面粗糙度具有显著影响。Zhong等[4]指出,人工神经网络(ANN)的预测精度受到其参数设置的影响,并且到目前为止仍然没有精确解。

在当前所采用的监测信号中，切削力和切削振动被公认为具有实际意义[2]，与需要改动机床才能安装昂贵的测力计进行监测相比，振动监测简单易行，其在表面质量监测中扮演着重要角色[1,5]。在单点金刚石车削中，Wang等[5]考虑了工件对刀尖的冲击以及过程阻尼的影响，构建了一个单摆冲击模型来关联特征波峰和刀尖振动之间的联系。基于主切削方向振动信号的PSD分析，定义了一个CPR系数用于监测工件表面质量变化。Salgado等[1]的研究也表明，采用切削振动作为监测信号具有较好的经济性。除此之外，工件材料特性(如工件硬度)对工件表面粗糙度监测精度的影响长期被忽略了[6]，Mohamed和Hamdi等[7-8]通过方差分析表明，工件硬度对于工件表面粗糙度具有显著影响。但是，在当前文献中，缺乏基于多材料和工件硬度条件下的工件表面粗糙度监测方法。另外，基于单一方向振动信号的工件表粗糙度监测取得了很有意义的进展[1]，但是对于多通道融合特征的提取鲜有论及；并且较多文献都致力于单个样本的精度分析[6-8]。根据国标GB/T1031-2009，工件表面粗糙度的精度等级也是评判工件表面光洁度的重要标准，为此，基于切削振动信号，以SSA提取的多通道融合特征为输入，本文将改进的HMM用于工件表面粗糙度精度监测。

2特征提取

车削时刀尖在空间具有三个方向的振动位移，Wang等考虑了刀尖在y和z方向的振动位移对工件表面形貌的影响[5]。在实际切削过程中，刀尖沿进给x方向的振动位移实质上改变了相邻的两个刀尖圆弧半径轨迹在工件表面复映的交点，如图1所示。

由图1可以看出，p点表示不考虑进给方向振动位移时刀尖圆弧轨迹的交点，其中线为oo′,当考虑到由于刀尖沿进给方向振动时，刀尖产生位移ε，从而使交点p移到位置p′,如图中虚线所示，交点的改变使h0+/h0-的比值变为h1+/h1-，从而使中线变为o1o′1，并由此改变了工件表面粗糙度值的大小。为此，刀尖沿三个方向的振动对工件表面粗糙度均有直接的影响，提取三个方向的振动融合特征用于工件表面粗糙度监测是更加直接合理的方法。

图1　进给方向振动位移对工件表面形貌的影响

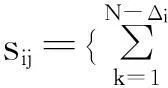
(1)

式中，I表示传感器的方向特性，r用来标识参予计算的初等矩阵，Lc={l∈Z+|1≤l≤L}。

3工件表面粗糙度精度识别模型

根据国标GB/T1031-2009评定的粗糙度轮廓(R轮廓)中的算术平均偏差Ra的精度等级，可以将工件表面粗糙度的精度等级监测问题通过HMM转化为一个模式分类问题。

(2)

(3)

对于DHMM:

(4)

对于MoG_HMM:

(5)

其中，

通常情况下{πi,aij}的初始化对HMM训练结果影响不大[9]，可随机或均匀选取，但是参数{bj(ot)}需要采用较为可靠的初始化方法。首先将模型随机初始化，然后采用Viterbi算法确定观测序列的最佳状态序列,估计参数{bj(ot)}。有限个工件质量精度组成隐状态集合Q，所提取的监测特征Pe组成观测序列集合O[11]。通常情况下都是比较概率大小，即用概率比对来判别结果，但是，由于振动信号的非平稳特性，要达到较高的识别率是比较困难的，为此，本文提出了一种χ比对法来取代传统意义上的概率比对法。

定义：设测试序列为O={O1,O2,…,Ok,…,OK},其中Ok={ok1,ok2,…,oki,…,okm}是第k个观测值序列样本, oki是它的第i个变长度观测向量，其长度为ki。设训练的模型为λχ,Sj,其表示第χ个精度等级的第Sj个状态，则Ok被判为状态Sj(1≤j≤N)的次数为：Njk=∑iargmax{logP(oki,Q|λχ,Sj)},1≤i≤m,则χ定义为：

(6)

基于HMM的工件表面粗糙度精度识别策略主要包括离线训练和在线监测两个步骤：离线训练主要为每种精度等级寻求近似最优参数{πi,aij,bj(ot)}；而在线监测主要是确定未知观测序列在各个模型参数下的对数释然概率(χ)。整个监测的基本流程如图2所示。

图2　基于HMM的Ra精度等级监测流程图

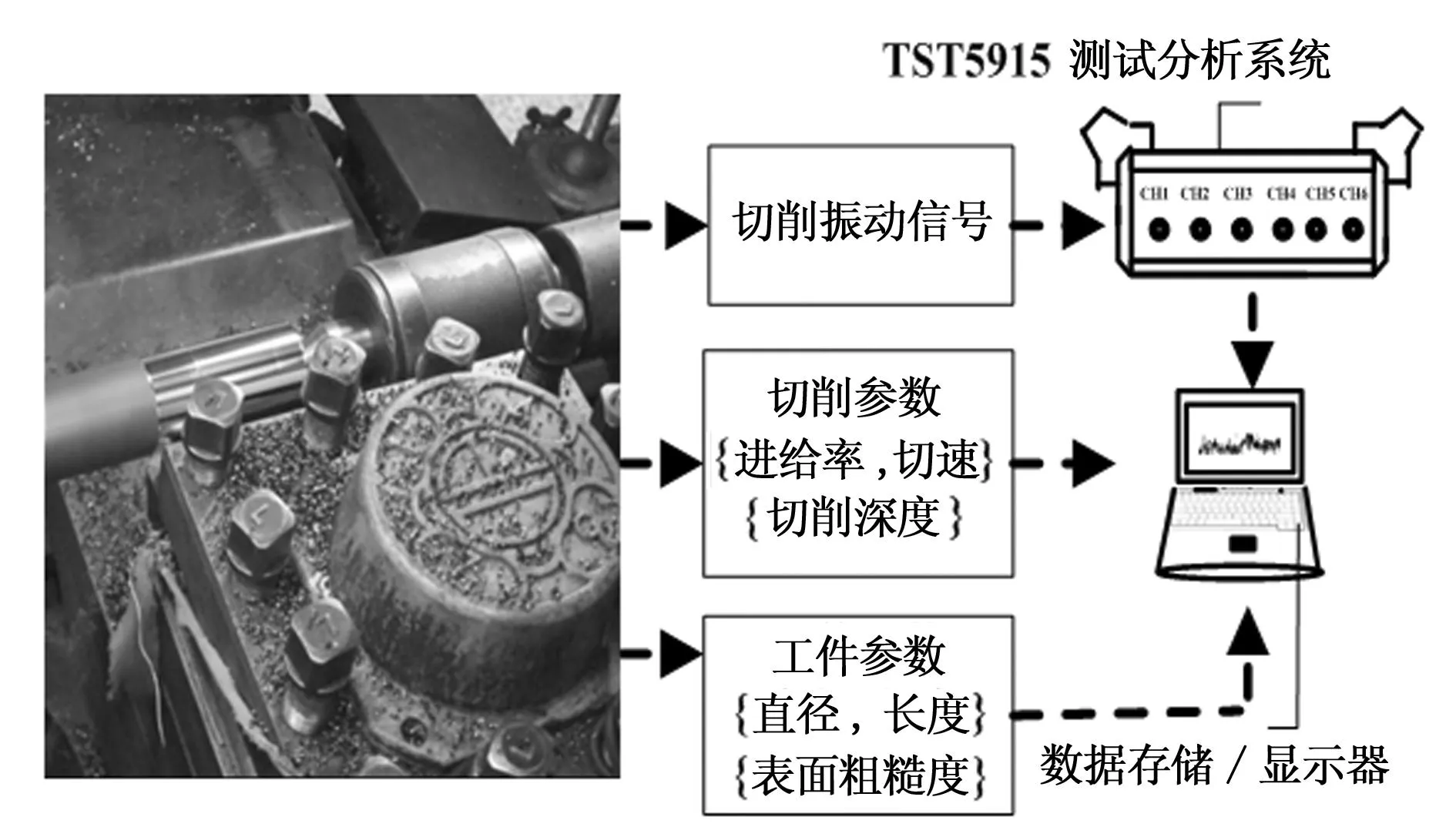
图3　实验装置简图

4实验研究

在数控车床CK6140上进行硬车削实验。实验装置简图如图3所示。试验所采用的工件材料为AISID2steel(淬火硬度55HRC和60HRC)和AISI4340steel(淬火硬度50HRC和55HRC)，刀具为日本住友电工CBN刀片(BNC160)。

采用3个PCB加速度传感器，测量刀具在3个方向上的振动信号，采样频率fs=20KHz。采用一个24位A/D多通道TST5915信号分析和测试系统进行信号采集，然后利用Matlab7.8软件进行信号处理。表1显示了其相应的质量特征。

依据SSA提取的融合特征Pe作为HMM的观察序列。为了减小观察值的规模，缩短训练时间，采用自组织特征映射神经网络(SOM)对特征矢量进行量化编码。利用表1中1～17样本，依据图2的策略进行模型训练。

图4和图5分别显示MoG_HMM和DHMM训练时EM误差迭代曲线。比较两图可知，MoG_HMM的训练速度要明显快于DHMM，这可能是由于图4训练数据的一致性要优于图5。但是，即使是在图5(训练步数40左右)的情况下，其训练时间也不会超过5s。由此可见，各个模型的学习速度是比较快的。

表1　切削参数及其相应的工件表面粗糙度

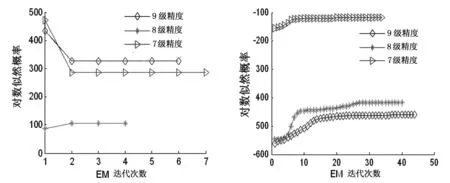
图4　MoG_HMM训练曲线　　　　　　　图5　DHMM训练曲线

当HMM训练完成以后,就可以采用图2的策略进行精度识别。图6和图7分别显示MoG_HMM和DHMM的工件表面粗糙度精度识别结果，由图可知，对于多数样本，HMM监测样本和实

图6　MoG_HMM的精度识别结果　　　　　　　　图7　DHMM的精度识别结果

际样本仍然在同一个精度范围内。比较两图可知，对于监测样本所在的精度区间，DHMM模型要比MoG_HMM模型具有较少的精度超差数，因而DHMM要比MoG_HMM具有较高的监测精度。同时采用χ比对的监测精度要明显高于概率比对的监测精度。虽然对DHMM的输入序列进行SOM编码有误差引入，但是这种类似聚类的方法在一定程度上缩小了相邻特征之间的相识度，增加了样本之间的类间距[11]，为此，样本更易于识别。

表2　工件表面粗糙度的精度等级识别率

同样的结论也能从表2的工件表面粗糙度精度等级识别率比较中得出，由表2可以看出，DHMM的精度等级识别率要高于MoG_HMM，对于7级精度样本，二者具有相同的识别率；但是，对于9级和8级精度样本，DHMM的精度等级识别率要明显高于MoG_HMM，为此，在对中、高精度的样本进行精度等级判别时，采用DHMM模型是比较合适的。另外，采用χ比对法能够明显提高这两种模型的精度等级识别率，但是，DHMM的监测精度要明显高于MoG_HMM的监测精度。

5结 论

(1)在分析了切削振动对工件表面形貌影响的基础上，提出了基于SSA的多通道融合特征提取方法，实验分析表明,所提取的融合特征Pe能够较好地用于工件表面粗糙度精度等级监测。

(2)无论是DHMM还是MoG_HMM，采用本文提出的χ比对法，对工件表面粗糙度精度等级识别精度要明显高于通常所采用的概率比对法；DHMM模型比MoG_HMM模型具有较高的工件表面粗糙度精度等级识别率。

参考文献：

[1]Salgado D,Alonso F A,Marcelo A,et al.In-process surface roughness prediction system using cutting vibrations in turning[J].The International Journal of Advanced Manufacturing Technology,2009,43(1/2):40-51

[2]Risbood K,Dixit U,Sahasrabudhe A.Prediction of surface roughness and dimensional deviation by measuring cutting forces and vibrations in turning process[J].Journal of Materials Processing Technology,2003,132(1):203-214

[3]Benardos P,Vosniakos G C.predicting surface roughness in machining:a review[J].International Journal of Machine Tools and Manufacture,2003,43(8): 833-844

[4]Zhong Z,Khoo L,HAN S.Prediction of surface roughness of turned surfaces using neural networks[J].The International Journal of Advanced Manufacturing Technology,2006,28(7/8):688-693

[5]Wang H,To S,Chan C,et al.A theoretical and experimental investigation of the tool-tip vibration and its influence upon surface Generation in single-point diamond turning[J].International Journal of Machine Tools and Manufacture,2010,50(3):241-252

[6]Hessainia Z,Belbah A,Yallese M A,et al.On the prediction of surface roughness in the hard turning based on cutting parameters and tool vibrations[J].Measurement,2013,46(5): 1671-1681

[7]Azizi M W,Belhadi S,Yallese M A,et al.Surface roughness and cutting forces modeling for optimization of machining condition in finish hard turning of AISI 52100 steel[J].Journal of Mechanical Science and Technology,2012,26(12):4105-4114

[8]Aouici H,Yallese M A,Chaoui K,et al.Analysis of surface roughness and cutting force components in hard turning with CBN tool:Prediction model and cutting conditions optimization[J].Measurement,2012,45(3):344-353

[9]Rabiner L R.A tutorial on hidden Markov models and selected applications in speech recognition[J].Proceedings of the IEEE,1989,77(2): 257-286

[10]Li X,Parizeau M,Plamondon R.Training hidden markov models with multiple observations-a combinatorial method[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(4):371-377

[11]Zhu K,Wong Y S,Hong G S.Multi-category micro-milling tool wear monitoring with continuous hidden Markov models[J].Mechanical Systems and Signal Processing,2009,23(2):547-560

(责任编辑：汪材印)

中图分类号：TG54

文献标识码：A

文章编号：1673-2006(2016)02-0107-05

作者简介：何康(1978-)，河南扶沟人，博士，主要研究方向：制造过程状态监测。

基金项目：国家自然科学基金资助项目(51075070),宿州学院校级科研平台项目(2014YKF15)。

收稿日期：2015-11-12

doi:10.3969/j.issn.1673-2006.2016.02.030