鄂尔多斯盆地红河油田裂缝识别

许君玉, 许新

(1.中国石油化工股份有限公司石油勘探开发研究院, 北京 100083; 2.北京市海淀区职业介绍服务中心, 北京 100195)

0 引 言

红河油田位于鄂尔多斯盆地天环坳陷南段,其东部临伊陕斜坡,西部接西缘冲断带,南部为渭北隆起。由于多期地质构造运动,区内形成了多条断裂和裂缝。裂缝是控制低渗透油气藏开发产能的关键性因素[1],裂缝的存在不仅改善了地层对流体的储集性能,而且作为渗流通道大大提高了低孔隙度低渗透率储集层的生产能力[2]。因此,对红河油田低孔隙度低渗透率储集层裂缝的研究意义重大。

1 裂缝特征

通过裂缝观察和对研究区21口取心井182条裂缝统计,裂缝岩性以砂岩为主,其含量大于90%;裂缝产状主要为高角度裂缝和垂直裂缝,占80%以上;裂缝开度范围0.1～0.3 mm;裂缝充填情况为未充填60%,其余为半充填和全充填各占一半,充填物主要是方解石和碳质泥屑。裂缝平均密度为0.25条/m,发育井段的垂直裂缝达到3～6条/m,水平裂缝密度相对较低,约为3条/m。

2 裂缝在测井曲线上的响应特征

裂缝在测井曲线上有2种响应特征。①低电阻率特征,即双感应、八侧向和阵列感应测井曲线均显示低电阻率值,八侧向与双感应电阻率值正异常;双井径微扩径,声波、中子值增大,密度值减小。②高电阻率特征,即双感应正异常显示高电阻率值,八侧向电阻率值在层的上部与双感应电阻率值正差异,在层的下部与双感应电阻率值负差异;声波、密度值减小,中子值增大。

3 裂缝识别方法

裂缝与基质的地质和地球物理特征差异性,地层中裂缝的存在会引起不同的测井响应,根据测井响应的不同变化,就可以识别和研究裂缝[3-18]。研究人员利用测井资料对裂缝进行了识别[19-21],但效果欠佳。在对红河油田裂缝识别的过程中,发现不同井的裂缝在测井曲线上的响应特征不同,因此利用测井曲线的响应特征识别裂缝比较困难。在对裂缝研究的基础上,利用常规测井曲线作为输入曲线的变尺度分形方法对红河油田裂缝进行了识别,与成像测井资料对比,效果较好。

3.1 变尺度裂缝识别方法

对裂缝识别的探索发现,在利用测井资料对裂缝进行识别的方法中,分形几何学的应用在研究储层的孔隙结构、储层的非均质性以及裂缝预测等方面取得了丰富的成果[22-23]。R/S分形(变尺度分形)技术是应用广泛且成熟的分形统计方法之一[24-26],方法中R为极差,它是最大累积离差与最小累积离差之差,代表了时间序列的复杂程度;S是标准差,它是变差的平方根,代表了时间序列的平均趋势,R/S之比代表无因次的时间序列的相对波动程度。对于一条对称的测井曲线z(i)(i=1,2,…,n),R和S的定义为

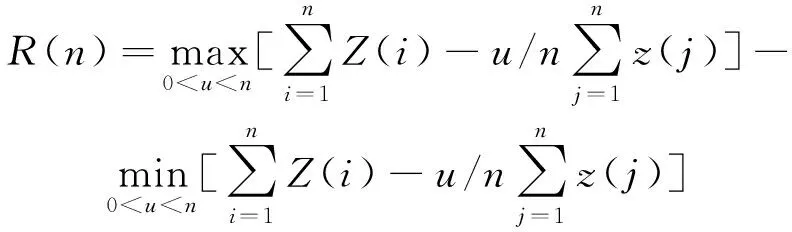
(1)

(2)

式中,n为逐点分析层段测井采样点数;u为由端点开始在0～n之间依次增加的采样点数;i和j为表示采样点个数的变量。

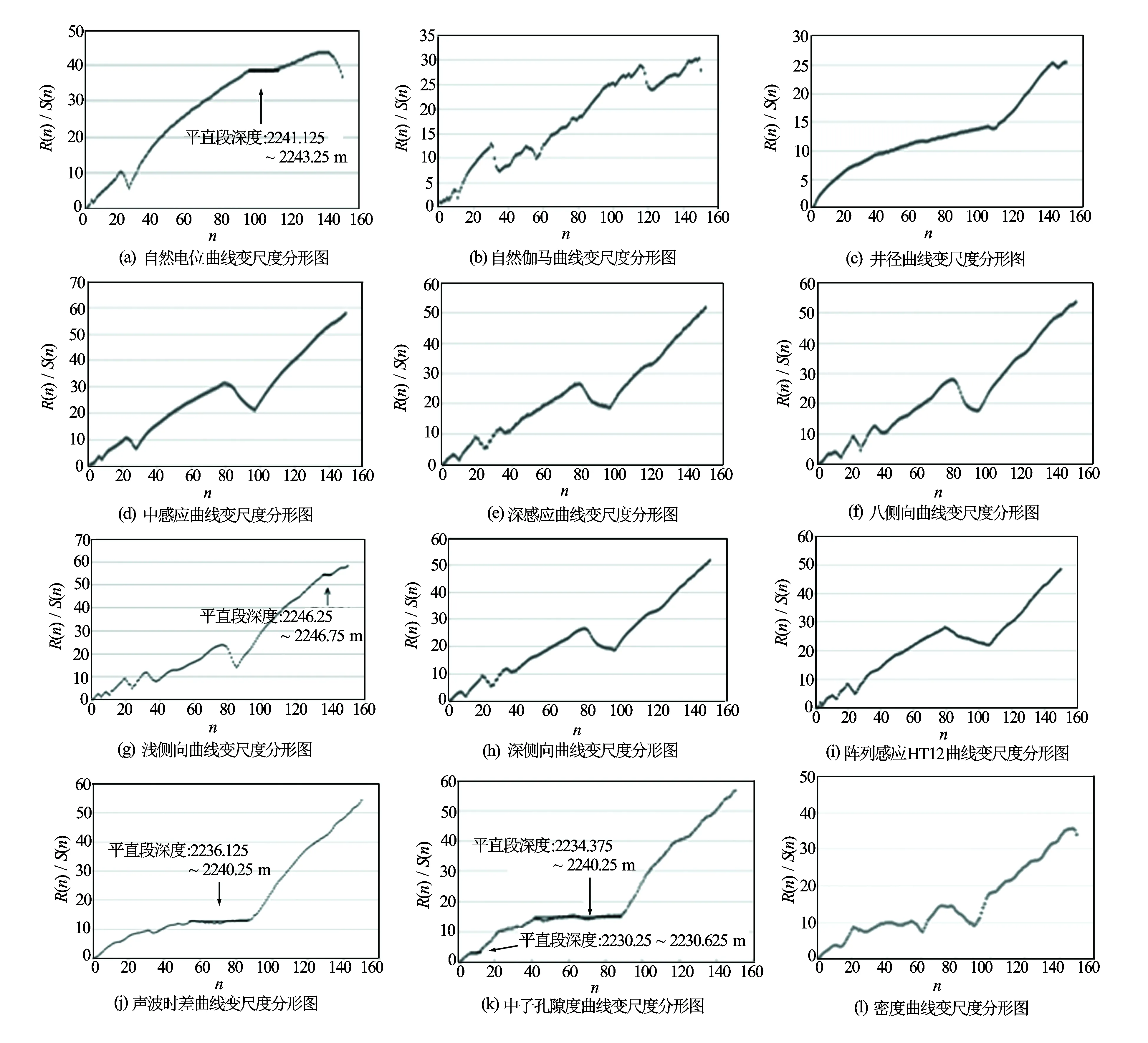
图1 HH1057-3井2 229～2 248 m井段不同测井曲线变尺度分形图

根据以上方法建立不同测井曲线的R(n)/S(n)与n的对应关系,与成像测井资料对比,可找出识别孔洞、裂缝最敏感的测井曲线。

图2 HH1057-3井裂缝在成像测井和R(n)/S(n)曲线上的响应特征

3.2 不同测井曲线对裂缝响应的敏感程度

用变尺度分形方法对红河油田研究区进行了裂缝识别。通过对不同测井曲线作变尺度R(n)/S(n)分形图与成像测井资料对比,发现不同测井曲线对裂缝识别的敏感程度不同。图1是对HH1057-3井在2 229～2 248 m井段用不同测井曲线的作的R(n)/S(n)的变尺度分形图。为避免岩性影响,在选取识别的裂缝井段时参照自然伽马、自然电位和井径测井曲线,选取岩性变化不大的井段作为裂缝识别井段。

从图1所作的各条测井曲线的变尺度分形图上看出,图1(a)、图1(b)和图1(c)的自然电位、自然伽马和井径这3条岩性测井曲线的变尺度分形图形态各不相同,只有自然电位曲线的变尺度分形图上2 241.125～2 243.25 m的井段为平直段,所以图1(b)和图1(c)的自然伽马和井径曲线对裂缝识别是不敏感的。图1(d)至图1(i)为电阻率曲线中感应、深感应、八侧向、浅侧向、深侧向和阵列感应测井曲线的变尺度分形图,这6条测井曲线的变尺度分形图形态相似,只在浅侧向曲线的变尺度分形图上2 246.25～2 246.75 m井段有一平直段,其余5条电阻率测井曲线变尺度分形图上均无平直井段,说明电阻率测井曲线中除浅侧向曲线外的其余曲线对裂缝识别不敏感。图1(j)、图1(k)和图1(l)的声波、中子孔隙度和密度3条孔隙度曲线的变尺度分形图中,前二者曲线形态相似,声波时差曲线的变尺度分形图上的平直段深度为2 236.125～2 240.25 m;中子孔隙度曲线的变尺度分形图上的平直段有2段,上段为2 230.25～2 230.625 m,下段为2 234.375～2 240.25 m;密度测井曲线变尺度分形图上没有平直段,说明密度测井曲线对裂缝识别不敏感。

图2左侧为HH1057-3井成像测井图识别的裂缝井段,识别出4段裂缝井段,第1段为2 230.30～2 230.80 m,第2段为2 233.38～2 236.20 m,第3段为2 237.00～2 239.10 m,第4段为2 239.80～2 242.12 m。图3右侧为自然电位、浅侧向、声波和中子孔隙度4条测井曲线所识别的裂缝井段与其左侧的成像测井图上识别的裂缝井段的对比。图2右侧自然电位曲线变尺度分形图上的直线段深度为2 241.125～2 243.25 m,顶部深度比成像测井图上的裂缝井段第4段底部深度浅0.995 m,与成像测井图上的裂缝井段重复率为12.86%,所以认为自然电位曲线变尺度分形法对裂缝识别不敏感。浅侧向曲线变尺度分形图上的直线段深度为2 246.25～2 246.75 m,在成像测井图上识别的所有裂缝井段的下方,与成像测井图上识别的裂缝井段没有重复,所以浅侧向曲线的变尺度分形法对裂缝识别不敏感。声波测井曲线变尺度分形图上的直线段深度2 236.125～2 240.25 m,其顶部深度比成像测井图上裂缝井段的第2段(2 233.38～2 236.20 m)底部深度浅0.075 m,底部深度比成像测井图上裂缝井段的第3段(2 237.00～2 239.10 m)底部深1.15 m,声波测井曲线变尺度分形法识别的裂缝井段与成像测井图上的裂缝井段重复率为43.5%。中子孔隙度测井曲线变尺度分形法识别出2段裂缝,上段(2 230.25～2 230.625 m)顶部深度比成像测井图上的裂缝井段第1段(2 230.30～2 230.80 m)顶部深度浅0.05 m,底部深度比成像测井图上裂缝井段第1段的底部深度浅0.175 m;下段(2 234.375～2 240.25 m)顶部深度比成像测井图上的裂缝井段第2段(2 233.38～2 236.20 m)顶部深度深0.995 m,底部深度比成像测井图上的裂缝井段第4段(2 239.80～2 242.12 m)底部深度浅1.87 m。中子

孔隙度测井曲线变尺度分形法识别的裂缝井段与成像测井图上的裂缝井段重复率为85.0%。所以,变尺度分形法识别裂缝中,中子孔隙度测井曲线是识别裂缝最敏感的曲线。

4 实际应用

用变尺度分形方法与常规测井曲线对裂缝的响应特征相结合对红河油田研究区内31口井进行了裂缝识别,裂缝识别率为80%以上。表1为有裂缝的岩心和成像测井裂缝井段与变尺度分形方法识别的裂缝井段顶、底深度对比。

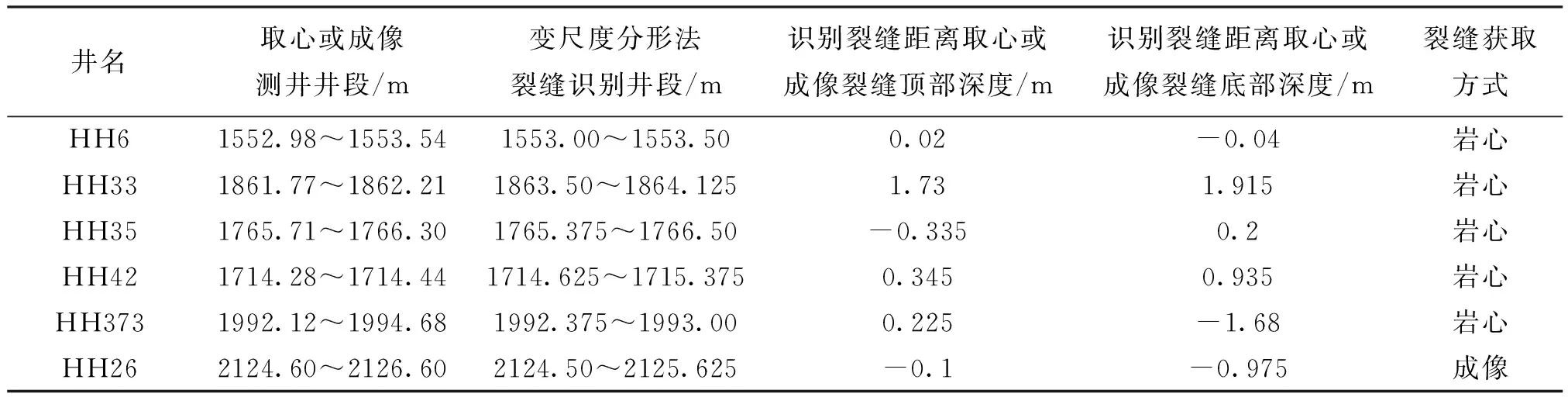
表1 红河油田取心井和成像测井裂缝井段与变尺度分形法识别裂缝井段对比表

表1(续)

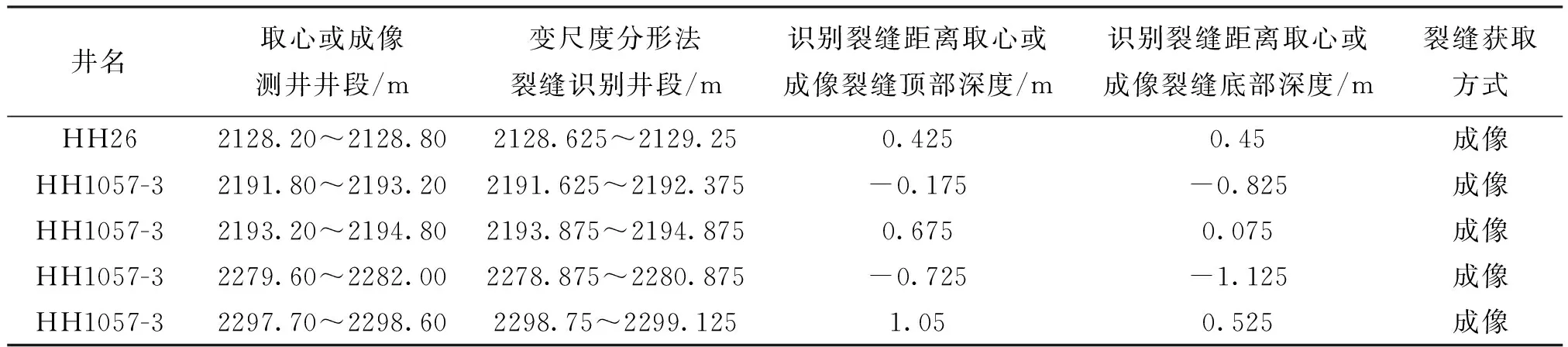
井名取心或成像测井井段/m变尺度分形法裂缝识别井段/m识别裂缝距离取心或成像裂缝顶部深度/m识别裂缝距离取心或成像裂缝底部深度/m裂缝获取方式HH262128.20～2128.802128.625～2129.250.4250.45成像HH1057-32191.80～2193.202191.625～2192.375-0.175-0.825成像HH1057-32193.20～2194.802193.875～2194.8750.6750.075成像HH1057-32279.60～2282.002278.875～2280.875-0.725-1.125成像HH1057-32297.70～2298.602298.75～2299.1251.050.525成像

用变尺度分形方法对红河油田研究区内试油资料中获得工业油流的井日产液量对比验证,按已有试油资料中日产液量由大到小排序,将识别的裂缝井列表于表2。由表2可知,日产液量大的井多数存在裂缝,说明了裂缝的存在对储层产量起着关键作用;另一方面,在识别的14口高产井中有11口井识别出了裂缝,说明了变尺度分形方法对裂缝识别的有效性。

表2 红河油田储层产液量与变尺度分形法识别裂缝

5 结 论

(1) 红河油田发育高角度裂缝和垂直裂缝。不同测井曲线对裂缝的测井响应特征不同,用常规测井曲线很难识别裂缝的存在。

(2) 裂缝在变尺度分形曲线上的响应特征表现为曲线偏离原来的变化趋势,成为近似一直线段。变尺度分形法裂缝识别中,不同测井曲线对裂缝响应的敏感程度不同,中子孔隙度测井曲线是识别裂缝最敏感的测井曲线,这种方法裂缝识别率较高。

(3) 变尺度分形方法识别裂缝操作简单、成本费用低,是识别裂缝较经济的方法。

(4) 利用变尺度分形方法识别的裂缝与岩心或成像测井识别的裂缝顶、底深度有一定的误差。因此,综合利用各种方法识别裂缝,才能最大限度地提高裂缝识别率。

参考文献:

[1] 徐朝晖, 徐怀民, 林军, 等. 常规测井资料识别砂砾岩储集层裂缝技术 [J]. 科技导报, 2008, 26(7): 34-37.

[2] 周灿灿, 杨春顶. 砂岩裂缝的成因及其常规测井资料综合识别技术研究 [J]. 石油地球物理勘探, 2003, 38(4): 425-430.

[3] 雍世和. 测井资料综合解释与数字处理 [M]. 北京: 石油工业出版社, 1999: 146-168.

[4] 叶涛, 蒋有录, 刘华, 等. 渤南洼陷裂缝成因类型及测井识别方法 [J]. 西安石油大学学报: 自然科学版, 2013, 28(1): 52-60.

[5] 王庆如, 李敬功. 碳酸盐岩气藏储量参数测井评价方法 [J]. 岩性油气藏, 2013, 25(6): 98-111.

[6] 王永刚. 济阳坳陷太古界变质岩储层裂缝识别与定量解释 [J]. 测井技术, 2012, 36(6): 590-595.

[7] 李健伟, 王磊, 陈利雯, 等. 碳酸盐岩储层裂缝识别技术研究 [J]. 工程地球物理学报, 2013, 10(6): 885-890.

[8] 姚胜林, 马玉甲. 碳酸盐岩储层裂缝识别技术研究 [J]. 工程地球物理学报, 2013, 10(6): 885-890.

[9] 蒲静, 秦启荣. 油气储层裂缝预测方法综述 [J]. 特种油气藏, 2008, 15(3): 9-13.

[10] 王珂, 张荣虎, 戴俊生, 等. 低渗透储层裂缝研究进展 [J]. 地球科学与环境学报, 2015, 37(2): 44-58.

[11] 吴琼, 林冬萍, 于春燕, 等. 新立油田低渗透油层裂缝测井识别方法 [J]. 大庆石油地质与开发, 2007, 26(2): 112-115.

[12] 邓少贵, 仝兆岐, 范宜仁, 等. 致密砂岩储集层裂缝的双侧向测井响应快速计算方法 [J]. 中国石油大学学报: 自然科学版, 2005, 29(3): 31-34.

[13] 柯式镇, 孙贵霞. 井壁电成像测井资料定量评价裂缝的研究 [J]. 测井技术, 2002, 26(2): 101-103.

[14] 肖承文, 朱筱敏, 李进福, 等. 高压低渗致密裂缝性砂岩测井评价技术 [J]. 新疆石油地质, 2007, 28(6): 761-763.

[15] 李军, 张超谟, 肖承文, 等. 库车地区砂岩裂缝测井定量评价方法及应用 [J]. 天然气工业, 2008, 28(10): 25-27.

[16] 郑军, 刘鸿博, 周文, 等. 阿曼五区块Daleel油田储层裂缝识别方法研究 [J]. 测井技术, 2010, 34(3): 251-256.

[17] 王瑞雪, 谈顺佳, 张晓峰. 常规测井方法在川西南地区储层裂缝识别中的应用 [J]. 石油地质与工程, 2014, 28(1): 41-43.

[18] 朱雷, 章成广, 居大海, 等. 利用声波全波列测井资料识别致密砂岩储层裂缝 [J]. 长江大学学报: 自科版, 2015, 12(8): 23-26.

[19] 王瑞雪, 张晓峰, 谈顺佳, 等. 基于成像测井资料多种滤波方法在裂缝识别中的应用 [J]. 测井技术, 2015, 39(2): 155-159.

[20] 赵杰, 李霞, 杨雪冰. 古龙地区青山口组泥岩裂缝有效储层识别方法 [J]. 大庆石油地质与开发, 2013, 32(4): 147-150.

[21] 杨雪, 王莹, 李万才. 应用常规测井资料进行裂缝识别 [J]. 吉林地质, 2013, 32(1): 102-105.

[22] 纪发华, 张一伟. 分形几何学在储层非均质性描述中的应用 [J]. 中国石油大学学报: 自然科学版, 1994, 18(5): 161-168.

[23] 王广才, 章成广, 居大海, 等. 分数维在识别深层致密砂岩裂缝中的应用 [J]. 长江大学学报: 自科版, 2015, 12(8): 33-36.

[24] 师光辉, 李永权, 王鲁. 结合变尺度分析方法和常规测井资料识别裂缝的发育 [J]. 石油仪器, 2013, 27(1): 49-51.

[25] 刘丽丽, 赵中平, 李亮, 等. 变尺度分形技术在裂缝预测和储层评价中的应用 [J]. 石油与天然气地质, 2008, 29(1): 31-37.

[26] 毛宁波.R/S分析估算储层参数分维研究新进展 [J]. 石油物探, 2000, 39(3): 108-126.