吉伯德-萨特思韦特防策略不可能性定理的逻辑初探
孙 雯,杜国平
(1.中国社会科学院 哲学研究所,北京 100732; 2.河北师范大学 马克思主义学院,石家庄 050024)
吉伯德-萨特思韦特防策略不可能性定理的逻辑初探
孙雯1,2,杜国平1
(1.中国社会科学院 哲学研究所,北京100732; 2.河北师范大学 马克思主义学院,石家庄050024)
摘要:自20世纪70年代吉伯德-萨特思韦特防策略不可能性定理确立后,引起了数学、经济学、计算机科学和哲学等诸多领域中学者的广泛关注。然而,在国内外文献中,对吉伯德-萨特思韦特防策略不可能性定理的逻辑研究还比较少。基于此,借助公理化的方法探讨吉伯德-萨特思韦特防策略不可能性定理,并形式化地给出定理的内容和证明,力图把精细的逻辑推理应用于复杂的过程分析中,使防策略投票这一过程形式化、清晰化,以期能指导人们进行合理、有效的决策活动。
关键词:吉伯德-萨特思韦特防策略不可能性定理;逻辑形式化;社会选择
一、对公平投票的质疑:吉伯德-萨特思韦特防策略不可能性定理
19世纪后期,投票选举理论的奠基人之一道奇森(Dodgson)就关注于对投票规则的研究,认为人们在投票时的行为更倾向于策略投票。在现代社会中,从村民自治选举到举国参与的总统选举,投票在社会生活中被广泛地应用。然而,在投票选举的过程中,用社会选择规则集结的个人偏好都是个人所表达出来的偏好,而不一定是其真实偏好。在正常情况下,个人的表达偏好与其真实偏好应该是一致的,但不排除在某些特殊情况下,个人出于某种目的而谎报自己的真实偏好,使决策结果发生有利于自己的变化,这就是所谓的“策略投票”。策略投票使得选举结果并不能体现人们的真实意愿,这严重影响了公众的权利。因此,防止策略投票操纵选举结果,也即“防策略”就显得尤为重要。从直观上讲,防止策略投票就是要求投票者不能从谎报他们的偏好中获益,进而可以抑制社会选择中的策略投票,促使投票者都投出自己的真实选票,从而使选举结果体现人们的真实意愿,以充分保障社会的公平和正义。
20世纪50年代,诺贝尔经济学奖得主肯尼斯·约瑟夫·阿罗(Kenneth J.Arrow)对投票选举方式做了更深入的研究,提出了著名的阿罗不可能性定理。阿罗将社会选择问题划归为寻找一个合理的将个人偏好聚合为集体选择的法则,也称之为社会福利函数。他指出,社会福利函数在满足一些合理性条件的前提下将不存在,这被称为“阿罗不可能定理”。具体来讲,社会福利函数应满足无限制定义域(unrestricted domain)、无关选项相独立(independence of irrelevant alternatives)、帕累托最优原则(Pareto principle)与无独裁者(Non-dictator)4个条件。但是,当有3个或更多候选人时,满足这些条件的任何理性群体决策将不存在。可见,随着候选人和投票者的增加,“程序民主”必将越来越远离“实质民主”。
在实际的社会选择中,个人的表达偏好常常与其真实偏好不一致,在有策略行为存在的情况下,再沿用阿罗不可能性定理的形式来描述社会选择问题显然已不准确。20世纪70年代,在阿罗定理的基础上,阿兰·吉伯德(Allan Gibbard)和马克·萨特思韦特(Mark Satterthwaite)提出了吉伯德-萨特思韦特(Gibbard-Satterthwaite)防策略投票不可能性定理,证明了当存在3个或更多候选人时,任何合理的投票系统都可以被操纵。换句话说,总是存在让投票者通过投出一个非真实意愿的选票而受益的可能。吉伯德-萨特思韦特防策略不可能性定理证明了策略投票的必然性,这在理论界引起了很大的震动,特别是对经济领域资源合理配置理论的存在性和合理性提出了巨大的挑战。
吉伯德-萨特思韦特防策略不可能性定理在西方经济学理论,特别是社会选择理论中有着十分重要的地位和意义。在过去的30年里,国外许多学者从经济学和数学的角度对吉伯德-萨特思韦特防策略不可能性定理进行分析,Gärdenfors[1]、Schmeidler、Sonnenschein[2]、Barberá[3]、Benoit[4]、Arunava Sen[5]和Tayor[6]都对这个定理进行过证明。本文使用逻辑形式化的方法来深入探讨吉伯德-萨特思韦特防策略不可能性定理,这对于读者理解定理的内容和证明,具有重要的意义。同时,对于国内哲学和逻辑工作者而言也有重要的参考价值。
二、吉伯德-萨特思韦特防策略不可能性定理的内容
首先,我们使用集合论和相关逻辑语言来描述吉伯德-萨特思韦特防策略投票不可能性定理的基本思想。
定义1.1集合A上的二元关系R:
自反性 —— ∀x∈A
xRx
非自反性 —— ∀x∈A
﹁(xRx)
对称性 —— ∀x,y∈A
如果xRy,那么yRx
非对称性 —— ∀x,y∈A
如果xRy,那么﹁(yRx)
反对称性 —— ∀x,y∈A
如果xRy并且yRx,那么x=y
传递性 —— ∀x,y,z∈A
如果xRy并且yRz,那么xRz
完全性 —— ∀x,y∈A
或者xRy或者yRx
定义1.2(弱序)如果R具有传递性和完全性,那么集合A上的二元关系R是一个弱序(weak ordering)。
定义1.3(线性序)如果具有传递性、完全性、反对称性,那么集合A上的二元关系R是一个线性序(linear ordering)。
如果R是A的一个弱序,那么R是完全的就表示R也是自返的。直觉上,一个弱序就表示有平局的情况,xRy可以解释为x至少像y一样好。一个线性序就没有平局的情况。xRy解释为或者x=y或者x优于y。
定义1.4R是A上的一个弱序,有偏好(strict preference)P和无差异(indifference)I, 即xPy⟺﹁(yRx),xIy⟺xRy∧yRx。Pi和Ii指第i个投票者的偏好和无差异性。如果R是A的一个弱序,那么关系I就表示相等,关系P就表示A的一个线性序。

如果P是一个(A,n)-断面,那么P可以写作〈P1,…,Rn〉,也可以表示为(≻1,…,≻n)。Ri(或≻i)是第i个投票者的选票,表示“投票者i想要的或喜爱的”。
定义1.6设A是一个非空集合,由A的所有子集组成的集合叫做A的幂集,记作ρ(A),即ρ(A)={x|x⊆A}。
P(A)是所有(A,n)-断面的集合,对于n∈Ν,函数V:P(A)→A是A的一个单值投票规则(resolutevotingrule)。函数V:P(A)→ρ+(A)是A的一个投票规则(votingrule)。函数V:P(A)→ρ+(A)→ρ+(A),且V(P)(v)⊆v,是A的一个社会选择函数(socialchoicefunction)。函数V:P(A)→ord(A),是A的一个社会福利函数(socialwelfarefunction)。
定义1.7(防策略)令P~iP′:表示P和P′仅在投票者i的选票中不同。如果P~iP′,则V(P)iV(P′),那么单值投票规则V是防策略(strategy-proof)或防操纵的(non-manipulable),简写为NM)。
定义1.8(非强加)如果∀a∈A∃P∶a∈V(P),那么投票规则V是非强加的(non-imposed,简记为NI)。这意味着任意候选人都可以成为获胜者。
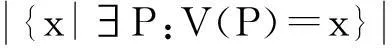
定义1.9(独裁的)如果存在某些k,使得V:P(A)→A,且映射任意P到≻k排序的顶端,那么单值投票规则V是独裁的(dictatorship)。
定义1.10(有效的)对于V和P,如果存在某些P′,具有P~iP′且V(P)≠V(P′),那么这个投票者i是有效的(effective)。
在上述准备的基础上,著名的“吉伯德-萨特思韦特防策略投票不可能性定理”可以表示为:
定理1.1(吉伯德-萨特思韦特防策略投票不可能性定理)
在线性投票的情况下,n是一个正整数,A是3个或3个以上候选人的集合,若对于(A,n)的任意单值投票规则是防策略(NM)的和非强加(NI)的,则必存在独裁[7]。
三、吉伯德-萨特思韦特防策略不可能性定理的证明
吉伯德-萨特思韦特防策略投票不可能性定理是社会选择理论和实施理论中具有标志性的成果,是防策略投票理论的基石。吉伯德-萨特思韦特防策略投票不可能性定理也是比较复杂的,因此它的证明显得尤为重要。吉伯德-萨特思韦特防策略投票不可能性定理有很多证明方法,Saari方法是目前较新的方法,该证明不仅在数学上十分完美,而且在经济学与社会选择理论上更有意义[8]。下面将在第一部分工作的基础上,运用逻辑形式化的证明方法给出吉伯德-萨特思韦特防策略投票不可能性定理证明的基本思路。


引理2.1(过渡引理)如果V是NM,那么V有CP。

引理2.2(有效引理)如果V是NM并且NI,i对于P是有效的,那么在P中,V(P)是i-选票的顶端。
证明:假设V是NM并且NI,那么通过过渡引理,V有CP。
假定对于P来说,i有效。那么V(P)ix,其中x是在P中i投票的顶端。
因为i是有效的,存在意向表P′,其中P~iP′并且V(P)≠V(P′)。由NM,得到V(P)iV(P′)。


我们也可以这样看,在Q中,i最喜欢的候选人是x。现在令所有其他投票者改变他们的投票,依次地,通过向上移动x,不改变y和z的顺序。那么通过NI,存在j,R,R1,有R≈jR1,V(R)=V(Q)=y,并且V(R1)=x。
假定i在R中无效,在R中,令R′是改变i-选票从xyz到xzy的结果。在Q中,令Q′是改变i-选票从xyz到xzy的结果。那么V(Q′)=z,V(R′)=y。这与CP矛盾。对于R′可以通过毗邻换位改变选票到达Q′,并且不影响y和z的相关顺序,所以i在R中是有效的。


可见,在这两个示例中,下面的一行都和CP有矛盾:通过向左移动,i可以操纵下行右边的选票。得证。
定理1.1 (吉伯德-萨特思韦特防策略投票不可能性定理)在线性投票的情况下,n是一个正整数,A是3个或3个以上候选人的集合,若对于(A,n)的任意单值投票规则是防策略(NM)的和非强加(NI)的,则必存在独裁[7]。
证明:令V是一个单值投票规则,并且是NM和NI,通过NI,使得i对于P是有效的。假设存在另一个对于P的有效投票者j。通过有效引理,对于每个P′,P~iP′,i决定投票。并且对于每个P″,P~jP″,j决定投票。
令Q是i和j改变他们选票的结果,i对应它的选票P′,j对应它的选票P″。那么,如下所示:

假定V(Q)≠V(P′),那么在P′中,j是有效的。通过有效引理,在P′中,V(P′)应该等价于j的偏爱,但是并非如此。因此V(Q)=V(P′)。相似地,在P″中,i是有效的。通过有效引理,在P″中,V(P″)应该等价于i的偏爱,但是并非如此。矛盾。
对于P来说,i是唯一有效的投票者。令R是任意的意向表,R0是所有投票者的结果,除了i改变他们的选票P为选票R,这个投票并没有改变,并且在R0中,i仍是唯一的有效投票者。从而得到,在R中,i决定投票的结果。所以,对于任意的意向表,i是唯一有效的投票者,因此,i是独裁者。
四、结语
通过逻辑形式化的方法,来刻画吉伯德-萨特思韦特防策略投票不可能性定理,这对于读者认识和理解社会选择中的策略投票提供了一个十分重要的分析视角。更富有启发性的是,将社会选择理论中的吉伯德-萨特思韦特防策略投票不可能性定理,转化为一个纯形式化的表达,构建了和自动推理的联系,以期最终实现定理的机器自动证明,这也是逻辑作为工具应用到社会选择中的重要价值。另一方面,吉伯德-萨特思韦特防策略不可能性定理中存在着很多精细的问题,它们为逻辑提供了一个很好的直观来源和分析舞台。对此,目前国外学者的更进一步的想法是采用更具表达力的形式化工具,来进一步形式化投票变化过程,以展示某些情境下的精细结构。可见,社会选择中的投票互动及其变化的复杂性反过来又可以为形式化本身的研究提供思想源泉,从而激发逻辑的进一步发展,促其产生新的逻辑分支和分析工具。因此,从一个学科的角度去研究另一个学科的理论,用一个学科中的方法来研究另一个学科中的问题,最终完美地刻画和解决策略投票问题,这在今天具有重要的理论意义和现实意义。
参考文献:
[1]GRDENFORSP.Aconciseproofoftheoremonmanipulationofsocialchoicefunctions[J].Publicchoice,1977,32:137-142.
[2]SCHMEIDLERD,SONNENSCHEINH.Twoproofsofthegibbard-satterthwaitetheoremonthepossibilityofastrategy-proofsocialchoicefunction[J].Decisiontheoryandsocialethicstheoryanddecisionlibrary,1978,17:227-234.
[3]BARBERS.Strategy-proofnessandpivotalvoters:adirectproofofthegibbard-satterthwaitetheorem[J].Internationaleconomicreview,1983,24(2):413-417.
[4]BENOITJ.Thegibbard-satterthwaitetheorem:asimpleproof[J].Economicletters,2000,69:319-322.
[5]SENA.Anotherdirectproofofthegibbard-satterthwaitetheorem[J].Economicletters,2001,70(3):81-385.
[6]TAYLORAD.Themanipulabilityofvotingsystems[J].TheAmericanmathematicalmonthly,2002,109(4):321-337.
[7]TAYLORAD.Socialchoiceandthemathematicsofmanipulation[M].Cambridge:Cambridgeuniversitypress,2005:61.
[8]VANEIJCKJ.Ageometriclookatmanipulation[M].Computationallogicinmulti-agentsystems,lecturenotesinartificialintelligence,editedbyJ.Leiteetal,2011:92-104.
(责任编辑张佑法)
Preliminary Study on Logic of Gibbard-Satterthwaite Strategy-Proof Impossibility Theorem
SUN Wen1, 2, DU Guo-ping1
(1.Institute of Philosophy, Chinese Academy of Social Sciences, Beijing 100732, China;2.College of Marxism, Hebei Normal University, Shijiazhuang 050024, China)
Abstract:Since Gibbard-Satterthwaite strategy-proof impossibility theorem was established in the 1970s, it has drawn the widespread attention of scholars in fields of mathematics, economics, computer science and philosophy. However, it is seldom found the research on logics of the Gibbard-Satterthwaite theorem. This paper discussed Gibbard-Satterthwaite strategy-proof impossibility theorem with the axiomatic method, and elaborated the content and proving process of this theorem formally. It is trying to apply the fine logical reasoning to the complex processes analysis to make the strategy-proof voting process more formal and clear, hoping to guide people to make rational and effective decision-making activities.
Key words:Gibbard-Satterthwaite strategy-proofness impossibility theorem; logic formalization; social choice
中图分类号:B81
文献标识码:A
文章编号:1674-8425(2016)03-0013-05
作者简介:孙雯(1982—),女,河北石家庄人,河北师范大学马克思主义学院讲师,哲学博士,中国社会科学院哲学研究所博士后,研究方向:现代逻辑。
基金项目:国家社会科学基金重大项目“应用逻辑与逻辑应用研究”(14ZDB014);河北师范大学人文社会科学基金项目“基于多主体策略逻辑的防操纵研究”(S2014809)
收稿日期:2015-10-09
doi:10.3969/j.issn.1674-8425(s).2016.03.003
引用格式:孙雯,杜国平.吉伯德-萨特思韦特防策略不可能性定理的逻辑初探[J].重庆理工大学学报(社会科学),2016(3):13-17.
Citation format:SUN Wen, DU Guo-ping.Preliminary Study on Logic of Gibbard-Satterthwaite Strategy-Proof Impossibility Theorem[J].Journal of Chongqing University of Technology(Social Science),2016(3):13-17.

